自由运行结构动态载荷识别的格林函数法
2016-10-19彭凡马庆镇肖健韦冰峰刘杰
彭凡马庆镇肖健韦冰峰刘杰
(1.湖南大学机械与运载工程学院,长沙 100190)(2.北京强度与环境研究所,北京 100076)
自由运行结构动态载荷识别的格林函数法
彭凡1马庆镇1肖健2韦冰峰2刘杰1
(1.湖南大学机械与运载工程学院,长沙 100190)(2.北京强度与环境研究所,北京 100076)
将Green函数法应用于平动自由结构的载荷识别问题.不计刚-柔耦合效应,建立测点的绝对运动加速度和动态激励的卷积关系,Green核函数由整体刚体运动与弹性振动的脉冲响应迭加而成,采用正则化方法求解反卷积问题.对自由梁和组合薄壁结构给出两个算例,以数值仿真结果叠加20%噪声水平的随机噪声模拟实测响应,结果表明,Green函数法能有效地反演复杂平动自由结构的动载荷,正则化方法求解此类问题的稳健性和耐噪性强.文中得到的Green函数法对复杂自由结构体系的动载荷反演具有应用潜力.
整体平动,自由结构,载荷识别,格林函数,正则化
引言
自由结构载荷的时域识别技术在航空航天工程领域有重要的应用价值,如通过飞行试验所积累的有关力学环境的遥测数据估计飞行器飞行过程中所承受的外载荷,或者基于少量实测数据预示整个飞行器的动力学响应,这对运载工具和飞行器结构的优化设计是极其必要的.目前,人们已发展了较多的载荷时域识别方法.其中一类是通过模态叠加将问题变换到模态空间中反求模态力[1-5];另一类应用较广泛的方法是基于线性叠加原理将响应与动态力的关系通过卷积表示[6],求解卷积方程得到动载荷的时间历程,Doyle[7]结合小波变换与傅里叶变换的反卷积方法实现载荷重构.Liu与Han[8]对复合材料层合板施加Green脉冲载荷函数与Heaviside阶跃载荷函数,由动力学响应确定卷积中的核函数;韩旭和刘杰等[9,10]基于正则化方法求解数值离散后的反卷积方程,分析多源动态载荷反求问题;王晓军、杨海峰和邱志平等[11]基于Green函数方法研究动态载荷的区间识别方法.对自由结构,其运动耦合了整体刚体运动,人们也发展了一些特殊的方法来识别动载荷,Kreitinger和Luo[12]提出了计权加速度法(SWAT),利用测量的加速度值乘以计权系数得到动态载荷的等效合力,关键是难以确定计权系数;朱斯岩与朱礼文[13]将模态矢量按测点自由度归一化,构造运载火箭动态载荷的识别方法;毛玉明和郭杏林等[14]通过模态叠加法,将弹性模态与整体刚体运动分离,在弹性振动的状态空间中建立反求模型,得到自由-自由运行结构体系的载荷.本文将Green函数法应用于具有整体刚体平动的自由结构载荷识别问题,考虑到加速度是容易测到的响应信号,为此,本文的工作侧重于基于测点的绝对运动加速度反求动载荷,为自由运行的复杂结构体系发展不同的载荷反演途径.
1 响应与激励的卷积关系及其离散
假设结构的动力学特性是线性时不变的,忽略刚-柔耦合效应,整体刚体平动自由结构的动力学方程表示为

式中M、C和K分别为质量、阻尼与刚度矩阵.将系统的绝对运动分解为整体刚体运动和弹性振动运动之和,即

式中下标“R”和“E”分别表示刚体运动和弹性振动.由模态叠加法求解式(1),令

式中ΦR是整体刚体运动模态矩阵;ΦE是弹性振动模态矩阵;qR和qE分别是整体刚体运动和弹性运动的模态坐标.结合式(3)和式(1),得到式中ωi和ξi分别为弹性振动的各阶频率和模态阻尼比;QE和QR分别为弹性振动模态力与整体刚体运动模态力,且有QE=(ΦE)TP,QR=(ΦR)TP.

将结构所受任意动态载荷历程在时域内表示为

式中Dirac函数Δ表示作用于结构的单位冲激载荷.由式(4)可直接导出单位冲激函数产生的弹性振动和整体运动的模态加速度脉冲响应,即载荷作用点到加速度响应测点的Green函数.考虑零初始条件,且设初瞬时,载荷值等于零,则依线性叠加原理得到测点的绝对加速度响应与激励的卷积关系

式中x表示载荷作用点;gE(x,t)和gR(x,t)分别是弹性振动和整体刚体运动的Green核函数.
在时间域内用m个等间隔的采样点进行离散,令Δt为离散的采样时间间隔,i和Fi是t=iΔt时的加速度和待反求的载荷值,式(6)可离散为如下形式


式中G为Green核函数矩阵.
当结构受到多个载荷作用时,系统总的绝对加速度响应是各载荷引起的加速度响应的线性叠加,故可将多源载荷问题表示为式(8)所示形式[9].
2 反问题求解的正则化方法
计入响应数据中的误差或噪声,式(8)改写成如下形式

对核函数矩阵G作奇异值分解,有

式中σi(i=1,2,…,m)为奇异值,U=(u1,u2,…,um)和V=(v1,v2,…,vm)分别是左奇异值和右奇异值向量矩阵,并满足UTU=VTV=I,其中I是单位矩阵.设矩阵G可逆,由式(7)得估计的动态外载荷Fδ为

式(11)表明,动态外载荷的估计值 Fδ与真实值之间的误差主要是由于两个因素导致的,一是测量响应数据中不可避免的噪声,二是系统固有的核函数矩阵的小奇异值.
本文采用正则化方法反求式(8),引入正则化算子f(α,σi),当小奇异值σi趋于零,f(α,σi)/σi也趋于零,由此可得到实际载荷的一个稳定的近似估计
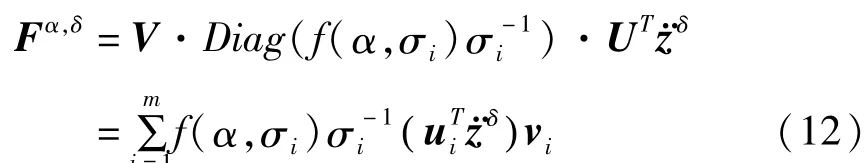
式中α是正则化参数.若取正则化算子

得到截断奇异值分解(TSVD)算法[15].采用广义交叉验证准则(GCV)[16]得到α,构造如下函数

3 算例分析
首先考虑一自由梁,取自文献[13]给出的飞行器简化模型,由一个长50 m、直径为3 m、壁厚为0. 005 m的铝质圆筒构成.如图1所示,其有限元模型共有101个节点,100个单元,在各个节点上加1600 kg的等效集中质量.在底部节点1作用轴向载荷F (t)=1.7×106(1-e-5t)+5×104sin(10πt).

图1 自由运行飞行器简化模型Fig.1 Simplified model of space vehicle in unconstrained state
以节点40的响应作为反求输入,首先在载荷作用点1施加单位冲激脉冲力,计算40节点的绝对加速度响应,由此确定Green函数.然后,进行F(t)作用下的正问题计算,得到40节点的绝对加速度响应,将其迭加噪声水平为20%的随机噪声来模拟实验测量的响应,带噪的加速度响应可用下式表示

图2 节点40的绝对加速度响应历程Fig.2 The response history of absolute acceleration for node 40
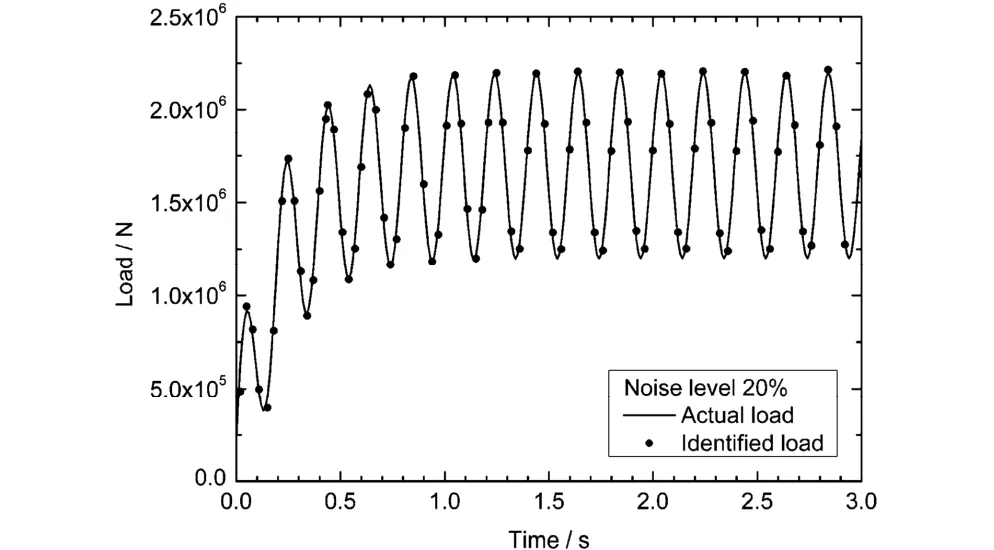
图3 自由梁的实际载荷与识别出的载荷Fig.3 The actual load and identified load on free beam
从图中可见,反演出的载荷与实际载荷吻合较好.再考虑图4(a)所示某复杂组合结构,由联接于底部的内外加筋薄壁构件组成,其中,内部结构包含薄壁圆筒、纵向和横向隔板.在底圈受轴向力作用,结构发生沿z向的整体平动和较强烈的结构振动.对组合结构用板壳单元和梁单元划分有限元网格,如图4(b)所示,其中,底圈上的节点均匀分布.在底圈各节点上施加均匀的半正弦冲击力F (t),冲击时间为50 ms,幅值为1000 N.以图4(a)所示的内部结构纵向板中部的节点A为反求的输入点.统一取0.03的模态阻尼比,与前面算例的过程类似,模拟实验测量的加速度响应示于图5.反演出的载荷由图6给出.可见,反求结果与实际载荷吻合较好.

图4 组合薄壁结构与分析模型Fig.4 Composite thin-walled structure and its analysismodel
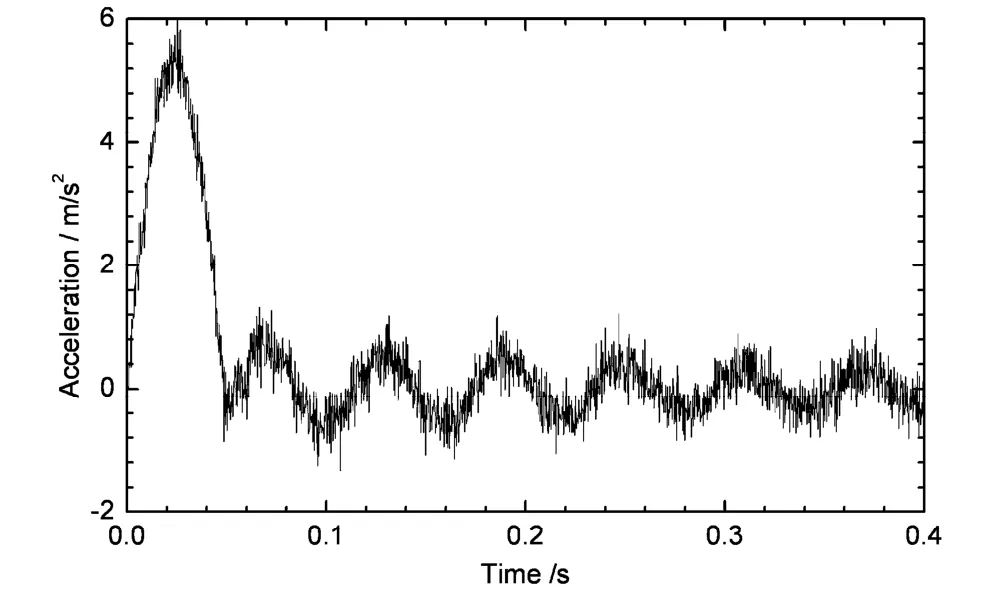
图5 节点A的绝对加速度响应历程Fig.5 The response history of absolute acceleration for node A

图6 组合薄壁结构的实际载荷与识别出的载荷Fig.6 The actual load and identified load on composite thin-walled structure
综合两个算例的分析结果可见,虽然计入了较高水平的随机噪声,载荷反演仍然保持了良好的精度.进一步的数值实验表明,将反求输入测点选在沿z向局部刚度较大的部位,有望提高动载荷反演的稳健性.这些特征提示,由于耦合了整体运动,核函数矩阵的病态性得到了一定改善,在局部刚度较大的部位,整体运动的加速度占绝对运动加速度的比例高,由此使得正则化方法的稳健性和耐噪性得到提高.
4 结论
将Green核函数耦合整体刚体运动与弹性振动的脉冲响应,结合正则化求解,以测点的绝对运动加速度响应为输入反演整体平动自由结构的动载荷,数值仿真算例验证了方法的有效性,反求结果的精度较高.数值试验结果也提示,整体刚体运动的引入降低了反求问题的病态性.选取局部刚性较大的测点位置,有望提高正则化方法的稳健性和耐噪性,以克服实际应用中加速度信号易受噪声污染这一问题.总之,基于绝对加速度反求的Green函数法对复杂的自由运行结构体系的动载荷反求问题具有明显的应用潜力.
1 朱继梅,吕忠达.连续系统动态载荷识别的时域方法.振动工程学报,1989,2(3):10~19(Zhu JM,Lu Z D. Time domain identification method of dynamical loads on a continous system.Journal of Vibration Engineering,1989,2(3):10~19(in Chinese))
2 时战,许士斌,初良成,等.利用脉冲响应函数识别载荷的时序法.振动工程学报,1995,8(3):235~242(Shi Z,Xu SB,Chu LC,etal.Time series analysis for load identification by using impulse response function.Journal of Vibration Engineering,1995,8(3):235~242(in Chinese))
3 张运良,林皋,王永学,等.一种改进的动态载荷时域识别方法.计算力学学报,2004,21(2):209~215(Zhang Y L,Lin G,Wang Y X,etal.An improvedmethod of dynamic load identification in time domain.Chinese Journal of Computational Mechanics,2004,21(2):209~215(in Chinese))
4 蔡元奇,朱以文.基于逆向滤波器的动态载荷识别方法.振动工程学报,2006,19(2):200~205(Cai Y Q,Zhu Y W.Time domain identification method for dynamic loads based on inverse direction filter.Journal of Vibration Engineering,2006,19(2):200~205(in Chinese))
5 张方,朱德懋,张福祥.动载荷识别的时间有限元模型理论及其应用.振动与冲击,1998,17(12):1~5(Zhang F,Zhu D M,Zhang F X.The theory and application of time elementmodel for dynamic load identification.Journal of Vibration and Shock,1998,17(2):1~5(in Chinese))
6 Inoue H,Harrigan JJ,Reid SR.Review of inverse analysis for indirectmeasurement of impact force.Applied Mechanics Review,2001,54(6):503~525
7 Doyle JF.A wavelet deconcolutionmethod for impact force identification.Experimental Mechanics,1997,37(4):404 ~408
8 Liu G R,MaW B,Han X.An inverse procedure for identification of loads on composite laminates.Composites Part B:Engineering,2002,33(6):425~432
9 韩旭,刘杰,李伟杰,赵卓群.时域内多源动态载荷的一种计算反求技术.力学学报,2009,41(4):595~602 (Han X,Liu J,LiW J,Zhao Z Q.A computational inverse technique for reconstruction of multisource loads in time domain.Chinese Journal of Theoretical and Applied Mechanics,2009,41(4):595~602(in Chinese))
10 Sun X S,Liu J,Han X,et al.A new improved regularization method for dynamic load identification.Inverse Problems in Science and Eengineering,2014,22(7):1062 ~1076
11 王晓军,杨海峰,邱志平,张红.基于Green核函数的动态载荷区间识别方法研究.固体力学学报,2011,32 (1):95~101(Wang X J,Yang H F,Qiu Z P,Zhang H.Research on interval identificationmethod for dynamic loads based on Green′s function.Chinese Journal of Solid Mechanics,2011,32(1):95~101(in Chinese))
12 Kreitinger T,Luo H L.Force identification from structural response.In:Proceedings of the 1987 Sem Spring Conference on Experimental Mechanics,Houston,1987:851~855
13 朱斯岩,朱礼文.运载火箭动态载荷识别研究.振动工程学报,2008,21(2):135~139(Zhu SY,Zhu LW. Dynamic load identification on lunch vehicle.Journal of Vibration Engineering,2008,21(2):135~139(in Chinese))
14 毛玉明,郭杏林,赵岩,朱礼文,潘忠文.自由-自由运行体系动态载荷反演问题研究.计算力学学报,2010,27 (1):35~39(Mao Y M,Guo X L,Zhao Y,Zhu LW,Pan ZW.Study of dynamic force identification for freefree structural system.Chinese Journal of ComputationalMechanics,2010,27(1):35~39(in Chinese))
15 Hansen PC.Truncated SVD solutions to discrete ill-posed problemswith ill-determined numerical rank.SIAM Journal on Scientific and Statistical Computing,1990,11(3):503~518
16 Golub G H,Heath M,Wahba G.Generalized cross-validation as a method for choosing a good ridge parameter. Technometrics,1979,21(2):215~223
GREEN KERNEL FUNCTION APPROACH OF LOAD IDENTIFICATION FOR FREE STRUCTURESW ITH OVERALL TRANSLATION
Peng Fan1Ma Qingzhen1Xiao Jian2Wei Bingfeng2Liu Jie1
(1.College of Mechanical and Vehicle Engineering,Hunan University,Changsha 410082,China)(2.Research Institute of Beijing Structure and Environment Engineering,Beijing 100076,China)
Green function method was extended to dealwith the load identification of free structureswith overall translation.The kernel function was obtained by the superposition of impulse response of overall translation and elastic vibration without taking into account rigid-flexible coupling effect,the convolution integral relationship of absolutemotion acceleration atmeasuring point and dynamic loads was constructed,and the regularization algorithm of truncated singular value decomposition(TSVD)was applied to solve the corresponding de-convolution equations.The proposedmethod was used to analyze a beam and a composite thin-walled structure in themotion of overall translation.The numerical simulation data was superimposed with random noise of 20%noise level and taken as the input of inverse problem to identify the given dynamic load.It is shown thatGreen function approach described in the paper can be effectively used to identify the dynamic loads acting on complex structures of overall translation,and regularization algorithms can solve this type of inverse problems with high robustness and noise resistance.
overall translation,free structure,load identification,Green function,regularization
11 April 2014,revised 01 July 2014.
E-mail:fanpeng@hnu.edu.cn
10.6052/1672-6553-2015-057
2014-04-11收到第1稿,2004-07-01收到修改稿.
E-mail:fanpeng@hnu.edu.cn
