基于SKA1-low的数字波束形成技术*
2016-10-19劳保强郭绍光魏延恒伍筱聪
劳保强**,安 涛,郭绍光,魏延恒,陆 扬,伍筱聪
(中国科学院 上海天文台,上海 20030)
PENG Bo,JIN Chengjin,DU Biao,et al.China's participation in the SKA the world's largest synthesis radio telescope[J].Scientia Sinica:Pysica,Mechanica & Astronomica,2012,42(12):1292-1307.(in Chinese)
基于SKA1-low的数字波束形成技术*
劳保强**,安涛,郭绍光,魏延恒,陆扬,伍筱聪
(中国科学院 上海天文台,上海 20030)
为配合我国参与平方公里射电阵(SKA)项目,深入理解数字波束形成条件下的射电干涉观测和相应数据处理算法,提出了基于多相滤波器组信道化数字移相波束形成和基于分数阶时延滤波器数字波束形成两个技术算法,前者使用互相关法求解相移量来提高波束指向精度,后者是传统算法与射电观测理论的有效结合。首先,详细介绍了算法的理论推导并分析了它们的优缺点;然后,通过仿真实验验证了这两个算法的正确性,仿真结果表明基于多相滤波器组信道化数字移相波束形成算法相比传统算法具有一定的优越性;最后,分析了不同阶数时延滤波器对波束形成的影响并得出了相应结论。这些仿真结果及结论可为从事SKA项目的科研人员提供参考。
平方公里射电阵项目;低频阵列;数字波束形成;多相滤波器;分数时延
1 引 言
国际大科学工程——平方公里射电阵(Square Kilometre Array,SKA)是由全球超过10个国家计划合资建造的世界最大综合孔径射电望远镜[1],将建于澳大利亚、南非及南部非洲8个国家的无线电宁静区域,由分布在3 000 km范围内的约2 500面15 m口径碟型天线、250个直径约60 m的致密孔径阵列,以及100万个偶极子组成的稀疏孔径阵列组成,其接收面积约1 km2,频率覆盖范围50 MHz~20 GHz。SKA科学涉及宇宙的早期演化、各级天体(星系、恒星、行星)的诞生和演化、引力波探测、引力理论检验、宇宙磁场的起源和演化、地外文明搜寻等各方面,将为人类认识宇宙提供重大机遇。SKA由于规模巨大,所以分为SKA1和SKA2两个阶段完成,SKA1建设阶段时间为2018~2023年,SKA1阶段将在澳大利亚建设约131 072个对数周期双极化天线组成的低频综合孔径阵列(SKA1-low),在南非建设133面15 m口径以及64面13.5 m口径的蝶形天线组成的中频阵列(SKA1-mid)。
SKA1-low系统又分为3个子系统,分别是台站系统、中央信号处理子系统(Central Signal Processor,CSP)和科学数据处理子系统(Science Data Processor,SDP)。其中,台站系统中比较重要的环节是波束形成,它对后续的各个处理环节均有影响。例如CSP中的数据相关处理部分,输入的数据是波束形成数据,波束形成的质量将会影响CSP输出数据的正确性乃至影响到最终图像的动态范围[2]。
目前,在低频射电频段世界上主要的在运行观测设备包括欧洲的低频阵列(Low Frequency Array,LOFAR)[3]、澳大利亚的默奇森宽视场阵列(Murc- hison Widefield Array,MWA)[4],以及我国自主研发的台址位于新疆天山的21 cm阵(21cm Array,21CMA)望远镜。这些低频阵列的特点是天线固定不动、视场大,观测指向由波束形成器来控制。波束形成按照实现方式的不同分为模拟波束形成和数字波束形成两大类。模拟波束形成相对于数字波束形成成本低,功耗小,但是硬件结构复杂,精度不高。随着数字技术的发展,模拟波束形成器有被数字波束形成器逐渐取代趋势[5]。目前,LOFAR采用了数字波束形成技术[6],而MWA[7]和21CMA也正考虑由模拟波束合成向数字波束形成升级。21CMA是我国自行研制的工作在低频射电频段的干涉阵,也是国际上建设最早的SKA探路者项目。21CMA目前采用的是基于固定电缆长度的相位调整和波束形成技术。尽管国际上SKA先导设备已经开展了数字波束形成的实验,但我国尚无采用数字波束形成技术开展干涉观测的先例,这一空白亟待填补。由于这一空缺,使得低频干涉阵列数字波束形成方法成为射电天文观测领域的技术难点。
本文首先介绍了SKA1-low的整体框架、射电望远镜具体参数及数据处理流程;然后,根据SKA1-low设计指标,提出两套数字波束形成方案,分别是基于多相滤波器组信道化数字相移波束形成(频域)和基于分数阶时延滤波器数字波束形成(时域);第3和4节分别详细介绍两套方案的原理和方法;最后,针对两套方案做了仿真实验分析,验证了两套方案的可行,并分析了不同阶数时延滤波器对波束的影响。
2 SKA1-low介绍
SKA1-low的射电望远镜由约131 072个对数周期双极化天线阵元的阵列组成,具体设计参数见表1。大多数阵元非常紧凑地排列在直径大约为1 km的区域,即核心阵。剩余的少数阵元则分布在大约几十米直径的台站内。这些台站将分布在半径超过40 km的Boolardy台站内,形成3个近似等距螺旋臂的构型,如图1所示。
表1SKA1-low对数周期偶极子天线
Tab.1 Log periodic dipole antenna of SKA1-low
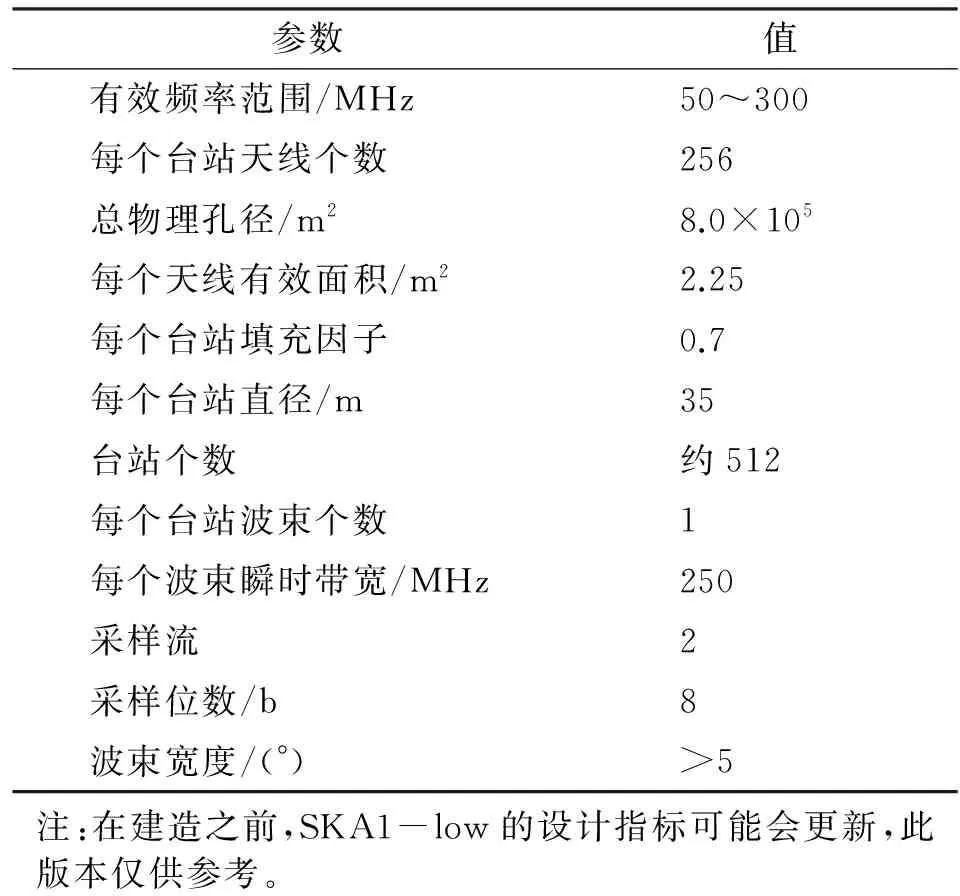
参数值有效频率范围/MHz50~300每个台站天线个数256总物理孔径/m28.0×105每个天线有效面积/m22.25每个台站填充因子0.7每个台站直径/m35台站个数约512每个台站波束个数1每个波束瞬时带宽/MHz250采样流2采样位数/b8波束宽度/(°)>5注:在建造之前,SKA1-low的设计指标可能会更新,此版本仅供参考。

图1SKA1-low天线分布图
Fig.1 SKA1-low antennas distribution
SKA1-low系统工作流程如图2所示。台站子系统完成波束形成,输出该台站波束信号。各个台站波束信号将传入到中央信号处理(CSP),进行信道化、校正,然后两两进行互相关运算,获得射电源的可见度数据。可见度数据进行射频干扰(Radio Frequency Interference,RFI)去除、初步校准和A项去除后,输出的信号将传入到科学数据处理中心(SDP)进行校准成像和图像分析,最终完成预期的科学目标。从图2可以看到,波束形成是整个SKA1-low处理流程的第一步,波束形成的结果将影响到后面的CSP和SDP流程,特别是对SDP中主波束校准的影响尤为重要。因此,对波束形成技术的研究可以为CSP和SDP部分关键技术提供理论指导。
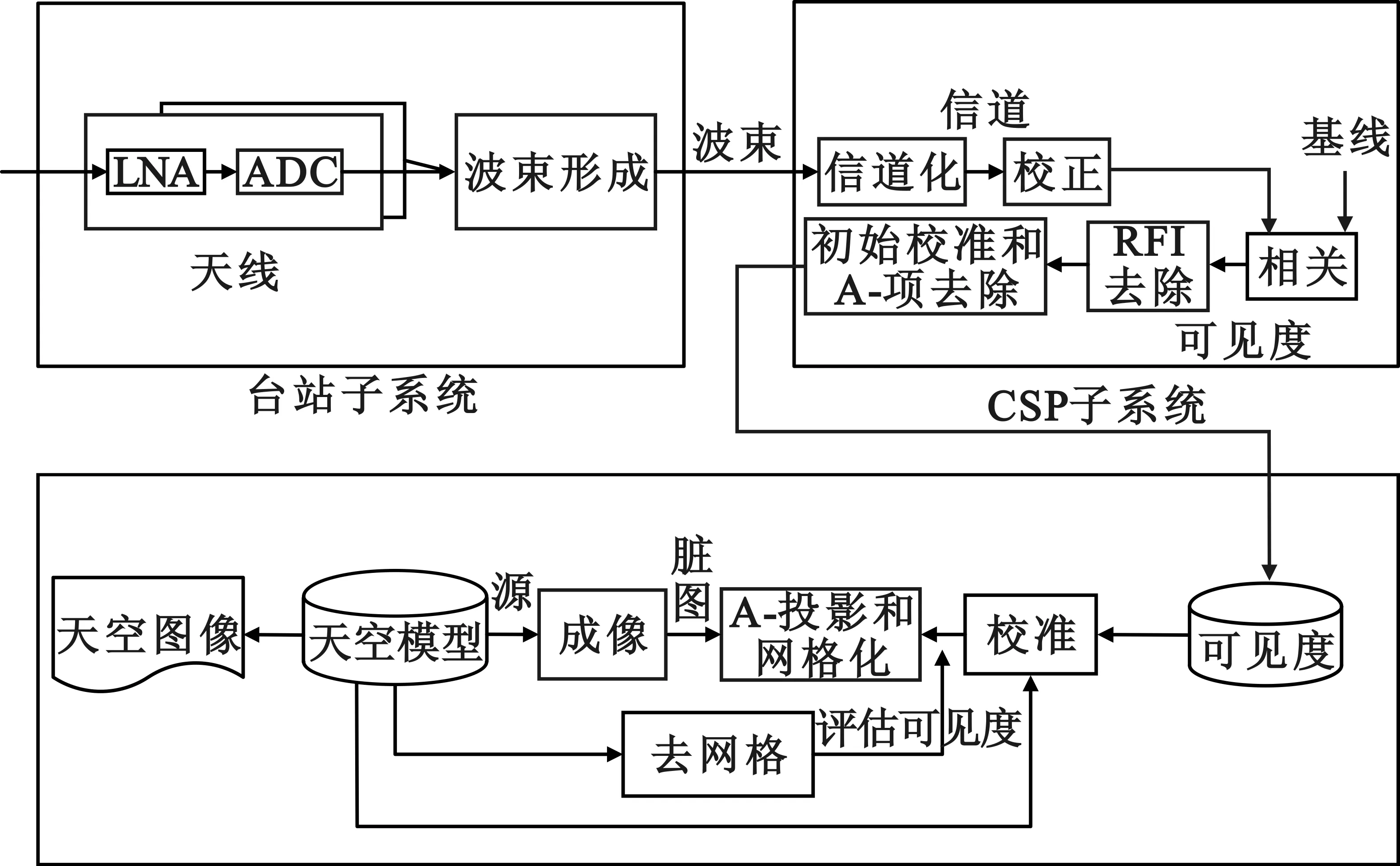
图2SKA1-low系统工作流程图
Fig.2 SKA1-low system workflow diagram
3 基于多相滤波器组信道化数字移相波束形成
波束形成又称为空域滤波器,其基本原理是通过将阵列各阵元输出进行延时加权求和(或同相叠加),在同一时间内将阵列波束导向一个方向上,对期望信号(或者感兴趣的方向信号)得到最大输出功率的导向位置。根据SKA1-low低频阵列的特点及设计指标,本文提出两种方法供相关科研人员参考,分别是频域和时域数字波束形成。根据各自的特点,我们把频域数字波束形成命名为基于多相滤波器组信道化数字相移波束形成,时域数字波束形成命名为基于分数阶时延滤波器数字波束形成。
SKA1-low接收的信号是带宽为300 MHz的宽带信号,此时需要对宽带信号进行信道化,把宽带信号化分为M个信道的窄带信号,这时再使用窄带信号数字波束形成理论[8]对每个信道的输出信号进行波束形成。因此,本文提出一种基于多相滤波器组信道化数字移相波束形成方案,基本原理如图3所示。图3中目标模拟信号经滤波、低噪放和A/D 采样后得到数字信号,数字信号进入FIR+FFT信道化,得到M个信道窄带信号,然后各阵元在相同信道下作天线校准和相位补偿,再进行求和,得到M个信道下的波束方向图。不同信道下各阵元的校准和相位补偿是不同的,会随着频率的变化而变化,所有信道下波束的集合将是时间和频率的一个函数。其中,M个信道的多相滤波器组信道化的数学模型如图4所示,详细的公式推导及原理分析见文献[9]。
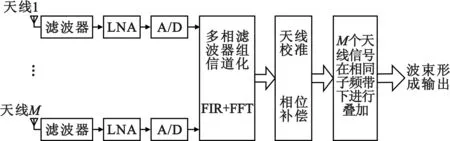
图3基于多相滤波器组信道化数字移相波束形成原理框图
Fig.3 Block diagram of digital polyphase filter bank channels based digital phase shift beamforming
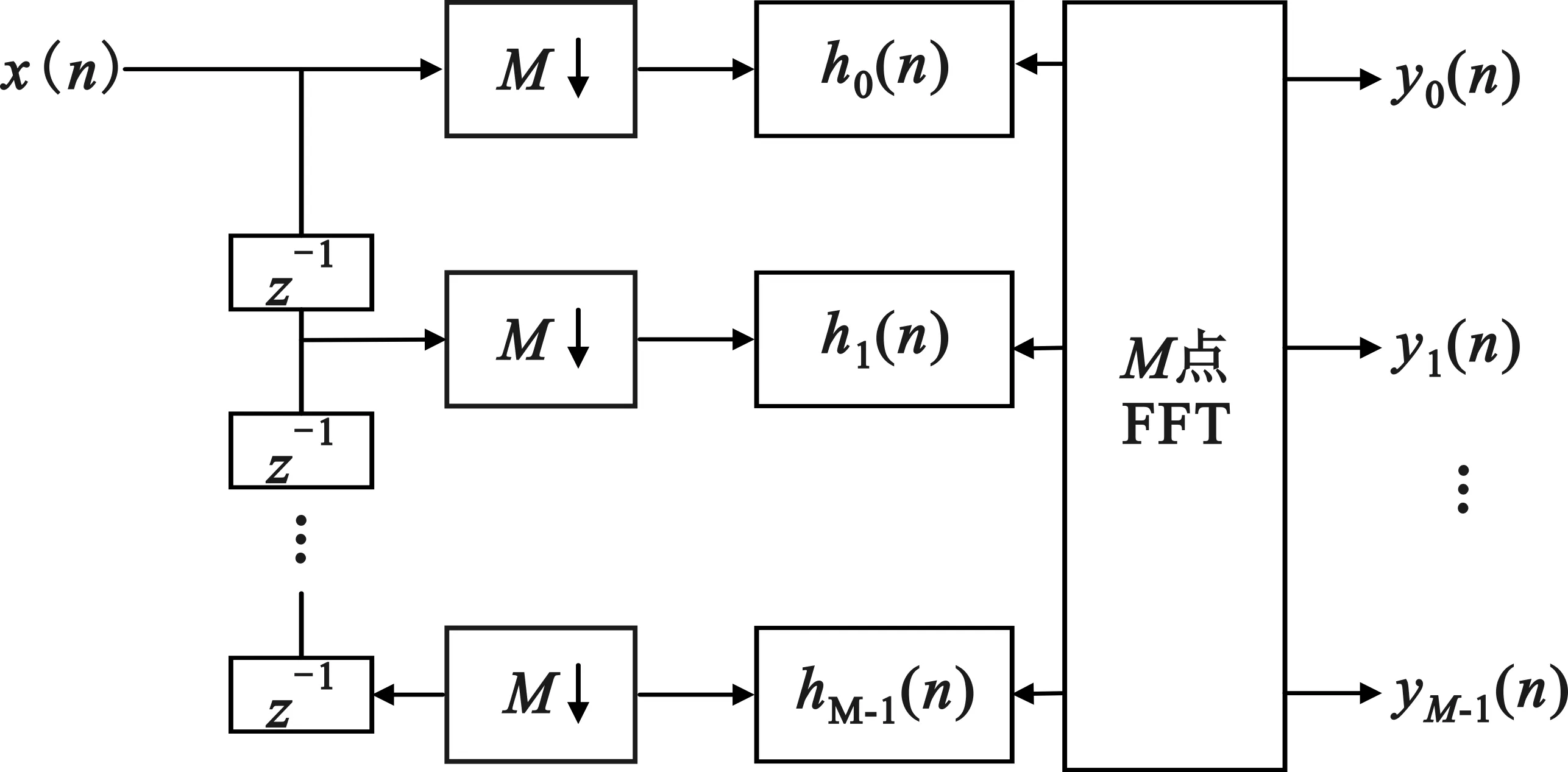
图4多相滤波器组信道化数学模型
Fig.4 The mathematical model ofpolyphase filter bank channels
根据图3的流程,接下来需要对信道化的结果进行阵列校准和相位补偿。本文使用的相位差求解方法是互相关法,这种方法的优势在于可以充分利用现有的SKA1-low系统CSP中的相关处理机部分来求解波束形成部分所需的相位差。
假设两个信号x1(t)和x2(t),分别对它们进行FFT之后得到X1(f)=Amejφ1和X2(f)=Bmejφ2,互相关表达式为
。
(1)
因此,互相关的相位即为两个信号的相位差。最后,把各个阵元相位补偿后的信号进行加权求和得到波束。此方案的主要优势:使用FIR+FFT信道化及数字相移,在计算速度方面存在明显优势,能够灵活控制波束指向,具备带通信号校准能力,适合用于大规模数字阵列。缺点是:各个信道的无缝连接要求高,此方案一般使用FPGA实现如天文信号处理与电子研究所(Collaboration for Astronomy Signal Processing and Electronics Research,CASPER)[10]制作的高速数据处理平台,成本较高。
4 基于分数阶时延滤波器数字波束形成
假设天线阵列由M个天线组成的面阵,第m个阵元在阵中的位置为(xm,ym,zm),如图5所示,选择坐标原点o作为相位参考点(z轴指向北天极方向)。其中R是阵列相位参考点到远区目标的距离,ΔRm是第m个天线单元到目标的距离与参考点到目标的差值,目标信号为s(t),波长为λ。

图5面阵模型
Fig.5 Planar array model
在图5所示的坐标中,假设第i个信号到达的方位角为φi,俯仰角为θi,目标方向为单位向量n=(sinθisinφi,sinθicosφi,cosθi),则第m个天线单元位置lm=(xm,ym,zm)到目标的距离与参考点到目标的差值ΔRm可表示为
ΔRm=xmsinθisinφi+ymsinθicosφi+zmcosθi=lm·n。
(2)
ΔRm对应的相位,即第m个单元相对参考点o的信号相位差Δφm为

(3)
ΔRm对应的延时,即第m个单元相对参考点o的信号时延Δtm为
Δtm=(lm·n)/c。
(4)
式中:c是光速。
在数字域中应用时,还要转换到数字域Δtm/ts,其中ts是采样时间。通过上式求得相对时延,最后求得M个天线的输出方向图为
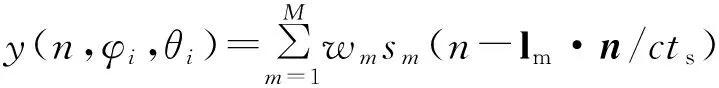
(5)
式中:wm是标量权重;sm(n)是由没有发生时延的入射信号s(t)进行采样得到的,即Sm(n)=s(t/ts)。从式(5)可以看出,该方法可以完成二维数字波束扫描。
从上面的分析知,要想求得波束方向图关键在于求解延时Δtm/ts,求解过程详见文献[11]。
本方案计算波束方向图的思路是: 对输入的信号进行分数阶延时补偿,然后进行加权求和。其主要优势:结构简单,易于实现,成本较低,比较适合于低频数字阵列验证性系统如21CMA,对于宽带信号此法非常有效。缺点:当需要对子采样同步时,会增加数字滤波器的设计复杂度;受采样速率限制,采样速率越高算法运行效率要求越高,否则容易丢失数据。
5 仿真结果与分析
5.1基于多相滤波器信道化数字移相波束形成仿真
设计均匀阵列的输入信号为
S=cos2nπf1+(2+cos2nπf2)cos2nπ·50+
sin2nπf3cos2nπ·100+cos2nπf5cos2nπ·200。
式中:f1=3 MHz,f2=5 MHz,f3=10 MHz,f5=15 MHz;采样频率fs=500 MHz;天线个数为19个。低通滤波器原型利用MATLAB中的remezord函数和remez函数确定。阵列的输入信号及其频谱如图6所示,谱线分别位于3 MHz、55 MHz、110 MHz和215 MHz。经多相滤波器信道化后数字基带信号输出如图7所示。由于实信号输入,根据对称性,只需要10个信道中的5个信道就包含了全部信息。

图6输入信号及其频谱
Fig.6 Time-domain and frequency-domain response of input signal
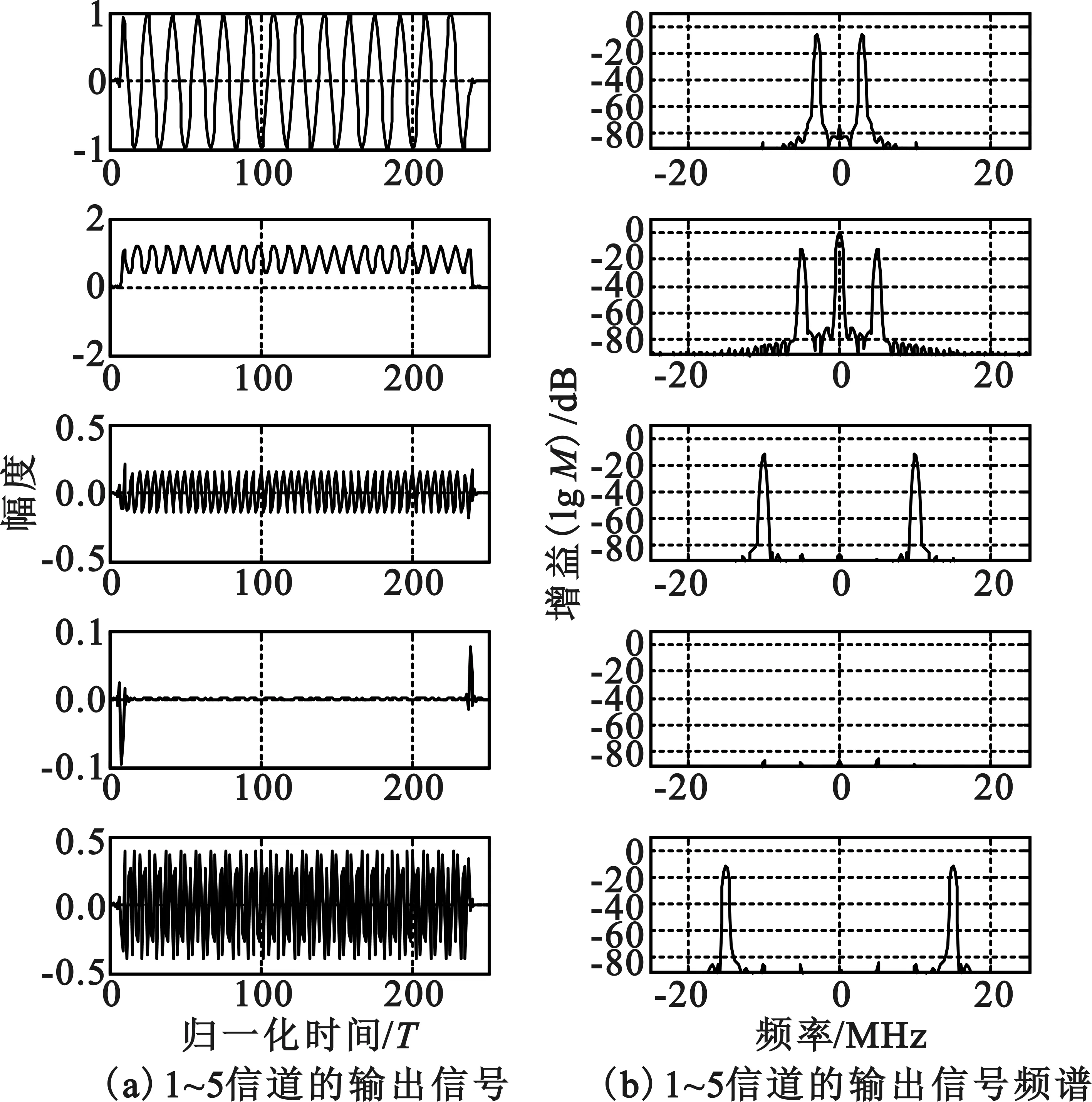
图7多相滤波器信道化输出结果
Fig.7 Channelization output results
由图7的仿真结果可见:每个信道带宽50 MHz,第一个信道的中心频率是0,处于该信道的基带信号频率f1=3 MHz;第二个信道的中心频率是50 MHz,处于该信道的除了基带信号频率f2=5 MHz,还有一直流信号;第三个信道的中心频率是100 MHz,处于该信道的基带信号频率是f3=10 MHz;第四个信道的中心频率是150 MH,这一信道无基带信号;第五个信道的中心频率是200 MHz,处于该信道的基带信号频率是f5=15 MHz。各信道输出信号与输入信号一致。
此实验期望信号指向为21°。选取第三个信道下各个阵元的输出信号,以第一个阵元输出信号作为参考信号,依次与其余信号进行互相关运算计算出其余阵元与参考阵元的相位差Δφ,其余阵元输出信号在频域上乘以对应ejΔφ进行相位补偿(这里幅度不变,幅度权重为1),然后进行叠加,最后计算出时域方向图如图8蓝色线所示,使用传统的数字移相波束形成算法得到的波束方向图如图8红色线所示。经计算,本文算法得到的波束指向为20.9°,-3 dB主波束宽度约为4.9°,旁瓣强度约为-13.18 dB;传统算法得到的波束指向为20.7°,-3 dB波束宽度为4.8°,旁瓣强度约为-12.3 dB。仿真结果表明本文算法比传统算法得到的波束指向更精确,性能更好,同时验证了本文算法的正确性。

图8波束方向图
Fig.8 Beam pattern
5.2分数阶时延数字波束形成仿真
5.2.1算法验证
设计一个边长为2.8 m的正六边形阵列,中心在原点,天线总数为19,位于xoy平面(z=0),最终天线布局如图9所示。阵列的入射信号为单色平面波,频率为150 MHz,期望指向为(30°,30°)。采样频率为400 MHz,分数阶时延滤波器的阶数为50。
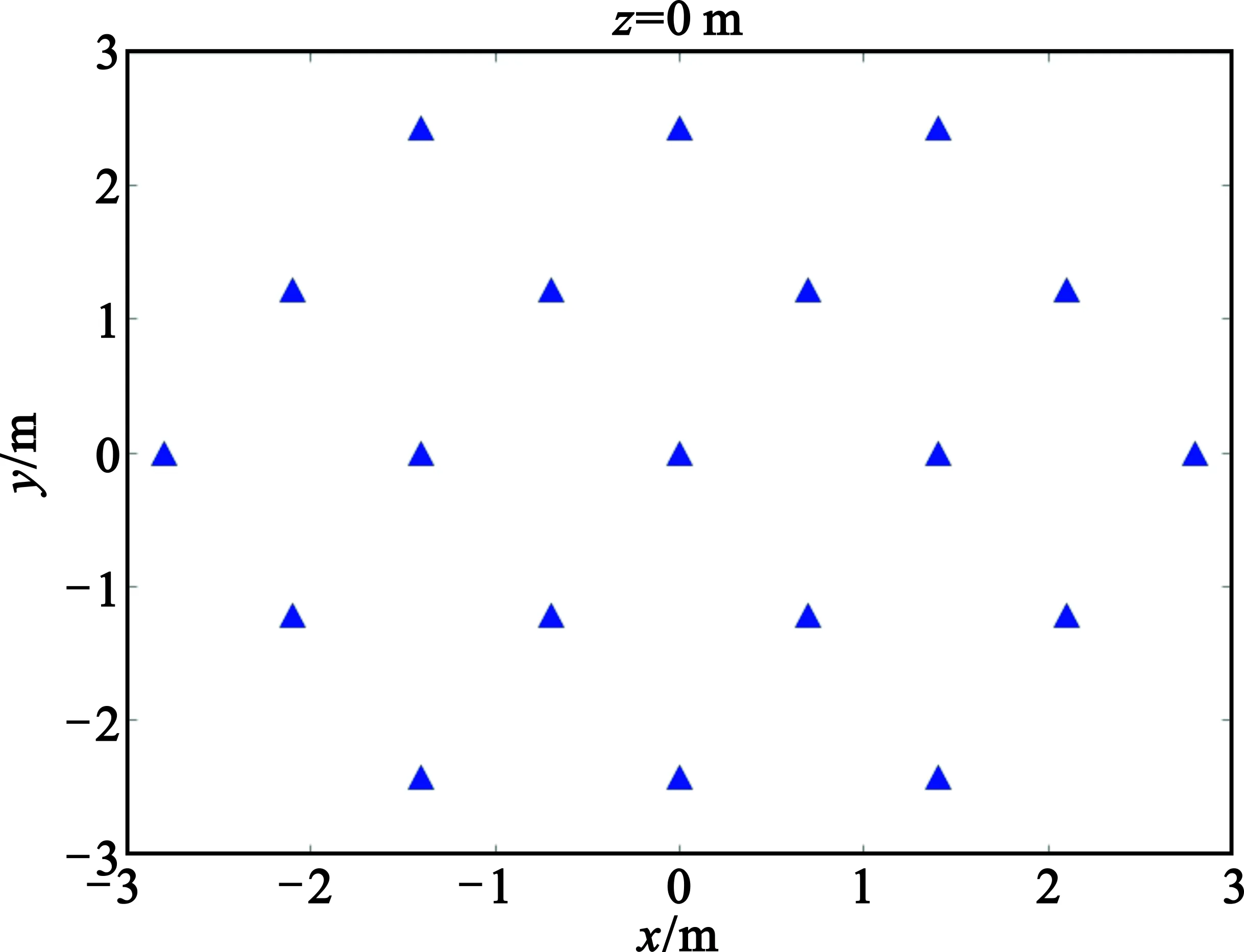
图9正六边形阵列布局图
Fig.9 Layout diagram of regular hexagonal array
最终得到的波束方向图如图10和图11所示,分别是三维形式和灰度形式。波束指向:俯仰和方位角分别为29.9°和29.8°,指向与期望信号方向一致,表明基于分数阶时延滤波器数字波束形成是正确的。但该方案耗时过长,在实际系统中,如果每个采样数据进行波束形成所消耗时间大于采样周期时,将会丢失部分采样数据,这有可能导致后续的数据处理过程产生误差。对于小型阵列我们可以通过优化软件编程算法提高其运行速率,从而缩短算法运行时间;对于大规模阵列如SKA,在优化算法本身的同时还需要将算法改进为基于消息传递接口(Message Passing Interface,MPI)、图形处理器(Graphic Processing Unit,GPU)和众核技术(Many Integerated Core,MIC)等并行计算的波束形成算法,才能有效提升算法运行速率。基于MPI的改进算法的主要思路是将每个天线的数据处理过程(时延补偿等)分别放在不同的进程下进行,然后将不同进程的处理结果广播到主进程进行叠加并输出波束结果。基于MIC的改进算法,只需要将波束形成算法使用MIC编程重新编写,可以由实际情况考虑使用不同的MIC应用模式(原生、对等、offload等模式)。基于GPU的改进算法,主要是使用统一计算机设备架构(Compute Unified Device Architecture,CUDA)和开放计算语言(Open Computing Language,OpenCL)编程技术将原始算法重新改写为并行运行的算法。

图10三维形式波束图
Fig.10 Three-dimensional form beam pattern

图11灰度形式波束图
Fig.11 Grayscale form beam pattern
5.2.2分析不同阶数时延滤波器的影响
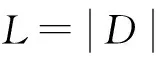

图12不同阶数时延滤波器下波束宽度和第一旁瓣衰减变化曲线
Fig.12 A variation curve beam width and the first side lobe attenuation under different order filter
6 结束语
本文针对SKA1-low的设计指标提出了两套数字波束形成方案,以期为我国相关科研人员提供技术参考。在明确了SKA1-low设计指标后,详细介绍了两套方案的原理及其优缺点。设计了不同天线阵及入射信号进行仿真实验,结果充分证明了两套方案能够准确地完成数字波束形成,得到的波束图指向符合预期。在分析不同阶数时延滤波器对波束影响时,得出了分数阶时延滤波器的最佳阶数N应满足N=2|D|max,其中D为数字时延量。基于多相滤波器组数字移相波束形成方法实际应用中一般采用射电天文高速数据采集与处理平台如CASPER来实现,能够快速精确完成各模块信号处理,灵活产生多波束,波束精度较高,比较适用于大规模数字阵列如SKA;基于分数阶时延滤波器数字波束形成方法受采样速率限制,天线数目越多对算法运行效率要求越高,适用于个数比较少的验证天线系统,比如21CMA,但需要解决计算数据丢失等问题。在后续的仿真工作中,将扩大阵列天线个数,在计算量增加的情况下将会考虑使用并行化计算方法提高算法运行效率。
[1]彭勃,金乘进,杜彪,等.持续参与世界最大综合孔径望远镜 SKA 国际合作[J].中国科学: 物理学 力学 天文学,2012,42(12): 1292-1307.
PENG Bo,JIN Chengjin,DU Biao,et al.China's participation in the SKA the world's largest synthesis radio telescope[J].Scientia Sinica:Pysica,Mechanica & Astronomica,2012,42(12):1292-1307.(in Chinese)
[2]TASSE C,DIEPEN G V,TOL S V D,et al.LOFAR calibration and wide-field imaging[J].Comptes Rendus Physique,2012,13(1): 28-32.
[3]HAARLEM M P V,WISE M W,GUNST A W,et al.LOFAR: the low-frequency array[J].Physics,2013,556(7):629-635.
[4]KAPLAN D L,TINGAY S J,MANOHARAN P K,et al.Murchison widefield array observations of anomalous variability: a serendipitous night-time detection of interplanetary scintillation[J].The Astrophysical Journal Letters,2015,809(1):1-7.
[5]ZARB-ADAMI K,FAULKNER A,KANT G W,et al.Beamforming techniques for large-N aperture arrays[C]//Proceedings of 2010 IEEE International Symposium on Phased Array Systems and Technology(ARRAY).Walcham,MA:IEEE,2010: 883-890.
[6]MOL J D,ROMEIN J W.The LOFAR beam former: implementation and performance analysis[J].Lecture Notes in Computer Science,2011,6853(2): 328-339.
[7]TINGAY S J,GOEKE R,BOWMAN J D,et al.The murchison widefield array: the square kilometre array precursor at low radio frequencies[J].Publications of the Astronomical Society of Australia,2013,30(30):109-121.
[8]SHAKIR M Z,DURRANI T S.Narrowband beamforming algorithm for smart antennas[C]//Proceedings of 2007 International Bhurban Conference on Applied Sciences & Technology.Islamabad:IEEE,2007: 49-54.
[9]陈岚,张秀忠.用于VLBI数字基带转换的多相滤波器技术研究[J].天文学进展,2008,26(1): 87-94.CHEN Lan,ZHANG Xiuzhong.The study of DBBC based on poly-phase filter banks and FFT in VLBI[J].Progress in Astronomy,2008,26(1): 87-94.(in Chinese)
[10]ARMSTRONG R,HICKISH J,ZARB ADAMI K,et al.A digital broadband beamforming architecture for 2-PAD[J].Physics,2010,13(3):185-189.
[11]VALIMAKI V,LAAKSO T.Fractional delay digital filters[C]//Proceedings of 1993 IEEE International Symposium on Circuits and Systems.Chicago,IL:IEEE,1993: 355-359.

劳保强(1989—),男,广西北海人,2015年于桂林电子科技大学获工学硕士学位,现为工程师,主要研究方向为SKA1-low数字波束形成技术和存储底层IO并行技术;
LAO Baoqiang was born in Beihai,Guangxi Zhuangzu Autonomous Region,in 1989.He received the M.S.degree from Guilin University of Electronic Technology in 2015.He is now an engineer.His research concerns SKA1-low digital beamforming techniques and underlying storage IO parallelism.
Email: lbq@shao.ac.cn
安涛(1979—),男,河北任县人,2004年于中国科学院上海天文台获理学博士学位,现为研究员,主要研究方向为射电天文技术;
AN Tao was born in Renxian,Hebei Province,in 1979.He received the Ph.D. degree from Shanghai Astronomical Observatory,Chinese Academy of Sciences in 2015.He is now a senior engineer of professor.His research concerns radio astronomy technology.
Email: antao@shao.ac.cn
郭绍光(1985—),男,山东聊城人,2011年于中国科学院新疆天文台获理学硕士学位,现为工程师,主要研究方向为硬件相关处理机技术;
GUO Shaoguang was born in Liaocheng,Shandong Province,in 1985.He received the M.S. degree from Xinjiang Astronomical Observatory,Chinese Academy of Sciences in 2011.He is now an engineer.His research concerns hardware correlator technology.
Email: sgguo@shao.ac.cn
魏延恒(1990—),男,山东德州人,2015年于桂林电子科技大学获工学硕士学位,现为工程师,主要研究方向为大视场成像技术;
WEI Yanheng was born in Dezhou,Shandong Province,in 1990.He received the M.S. degree from Guilin University of Electronic Technology in 2015.He is now an engineer.His research concerns wide-field imaging technology.
Email: wyh@shao.ac.cn
陆扬(1985—),男,上海人,2014年于加拿大多伦多大学获经济学硕士学位,现为中国科学院上海天文台工程师,主要研究方向为射电天文技术;
LU Yang was born in Shanghai,in 1985.He received the M.S. degree from University of Toronto,Canada,in 2014.He is now an engineer.His research concerns radio astronomy technology.
Email: ylu@shao.ac.cn
伍筱聪(1989—),男,浙江金华人,2011年于浙江工业大学获工学硕士学位,现为中国科学院上海天文台工程师,主要研究方向为射电天文技术。
WU Xiaocong was born in Jinhua,Zhejiang Province,in 1989.He received the B.S. degree from Zhejiang University of Technology in 2011.He is now an engineer.His research concerns radio astronomy technology.
The National Key Basic Research Program of China(973 Program)(2013CB87900);The National Natural Science Foundation of China(No.11403081);The Observatory Station Equipment Update and Major Equipment Operation Program of Chinese Academy of Sciences(No.587121002)
Digital Beamforming Techniques Based on SKA1-low
LAO Baoqiang,AN Tao,GUO Shaoguang,WEI Yanheng,LU Yang,WU Xiaocong
(Shanghai Astronomical Observatory,Chinese Academy of Sciences,Shanghai 200030,China)
In order to coordinate China’s participation in Square Kilometre Array(SKA) and gain depth understanding of radio interferometry and data processing algorithm based on digital beamforming,the polyphase filter bank channels based digital phase shift and the fractional delay filter based digital beamforming algorithms are proposed in this paper.The former algorithm solves the phase shift amount by using a cross-correlation method to improve the beam pointing accuracy.The latter algorithm is an effective combination of traditional algorithm and radio observations theory.Firstly,the principles of the proposed algorithms are derived and the advantages and drawbacks of the two algorithms are analyzed.Secondly,the simulation results are shown to verify the correctness of the proposed algorithms.Simulation results indicate that the proposed polyphase filter bank channels based digital phase shift beamforming has certain advantages in comparison with traditional algorithm.Finally,the effect of delay filter of different orders on beamforming is also analyzed.These simulation results and conclusions will provide reference for the researchers of SKA project.Key words:square kilometre array project;low-frequency array;digital beamforming;polyphase filter;fraction delay
10.3969/j.issn.1001-893x.2016.09.002
2016-02-26;
2016-05-04Received date:2016-02-26;Revised date:2016-05-04
国家重点基础研究发展计划(973计划)项目(2013CB87900);国家自然科学基金资助项目(11403081);天文台站设备更新及重大仪器设备运行专项经费资助项目(587121002)
TN820
A
1001-893X(2016)09-0956-07
Email:xbtan@ustc.edu.cn
引用格式:劳保强,安涛,郭绍光,等.基于SKA1-low的数字波束形成技术[J].电讯技术,2016,56(9):956-962.[LAO Baoqiang,AN Tao,GUO Shaoguang,et al.Digital beamforming techniques based on SKA1-low[J].Telecommunication Engineering,2016,56(9):956-962.]
**通信作者:lbq@shao.ac.cnCorresponding author:lbq@shao.ac.cn
