别让数学实验“形同虚设”——以分组合作方式，用数学建模思想探究二次函数实验

□海南省万宁市民族中学陈辉亮

别让数学实验“形同虚设”
——以分组合作方式，用数学建模思想探究二次函数实验

□海南省万宁市民族中学陈辉亮

一、提出课题

现在许多家庭都是以煤气为燃料，日常生活烧水、做菜、做饭，都少不了煤气，如何才能使得用气最少？以下就以烧一壶水为例，分组合作探究这个问题。

二、学生探究

各小组讨论并发表意见：烧水过程煤气的用量与什么因素有关？

组1：煤气燃烧时与热效率有关，热效率是指它对水直接加热的能量与在空气中消耗的总能量的比值，比值越大说明热效率就越高，还可以说和燃烧时间长短有关，时间越长热效率越低，时间越短热效率越高。

组2：是否是完全燃烧，与水的初始温度有关；还和水的多少有关。

组3：与水壶的效率有关，水壶的保温效果好，那么散热少，水烧开就快，煤气用量相对来说就少。

组4：和当时的大气压强有关，还和煤气的质量有关，质量好的煤气当然用量就会少。

教师分析：假定在一个理想的条件下，相同的一壶水，相同的煤气质量，而且保证水的初始温度一样，相同的一个外部环境，排除上面这些因素的干扰，那么这时候问题就转化成煤气灶的旋钮要转到什么位置时烧开这样的一壶水煤气的用量最少？会是火很大还是火很小呢？

三、确定实验方案

各组分别设计实验方案，讨论选择最合理方案进行实验。

组1：取两个水壶一样，控制水的质量、初温一样，分别放在两个燃气灶上加热，旋钮旋转不同的角度观察哪边先烧开。

组2：取一个水壶，放上一定质量的水，使水的初温一定，加热至烧开，测量水烧开的时间是多少，接着把水壶水倒掉，让水壶冷却到原来的温度，再加入相同质量、温度的水，这时将旋钮转到不同位置，记录水烧开所需要的时间。

组3：设计方案分三次来进行，假设每次所用的煤气是一样的，然后分别将旋钮转到大火、中火、小火的位置；待到预先设置的煤气用完，分别测量水温升高了多少，进行比较，得出效率，就可以判断出来什么火时是最节省煤气的。

组4：方案是在组3的基础上进行了改良设计，用到了煤气表的读数，我们分别取五个不同位置的角度180、360、540、720、900进行实验，控制相同的条件下使水烧开，分别记录燃气表开始时和水开时的读数，通过对比，就可以判断出来旋钮旋转到什么位置时是最节省煤气的。

四、实验

根据小组讨论确定的实验方案，选取五个不同角度18°、36°、54°、72°、90°进行实验。实验数据记录如下：

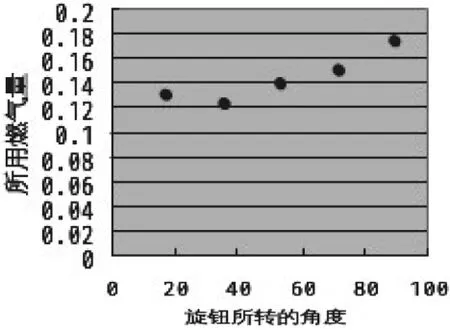
为了更形象地反映数据特征，我们以旋转角度为横坐标，所用燃气为纵坐标作散点图如下图。

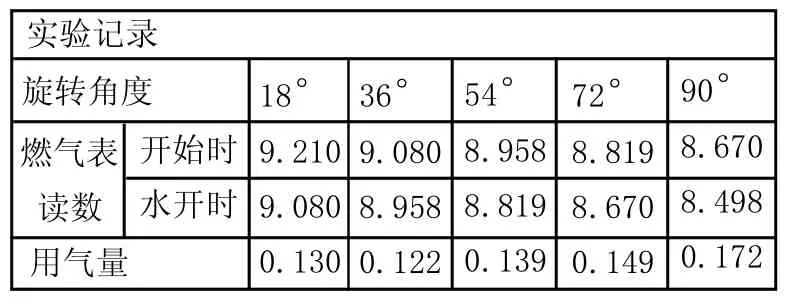
实验记录旋转角度燃气表读数开始时水开时用气量1 8 ° 9 . 2 1 0 9 . 0 8 0 0 . 1 3 0 3 6 ° 9 . 0 8 0 8 . 9 5 8 0 . 1 2 2 5 4 ° 8 . 9 5 8 8 . 8 1 9 0 . 1 3 9 7 2 ° 8 . 8 1 9 8 . 6 7 0 0 . 1 4 9 9 0 ° 8 . 6 7 0 8 . 4 9 8 0 . 1 7 2

五、实验结果检验

从散点图的趋势来看，各小组学生经过思考、分析、归纳、对比学过的函数图像中，一元二次函数图像与之最相似，故学生认为可以用一元二次函数近似地表示这种变化，于是问题就转化成研究二次函数；我们先假设二次函数的解析式为y=ax2+bx+c，根据函数解析式我们可以算出当旋钮旋转到什么位置时，煤气的用量最少，最少是多少的问题。

为了确定a，b，c三个常数的值，在选取点方面学生展开了激烈的讨论。

组2：取最低点和最高点，还有中间一点，也就是第二、三、五个点。

组3：我们组讨论认为第三个点在函数图像中应该算是误差点，如果是画图像的话，第三个点可能不在图像上，所以排除第三个点，选取第一、二、五个点。

1.拟合函数。设函数y=ax2+bx+c，取（18，0.130），（36，0.122），（90，0.172）代入函数得方程组

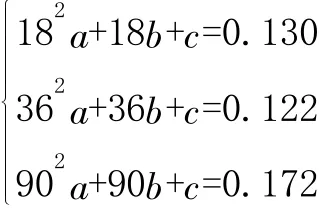
解得：a=1.9033×10-5；b=-1.4722×10-3；c=0.15033

则函数式为：y=1.9033×10-5x2-1.4722×10-3x+0.15033

2.求最少用气量。求解得燃气用量最少时旋钮的实际位置是：

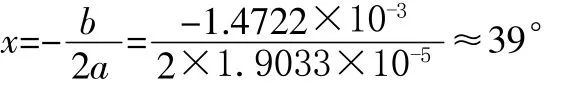
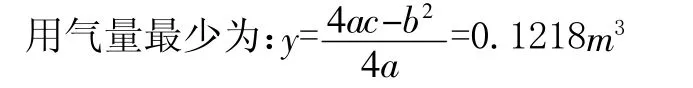
3.检验分析。学生们展开了新一轮的讨论。

组1认为：分别在39°和另外取一角度80°烧同一壶水，再记录煤气表的用量。

组4认为：代个数字进去，代刚才五个量里的一个，除了误差点那个，即第四个点。

学生总结：组1的检验方法是错误的，因为比较时不能就取两个值，关键是这个不能比较，就是不一定能试到最小的，这样比较的没有代表性；而组4的检验方法比较合理，它直接刻画这个数学模型是否符合实际问题。

六、实验反思

此次数学实验让学生体会到如何由实际的问题抽象出数学问题，以小组合作方式进行探究、实验、归纳、建立数学模型、解决问题。培养学生对“形”的把握能力，通过“形”来处理数据，培养学生动手实验能力，利用多媒体软件技术拟合函数等综合能力。渗透数形结合的思想方法，发展了学生“想用、能用、会用”的数学知识意识，培养了学生求真、求实、创新、严谨的科学精神，但本实验也存在不足之处，实验耗时比较长，可以分两个阶段进行，对实验操作要求比较高，数据要合理规范和学生要有较高的个人综合处理能力。