基于最优分配策略的弹道导弹目标关联算法

马　敏，靳俊峰

(1.中国电子科技集团公司第三十八研究所，合肥 230088；2.孔径阵列与空间探测安徽省重点实验室，合肥 230088)



基于最优分配策略的弹道导弹目标关联算法

马敏1,2，靳俊峰1,2

(1.中国电子科技集团公司第三十八研究所，合肥 230088；2.孔径阵列与空间探测安徽省重点实验室，合肥 230088)

为突防需要，弹道导弹目标在飞行过程中会释放多批诱饵、假弹头等形成群目标进行伴飞。由于群内目标之间相互靠近且运动特性相似，跟踪过程中极易发生混批、错批等问题，导致无法尽早进行轨道推算、目标识别等，缩短了导弹拦截时间。本文提出了基于最优分配策略的目标关联算法。首先将目标关联问题归纳为最优分配的一种特例，然后根据目标归一化残差、速度、航向、AD值等信息综合计算关联概率并构建关联代价矩阵，最后对关联代价矩阵进行最小化求解，计算最优的量测和航迹配对。仿真分析结果表明该算法能够大幅度提高群内目标关联准确性。

最优分配；弹道导弹目标跟踪；数据关联；综合隶属度

0　引　言

自二战末期弹道导弹问世以来，世界各国便竞相研制各种进攻性导弹。高密度、高强度的导弹战将成为战争初期或关键时刻的主要方式。同时,为了增强导弹的突防能力，各种隐身技术、电磁干扰技术、诱饵、弹头机动变轨技术等突防措施也纷纷被采用。由于弹头目标周围经常有诱饵、假目标等伴飞，在空间形成相互靠近的群目标，导致在目标跟踪过程中经常出现混批、错批，给后续的目标识别、轨道外推等带来很大难度。如何解决群内目标正确关联是弹道导弹防御中的核心问题。

迄今为止，已经有很多有效的数据关联算法，包括Singer在70年代初期提出的最近邻域法(NN)[1]。它是一种最简单数据关联算法，也是在稀疏杂波环境下最有效的关联算法之一，但该算法在杂波较大时关联正确率较低。虽然Singer又在最近邻算法的基础上增加了虚警率、跟踪门等约束条件，但仍没有解决离预测位置最近的量测不一定是正确量测这个根本问题。Bar-Shalom等认为不能直接地将离预测位置最近的量测作为正确量测来更新目标状态，而是应该考虑关联门内所有的量测加权，提出了适用于杂波环境中对目标进行跟踪滤波的概率数据关联算法(PDA)。相比NN算法，PDA算法由于考虑了所有有效回波，关联准确性较高。但是，在密集目标环境下，PDA算法不考虑相交波门内的公共量测，容易产生对目标的误跟或失跟。所以，这种关联算法仅适用于对单目标的跟踪。后续Bar-Shalom又提出了联合概率数据关联(JPDA)[2]。该方法是在杂波环境下同时对多个目标进行数据关联跟踪处理的一种良好算法，但也存在着计算量大、实时性差以及近距离运动目标航迹合并等局限性。

此外，基于似然函数的数据关联算法主要包括的最大似然数据关联算法、0-1整形规划法、航迹分裂法等也得到了很大发展[3-6]。最大似然数据关联算法是针对不同目标的量测服从某种特定的概率分布但是未知参数不同的情况，通过最大似然原理利用最大似然估计法得出相应的未知参数，然后将量测和目标关联。

本文提出的算法正是结合最近邻思想和极大似然函数算法，将弹道导弹目标关联问题归纳为一种最优化问题，并采用最优分配算法进行点航迹配对，大幅度提高了群内目标的关联正确率。

1　关联矩阵

1.1隶属度函数

若对论域U中的任一元素x都有一个数A(x)∈(0,1]与之对应，则称A为U上的模糊集，A(x)称为x对A的隶属度。隶属度A(x)越接近于1，表示x属于A的程度越高，越接近于0表示x属于A的程度越低。对弹道导弹目标来讲，其特征参数包括归一化距离、速度、航向、AD值等，且都是连续型的因素变量。目标关联的本质是找到正确的隶属度函数。量测属于航迹时特征参数的隶属度接近于1，否则特征参数的隶属度应接近于0。由于弹道导弹特征变量可以认为是正态分布模糊集，航迹i与量测j的第l个特征参数xl关联的隶属度函数可以选择用柯西型分布函数[7]：

(1)

1.2决策向量

根据公式(1)的隶属度可以构造决策向量:

(2)

(1)ul∈[0,1],表示k时刻量测j的第l个特征参数xl与航迹i关联的概率，已经进行了归一化；

(2)uq和up互不关联(q≠p),表示任一隶属度的改变，不影响另一隶属度；

(3) 当增加一个新的可用来衡量目标的特征参数时，可以只根据新目标的特性和相应的特征参数建立相应的评判函数。

(3)

1.3关联矩阵

(4)

关联概率dij若小于阈值Pth，则认为航迹i与量测j无法关联，在关联矩阵中取值为0；若大于Pth，则可用于构建基于综合隶属度函数的关联矩阵IM：

(5)

其中，n表示航迹数，m表示量测数。本节中的综合隶属度函数是传统预测波门的一种抽象表示，既可以表示航迹的预测位置，也可以表示预测速度、航向、AD值等更多的意义。在未来相控阵雷达功能越来越多、能力越来越强的发展趋势下，量测的信息会比以往更丰富，因此本文的算法具有良好的扩展性。

2　基于综合多因子关联矩阵的最优分配算法

2.1问题描述

弹道目标关联问题采用第一节中的综合隶属度函数表示为关联矩阵后，对时刻k所有的量测与航迹关联的核心就是如何对关联矩阵进行分配。该分配问题可描述如下：

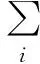
在分配算法中，允许xij为0或者1。如果量测数少于航迹数，则会出现有些航迹无法分配到量测，否则会出现量测无法关联到航迹。

对代价最小分配问题采用一种最优分配算法解决，步骤如下：

(1) 首先对关联矩阵CM采用聚类算法进行分簇，满足簇内的量测与航迹代价小于最大值，而簇间的量测与航迹代价大于最大值。通过分簇可将规模较大的分配问题转换为规模较小的分配问题，减少计算量；

(2) 对关联代价矩阵CM每一行，找出代价最小的元素rowmin，并将该行中的所有元素减去该值；

(3) 对关联代价矩阵CM每一列，找出代价最小的元素colmin，并将该列中的所有元素减去该值；

(4) 比较矩阵行数n和列数m，不妨假设行数n小于列数m，统计最少需要多少直线来覆盖结果矩阵中出现的所有零值。如果此时的零值个数与n相同，找到最优分配，矩阵计算结束，否则转第5步；

(5) 找出第4步中未被直线覆盖的最小非零值a，所有未被覆盖的元素减去a，对于被两条直线交叉覆盖的非零元素加a，重复第4步。

2.2求解示例

假设k时刻4个量测和4个航迹构建的代价矩阵如表1所示。

表1　关联代价矩阵

解决步骤如下：(1) 进行分簇处理，本示例中量测与航迹代价均小于最大值，分簇结果与表1相同。(2) 找出每一行中的最小值，并且该行中的所有元素均减去该值，例如第一行最小值为0.69。经过第2步计算结果如表2所示。

表2　算法第2步结果

(3) 每一列中减去该列的最小值，结果矩阵如表3所示。

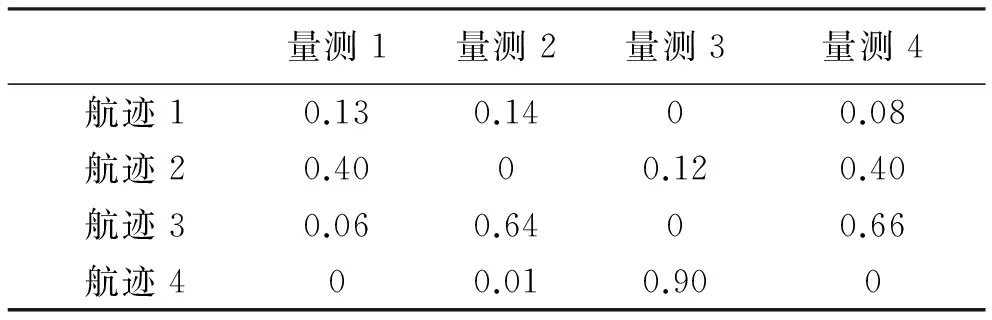
表3　算法第3步结果

(4) 统计覆盖所有零值需要的最少直线数，阴影表示直线，如表4所示。

表4　算法第4步结果

由于最少需要3条直线，小于矩阵的最小值4，因此需要进行第5步；

(5) 未被直线覆盖的元素中最小值为0.06，因此所有未被覆盖的元素均减0.06，被两条直线交叉覆盖两次的非零元素加0.06，结果如表5所示。

表5　算法第5步结果

(6) 转到第4步，再次统计覆盖零值的最少直线数，此次最少需要4条直线(阴影部分)，与矩阵的最小行或列数相同，找到了最优的分配，算法停止，最优分配结果如表6所示。

表6　算法第6步结果

本示例中的量测与航迹的配对结果如下：

航迹1，量测3；航迹2，量测2；航迹3，量测1；航迹4，量测4。

3　性能评估

由于弹道导弹测量数据密级较高，数据获取比较困难，采用仿真数据对基于综合隶属度的最优分配算法的性能进行验证。假设雷达的距离测量精度σr=30 m，方位测量精度σa=0.2°，仰角测量精度σe=0.15°，发现概率Pd=0.9，虚警概率Pf=1e-6，杂波分布服从泊松分布，滤波器采用基于弹道导弹动力学的UKF滤波方法[8-12]。弹道导弹在飞行过程中有两批假目标伴飞，3个目标距离间隔在500～1500 m之间，方位和仰角接近，且经常交叉，空间上形成了导弹群目标，导弹飞行时长80 s。

经过对仿真数据分析，群内的3个目标在距离上相对位置比较稳定，航向、速度、AD值等特征参数比较接近，因此在权向量选择上归一化距离特征具有最大的权重，达到了0.7，而其他特征由于无法明显区分目标，仅占比0.3。如果权向量选取不当，如归一化距离权值很小，而航向、速度、AD等权值很大，就会导致跟踪过程中出现错误关联。权向量的参数选择需要结合雷达体制、目标类型、飞行阶段等信息。在本次仿真中未考虑雷达测速。如果能够准确测量目标多普勒信息，则该信息也能够明显区分目标。

图1为采用最优分配算法的弹道导弹群目标关联结果。在目标观测初始阶段，3批目标会关联少数杂波。这是由于此时滤波器还未收敛，预测波门不准确导致归一化距离发生跳动。但是，一旦滤波器收敛后，综合隶属度函数解算的关联概率趋于稳定，此时采用最优分配算法分配后可发现3批目标平行飞行，不会发生关联杂波情况。

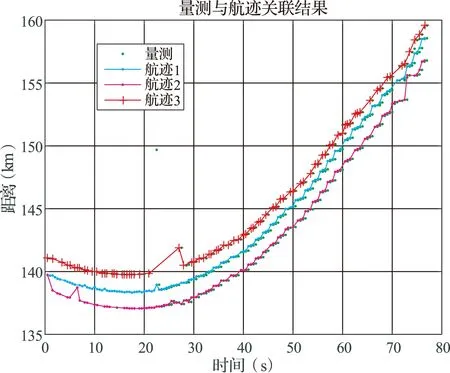
图1　3批目标关联分配结果

图2为采用基于弹道导弹动力学的UKF滤波方法对3批目标进行滤波结果。可以看出，在错误关联到杂波时，滤波器输出的距离并没有发生剧烈跳动。这是由于UKF滤波器采用了弹道动力学模型进行预测，不会因为少数奇异值导致滤波器波动，距离经滤波后明显比观测值平滑。

图2　3批目标跟踪滤波结果

4　结束语

弹道导弹目标在飞行过程中会释放多批诱饵、假弹头等形成群目标进行伴飞。由于群内目标之间相互靠近、运动特性相似和互相遮挡等原因，跟踪过程中极易发生混批问题。这也是目前弹道导弹防御系统面临的最大难题，即多目标饱和攻击。如果在跟踪过程中无法对群内目标进行正确相关，将无法进行后续的轨道推算、目标识别等进一步处理。错误的相关会导致无法正确识别弹头目标，雷达的资源会分散在多个假目标上，最终弹道导弹防御系统面临能量枯竭，错失了拦截导弹的最优时间。本文提出了基于最优分配策略的目标关联算法。首先对数据关联问题进行数学分析，将传统的量测-航迹配对问题归纳为采用综合隶属度构建的关联矩阵计算问题。综合隶属度通过对目标的归一化残差、速度、航向、AD值等信息综合计算，权向量可通过先验知识或训练进行调整。对关联矩阵计算问题是最优分配的一种特例，因此对关联矩阵采用最优分配策略进行求解，计算量测和航迹配对。仿真结果表明该算法能够大幅度提高群内密集多目标的关联准确性。

[1]Singer R A, Stein J J. An Optimal Tracking Filter for Processing Sensor Data of Imprecisely Determined Origin in Surveillance Systems[C]//Proc. 10thIEEE conf. on Decision & Control, Miami Beach, FL, 1971.12:171-175.

[2]Kuo-Chu Chang , Bar-Shalom Y. A Simplification of the JPDAM Algorithm[J]. IEEE Transactions on Automatic Control,1986(3):989-991.

[3]张成宝. 密集目标环境下的数据关联算法研究[D]. 中国舰船研究院，2013.

[4]俞建国,刘梅,武云丽,高寒松. 基于非对称交互多模型弹道导弹跟踪[J]. 系统工程与电子技术,2010(12).

[5]江宝安. 基于UKF的再入大气层弹道导弹跟踪研究[J]. 雷达科学与技术,2008(2).

[6]张荣涛. 多雷达跟踪弹道导弹交接预报技术研究[J]. 现代雷达,2010(8).

[7]崔彩霞. 智能分类方法[M].北京:气象出版社，2009:130-137.

[8]钮俊清,单奇,任清安,刘军伟. 跟踪弹道导弹全阶段的可变多模型方法[J]. 雷达科学与技术,2011(3).

[9]张峰,息木林,田康生. 基于交互式多模型的弹道导弹跟踪[J]. 导弹与航天运载技术,2011(6).

[10]陈映,文树梁,程臻.一种适用于助推段弹道导弹的跟踪方法研究[J].系统仿真学报,2012(5).

[11]张峰,田康生,息木林. 弹道导弹运动建模与跟踪研究[J]. 弹箭与制导学报,2012(3).

[12]蔡志武,赵东明. UKF滤波器性能分析及其在轨道计算中的仿真试验[J]. 武汉大学学报(信息科学版),2006(2).

A data association algorithm for ballistic missile targets based on optimal allocation strategy

MA Min1,2, JIN Jun-feng1,2

(1.No. 38 Research Institute of CETC, Hefei 230088;2. Aperture Array and Space Detection Key Lab of Anhui Province, Hefei 230088)

During the penetration of ballistic missile targets, there will be lots of baits or dummy warheads forming group targets. Targets with the similar motion characteristics from the same group are so close to each other that it is difficult to track each target continuously and correctly without false data association. Therefore, delayed target recognition and orbit computation, which shorten the time to intercept ballistic missiles, may occur. A data association algorithm is proposed based on the optimal allocation strategy. First, the target association problem is regarded as a special case of the optimal allocation. Then, according to the normalized residuals of targets, speed, heading and AD values, the association probability is calculated and the association cost matrix is built. Finally, the optimum measurement and track matching are calculated by minimizing the association cost matrix. The simulation results show that the algorithm can significantly improve the accuracy of the target association within the same group.

optimal allocation; ballistic missile target tracking; date association; integrative membership

201604-30；

2016-05-20

马敏(1979-)，男，高级工程师，硕士，研究方向：软件工程、雷达数据处理；靳俊峰(1983-)， 男，高级工程师，博士，研究方向：反导雷达数据处理、多源融合。

TP391

A

1009-0401(2016)03-0009-05