基于免疫规划的传感器非线性校正*

卢莉蓉, 牛晓东, 周晋阳△，石春花

(1.长治医学院生物医学工程系，山西 长治 046000；2.长治医学院 物理教研室，山西 长治，046000)

1 引 言

传感器[1]是可以将被测量转换成电量输出的一种器件。传感器在医学仪器的研制和医学实验中占有重要地位。在理想的状态下，传感器的输入输出间呈线性关系，通过对输出量的测量也就知道了输入量的大小。但在实际应用中多数传感器其输出量与输入量之间的关系为非线性的关系。针对这一问题，人们采用了许多办法来对传感器的非线性进行校正。但现阶段的这些校正方法存在着成本高、校正精度差和稳定性差等缺点[2-3]。

进化规划[4](evolutionary programming，EP)是一种随机搜索算法。在进化规划中，不使用交叉、重组之类体现个体之间相互作用的算子，而只采用变异算子，并且大多数情况下使用高斯变异算子，算法简单易行。变异算子是以一定的概率随机地修改个体，有可能变异后的个体还不如父代个体，即出现了退化现象；还有所有实际问题本身都具有一定的特点，如果利用这些特点则会提高求解的速度，但进化规划中没有利用这些特点。以上这两点就影响了算法的运行速度。而且进化规划保持种群多样性的能力不足，易于早熟收敛[5-7]。生物免疫系统[8-9]是机体执行免疫应答及免疫功能的重要系统，它可以识别“自己”和“异己”，迅速清除和消灭异物，确保机体的安全性。生物免疫系统具有可产生多样抗体、自我调节和免疫记忆的功能。

将生物免疫系统的机制应用于进化规划算法中，借鉴免疫系统能产生和维持多样性抗体的能力,以及自我调节能力,在进化算法的整体框架上引入免疫机制,就形成了免疫规划[10](immune programming，IP)。我们研究并应用免疫规划解决传感器系统的非线性校正问题。实例分析的结果表明应用免疫规划对传感器进行非线性校正，不仅可以提高校正精度，速度和稳定性也有了大幅度的提高。

2 校正模型

校正模型见图1。

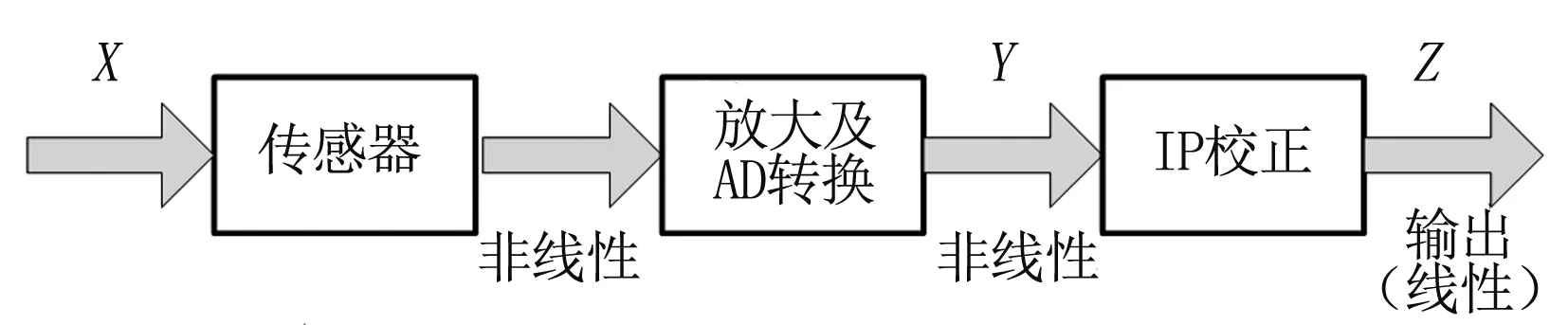
图1 校正模型

图中X是被测量,作为传感器的输入信号。X经过传感器后输出一个非线性信号，再经过放大器和AD转换器后输出Y，Y与X之间依然是呈非线性的，最后经过IP校正输出Z。

IP校正主要就是要进行数据处理和非线性校正，使得最终的输出Z与传感器的输入X之间呈线性关系。

设Y与X之间的关系为Y=f(X)，Z与Y之间的关系为Z=g(Y)，若满足g(Y)=f-1(Y)，则：

Z=g(Y)=f-1(Y)=X

(1)

从(1)式中可以看出, 输出Z与输入X是呈线性关系的，即非线性校正成功。本文的目的就是利用IP来求校正环节Z=g(Y)，即Z=f-1(Y)。

Z可以表示为:

Z=f-1(Y)=a0+a1Y+a2Y2+…+anYn

(2)

式(2)中，a0，a1，a2，…，an为待定系数，n的值一般取3，即:

Z=f-1(Y)=a0+a1Y+a2Y2+a3Y3

(3)

式中，a0，a1，a2，a3为待定系数。只要确定了式(3)中的待定系数，也就确定了校正环节Z=f-1(Y)。

3 利用IP实现传感器非线性校正的步骤

将生物免疫系统的机制应用于进化规划算法中，就形成了免疫规划。IP流程图见图2。

图2 IP流程图

应用IP解决传感器系统的非线性校正问题的步骤如下:

(1)抗原的识别。抗原就是对应于我们要求解的问题。抗原的识别就是要找出对应问题的目标函数形式。在本文中，传感器非线性校正的目标函数为：

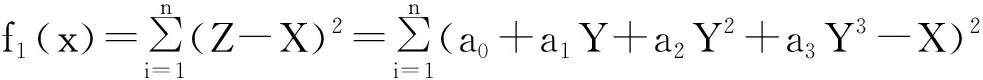
(4)

(2)初始抗体的产生。通过计算机随机产生随机N+m个个体，这些个体作为初始种群。并将其中的m个个体放入记忆库中。

(3)个体适应度评价。个体适应度由下式来确定:

(5)

(4)高斯变异。在IP中大多采用高斯变异算子。在变异过程中，计算每个个体适应度函数值的线性平方根获得该个体变异的标准差，将每个分量加上一个服从正态分布的随机数。

假设X为个体,σ为高斯变异的标准差。染色体个体有L个基因位。则(X，σ)=((x1，x2，…，xL)，σ) 。经过高斯变异后，

xi(t+1)=xi(t)+N(0，σ(t+1))

(6)

式中，

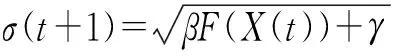
(7)

式中，N(0，σ(t+1))表示均值为0,方差为σ(t+1)的符合正态分布的随机变量；F(X(t))表示当前个体的适应度；系数β、γ为特定的系数，通常取β和γ的值为1和0。

(5)计算个体的适应度和抗体的浓度。计算的对象为高斯变异产生的N个新个体与记忆库中m个个体。

a、计算个体的适应度。依据公式(5)即可求得。

b、计算抗体的浓度。对于抗体和b来说，令这两个抗体总的基因位数为L，相同的基因位数为k,并提前设定一常数T=0.5。

我们定义抗体的浓度为：

(8)

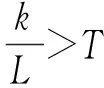
(6)条件判断。判断是否满足终止条件，是则结束，输出结果；否则继续。

(7)形成新的父代种群。新的父代种群的形成是依据个体的期望繁殖概率。简化的个体的期望繁殖概率可用下式计算[11]

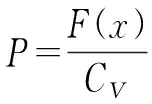
(9)

由式(9)可以看出。F(x)越高,则P越大;CV越大,则P越小。也就是说，我们希望适应度高，并且浓度低的个体繁殖。从而保持了种群的多样性。

按照个体的期望繁殖概率由大到小排列，前N个就构成了新的父代种群。前m个个体就构成了新的记忆库。

(8)新的抗体的产生。通过选择操作来产生新的抗体，选择操作选用轮盘赌选择，个体被选择的概率即为式(9)计算出的个体的期望繁殖概率。

(9)转去执行步骤(3)。

4 实例分析

为了验证本研究所提出方法的先进性，我们在MATLAB上做了大量的仿真实验。其输入、输出数据取自文献[2]的浓度传感器。表1中f为传感器的输出，Cp为传感器的输入：

表1 传感器输出f及对应的实际输入浓度值Cp

从表中可以看出，其输出f与对应的实际输入浓度Cp是呈非线性关系的。这里就要在传感器的输出后加入非线性校正环节，使得最终的输出与输入间呈线性关系。

校正环节：

其中fmax=2500 Hz，a0，a1，a2，a3为待定系数。本研究就是要利用IP来确定这个非线性校正环节多项式的系数。我们取迭代次数为100，a0，a1，a2，a3的位数为20，群体个体为50，记忆库大小为10。

运行IP，结果如下：

图3为实际输入的浓度值与IP拟合曲线的对比值。圆圈代表的是对应于实际输入浓度的实际输出频率。实线代表的是对应于非线性校正环节实际输入频率的非校正环节的输出。从图3可看出：对应于相同的频率来说，实际的输入浓度值与经过非线性校正后的输出值基本上是相同的，也就是整个浓度传感器系统的输入输出基本相同，从而实现了线性输出，实现了浓度传感器的非线性校正。

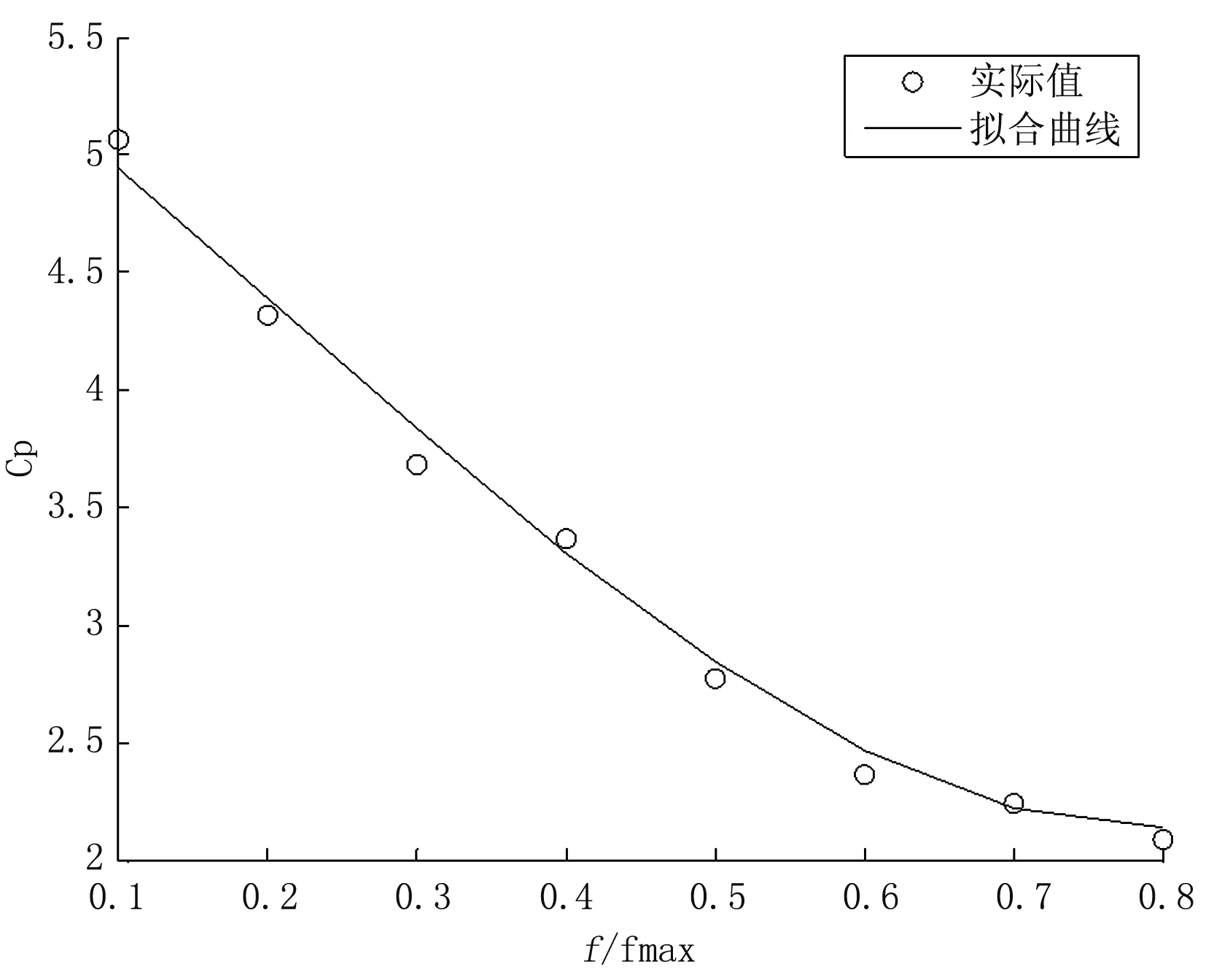
图3 实际值与IP拟合曲线

图4是利用IP对浓度传感器进行非线性校正经过100次迭代后最优解变化图，横轴代表的是进化代数，纵轴代表的是目标函数值(即(4)式)的变化，目标函数值越小，非线性校正的效果就越好。从图4中可看出种群经过58代进化后收敛到目标函数最小值。目标函数最小值为0.0635，并且可得到待定系数为：

a0=5.4478，a1=-4.8007，a2=-3.5829，a3=5.5091

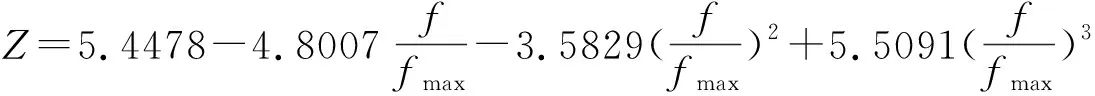
图4 经过100次迭代后目标函数值的变化

利用IP对此浓度传感器进行传感器的非线性校正，运行100次，将运行结果与文献[2]中的结果进行比较，结果见表2。

表2 IP与IGA的运行结果比较

实例分析可看出，利用IP对传感器进行传感器的非线性校正，整个浓度传感器的输入与输出基本相同，目标函数值可以达到0.0635，比利用IGA对传感器进行非线性校正的目标函数值0.3477大大减小，说明此校正方法具有较高的校正精度；而且从图4还可以看出曲线在58代就收敛到了目标函数的最小值，说明此校正方法具有较快的收敛速度；运行程序100次，95%都可收敛到了目标函数的最小值，说明此校正方法具有非常好的稳定性。

5 结论

传感器作为医学测量中的核心部件，其精度和稳定性决定了医学测量的精度和稳定性。但是大多数传感器所存在的输入输出呈非线性的特点，这给医学仪器的测量带来了很多不便。本研究在进化规划的基础上引入生物免疫机制，从而形成免疫规划，利用免疫规划来计算得到校正环节的待定常数，同时使得整个系统的输出与传感器的输入间呈线性关系，即对传感器实现了非线性校正。实践表明, 利用免疫规划对传感器进行传感器的非线性校正，具有较高的校正精度，较快的收敛速度和非常好的稳定性。