Numerical investigation of flow and heat transfer performances of horizontal spiral-coil pipes*

Jia-dong JI （季家东）， Pei-qi GE （葛培琪），2， Wen-bo BI （毕文波）

1. School of Mechanical Engineering， Shandong University， Jinan 250061， China， E-mail: jjd1006@163.com

2.Key Laboratory of High Efficiency and Clean Mechanical Manufacture of Ministry of Education， Shandong University， Jinan 250061， China



Numerical investigation of flow and heat transfer performances of horizontal spiral-coil pipes*

Jia-dong JI （季家东）1， Pei-qi GE （葛培琪）1，2， Wen-bo BI （毕文波）1

1. School of Mechanical Engineering， Shandong University， Jinan 250061， China， E-mail: jjd1006@163.com

2.Key Laboratory of High Efficiency and Clean Mechanical Manufacture of Ministry of Education， Shandong University， Jinan 250061， China

The flow and heat transfer performances of horizontal spiral-coil pipes of circular and elliptical cross-sections are studied. The numerical results are compared with the experimental data， to verify the numerical method. The effects of the inlet water mass flow rate， the structural parameters， the helical pitch and the radius ratio on the heat transfer performances are investigated. Performances of the secondary fluid flow with different radius ratios are also investigated. Numerical results demonstrate that the heat transfer coefficient and the Nusselt number increase with the increase of the water mass flow rate or the helical pitch. The maximum heat transfer coefficient and the maximum Nusselt number are obtained when the radius ratio is equal to 1.00. In addition， the fluid particle moves spirally along the pipe and the velocity changes periodically. The particle flow intensity and the spiral movement frequency decrease significantly with the increase of the radius ratio. Besides， the secondary flow profile in the horizontal spiral-coil pipe contains two oppositely rotating eddies， and the eddy intensity decreases significantly along the pipe owing to the change of curvature. The decreasing tendency of the eddy intensity along the pipe increases with the increase of the radius ratio.

heat exchanger， horizontal spiral-coil pipe， heat transfer performance， flow performance， secondary fluid flow

Introduction

The spiral-coil pipes are most widely applied in several heat transfer fields， such as refrigeration systems， chemical reactors and heat exchangers. This type of pipes can induce the generation of the centrifugal force， which is beneficial to the production of a secondary flow， to affect the flow field and the heat transfer significantly［1-3］. Dean （1928） proposed a mathematical model for the fluid flow in a curved pipe with a constant radius. It was revealed that the secondary flow could be developed in coiled pipes when a parameter （Dean number） was larger than a certain critical value. In order to investigate the flow and heat transfer performances in spiral-coil pipes， numerous numerical［4-7］and experimental［8-13］studies were carried out. However， most of the studies of spiral-coil pipes focused on dimensional spiral-coil pipes and dimensional spiral-coil pipe heat exchangers.

There are only a few studies of the flow and heat transfer performances of the horizontal spiral-coil pipes. Kurnia et al.［14］studied the flow and heat transfer performances of three types of spiral-coil square pipes with laminar non-Newtonian fluids in them. The results indicate that the horizontal spiral-coil pipes enjoy a good performance as compared with conical spiral-coil pipes and other spiral-coil pipes. Naphon and Suwagrai［15，16］investigated the heat transfer performances of the horizontal spiral-coil pipes with different curvature ratios. The results reveal that the performances of the heat transfer are influenced by the centrifugal force significantly. In addition， the heat transfer coefficient obtained from the horizontal spiral-coil pipes is higher than that obtained from the straight pipe of an equivalent pipe length. Altaç and Altun［17］investigated the effects of the Prandtl number，the Dean number， the curvature ratio and the helicalpitch on the heat transfer and the friction factor of the horizontal spiral-coil pipes. The results indicate that the heat transfer is increased about 2-4 times with the increase of the Reynolds number due to the secondary flow and the centrifugal forces. Furthermore， Naphon and Wongwises［18-21］investigated the heat transfer characteristics of the horizontal spirally coiled heat exchanger and the horizontal spirally coiled finnedtube heat exchanger under different conditions. Air and water were used as working fluids in the shellside and the tube-side. The results reveal that the heat transfer rate is directly related to the inlet mass flow rate of the shell-side and tube-side fluids， and the inlet temperatures of the shell-side and tube-side fluids.

Compared with dimensional spiral-coil pipes， the horizontal spiral-coil pipes have a more compact structure and occupy less space in heat exchangers. In addition， the compact structure has important implications for improving the heat transfer efficiency per unit space in heat exchangers. The present work is to investigate the flow and heat transfer performances of the horizontal spiral-coil pipes of circular and elliptical cross-sections using a numerical method. The research can help the study of the mechanism of the heat transfer enhancement， the optimization of the pipe structure and the improvement of the exchanger.

Fig.1 The geometry and coordinate system of the horizontal spiral-coil pipe

1. Mathematical model

Figure 1 shows the structure and the coordinate system of a horizontal spiral-coil pipe， where Roand Riare the outermost and innermost spiral-coil pipe radii， respectively，H is the helical pitch，ϕis the polar angle，θis the circumferential angle， anda andb are the horizontal and vertical radii of the elliptical pipe cross-section， respectively. The horizontal spiral-coil pipe is described by the polar equation R（ϕ）=Ri+Hϕ/（2π）.S1and S2are two crosssections of the pipe between the water inlet and the water outlet.

In our study， the outermost radius Roand the pipe cross-section areaA are constant parameters，and the radius ratio b/ a and the helical pitchH are variable parameters. Table 1 shows the structural parameters of the horizontal spiral-coil pipes in the study.

Table 1 Structural parameters of the horizontal spirally coiled tubes

The steady-state equations of the Newtonian fluids can be expressed as

Continuity equation

Momentum equation

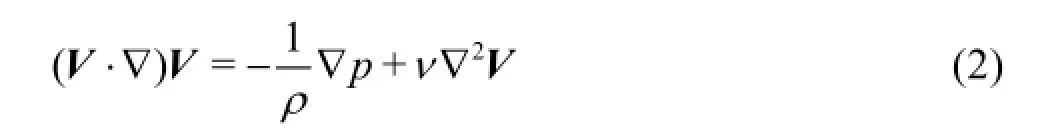
Energy equation

whereV is the fluid velocity，p is the pressure，T is the temperature，νis the kinematic viscosity of the fluid， andαis the thermal diffusivity.

Based on the critical Reynolds number of the helical pipe［3］， the standard k-εturbulence model is used to simulate the flow and heat transfer performances， focusing on the geometry and the physics. The turbulent kinetic energy equation and the turbulent kinetic energy dissipation equation are expressed as

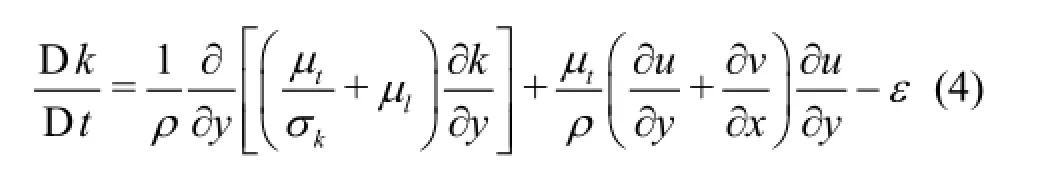
where σkand σεare the diffusion Prandtl numbers，Cµ，Cε1and Cε2， are the turbulent model constants，andµland µtare the viscosities of laminar and turbulent flows， respectively.

In the study， the modified constants of the standard k-εmodel are as follows［15，16］:

Non-slip boundary condition and constant temperature，T=Tw， are employed on the wall of the spiralcoil pipe. Additionally， the following boundary conditions are used at the inlet of the pipe.

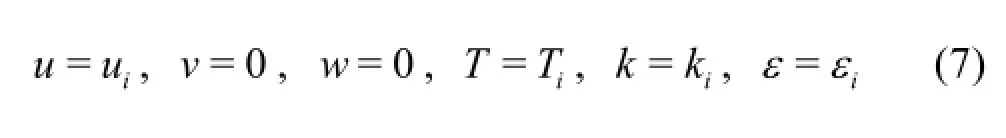
where

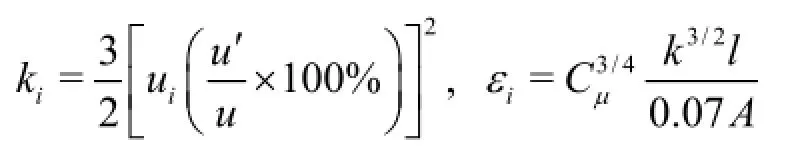
u′is the root-mean-square of the velocity fluctuation，andAandlare the area and the perimeter of the spirally coiled pipe， respectively.

2. Verification of numerical method

Naphon and Suwagrai［15，16］investigated the heat transfer performances of the horizontal spiral-coil pipes of circular cross-section， experimentally. Details of the schematic diagram and the experimental apparatus can be found in the Refs.［15，16］.

Fig.2 The unstructured non-uniform grids system for horizontal spiral-coil pipe

The finite element model of the horizontal spiralcoil pipe is created firstly to test the numerical simulation. According to the experiment， the diameter of the pipe cross-section is 0.008 m， the outermost radius of the spiral-coil pipe is 0.203 m， and the helical pitch of the pipe cross-section is 0.01360 m.

Figure 2 shows the unstructured non-uniform grid system of the fluid domain for the horizontal spiral-coil pipe， which is used to discretize the governing equations mentioned above. Unstructured grids are used to mesh the pipe cross-section， and the sweep method is used to discrete the entire volume of the fluid domain. Moreover， the boundary layers are applied on the fluid domain near the inner wall of the horizontal spiral-coil pipe.

The commercial CFD software Fluent is used as the numerical solver. The mass-flow-inlet boundary condition is imposed at the inlet of the pipe， and the pressure-outlet boundary condition is imposed at the outlet of the pipe. At the inlet， the fluid with temperature，Ti=293.15 K or 298.15 K， enters the horizontal spiral-coil pipes at the mass flow rate ofui=0.05 kg/s. The wall temperature of the pipe is assumed to be constant，Tw=308.15 K. In addition， the SIMPLEC algorithm and the second-order upwind scheme are used to process the pressure-velocity coupling problem based on the control volume method.

The numerical computation ends when the residual values satisfy the following convergence criterion

The numerical results of the total heat transfer rateQ ， for two different inlet water temperatures with different grid strategies， are shown in Table 2.

It can be seen from Table 2 that the numerical results are in an excellent agreement with the experimental data， and the largest relative error is less than 9.5%. The numerical results are slightly higher than the data obtained from the experiment， as is consistent with the result of Naphon and Suwagrai［16］. In addition，it can be noticed that the larger the number of the boundary layers and/or the higher the mesh density，the smaller the difference between the numerical results and the experimental data.

In view of the accuracy and the computational efficiency， the first and last grid strategies are abandoned in the subsequent research due to the low accuracy or the huge time-consumption. The second grid strategy is used in the subsequent research by taking both the accuracy and the computation time intoaccount. During the subsequent research， the flow and heat transfer performances of the horizontal spiral-coil pipes are analyzed based on the numerical results.

Table 2 The simulation results of total heat transfer rate

3. Results and discussions

3.1 Effect of mass flow rate on pipe heat transfer

In order to investigate the effect of the inlet water mass flow rate on the heat transfer performances of the horizontal spiral-coil pipes， numerical simulations are carried out under the condition of the constant pipe wall temperature （Tw=308.15 K）， and different inlet cold water temperatures （Ti=293.15 K and 298.15 K）. The structural parameters of the pipe are kept constant，H =0.03000 m，b/ a =1.00）.

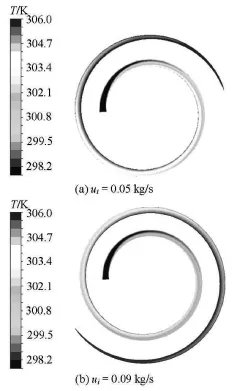
Fig.3 The temperature field contours at different inlet water mass flow rates

The contours of the temperature distribution in the range of 298.15 K to 306.00 K along the horizontal section at different inlet water mass flow rates（0.05 kg/s and 0.09 kg/s） are shown in Fig.3， where，the inlet water temperature Tiis 298.15 K. It can be seen that the thermal entry length at ui=0.05 kg/s is about 1.50 coil， and the thermal entry length at ui= 0.09 kg/s is about 1.90 coil. It indicates that the thermal entry length increases with the increase of the Reynolds number. Due to the curvature， the temperature of the fluid at the inner side of the pipe wall is higher.

Fig.4 Variation of heat transfer rate against the inlet water mass flow rate

Fig.5 Variation of heat transfer coefficient and Nusselt number against the inlet water mass flow rate

Figure 4 shows the variation of the total heat transfer rateQ against the inlet water mass flow rate ui. It can be observed that the total heat transfer rate increases with the increase of the inlet water mass flow rate， and a linear relation is excellently held true within the calculation parameters of this section. The inlet water temperature influences the total heat transfer rate significantly， and the total heat transfer rate is higher when the inlet water has a higher temperature at a given water mass flow rate. The conclusions are consistent with the results of Refs.［15，16，19-21］. The effects of the inlet water mass flow rate on the areaweighted average of the heat transfer coefficienth and the area-weighted average of the Nusselt number Nuare illustrated in Fig.5. It can be observed that the heat transfer coefficient and the Nusselt number increase with the increase of the inlet water mass flow rate. The reason is that the heat transfer coefficient and the Nusselt number all depend directly on the heat removal capacity of the water inside the pipe. On the other hand， the inlet water temperature almost has no effects on the heat transfer coefficient and the Nusselt number.

Fig.6 The temperature field contours for different helical pitches

3.2 Effect of structural parameters on pipe heat transfer

The heat transfer performances of horizontal spiral-coil pipes of different helical pitches are investigated. The outermost radius R1=0.203m， the pipe cross-section areaA=50.3× 10-6m2， the radius ratio b/ a =1.00， whereas the helical pitchHvaries from 0.01360 m to 0.03000 m. In addition， the inlet water temperature is 298.15 K， and the wall temperatureTwis 308.15 K.

Figure 6 shows the contours of the temperature distribution in the range of 298.15 K to 306.00 K for different helical pitches，H =0.01770 mand H= 0.02385 m. It can be seen that the thermal entry length for H=0.01770 mis about 0.740 m （0.90 coil）， and the thermal entry length forH=0.02385 mis about 0.680 m （1.15 coil）. It indicates that the thermal entry length decreases with the increase of the helical pitch.

Fig.7 Variation of heat transfer coefficient and area against the helical pitch

Fig.8 Variation of heat transfer coefficient and Nusselt number against the helical pitch

Figure 7 shows the variation of the area-weighted average of the heat transfer coefficient and the heat transfer area Ahagainst the helical pitch. It can be seen that the heat transfer coefficient increases with the increase of the helical pitch， while the heat transfer area decreases with the increase of the helical pitch. Apparently， the horizontal spiral-coil pipe has a smaller average curvature radius and a shorter pipe length for a larger helical pitch. The smaller curvature radius is beneficial to the heat transfer process， and this is the reason why the heat transfer coefficient increases with the increase of the helical pitch. Figure 8 shows the variation of the total heat transfer rate and the area-weighted average of Nusselt number against the helical pitch. It can be seen that the Nusselt number increases with the increase of the helical pitch. On the other hand， the helical pitch has a negligible influence on the total heat transfer rate.

The heat transfer performances of the horizontal spiral-coil pipes of elliptic cross-sections are also investigated. The numerical simulations are carried out under the conditions of constant pipe wall temperature（Tw=308.15 K）， and constant inlet water temperature（Ti=298.15 K）. In addition， the outermost radius Ro=0.203m， the area of the pipe cross-section A= 50.3×10-6m2， the helical pitch H=0.03000 m，whereas the radius ratio（b/ a）varies from 0.50 to 2.00.

Fig.9 The temperature field contours for different radius ratios

Figure 9 shows the contours of the temperature distribution in the range of 298.15 K to 306.0 K for different radius ratios，b/ a =0.50and b/ a=2.00. It can be seen that the thermal entry length forb/ a= 0.50 is slightly shorter than that for b/ a=2.00，however， the two types of pipes have the same heat transfer area. It indicates that the heat transfer performance of the horizontal spiral-coil pipe forb/ a=0.50 is slightly better than that forb/ a=2.00. Compared with Fig.3（a）， the thermal entry lengths of the two types of pipes calculated in this section are less than that of the pipes of circular cross-section， as showed in Fig.3（a）. More interestingly， the thermal entry length increases with the increase of the radius ratio whenb/ a＜1.00， and decreases with the increase of the radius ratio when b/ a＞1.00.

Fig.10 Variation of heat transfer coefficient and area against the radius ratio

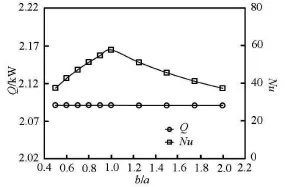
Fig.11 Variation of heat transfer coefficient and Nusselt number against the radius ratio

The variations of the area-weighted average of the heat transfer coefficient and the heat transfer area against the radius ratioare shown in Fig.10. It can be seen that the heat transfer coefficient increases with the increase of the radius ratio when b/ a＜1.00， and decreases with the increase of the radius ratio when b/ a＜1.00. The variation of the heat transfer area is in an opposite trend of that of the heat transfer coefficient. Apparently， the heat transfer coefficient reaches the maximum whenb/ a=1.00， corresponding to the pipe of circular cross-section. For pipes of the same cross-sectional shape， for instance，b/ a =0.50and b/ a=2.00， the heat transfer coefficient of the former pipe is slightly larger than that of the latter. The variations of the total heat transfer rate and the areaweighted average of the Nusselt number against the radius ratios are shown in Fig.11. It can be seen that the variation of the Nusselt number against the radius ratio is similar to that of the heat transfer coefficient. Moreover， the radius ratio has a negligible influence on the total heat transfer rate. Generally speaking， for pipes of the same cross-sectional shape， the heat transfer of pipes withb/ a＜1.00is slightly better than that withb/ a＞1.00.

3.3 The fluid flow in the horizontal spiral-coil pipe

The fluid flow in the horizontal spiral-coil pipe，especially， the generation and the evolution of the secondary fluid flow， has a significant influence on the enhancement of the heat transfer. The analyses of the fluid flow in the pipe of different curvature radii along the horizontal spiral-coil pipe are important. During the following simulation， the outermost radius Ro=0.203m， the pipe cross-section area A=50.3× 10-6m2， and the helical pitch H=0.03000 m. Moreover， the inlet cold water temperatureTi=298.15 K，and the wall temperature（Tw=308.15 K）.

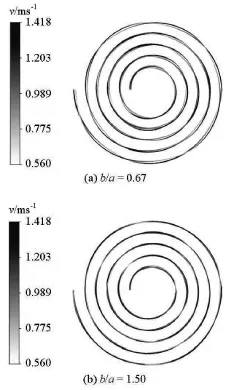
Fig.12 The streamline distributions of the fluid field for different radius ratios

Streamline distributions of the fluid field along the horizontal spiral-coil pipe for different radius ratios，b/ a =0.67and b/ a=1.50， are shown in Fig.12. Three fluid particles are applied for easy observation. It can be seen that the fluid particles move spirally along the pipe， and the velocities of the fluid particles change periodically. Apparently， compared with the velocity of the fluid particle near the inside of the pipe wall， the velocity is higher when the fluid particle is near the outside of the pipe wall. On the other hand， the particle flow intensity and the spiral movement frequency decrease significantly with the increase of the radius ratio.

The velocity vectors of the secondary fluid flow on two cross-sections of the horizontal spiral-coil pipe of circular cross-section（b/ a=1.00）are shown in Fig.13. The left side of the vector diagram indicates the inner of the pipe， and the right side of the vector diagram refers to the outer of the pipe. It can be observed that the secondary fluid flow is generated when the water flows through the horizontal spiralcoil pipe， owing to the curvature of the pipe. The secondary fluid flow field on cross-section S1involves larger velocities than the second fluid flow on cross-sectionS2. The largest velocities are 0.149 m/s and 0.079 m/s on cross-sections S1and S2， respectively. Approximately， the largest velocity on crosssectionS1is 1.90 times larger than that on crosssection S2. In addition， the secondary fluid flow profile of the horizontal spiral-coil pipe contains two oppositely rotating eddies. It can be observed that the eddy intensity decreases significantly along the pipe owing to the change of curvature.

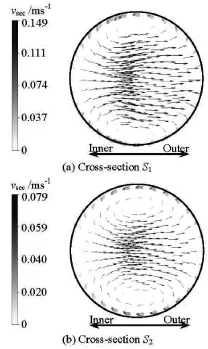
Fig.13 The secondary fluid flow in the horizontal spiral-coil pipe （b/ a=1.00）

Figure 14 and Fig.15 show the velocity vectors of the secondary fluid flow on two cross-sections of the horizontal spiral-coil pipe of elliptical cross-sections（b/ a =0.67and b/ a=1.50）. It can be noticed that the fields of the secondary fluid flow in the pipes of elliptical cross-sections are similar to those in the pipes of circular cross-section. The largest velocity on cross-sectionS1is 0.156 m/s， and on cross-section S2the largest velocity is 0.094 m/s when the radius ratio is equal to 0.67. The largest velocity on crosssectionS1is about 1.66 times larger than that on cross-section S2. Similarly， the largest velocities are 0.140 m/s， and 0.067 m/s on cross-sections S1and S2， respectively， when the radius ratio is equal to 1.50.

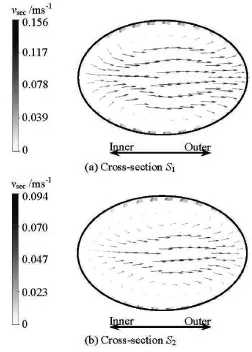
Fig.14 The secondary fluid flow in the horizontal spiral-coil pipe （b/ a=0.67）

Fig.15 The secondary fluid flow in the horizontal spiral-coil pipe （b/ a=1.50）

The largest velocity on cross-section S1is about 2.10 times larger than that on cross-sectionS2. From Fig.13， Fig.14 and Fig.15， it is clearly seen that the decreasing tendency of the eddy intensity along the pipe increases with the increase of the radius ratio. Additionally， it can be clearly observed that the largest velocity on cross-sectionS1of b/ a=0.67is about 1.05 times larger than that on the cross-section of b/ a =1.00， as shown in Fig.13（a）， and about 1.11 times larger than that on the cross-section of b/ a=1.50. It indicates that the eddy intensity decreases with the increase of the radius ratio.

4. Conclusions

The flow and heat transfer performances of the horizontal spiral-coil pipes of circular and elliptical cross-sections are investigated numerically. Compared the numerical results with the experimental data， the numerical method is verified. The effects of the mass flow rate， the structural parameters， the helical pitch H and the radius ratio b/ a， on the heat transfer performances are discussed. The secondary fluid flow performances on two cross-sections of different radius ratios，b/ a =0.67，b/ a =1.00and b/ a=1.50， are also investigated.

（1） Simulation results of different inlet water temperatures with different grid strategies are in an excellent agreement with the experimental data， and the largest relative error is less than 9.5%. With a due consideration of the accuracy and the computational efficiency， an appropriate grid strategy is employed.

（2） The thermal entry length increases with the increase of the inlet water mass flow rate. Due to the curvature， the temperature of the fluid at the inner side of the pipe wall is higher. Additionally， the total heat transfer rate， the Nusselt number and the heat transfer coefficient are proportional to the inlet water mass flow rate. Moreover， the inlet water temperature influences the total heat transfer rate significantly.

（3） The thermal entry length decreases with the increase of the helical pitch. Additionally， the thermal entry length increases with the increase of the radius ratio when b/ a＜1.00， and decreases with the increase of the radius ratio whenb/ a＞1.00. The heat transfer coefficient and the Nusselt number increase with the increase of the helical pitch. The largest heat transfer coefficient and the largest Nusselt number can be obtained when the radius ratiob/ a=1.00. Moreover，the helical pitch and the radius ratio have minor effects on the total heat transfer rate. More interestingly，for pipes of the same cross-sectional shape， the heat transfer of the pipe of the section withb/ a＜1.00is slightly better than that withb/ a＞1.00.

（4） The fluid particle moves spirally along the horizontal spiral-coil pipe and the velocity changes periodically. Additionally， compared with the velocity of the fluid particle near the inside of the pipe wall，the velocity is higher when the fluid particle is near the outside of the pipe wall. On the other hand， the particle flow intensity and the spiral movement frequency decrease significantly with the increase of the radius ratio.

（5） The secondary flow profile of the horizontal spiral-coil pipe contains two oppositely rotating eddies，and the eddy intensity decreases significantly along the pipe owing to the change of curvature. The fields of the secondary fluid flow inside the pipes of elliptical cross-sections are similar with those in the pipes of circular cross-section. Additionally， the decreasing tendency of the eddy intensity along the pipe increases with the increase of the radius ratio. Moreover， the eddy intensity decreases with the increase of the radius ratio.

References

［1］ JI Jia-dong， GE Pei-qi and BI Wen-bo. Numerical analysis on combination flow induced vibration responses of elastic tube bundle in heat exchanger［J］. Journal of Xi'an Jiaotong University， 2015， 49（9）: 124-129（in chinese）

［2］ YOO G. J.， CHOI H. K. and DONG W. R. Fluid flow and heat transfer characteristics of spiral coiled tube: Effects of Reynolds number and curvature ratio［J］. Journal of Central South University of Technology， 2012， 19（2）: 471-476.

［3］ YAN Ke， GE Pei-qi and BI Wen-bo et al. Characteristics of fluid-structure interaction of conical spiral tube bundle with FEM［J］. Journal of Hydrodynamics， 2010， 22（1）: 121-128.

［4］ LI Cheng-guang， XUE Wan-yun and HUAI Wen-xin. Effect of vegetation on flow structure and dispersion in strongly curved channels［J］. Journal of Hydrodynamics，2015， 27（2）: 286-291.

［5］ NAPHON P.， WONGWISES S. A review of flow and heat transfer characteristics in curved tubes［J］. Renewable and Sustainable Energy Reviews， 2006， 10（5）: 463- 490.

［6］ ZACHÁR A. Analysis of coiled-tube heat exchangers to improve heat transfer rate with spirally corrugated wall［J］. International Journal of Heat and Mass Transfer，2010， 53（19-20）: 3928-3939.

［7］ JI Jia-dong， GE Pei-qi and BI Wen-bo. Numerical analysis on flow-induced vibration responses of elastic tube bundle［J］. Journal of Vibration and Shock， 2016， 35（6）: 80-84（in chinese）.

［8］ SALIMPOUR M. R. Heat transfer coefficients of shell and coiled tube heat exchangers［J］. Experimental Thermal and Fluid Science， 2009， 33（2）: 203-207.

［9］ MITTAL M. K.， KUMAR R. and GUPTA A. An experimental study of the flow of R-407C in an adiabatic helical capillary tube［J］. International Journal of Refrigeration，2010， 33（4）: 870-847.

［10］ JAMAL-ABAD M. T.， ZAMZAMIAN A. and DEHGHAN M. Experimental studies on the heat transfer and pressure drop characteristics of Cu-water and Al-water nanofluids in a spiral coil［J］. Experimental Thermal and Fluid Science， 2013， 47（5）: 206-212.

［11］ GHOBADI M.， MUZYCHKA Y. S. Effect of entrance region and curvature on heat transfer in mini scale curved tubing at constant wall temperature［J］. International Journal of Heat and Mass Transfer， 2013， 65（5）: 357-365.

［12］ GHOBADI M.， MUZYCHKA Y. S. Fully developed heat transfer in mini scale coiled tubing for constant wall temperature［J］. International Journal of Heat and Mass Transfer， 2014， 72（5）: 87-97.

［13］ LU X.， DU X. P. and ZENG M. et al. Shell-side thermalhydraulic performances of multilayer spiral-wound heat exchangers under different wall thermal boundary conditions［J］. Applied Thermal Engineering， 2014， 70（2）: 1216-1227.

［14］ KURNIA J. C.， SASMITO A. P. and MUJUMDAR A. S. Laminar heat transfer performance of power law fluids in coiled square tube with various configurations［J］. Interna- tional Communications in Heat and Mass Transfer， 2014， 57: 100-108.

［15］ NAPHON P.， SUWAGRAI J. Effect of curvature ratios on the heat transfer and flow developments in the horizontal spirally coiled tubes［J］. International Journal of Heat and Mass Transfer， 2007， 50（3-4）: 444-451.

［16］ NAPHON P. Study on the heat transfer and flow characteristics in a spiral-coil tube［J］. International Communications in Heat and Mass Transfer， 2011， 38（1）: 67-74.

［17］ ALTAÇ Z.， ALTUN Ö. Hydrodynamically and thermally developing laminar flow in spiral coil tubes［J］. International Journal of Thermal Sciences， 2014， 77: 96- 107.

［18］ NAPHON P.， WONGWISES S. A study of the heat transfer characteristics of a compact spiral coil heat exchanger under wet-surface conditions［J］. Experimental Thermal and Fluid Science， 2005， 29（4）: 511-521.

［19］ NAPHON P.， WONGWISES S.Heat transfer characteristics and performance of a spirally coiled heat exchanger under sensible cooling conditions［J］. JSME International Journal-Series B: Fluids and Thermal Engineering， 2006， 48（4）: 810-819.

［20］ NAPHON P.， WONGWISES S. Heat transfer coefficients under dry- and wet-surface conditions for a spirally coiled finned tube heat exchanger［J］. International Communications in Heat and Mass Transfer， 2005， 32（3-4）: 371-385.

［21］ WONGWISES S.， NAPHON P. Heat transfer characteristics of a spirally coiled， finned-tube heat exchanger under dry-surface conditions［J］. Heat Transfer Engineering，2006， 27（1）: 25-34.

10.1016/S1001-6058（16）60661-3

June 28， 2014， Revised November 6， 2014）

* Project supported by the National Natural Science Foundation of China （Grant No. 51475268）， the National Key Basic Research Development Program of China （973 Program， Grant No. 2007CB206903）.

Biography: Jia-dong JI （1982-）， Male， Ph. D.

Pei-qi GE， E-mail: pqge@sdu.edu.cn

2016，28（4）:576-584