Numerical investigation of unsteady cavitating turbulent flows around twisted hydrofoil from the Lagrangian viewpoint*

Huai-yu CHENG （程怀玉）， Xin-ping LONG （龙新平）， Bin JI （季斌）， Ye ZHU （祝叶），Jia-jian ZHOU （周加建）

1. Wuhan University， Wuhan 430072， China

2. Hubei Key Laboratory of Waterjet Theory and New Technology， Wuhan University， Wuhan 430072， China

3. Science and Technology on Water Jet Propulsion Laboratory， Shanghai 200011， China，E-mail: chengiu@whu.edu.cn



Numerical investigation of unsteady cavitating turbulent flows around twisted hydrofoil from the Lagrangian viewpoint*

Huai-yu CHENG （程怀玉）1，2，3， Xin-ping LONG （龙新平）1，2， Bin JI （季斌）1，2，3， Ye ZHU （祝叶）1，Jia-jian ZHOU （周加建）3

1. Wuhan University， Wuhan 430072， China

2. Hubei Key Laboratory of Waterjet Theory and New Technology， Wuhan University， Wuhan 430072， China

3. Science and Technology on Water Jet Propulsion Laboratory， Shanghai 200011， China，E-mail: chengiu@whu.edu.cn

Unsteady cavitating turbulent flow around twisted hydrofoil is simulated with Zwart cavitation model combined with the filter-based density correction model （FBDCM）. Numerical results simulated the entire process of the 3-D cavitation shedding including the re-entrant jet and side-entrant jet dynamics and were compared with the available experimental data. The distribution of finite-time Lyapunov exponent （FTLE） was used to analyze the 3-D behavior of the re-entrant jet from the Lagrangian viewpoint，which shows that it can significantly influence the particle trackers in the attached cavity. Further analysis indicates that the different flow behavior on the suction side with different attack angle can be identified with Lagrangian coherent structures （LCS）. For the area with a large attack angle， the primary shedding modifies the flow pattern on the suction side. With the decrease in attack angle，the attached cavity tends to be steady， and LCS A is close to the upper wall. A further decrease in attack angle eliminates LCS A in the boundary layer. The FTLE distribution also indicates that the decreasing attack angle induces a thinner boundary layer along the foil surface on the suction side.

cavitating flow， twisted hydrofoil， LCS， CFD， cavitation

Introduction

Much attention has been focused on cavitating flow because of its complex flow pattern and usually undesirable influence on hydraulic machinery［1-3］. Numerous related experiments have been reported in recent decades and significantly improved knowledge about cavitating flow， such as the relationship between the re-entrant jet and the steady of cavitating flow［4］. At the same time， numerical simulation technology is attracting increasing interest with its notable success in predicting cavitating flows. Huang et al.［5］used filter-based density correction model （FBDCM） with the Zwart cavitation model to investigate unsteady sheet/cloud cavitating flows. Comparisons with experimental results showed that the method captured many details of the cavitating flows， such as the formation，breakup， shedding， and collapse of cavities. Ji et al.［6］numerically investigated complex cavitating flows around a NACA66 hydrofoil with LES. The cavity shedding was theoretically related to the pressure fluctuations by a simplified one dimensional model and 3-D numerical results agreed well with the experimental results.

To provide an accurate experimental database for the validation of computational methods and contribute to the development guidelines for propeller design，Foeth［7］conducted a series of experiments on the cavitating flow around a twisted hydrofoil， namely， the Delft Twist-11 hydrofoil. Experiments indicated that the re-entrant flow direction was largely dictated by the cavity topology， and the side-entrant jet had a noticeable influence on the behavior of the shedding cycle［8-10］. The unsteady cavitation patterns and their evolution around the Delft twisted hydrofoil were simulated by Ji et al.［11］with PANS model. The numerical results reproduced the 3-D cavity structure well，and the frequency of the cavity shedding agreed well with the experimental observation. Zhao et al.［12］simulated the cavitating flow around a 2-D Clark-Y hydrofoil， and a relatively new technology， the Lagrangian investigations， including Lagrangian Coherent Structures （LCS） and particle trajectory， was applied to describe the 2-D flow patterns and capture substantial circumferential motion. Their work showed that the behaviors of vortex structure in different cavitation developing stages could be described with the distributions of LCSs. The findings demonstrated that LCS was a promising method in the study of cavitating flow also shown by Tseng et al.［3］. However，because of the 3-D characteristic of cavitating flow，the 2-D simulation cannot reproduce the cavitating flow well. As a result， some details may be lost in the analysis of LCS with 2-D numerical data.

Inspired by previous research， this paper numerically investigates the 3-D cavitating flow around the twisted hydrofoil using the Zwart cavitation model combined with FBDCM turbulence model. Lagrangian investigations， including LCS and particle trajectory，were adopted to study the 3-D behavior of cavitating flow.

Lagrangian method has been widely used in flow visualization and its comprehensive introduction can be found in Ref.［13］. The geometric structure of the Delft Twist-11 hydrofoil was introduced in detail by Foeth［7］. In the present paper， the attract angle of the entire foil was set to -2oand the chord Cwas 0.15 m in accordance with the experiment by Foeth［7］.

Only half of the Delft Twist-11 hydrofoil was considered because of its symmetry. The hydrofoil was located in a channel with a length of7C ， a width of C ， and a height of2C . The inlet was at2Cupstream of the hydrofoil， and the inlet velocity was set tou-∞=6.97 m/s. The pressure at the outlet 5C downstream of the origin was determined by the cavitation number. The top， bottom， and side of the channel were set as free slip walls， while the foil surface was set as a non-slip wall. The Zwart cavitation model combined with the FBDCM turbulence model［14］was used in the present simulation. A series of mesh studies was conducted，and findings indicate that the mesh used in the simulation provided a good balance between computational efficiency and accuracy. The cavitation simulation was initialized from steady state results with fully wetted model. Then， the cavitation model combined with FBDCM and the unsteady solver was turned on for the cavitation flow simulation.

The predicted cavity shedding frequency was 27.7 Hz， which was slightly underestimated compared with the measured frequency of 32.2 Hz［7］. Even though some differences exist between the predicted and measured cavitation shedding cycles， the numerical results still predict the cavitation shedding dynamics well.

Fig.1 Comparison of the predicted top views of the iso-surfaces of αv=0.1（left） and the experimental pictures （right）［7］

To show the shedding behavior of cavitation in detail， the time evolution of the predicted cavitating flow is shown by seven snapshots of typical instants in a cycle shown in Fig.1， with the experimental top-view pictures［7］at each instant given for comparison. The numerical cavity shape is depicted by the iso-surface of vapor volume fraction αvwith a value of 0.1. As shown in Fig.1（a）， the attached cavity reached its maximum length with a convex closure， here considered as fully developed. The flow on the sides of the attached cavity is forced into the cavity because of the pressure gradient resulting side-entrant jets. At the closure region， the 3-D shape of the hydrofoil induces the re-entrant jet to radially diverge upstream from the closure at mid-plane. The side-entrant and re-entrant jets both reach the leading edge and collide with the main stream. As a result， the attached cavity is cut off at the leading edge， thereby introducing primary shedding， as shown in Fig.1（b）. The shedding cavity is advected downstream with the main flow and finally collapses， thereby inducing a U-shaped vortex at the rear of the foil and leaving a concave closure line， as shown in Figs.1（c）-1（e）. During this process， the radial divergence of the re-entrant jet is further enhanced because of the concave closure line. The side-entrant and re-entrant jets finally converge， thereby causing secondary shedding， which agrees well with the experimental observation as shown in Fig.1（f）. The secondary shedding is much weaker but modifies the closure line topology to a near-convex shape as Fig.1（g）shows. The topology of the attached cavity grows back to its original convex shape and repeats the process. Thus， the present simulation clearly reproduces the cavitation patterns and their evolution around the Delft Twist-11 hydrofoil and captures the behaviors of the re-entrant flow well and show good agreement with experimental observation.

Fig.2 FTLE field and the time-averaged vorticity distribution in a typical cycle on the symmetry plane

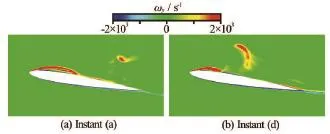
Fig.3 Vorticity distributions on the symmetry plane

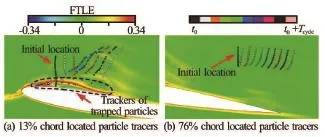
Fig.4 Lagrangian particle's trackers with different initial locations

Figure 2（a） shows the FTLE distribution around the Delft Twist-11 hydrofoil on the symmetry plane. The integral time to calculate the FTLE field is the cavity shedding period from t0to t0+Tcycle， where t0corresponds to the instant （a） in Fig.1 and Tcycleis approximately 0.034 s. Two distinct LCSs， LCS A and LCS B， can be observed at the suction side of hydrofoil and upstream the leading edge shown in Fig.2（a）. Figure 2（b） describes the time-averaged vorticity distribution on the symmetry plane in the same cycle. The flow separation due to the hydrofoil geometric structure is responsible for the formation of LCS B. A reasonable agreement between the FTLE field and the vorticity distribution near the leading edge at the suction side indicates a connection between LCS A and the vorticity distribution. The relatively steady vortex induced by the attached cavity at the leading edge separates the flow into two parts: the particles near the foil are trapped into the vortex， and those far away from the foil surface are advected downstream with the main stream. The separation tendency between the particles of the two parts leads to a relatively high value of FTLE near the interface， thereby resulting in the formation of LCS A. Figure 4（a） shows the particle trackers initially located at 0.133C downstream the leading edge. Most of the particles move downstream in order because of the uniform main stream. The particles near the hydrofoil surface are transported upstream first and then downstream along the vortex boundary as a result of the behavior of the re-entrant jet. Unlike the vortex near the leading edge， the vortex structure near the trailing edge， which is caused by the U-typed vortex that forms from the shedding cavity，does not induce a distinct region with high FTLE. Figure 3 shows the vorticity distributions on the symmetry plane at instant （a） and instant （d）， and indicates that the vortex structure near the trailing edge is unsteady and has little influence on the particle trackers. Figure 4（b） shows the particle trackers initially located near the vortex structure at the trailing edge advected downstream orderly.

Fig.5 FTLE fields on different planes

To qualitatively investigate the 3-D cavitation structure due to the effect of attack angle on the LCS structure， Fig.5 shows the FTLE fields on symmetry plane （y/ C =1.0）， Plane 1（y/ C =0.8）， Plane 2（y/ C =0.6）， and Plane 3（y/ C=0.4）and the corresponding attack angles are9o，7.9o，5.1oand 1.9o， respectively. Considering the expensive computational cost for a 3-D FTLE calculation， the 2-D flow calculating method is adopted on these planes. Three types of flow behavior at the suction side can be identified clearly with LCS: （1） for the area near the symmetry plane with a large attack angle， the attached cavity periodically grows and breaks off corresponding to the primary shedding， which induces distinct flow separation along the interface of liquid and vapor. As shown in Fig.5（a）， the FTLE distribution on the symmetryplane suggests that the cavitating flow near the symmetry plane significantly modifies the local flow pattern not only near the foil surface but also at the entire suction side， （2） with the decrease in the attack angle，the cavitating flow tends to be steady and only small scale shedding， the secondary shedding， can be observed at the rear part of the attached cavity. The region with high FTLE is concentrated on the boundary of the attached cavity， and LCS A is close to the upper wall， （3） for the area with a lower attack angle， the flow is almost fully wetted， and no separation is observed. LCS A vanishes in the boundary layer in correspondence to this condition. The particles near the hydrofoil pass smoothly along the foil surface. A comparison of the distributions of FTLE on Plane 2 and Plane 3 shows a decrease in the boundary layer thickness with a decreasing attack angle.

The cavitating flow around Delft twisted hydrofoil was simulated with Zwart cavitation model combined with the FBDCM turbulence model and analyzed with LCS and particle trajectory from the Lagrangian viewpoint. The main conclusions are as follows:

（1） The Zwart cavitation model combined with the FBDCM turbulence model can accurately capture the flow features in cavitating flows around Delft twisted hydrofoil with reasonable cost. The predicted cavitation evolution agrees well with the experimental results.

（2） Two distinct LCSs， namely， LCS A and LCS B， are observed at the suction side of the hydrofoil and upstream the leading edge， respectively. The main contributor to the formation of LCS A is the relatively steady vortex near the leading edge， and LCS B is induced by the flow separation because of the geometric structure of hydrofoil. The particle trackers show that the behavior of the re-entrant jet significantly affects the flow in the attached cavity.

（3） Three types of flow behavior at the suction side can be identified clearly with LCS. For the area with a large attack angle， the FTLE distribution shows that the cavitating flow， especially the primary shedding， modifies the flow pattern on the suction side，with the decrease in attack angle， the attached cavity tends to be steady， and LCS A is close to the upper wall， a further decrease in attack angle causes LCS A to disappear in the boundary layer. The FTLE distribution also indicates that the decreasing attack angle induces a thinner boundary layer along the foil surface on the suction side.

The 2-D flow calculating method adopted in present paper provides the particle trackers on the symmetry plane and some qualitative conclusions. However， due to the 3-D characteristics of cavitation， it cannot reproduce the behavior of cavitating flow with high accuracy， while the expensive cost for 3-D FTLE calculation method hinders its application in practice. A FTLE calculation method for 3-D flow with reasonnable costs and good accuracies is urgently needed and the relevant work is in progress in our team.

References

［1］ LUO Xian-wu， JI Bin and TSUJIMOTO Yoshinobu. A review of cavitation in hydraulic machinery［J］. Journal of Hydrodynamics， 2016， 28（3）: 335-358.

［2］ KRAVTSOVA A. Y.， MARKOVICH D. M. and PERVUNIN K. S. et al. High-speed visualization and PIV measurements of cavitating flows around a semi-circular leading-edge flat plate and NACA0015 hydrofoil［J］. International Journal of Multiphase Flow， 2014， 60（2）: 119-134.

［3］ TSENG C. C.， LIU P. B. Dynamic behaviors pf the turbulent cavitating flows based on the Eulerian and Lagrangian view points［J］. International Journal of Heat and Mass Transfer， 2016， 102: 479-500.

［4］ KAWANAMI Y.， KATO H. and YAMAGUCHI H. et al. Mechanism and control of cloud cavitation［J］. Journal of Fluids Engineering， 1997， 119（4）: 788-794.

［5］ HUANG B.， YOUNG Y. L. and WANG G. et al. Combined experimental and computational investigation of unsteady structure of sheet/cloud cavitation［J］. Journal of Fluids Engineering， 2013， 135（7）: 071301.

［6］ JI B.， LUO X. and ARNDT R. E. A. et al. Large eddy simulation and theoretical investigations of the transient cavitating vortical flow structure around a NACA66 hydrofoil［J］. International Journal of Multiphase Flow，2015， 68: 121-134.

［7］ FOETH E. J. The structure of three-dimensional sheet cavitation［R］. Delft， The Netherlands: Delft University of Technology， 2008.

［8］ FOETH E. J.， Van DOORNE C. W. H. and Van TERWISGA T. et al. Time resolved PIV and flow visualization of 3D sheet cavitation［J］. Experiments in Fluids，2006， 40（4）: 503-513.

［9］ PENG X. X.， JI B. and CAO Y. et al. Combined experimental observation and numerical simulation of the cloud cavitation with U-type flow structures on hydrofoils［J］. International Journal of Multiphase Flow， 2016， 79: 10-22.

［10］ WU X. C.， WANG Y. W. and HUANG C. G. Effect of mesh resolution on large eddy simulation of cloud cavitating flow around a three dimensional twisted hydrofoil［J］. European Journal of Mechanics-B/Fluids， 2015， 55（1）: 229-240.

［11］ JI B.， LUO X. and WU Y. et al. Numerical analysis of unsteady cavitating turbulent flow and shedding horse-shoe vortex structure around a twisted hydrofoil［J］. International Journal of Multiphase Flow， 2013， 51（5）: 33-43.

［12］ ZHAO Y.， WANG G. and HUANG B. et al. Lagrangian investigations of vortex dynamics in time-dependent cloud cavitating flows［J］. International Journal of Heat and Mass Transfer， 2016， 93: 167-174.

［13］ HALLER G. Lagrangian structures and the rate of strain in a partition of two-dimensional turbulence［J］. Physics of Fluids， 2001， 13（11）: 3365-3385.

［14］ HUANG Biao， WANG Guo-yu and ZHAO Yu. Numerical simulation unsteady cloud cavitating flow with a filterbased density correction model［J］. Journal of Hydrodynamics， 2014， 26（1）: 26-36.

10.1016/S1001-6058（16）60674-1

August 1， 2016， Revised August 8， 2016）

* Project supported by the National Natural Science Foundation of China （Grant Nos. 51576143， 11472197） and Science and Technology on Water Jet Propulsion Laboratory （Grant No. 61422230101162223002）.

Biography: Huai-yu CHENG （1993-）， Male， Ph. D. Candidate

Bin JI， E-mail: jibin@whu.edu.cn

2016，28（4）:709-712