技术创新项目群资源配置模型

2016-10-18戴维序吴伟伟孔宝红

系统工程与电子技术 2016年10期

关键词：效用函数子项目工期

戴维序, 吴伟伟, 于　渤, 孔宝红

(1.哈尔滨工业大学管理学院, 黑龙江哈尔滨 150001; 2. 北京空间飞行器总体设计部, 北京 100094)

技术创新项目群资源配置模型

戴维序1,2, 吴伟伟1, 于渤1, 孔宝红1

(1.哈尔滨工业大学管理学院, 黑龙江哈尔滨 150001; 2. 北京空间飞行器总体设计部, 北京 100094)

为解决技术创新项目群的资源分配问题,首先以研发人员为主要资源,分析了技术创新项目群资源配置的步骤和假设条件,然后提出以时间目标、成本目标和质量目标作为约束条件,构建了以时间、成本和质量为变量的多属性效用函数。在此基础上,以多项目间的时间、成本和质量的综合优化为目的,建立了技术创新项目群资源配置的数学规划模型。最后通过技术创新项目群实例验证了该模型的有效性,可以为国防技术创新项目资源配置提供决策支持。

技术创新; 项目群; 资源配置; 规划模型

0　引　言

当今社会,不断加强的全球化发展趋势、迅猛的经济发展以及不断更新换代的科学技术,使得国防工业尤其是航天企业面临着巨大的发展压力与挑战。面对时间的约束,企业需要在同一个时间段内完成多个技术创新项目,因此必须采用集群管理的方式对技术创新项目进行管理,才能完成预设的技术创新目标。在项目群管理的情况下,企业所面对的管理工作变得更加复杂且难度倍增,尤其是其中的资源管理工作变得极具挑战。文献[1]发现“资源缺乏及无效配置”在各种影响项目群成功的重要因素中占25%,排在第二。因此,实现对项目群资源的最优化配置是最终完成整个项目群目标的关键。

当前,企业在技术创新项目群资源调配工作中存在两个主要问题:一方面,同时实施多个技术创新项目使得资源的调动变得更加复杂和频繁;另一方面,关键路径法及计划评审技术等传统的项目管理工具仅适用于单个项目的管理工作,如果从企业整体项目群层面来考虑资源的调动,那些项目管理工具计划能力不强,不能满足项目群资源调配工作的需要,造成项目群无法达到全部的预期目标。

各个技术创新项目的同时开展必然使得企业中人力资源、设备资源、资金资源和时间资源等各种资源存在共享,由此造成各个项目间发生资源的争夺。因此，怎样使得技术创新项目群的资源得到有效配置成为国内外学者关注的问题。

文献[2]在考虑了项目进展的动态性、资源调度的有效性和在制品及成品库存的情况下,对多项目进展的问题展开了研究,通过对多个项目进行分析和排列组合,求得满足上述3个条件的最短段空闲时间的项目组合安排。文献[3]指出由于项目群中各项目开始和结束日期都受到严格的规定,因此虽然项目群管理具有很大的不确定性,但当项目群中的某个项目未能在规定时间内完成就应该受到惩罚,并根据这种思想提出了项目时间延迟的解决办法。文献[4]给出了在明确项目优先等级的情况下,改进任务列表建立的遗传算法。文献[5]提出了基于排队论的排队资源配置模型,并用实际案例进行了验证。文献[6]基于对学习曲线的认识,对学习曲线进行了深入分析,认为承担相同或相近的工作时间越久,工作的效率会相应的提高,并以此为基础用遗传算法为项目群人力资源配置问题提出了解决方案。文献[7]为多项目情况下人力资源配置遇到的实际问题提出了相对应的分析方法,即极限理论法。文献[8]认为可以通过以下步骤实现对项目群全部资源的统一规划:首先需要确定每个项目的优先级排序,然后识别和确认项目群中的关键资源,最后综合考虑各个子项目的时间进度安排，对资源进行分配。

尽管国内外学者针对资源配置问题提出了多种解决方法,但是,目前的研究对于单个项目的时间、成本和质量这三大目标研究比较多,对于多项目的三大目标的综合优化方面研究还不充分。此外,目前的研究涉及到了工程项目群,但对技术创新项目群的研究还没有充分展开。

本文将研发人员视为技术创新项目群的主要资源,综合考虑完成工期、完成成本和完成质量三大目标,构建基于效用函数的技术创新项目群资源配置模型,并通过实际案例验证该模型对技术创新项目群资源配置优化的有效性。

1　问题分析

1.1问题描述

高科技企业在将技术知识向商业用途转化的过程中,伴随着大量资源投入,因而具有很大风险,这要求技术创新项目群能够实现更大的价值创造。有效地进行资源配置不但能够使得所投入的资源得到高效利用,而且还能有效促进资源价值的实现。技术创新项目群的主要资源包括人力、物力、财力和技术资源。技术研发是具有创造性的工作,而人力资源是所投入的全部资源中最具智慧性、创造性以及能动性的资源,是技术创新活动的载体,能够对其他的投入资源产生配置作用。而企业中物力资源和财力资源的供给对人力资源作用的发挥具有重要影响,是人力资源发挥作用的前提条件,并支撑着人力资源的发展。因此人力资源是技术创新过程中的核心资源,研发人员的分配是技术创新项目群资源配置中的最主要内容。

资源基础观认为稀缺性是企业核心资源的特性之一,尤其是在资源紧缺的情况下,资源配置缺乏规划会导致项目群中的关键项目无法按期完成;而假若资源供给大于需求,会使得项目群内资源累积,造成资源的极大浪费。以上两种情况都无法使得资源的效用得到有效发挥,进而影响项目群整体目标的实现。基于以上考虑,可以根据以下4个阶段对技术创新项目群资源进行配置:

(1) 项目群负责人从整体视角出发,估计出为完成各个子项目需要开展的任务以及预期的完成工期,据此明确完成各个子项目的资源需求,并制定各个子项目的实施方案。

(2) 确定资源限制条件。首先需要明确企业所能提供的全部资源数量,其次结合企业所拥有的资源数量和编制的资源调配计划,明确项目群受到的资源限制条件。

(3) 根据企业发展战略要求,确定技术创新项目的优先级排序,对企业发展影响大的项目优先实施。

(4) 优化配置技术创新项目群资源。在企业现有资源的限制下,根据各个子项目的优先级排序及其对资源的需求情况,对现有资源进行合理分配,满足各子项目的需要。

1.2假设条件

假设 1能够对技术创新项目群中各个子项目的优先级进行排序,且控制整个项目群的网络计划图。

假设 2各个子项目的项目活动一经开展,就会被最终完成,不能被项目内其他活动打断。

假设 3项目内所有活动都只有在其紧前活动完成后方能开始,即项目内所有活动间都是开始-结束的关系。

假设 4在项目执行过程中,每个任务都只会用到一种共享的项目群资源(R),且在项目的执行期内,共享资源的总供给量(R*)维持恒定。

假设 5当项目被压缩至赶工时间时,是以消耗更多的资源成本为代价的,在已被压缩到赶工时间的情况下,就无法再压缩。

假设 6在最长和最短工作时间内,项目任务完成消耗的时间成本和资源成本为一次函数关系。

假设 7若某项目任务需要使用共享资源,则该项目任务的完成质量取常数。同时,若项目任务的完成时间是最长工作时间,则完成质量是100%。

假设 8在最长和最短工作时间内,项目任务的完成质量和持续时间为一次函数关系。

1.3约束条件

1.3.1时间约束

技术创新项目群中各个项目岗位能力和个人胜任力都从专业素质、创新能力、职位适应能力及人格特质4个维度来进行综合评分,评分方法可以采用基于三角模糊数的层次分析方法[9-10],得到研发人员相对岗位匹配度矩阵:

(1)

式中,snlij为第i个人员相对第j项任务的匹配度,其值为

(2)

snlij=1时为标准人,此时研发人员的工作能力与任务需求的匹配程度是1。假设标准人单位时间内的工作量为10,则在满足任务要求的情况下,第i个研发人员在任务j上的工作效率(Lij)为

(3)

分配能够满足任务需求的研发人员的时间,求得不同研发人员组合的情况下,完成第j项任务的最优解,研发人员的组合为

(4)

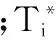
解得完成项目i的工期最短的研发人员组合,此时工期为

(5)

因此,项目群总工期可表示为

(6)

1.3.2成本约束

根据假设5和假设6,任务的直接费用和持续时间之间的关系可表达为

(7)

其中

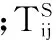
技术创新项目群中第i个项目的成本为

(8)

式中,γij为0-1变量,0表示第i项项目第j项任务使用共享资源,1表示第i项项目第j项任务使用非共享资源；cij为完成项目i中的任务j所消耗的资源成本;Yi表示为完成项目i所消耗的间接成本; Ti表示完成项目i需要的工期。引入γij的原因是:共享资源需要从项目负责人处获取,它不形成子项目的成本费用,却形成整个项目群的成本费用,它的引入可以反映不是共享资源所带来的成本费用变化情况。

在实施技术创新项目群的情况下,不仅需要考虑各个项目的运行成本,还需要将项目群中共享资源的成本情况考虑在内。

(9)

式中,C为技术创新项目群总成本;ci为项目i的成本;ε为共享资源费率;Hij为项目i的第j项任务使用共享资源完成的工作量;A反映项目群实施期间投入的固定成本。

1.3.3质量约束

项目群整体的完成质量最终受到各个任务完成质量的影响,因为项目群是由各个子项目组成的,而子项目的完成又取决于项目中各个任务。任务完成质量为100%,指的是项目的完成情况达到规定要求,表明质量在可容忍的偏差范围之内,此时设为1。由假设7和假设8可知,任务完成质量与时间之间的关系可表达为

(10)

其中

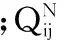
对所得到的Qij进行加权,可得到项目群第i个项目的完成质量,表示为

(11)

其中

式中,ωij为在项目i中第j项任务的权重;Qij为项目i中第j项任务的完成质量;Qi为项目i的完成质量。

因此,项目群总体完成质量为

(12)

式中,Qi为项目群中第i个项目的完成质量;Q为项目群的总体完成质量。

2　模型构建

2.1效用函数

为衡量项目群实施过程中对项目进行管理产生的效益,建立包含工期、成本和质量三大目标的多属性效用函数U(T,C,Q)。以满足工期要求为基础,三变量产生的效益越大越好。

定义 1假设C,Q取不同的数值时,有

(13)

定义 2假设T,C取不同的数值时,有

(14)

而且T,Q取不同的数值时,有

(15)

则工期、成本和质量三变量各自偏好独立[11]。

本文采用二次函数解析法构造工期、成本和质量的效用函数。依据多属性效用理论,多属性各个变量偏好独立为多属性效用函数加式分解性的充要条件,根据多属性效用函数的分解定理[12-13],并基于加式分解性,构建多属性效用函数,可表示为

(16)

式中,U(T)为将工期作为变量的效用函数;θT为工期权重,即工期在三变量中所占比重;U(C)为将成本作为变量的效用函数;θC为成本权重,即成本在三变量中所占比重;U(Q)为将质量作为变量的效用函数;θQ为质量权重,即为质量在三变量中所占比重。可知,θT,θc,θQ≥0, θT+θC+θQ=1。

综合以上条件,构建项目工期T的单属性效用函数为

(17)

项目成本C的单属性效用函数为

(18)

项目质量Q的单属性效用函数为

(19)

式中,Qmin为项目最低完成质量;Qmax为项目最高完成质量;Tmax为项目最长完成工期;Tmin为项目最短完成工期;Cmin为完成项目最低耗费成本;Cmax为完成项目最高耗费成本;a1,a2,a3,a4,a5,a6为相关参数。综上所述,时间、成本和质量的效用函数为

(20)

2.2资源配置模型

模型构建步骤如下:

步骤 1采用摆幅置权法计算各个任务完成质量相对于整个项目完成质量的权重[14-15]。

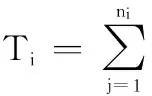
步骤 3计算出为完成各个项目的最小耗费成本和最大耗费成本,及最差完成质量和最佳完成质量。

步骤 4计算出各个项目的三大目标权重(T,C,Q),由此得出各个项目的多属性效用函数。

步骤 5计算出为完成整个项目群所需的总工期、总成本以及总质量的最小值和最大值。

步骤 6计算整个项目群中工期、成本和质量的权重θT,θc,θQ,求得整个项目群的多属性效用函数U(T,C,Q)。

此时,目标函数:

(21)

此模型可根据人岗匹配度将研发人员和工作岗位进行最优组合,并得出整个项目群的最优工期解,确保整个项目群的工期、成本和质量三大目标的效用最大化。

3　实例研究

某国防企业技术创新项目群包含两个相关项目:项目1由8个工作任务组成,项目2由11个工作任务组成。由于资源有限,容易导致资源配置冲突。根据企业类似项目的过往资料,估计出正常及赶工情况下的完成时间和完成质量。同时,还需确定完成项目中各个任务所需的工作量。工作量的计算由任务持续时间和研发人员的工作效率相乘得到,其中任务持续时间用以前企业完成相似项目所需的时间来估计,研发人员工作效率以标准人的工作效率来估计,得到各个任务的工作量。项目的基本数据如表1和表2所示。

表1　项目1的基本数据

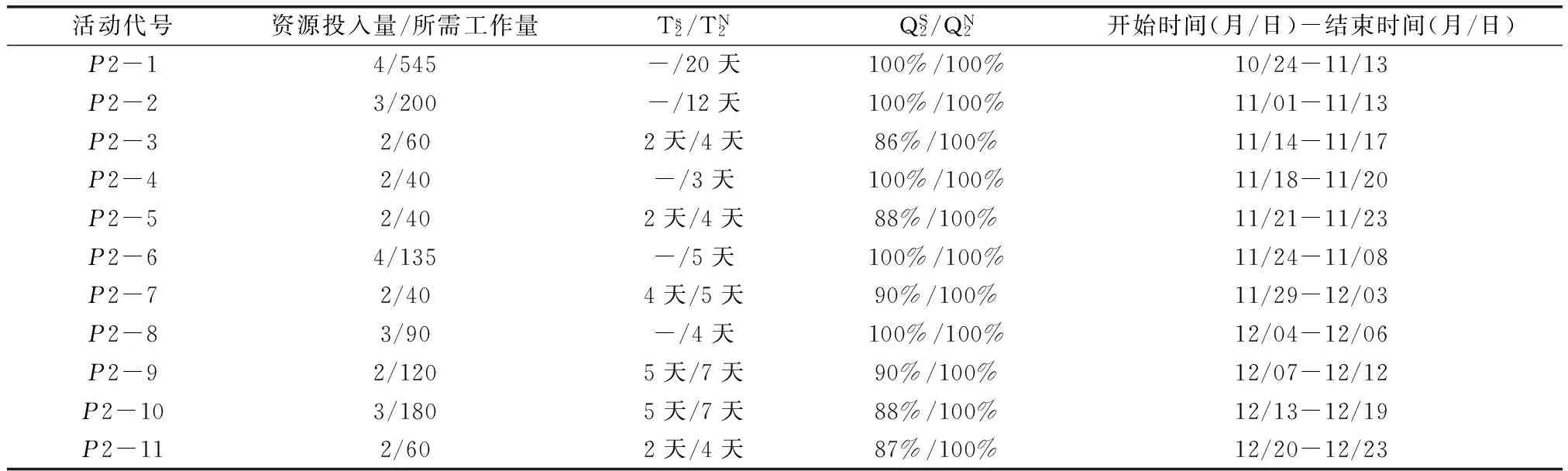
表2　项目2的基本数据

将项目中各个任务的完成质量加权求和得出项目的完成质量。项目中各个任务权重的确定方法为摆幅置权法。据此,得出项目1中P1-1～P1-8各任务的质量权重为(0.167,0.146,0.104,0.063,0.208,0.083,0.188,0.042),以及项目2中P2-1～P2-11各任务的质量权重为(0.149,0.134,0.119,0.112,0.104,0.09,0.082,0.067,0.06,0.045,0.038)。

项目完成的最长工期即为设定的项目最长时间,而项目的最短工期能够由网络计划图中的关键路径获得。此外,在求解整个项目群的最短工期时,应考虑到项目1中的P1-5和项目2中的P2-1、P2-2、P2-4、P2-6和P2-8在同一时间内使用了相同资源,因此需要将满足工作要求的共享资源完全配置到项目1和项目2中。

项目1和项目2的共享资源为12名研发人员,且实际工作中每名研发人员的工作效率有差异。符合项目1P1-5工作要求的研发人员共有9名,根据式(4),则

(22)

求出资源全部利用后的完成最短时间,T15=25。所以有

同理,可以将适合项目1各个任务的工作人员全部用到任务中,得到完成项目的最短时间,即

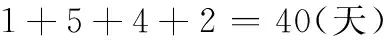
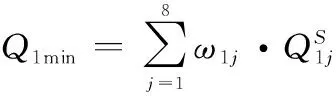
根据工期的最大值和最小值可知,时间越接近于规定时间，范围效用越大,所以项目1工期的效用函数为

(23)

∵ U1(44)=1,U1(78)=0

∴ a11=1,a12=-1/342

(24)

由于任务持续时间越长,完成质量越好,根据项目1的最佳质量和赶工质量的结果,其质量效用函数为

(25)

∵ U1(1)=1,U1(0.915)=0

∴ a13=1,a14=-1/0.0852

(26)

同理,项目2的工期和质量的效用函数为

(27)

(28)

采用摆幅置权法计算工期、成本和质量的权重。由于项目1和项目2只考虑完成工期和质量,而不考虑成本,因此以0计成本的权重。根据计算结果,按照工期和质量进行选择,完成项目1的最佳方案是[44,1],最差方案是[78,0.915],对项目1的完成质量和完成工期进行综合考虑,项目负责人认为最需改进的是完成质量,其次是完成工期,对应的价值偏好分别为100和80,基于此确定项目1的完成工期和完成质量的权重分别为ω1=(0.444,0.556)。同理,项目2完成工期和完成质量的权重分别为ω2=(0.412,0.588)。根据多属性效用函数加式可分解性,构建多属性效用函数的表达式为

(29)

(30)

项目群完成工期可由T=T1+T2得出,因为项目2的开始时间与项目1中P1-5开始时间相同,所以整个项目群的完成工期等于项目1中P1-1～P1-4完成的最短时间加上项目1P1-5～P1-8的完成时间与项目2中P2-1～P2-11完成时间二者中的最大值。可以求得,完成项目群需要的最小工期Tmin=50,需要的最大工期Tmax=79。

项目群完成质量的计算公式为Q=Q1+Q2,计算可知Q∈[1.86,2]。

由前文的结果可以得出,项目群完成的最差方案是(79,1.82),最好方案是(50,2)。项目群负责人对该项目群工期的价值偏好为70,质量的价值偏好为100,求得工期和质量的权重分别为(0.412,0.588)。因此整个项目群的完成工期和完成质量的单效用函数分别为

(31)

(32)

最后,得到项目群的多属性效用函数为

U(T,C,Q)=0.412×[1-1/392(T-40)2]+0.588×[1-1/0.142(Q-2)2]

(33)

在求得项目1、项目2及项目群多属性效用函数的基础上,构建基于人岗匹配度的多层迭代模型

(34)

式中

T=T1+T2,Q=Q1+Q

据此模型可以得出最佳人岗匹配的研发人员分配方案(见表3和表4)和项目中完成每个任务所需的时间(见表5),其中人岗匹配度大于1的为核心研发人员。因此，可以得出项目1的完成工期T1=65.5(天),而项目2的完成工期T2=53(天),整个项目群的完成总工期T=65.5(天),则U(T)=0.572。项目1的质量Q1=0.948,Q2=0.972。项目群的质量Q=1.917,则U(Q)=0.649。项目群的效率U(T,Q)=0.617。如果按照计划分配的资源数量,T=62.5(天),Q=1.,891,则U(T′)=0.667,U(Q′)=0.520,则U(T,Q)=0.507。对比可知,假若按照原有的资源配置计划,不仅在项目群实施过程中,需要分配的研发人员较本文构建的模型需要分配的研发人员数量大,而且会降低项目群的总效用,造成资源的无效利用。综合来看,本文提出的模型具有可操作性。

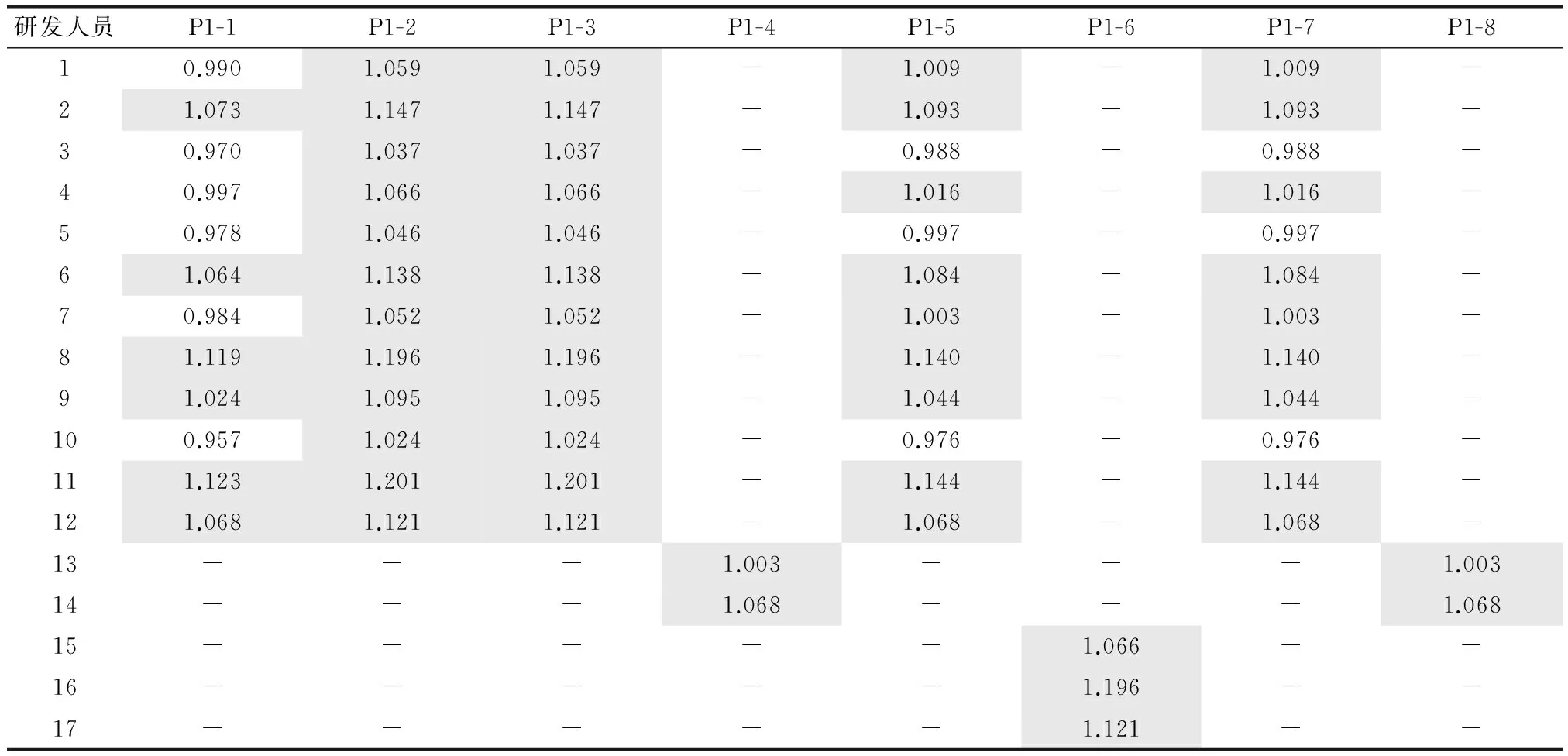
表3　项目1研发人员分配

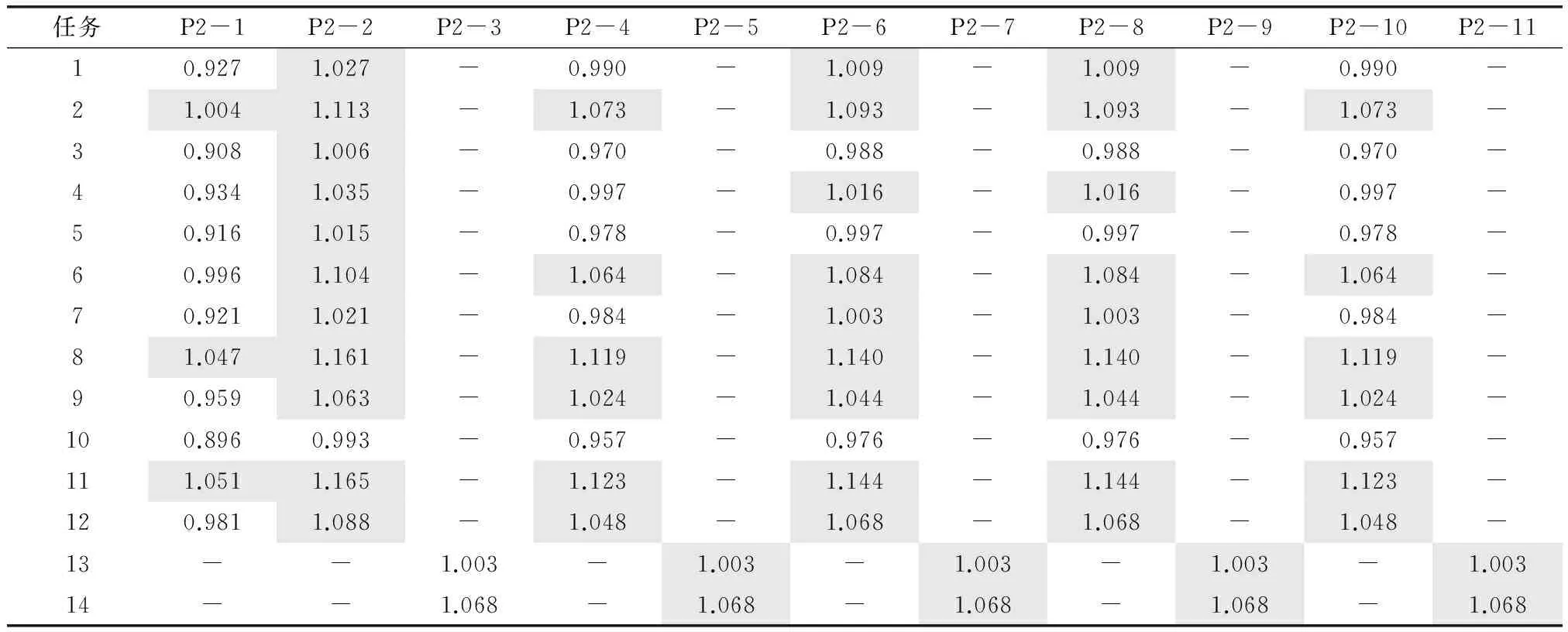
表4　项目2研发人员分配

表5　项目1和项目2各个任务持续时间

4　结　论

在科技飞速发展的当今社会,高技术的开发往往是以技术创新项目群的方式进行,合理分配项目群资源对于成功的技术创新具有重要作用。当前的研究还未能对技术创新项目群资源配置构建有效的定量模型和形成完整具体的支撑方法。本文结合实际背景,综合考虑时间、成本和质量目标,建立了资源配置的数学模型。依据研发人员岗位适合度和工作效率,计算出完成各个项目所需要的时间,并以此为基础,求得各个项目的成本值以及质量值,进而求得总效用函数的最大值。同时通过对企业现实案例的计算,结果显示,本文构建的模型能够对技术创新项目群的资源进行更优配置,具有可行性。

[1] Elonen S, Artto K A. Problems in managing internal development projects in multi-project environments[J].InternationalJournalofProjectManagement, 2003, 21(6): 395-402.

[2] Browning T R, Yassine A A. Resource-constrained multi-project scheduling: priority rule performance revisited[J].InternationalJournalofProductionEconomics, 2010, 126(2): 212-228.

[3] Hans E W, Herroelen W, Leus R, et al. A hierarchical approach to multi-project planning under uncertainty[J].Omega, 2007, 35(5): 563-577.

[4] Hartmann S.Projectschedulingunderlimitedresources:mo-dels,methods,andapplications[M].Berlin: Springer Science & Business Media, 2012.

[5] Ghomi S M T F, Ashjari B. A simulation model for multi-project resource allocation[J].InternationalJournalofProjectManagement, 2002, 20(2): 127-130.

[6] Wu M C, Sun S H. A project scheduling and staff assignment model considering learning effect[J].TheInternationalJournalofAdvancedManufacturingTechnology, 2006, 28(11/12): 1190-1195.

[7] Ahlemann F, El-Arbi F, Kaiser M G, et al. A process framework for theoretically grounded prescriptive research in the project management field[J].InternationalJournalofProjectManagement, 2013, 31(1): 43-56.

[8] Zhang S T, Lu X. An evaluation index system of resources allocation efficiency of construction program[J].JournalofEngineeringManagement, 2014, 28(4): 108-112. (张双甜, 陆鑫. 建设项目群资源配置效率评价指标研究[J].工程管理学报, 2014, 28(4): 108-112.)

[9] Nieto-Morote A, Ruz-Vila F. A fuzzy approach to construction project risk assessment[J].InternationalJournalofProjectManagement, 2011, 29(2): 220-231.

[10] Amiri M P. Project selection for oil-fields development by using the AHP and fuzzy TOPSIS methods[J].ExpertSystemswithApplications, 2010, 37(9): 6218-6224.

[11] Schniederjans M.Goalprogramming:methodologyandapplications[M].New York: Springer Science & Business Media, 2012.

[12] Xu X H, Cai C G, Liang D. Complex multi-stage decision making method based on mixed multi-attribute information[J].SystemsEngineeringandElectronics,2015, 37(10): 2315-2321. (徐选华, 蔡晨光, 梁栋. 基于混合多属性信息的复杂多阶段决策方法[J].系统工程与电子技术, 2015, 37(10): 2315-2321.)

[13] Büyüközkan G, Feyz1oglu O. A fuzzy-logic-based decision-making approach for new product development[J].InternationalJournalofProductionEconomics, 2004, 90(1): 27-45.

[14] Yatsalo B, Didenko V, Gritsyuk S, et al. Decerns: a framework for multi-criteria decision analysis[J].InternationalJournalofComputationalIntelligenceSystems, 2015, 8(3): 467-489.

[15] Lin S W. An investigation of the range sensitivity of attribute weight in the analytic hierarchy process[J].JournalofModelinginManagement, 2013, 8(1): 65-80.

Resource allocation model for technological innovation program

DAI Wei-xu1,2, WU Wei-wei1, YU Bo1, KONG Bao-hong1

(1. School of Management, Harbin Institute of Technology, Harbin 150001, China; 2. Institute ofSpacecraftSystemEngineering,ChinaAcademyofSpaceTechnology,Beijing100094,China)

Aiming at solving the problem of allocating resources of technological innovation program, the R&D employees are regarded as the key resource, and the procedures and assumptions of resource allocation of technological innovation program are proposed. Then the goals of time, cost and quality are set as constraints, and the multi-attributive utility functions of time, cost, and quality are created. Based on this, a resource allocation model for technological innovation program is constructed, which can achieve the comprehensive optimization of time, cost, and quality. Finally, a case is studied to demonstrate the effectiveness of the proposed model, which shows that the model is useful for making decision on the allocation of the resources of national defense technological innovation program.

technological innovation; program; resource allocation; scheduling model

2016-02-22；

2016-03-30；网络优先出版日期：2016-06-19。

国家自然科学基金(71272175, 71472055)；国家博士后基金特别资助项目(201104424)；黑龙江省哲学社会科学研究规划项目(14B105)资助课题

F 273.1

10.3969/j.issn.1001-506X.2016.10.17

戴维序(1972-),男,高级工程师,博士研究生,主要研究方向为系统工程管理、项目管理。

E-mail:15321323952@189.cn

吴伟伟(1978-),男,副教授,博士研究生导师,博士,主要研究方向为技术创新与管理。

E-mail:wuweiwei@hit.edu.cn

于渤(1960-),男,教授,博士研究生导师,博士,主要研究方向为产业技术经济分析、技术创新与管理。

E-mail:yub@hit.edu.cn