移动荷载作用下薄壁曲线箱梁剪力滞效应分析

卢海林，蔡恒，汤正

（武汉工程大学资源与土木工程学院，湖北武汉430074）

移动荷载作用下薄壁曲线箱梁剪力滞效应分析

卢海林，蔡恒，汤正

（武汉工程大学资源与土木工程学院，湖北武汉430074）

采用有限元法研究了移动荷载作用下曲线箱梁剪力滞效应及主要结构参数对剪力滞效应的影响。结合曲线箱梁设计参数合理取值范围，通过建立不同腹板宽度、不同曲率半径下的曲线箱梁空间板壳有限元模型，对简支曲线箱梁剪力滞效应进行参数化分析，得到了荷载运动到跨中截面时跨中顶板应力分布及内外侧剪力滞系数变化规律。根据分析结果，利用最小二乘法提出了计算曲线箱梁剪力滞系数经验公式。分析结果表明：在移动荷载作用下，动剪力滞系数峰值出现在顶板与腹板交界处，最大值接近1.6，剪力滞效应严重；腹板宽度和曲率半径对箱梁剪力滞效应的影响十分明显，二者相互影响；外侧结点剪力滞系数峰值大于内侧；腹板宽度的增大和曲率半径的减小使外侧结点剪力滞效应更加显著，在车辆荷载作用下箱梁外侧部分更易遭到破坏。经验公式的计算结果与有限元分析结果相对误差为3.27%，满足工程计算要求。

移动荷载；曲线箱梁；剪力滞效应；有限元；回归分析；经验公式

箱型薄壁梁因结构轻，抗弯、抗扭刚度大等优点在国内桥梁和城市立交建设中得到了广泛的应用［1］。在箱型梁中，由于剪切变形沿箱梁翼板宽度方向的非均匀分布而引起的剪力滞效应［2］是造成一些重大工程事故的主要原因。目前，国内外对静载作用下截面形式简单的薄壁箱梁剪力滞效应进行了大量研究，取得了一些成果，集中荷载和均布荷载是采用最多的2种静载方式。而曲线箱梁受曲率半径的影响，会产生强烈的弯扭耦合效应，使其在动荷载（行车荷载、地震）作用下的变形和内力计算趋于复杂化。近年来，许多学者对箱梁动剪力滞效应也做了相应的研究：文献［3］依据哈密顿原理，推导了钢-混凝土连续组合箱梁控制微分方程和自然边界条件，并提出了一种对连续组合箱梁自振特性进行分析的计算方法；文献［4］用变分原理推导了考虑剪力滞效应的箱梁强迫振动微分方程、边界条件，建立了方程解的差分格式；文献［5］建立了薄壁箱梁桥在任意荷载作用下，考虑剪力滞剪切变形的振动分析理论体系；文献［6］基于有限条法和网格自动生成技术，进行了曲线箱梁弹性自由振动分析；文献［7］通过长期的现场检测，研究了一曲线箱梁桥在行车荷载作用下的自振特性和振动模式。可以看出，这些研究仅局限于研究剪力滞剪切变形对箱梁自振特性的影响，而对于在移动荷载作用下曲线箱梁考虑剪力滞效应的动力响应问题，研究非常有限。基于此，本文采用有限单元法，建立了不同腹板宽度、不同曲率半径下的曲线箱梁板壳有限元模型，重点分析了2种参数对曲线箱梁剪力滞效应的影响，探讨跨中截面顶板应力分布和动剪力滞系数变化规律，并根据回归分析法提出计算剪力滞系数经验公式，为研究此类结构提供参考。

1　曲线箱梁剪力滞效应解析理论

目前，针对曲线箱梁在静载作用下的剪力滞效应理论分析方法主要有比拟杆法和能量变分法，比拟杆法一般适用于求解直线箱梁，而能量变分法求得的应力虽然在翼板自由端存在较大误差，但获得的最大应力与实际应力相近，能够满足精度要求。

1.1基本假定

1）忽略阻尼影响，翼板应力沿板宽方向按三次抛物线分布，即

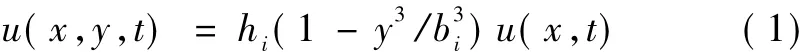
式中：u（x，y，t），u（x）分别为翼板纵向位移和剪力滞函数；h1（h2）为截面形心到上（下）翼板的距离；b1（b2）为翼板宽度的1/2（悬臂板的宽度）；t为厚度。

2）材料处于线弹性阶段，腹板符合平截面假定，而上、下翼板不符合。

曲梁在弯扭耦合作用下均匀纵向线应变ε0为

式中：w（x），θ（x）分别为箱梁竖向挠度和扭转角；r为箱梁曲率半径。

翼板由剪力滞翘曲位移产生的正应变ε1为

当腹板剪应变γ0=0时，翼板剪应变γ1为

曲线箱梁截面见图1。图中h为箱梁高度；tw为腹板厚度；t1，t2分别为上、下翼板的厚度；d为腹板宽度。

图1　曲线箱梁截面

1.2曲线箱梁应变能和荷载势能

翼板应变能Uf、腹板应变能Uw、自由扭转应变能Ut、翘曲扭转应变能Ur分别为

箱梁总的应变能U为

式中：qz为均布线荷载；mx为均布扭矩。

1.3剪力滞控制微分方程

考虑剪力滞效应后，在荷载作用下，产生了弯、扭、剪力滞的耦合，使得微分方程求解难度加大，文献［8］和［9］分别采用样条有限点法和传递矩阵法对微分方程进行了近似求解。本文介绍文献［10］中采用的伽辽金法。即假设曲线箱梁变形曲线按三角级数分布，即

式中，l为箱梁跨长。

将式（14）代入微分方程式（11）—（13），引入边界条件后可求出待定系数am，bn，ck（m，n，k=1，2，3，…），箱梁翼缘板正应力σi可表示为

2　曲线箱梁有限元模型

2.1结构形式

保持跨长1.308 m不变，分别建立4种不同腹板宽度d（200，300，400，500 mm）和曲率半径r（2.5，5.0，7.5，10.0，12.5 m）的20种箱梁模型。箱梁的材料和模型尺寸参考文献［11］，均为采用有机玻璃加工而成的曲线箱梁模型。材料弹性模量为3 000 MPa，泊松比为0.385，密度为1 180 kg/m。结构参数：t1=t2= 8 mm，tw=8 mm，h=100 mm。

2.2移动荷载加载形式

由于作用在结点的移动荷载是一种瞬间作用后随即消失的冲击荷载，因此在有限元建模中采用的是阶跃荷载形式［12］，使移动荷载由箱梁一端匀速移动至另一端，完成加载过程并进行数据采集分析。为了使模型上剪力滞效应更加明显，根据文献［13］，选择360 N的常量力在箱梁上移动来模拟行车荷载，速度为1 m/s，加载方式见图2。

图2　曲线箱梁结构加载方式（单位：cm）

3　动剪力滞效应计算结果分析

3.1移动荷载作用下箱梁顶板应力值

4个点同时以1 m/s的速度通过曲线箱梁，记录所用总时间为T，将加载时间调到T/2时，移动荷载重心刚好经过跨中截面L/2处，此时该截面上作用的效果最明显［14］。因此选择跨中截面为研究对象，取出该截面上结点号，读取应力后，绘制跨中位置处顶板截面应力曲线，见图3。可知：

1）在移动荷载作用下，曲线箱梁靠外侧结点所产生的应力值（绝对值，以下同）大于内侧，在顶板与腹板交界处形成峰值，并向两侧呈递减趋势，这与已有的静剪力滞研究结果一致，说明该现象在曲线箱梁中普遍存在，而与静、动荷载无关。

2）同一腹板宽度下，随着曲率半径的增加，顶板外侧同一结点应力逐渐减小，而内侧应力则逐渐增大。图3（d）中，当曲率半径为2.5 m时，外侧和内侧应力峰值之比达到1.56，剪力滞现象严重；当曲率半径为12.5 m时，二者峰值之比接近1.11，两侧应力分布大致对称，剪力滞影响程度有所减轻。

3）在相同曲率半径下，当腹板宽度由200 mm增加到500 mm的过程中，顶板内外侧同一结点应力值均减小；对于外侧结点，当曲率半径较小时，腹板宽度对结点应力影响较大，而对于内侧结点，当曲率半径较大时，腹板宽度对结点应力影响程度较大。

3.2腹板宽度和曲率半径对剪力滞系数的影响

箱梁翼板的应力集中现象在顶板与腹板交界处最明显，应力在此处达到峰值，剪力滞效应严重。

文献［2］中，定义剪力滞系数λ为

图3　不同腹板宽度、不同曲率半径时顶板截面应力曲线

式中：σ为箱梁实际的应力值；¯σ为按初等梁理论计算的应力值。

分别读取上述20种模型中荷载移动到曲线箱梁跨中位置时横截面顶板与腹板交界处实际产生的应力，考虑荷载加载形式为移动荷载，故¯σ可以等效为顶板应力分布曲线与翼板宽度所包围的面积除以翼板宽度。本文近似取有限元模型中各结点应力平均值，按式（16）计算得到顶板与腹板交界处内、外侧的剪力滞系数峰值，见表1。峰值曲线见图4。

3.3分析与讨论

由表1和图4可知：

1）曲线箱梁外侧结点剪力滞系数大于内侧，在半径为2.5 m时最大值为1.597，剪力滞效应严重；而内侧剪力滞系数仅在腹板宽度较小时才＜1，依次为0.941，0.945，0.955，表现出了负剪力滞现象。

2）腹板宽度增大时，梁肋相对刚度减小，翼板剪切变形增大，导致箱梁顶板内侧和外侧剪力滞系数均增大。以曲率半径2.5 m，5.0 m时外侧剪力滞系数为例，在腹板宽度为200 mm时，二者剪力滞系数之差为5.7%，300 mm时为13.9%，而在500 mm时达到了16.3%。说明箱梁腹板宽度越大，则曲率半径对剪力滞效应的影响越明显，腹板宽度和曲率半径这2个因素相互影响。对于外侧结点，越靠近表格右上方，剪力滞系数越大。

3）当曲率半径增加时顶板外侧剪力滞系数逐渐减小，而内侧剪力滞系数逐渐增大，腹板宽度为200 mm时，外侧剪力滞系数依次为1.237，1.180，1.138，1.102，1.101，减小幅度为5.7%，4.2%，3.7%，0.1%，内侧剪力滞系数为0.941，1.002，1.045，1.082，1.084，增大幅度为6.1%，4.3%，3.7%，0.2%，幅度均在减小。此外，内、外侧剪力滞系数曲线斜率（绝对值）不断减小，表明曲率半径增大时，箱梁剪力滞效应减弱。

表1　不同腹板宽度和曲率半径下顶板剪力滞系数峰值

图4　不同腹板宽度、不同曲率半径时顶板剪力滞系数峰值曲线

4　经验公式

剪力滞效应的另一种表示方式为有效分布宽度，国内外以翼板有效宽度的形式将剪力滞效应的影响写到规范中［15-16］，但利用有效宽度计算截面的最大应力常常偏小。因此，本文选用剪力滞系数作为曲线箱梁剪力滞效应计算公式。

根据有限元参数分析结果：宽径比越大，外侧结点剪力滞系数峰值也越大。通过前文研究表明腹板宽度和曲率半径对曲线箱梁剪力滞效应影响比较大。结合图3、图4曲线特点，对外侧结点剪力滞系数峰值按四次抛物线进行曲线拟合，即

式中：λmax为外侧结点剪力滞系数峰值；C1～C5为宽径比影响系数。

根据最小二乘法和参数分析的有限元模型计算结果进行回归分析，可以求得式（17）中各项系数分别为C1=0.8，C2=23.2，C3=-322.6，C4=1 904，C5= -3 846.6。将该结果与有限元分析结果进行比较，二者相对误差为3.27%，满足工程计算精度要求。

5　结论

1）在移动荷载作用下，单箱单室简支曲线箱梁跨中截面顶板外侧结点正应力大于初等梁理论的计算值，呈明显的正剪力滞现象；对于内侧结点，仅在曲率半径和腹板宽度较小时表现出了负剪力滞现象；曲线箱梁截面正应力主要集中在腹板与顶板交界附近一定区域，其它区域正应力分布相对较小。

2）曲线箱梁跨中截面顶板外侧剪力滞系数峰值相对大于内侧，即外侧剪力滞效应较内侧严重。当荷载沿中心线移动时，外侧部分更容易遭到破坏，应引起足够重视。

3）通过有限元法对曲线箱梁的参数敏感性进行分析，发现腹板宽度和曲率半径是影响箱梁翼板剪力滞效应的主要参数，且二者对剪力滞效应相互影响。对于外侧结点，曲率半径减小和腹板宽度增大对剪力滞呈叠加效应。根据这一影响，利用最小二乘法通过回归分析得到曲线箱梁剪力滞系数经验计算公式，且与有限元分析结果比较，误差较小，能满足工程精度要求。

4）曲率半径增大时，腹板宽度成为影响箱梁剪力滞效应的主要参数，影响程度随曲率半径的增大而减小。箱梁以受弯和受剪切为主。当曲率半径足够大时，可忽略扭转效应，按直线箱梁分析计算。

［1］郭金琼，房贞政，郑振.箱型梁设计理论［M］.北京：人民交通出版社，2008.

［2］张士铎，邓小华，王文州.箱型薄壁梁剪力滞效应［M］.北京：人民交通出版社，1998.

［3］ZHOU W B，JIANG L Z，YU Z W.Analysis of Free Vibration Characteristic of Steel-concrete Composite Box-girder Considering Shear Lag and Slip［J］.Journal of Central South University，2013，20（9）：2570-2577.

［4］刘建新，马麟，胡庆安.薄壁箱梁振动时的剪力滞效应［J］.郑州大学学报，2008，29（3）：122-128.

［5］康琦，马麟，徐岳.剪力滞后剪切变形对薄壁箱梁的振动影响［J］.江南大学学报，2009，8（1）：94-98.

［6］TAYSI N，OZAKC M.Free Vibration Analysis and Shape Optimization of Box-girder Bridges in Straight and Curved Planform［J］.Engineering Structures，2002（24）：625-637.

［7］HUGO C G，PAUL J F，MARIA Q F，et al.Testing and Long Term Monitoring of a Curved Concrete Box Girder Bridge［J］. Engineering Structures，2011，33（10）：2861-2869.

［8］段海娟，赵人达，周益云.曲箱梁考虑剪力滞效应的弯扭耦合分析［J］.中国铁道科学，2002，23（1）：36-39.

［9］何云勇.一种分析曲线箱梁剪力滞效应的传递矩阵法［J］.重庆交通大学学报，2010，29（5）：670-673.

［10］王岚，李长凤，邢永明.曲线箱梁剪力滞效应的弹性分析［J］.公路交通科技，2008，25（7）：65-69.

［11］卢海林.预应力混凝土曲线箱梁剪力滞效应理论分析与试验研究［D］.天津：天津大学，2005.

［12］王新敏.ANSYS工程结构数值分析［M］.北京：人民交通出版社，2007.

［13］卢海林，张伟，颜昌雄.移动荷载速度对悬臂曲线箱梁剪力滞效应的影响［J］.武汉工程大学学报，2014，36（3）：18-21.

［14］莫金利.车辆动荷载作用下预应力混凝土曲线箱梁桥剪力滞效应分析［D］.石家庄：石家庄铁道大学，2013.

［15］中华人民共和国交通部.JTG D62—2004公路钢筋混凝土及预应力混凝土桥涵设计规范［S］.北京：人民交通出版社，2004.

［16］Deutsches Institute for Normung.DIN 1075 Concrete Bridges：Dimensioning and Construction［S］.Geneva：International Organization for Standardization，1981.

Analysis on Shear Lag Effect of Thin-Walled Curved Box Girder Under Moving Load

LU Hailin，CAI Heng，TANG Zheng
（School of Resource and Civil Engineering，Wuhan Institute of Technology，Wuhan Hubei 430074，China）

Shear lag effect of curved box girder and the influence of main structure parameters on it under moving load were investigated by using the finite element method.Considering the reasonable ranges of design parameters of curved box girder，parametric analysis on shear lag effect of simply supported curved box girder was performed by setting spatial shell finite element models under different web widths and curvature radii，therefore the change rules of stress distribution in the roof of mid-span section and shear lag coefficient inside and outside were obtained when the loads moved to the mid-span.Based on the analysis，the empirical formula was proposed to calculate shear lag coefficient of curved box girder with the least square method.T he results show that under moving loads，the peak dynamic shear lag coefficients present at the junction of roof and web，the maximum of it nearly reaches 1.6，shear lag effect is severe.Shear lag effect is greatly influenced by web width and curvature radius which affect each other，peak shear lag coefficients of outer nodes are bigger than that of inner，for outer nodes，the increasing of web width and decreasing of curvature radius make shear lag effect more prominent.T he outer part of box girder is damaged more easier under vehicle loads.T he relative error between the results of proposed empirical formulas and finite element method is 3.27%，which meets the need of engineering calculation.

M oving load；Curved box girder；Shear lag effect；Finite element；Regression analysis；Empirical formula

U448.42

ADOI：10.3969/j.issn.1003-1995.2016.09.04

1003-1995（2016）09-0014-05

（责任审编郑冰）

2016-03-23；

2016-07-29

国家自然科学基金（51378404）；武汉工程大学创新基金（CX2015042）

卢海林（1965—），男，博士，教授。