基于EIGEN6C2模型的Kaula规则精化

梁建青，沈云中，张兴福

(1.同济大学 测绘与地理信息学院，上海 200092；2.广东工业大学 测绘工程系，广东 广州 510006)



基于EIGEN6C2模型的Kaula规则精化

梁建青1，沈云中1，张兴福2

(1.同济大学 测绘与地理信息学院，上海 200092；2.广东工业大学 测绘工程系，广东 广州 510006)

高精度重力场模型精化Kaula规则其要点是将Kaula规则乘上一个与位系数阶数项相关的二阶有理函数，并基于EIGEN6C2重力场模型解算有理函数模型的系数。精化后的Kaula规则与EIGEN6C2模型和EGM2008模型的逼近误差都只是原来Kaula规则的0.26%。因此, 精化后的Kaula规则更能正确表示各阶引力位的实际能量，对于重力场模型的解算提供更加合理的约束。

重力场模型；Kaula规则；EIGEN6C2模型；EGM2008模型；精化

1966年Kaula给出重力场信号的Kaula阶方差模型，即著名的Kaula规则，以非常简单的模型刻画地球重力位系数的能量。Kaula规则常用于构造正则化解[1]，当观测数据存在空白以及卫星重力反演的向下延拓等原因造成解算模型病态时，Kaula规则的约束对于合理求解重力场位系数有非常重要的作用[2]。目前，Kaula规则约束的正则化方法已经用于GOCE卫星数据的重力场反演[3-7]。例如，欧空局已经基于最小二乘法反演的第五代GOCE重力场模型中均采用Kaula规则约束。由于GOCE卫星的极区空白导致采用最小二乘法求解重力场位模型的法方程是病态的，重力场位系数低次项受极区空白的影响比较大，因此无法更好地求解重力场位系数。而Kaula规则的合理约束对利用GOCE卫星观测数据反演更高阶次的重力场模型具有重要意义。至今，已有许多学者研究Kaula规则构造的正则化解在GOCE卫星反演重力场中的作用[4,6-7]，或者利用Kaula规则分析几个现有的重力场模型[8]，但是对精化Kaula规则的研究却是比较少。

虽然Kaula规则用非常简单的模型给出了重力场位系数各阶能量分布的统计规律[1]，但是其与采用重力卫星观测数据和其它数据反演的许多目前高精度地球重力场模型的实际阶方差存在差异，尤其是高阶部分，因此本文基于高精度重力场模型研究Kaula规则的精化，使得精化后的Kaula规则能更加正确地反映引力位的实际能量分布,从而为重力场位系数的解算提供更加合理的约束。本文首先分析EIGEN6C2模型的阶方差与Kaula规则曲线之间的差异，然后将Kaula规则乘上一个与位系数阶数项相关的二阶有理函数，并基于EIGEN6C2重力场模型解算有理函数模型的系数。最后再利用GOCE卫星2011年1～2月的轨道和梯度数据反演重力场来验证精化Kaula规则的必要性。

1　EIGEN6C2模型阶方差分析

在地固坐标系中，地球引力位算式为

(1)

(2)

1966年Kaula给出重力场信号的理论公式[9]，即著名的Kaula规则，其阶方差算式为

(3)

根据式(2)、式(3)可得到直至1 949阶次的EIGEN6C2模型和Kaula规则的阶方差图(见图1)以及两者的差异(见图2)。

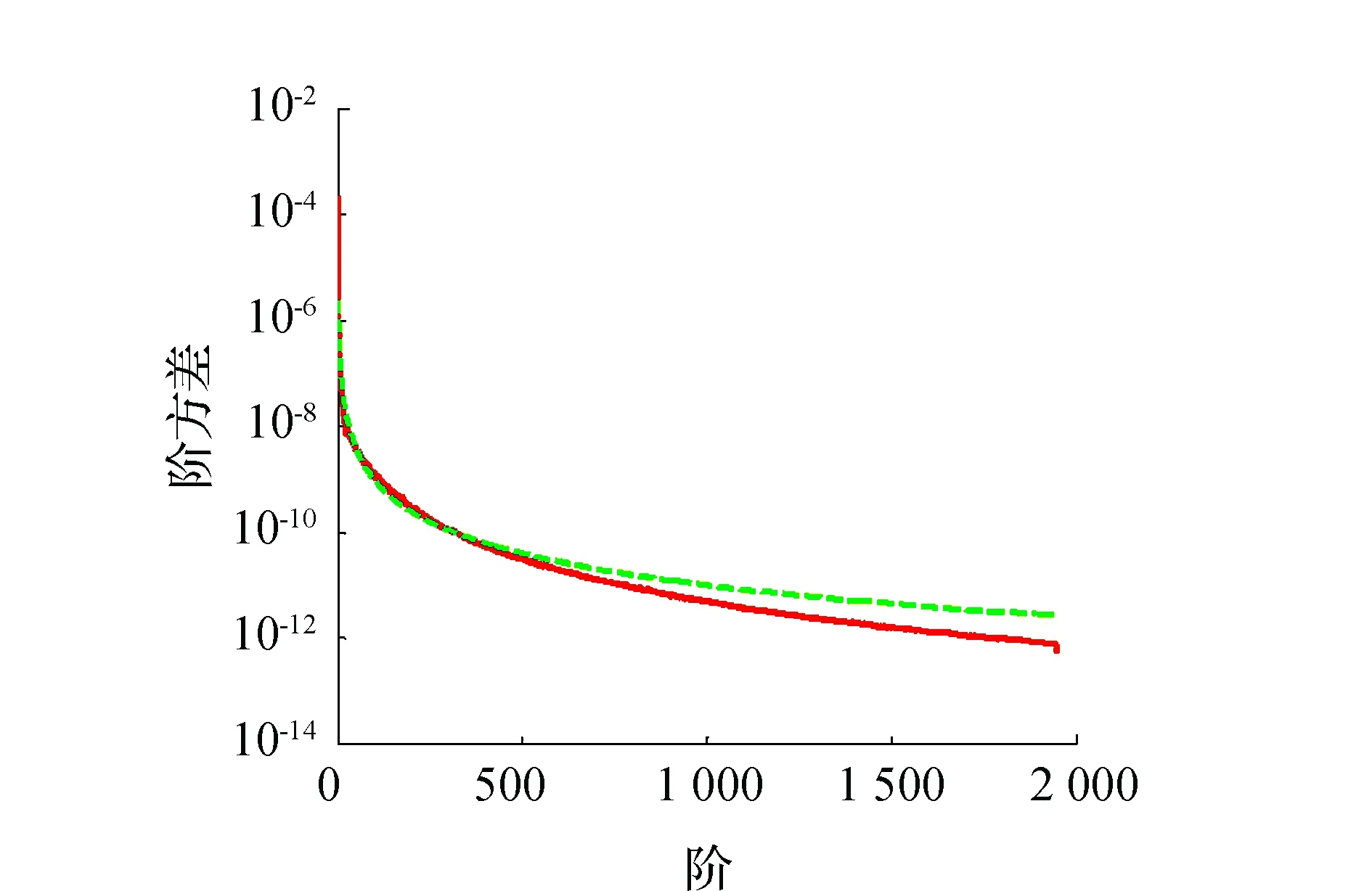
图1　EIGEN6C2模型阶方差(实线)和Kaula规则阶方差(虚线)

图2　EIGEN6C2模型与Kaula的阶方差之差

图1和图2表明， Kaula规则2阶系数的阶方差比EIGEN6C2模型小约两个数量级， 4～50阶稍微大于EIGEN6C2模型，50～300阶小于EIGEN6C2模型，300～1 949阶大于EIGEN6C2模型。随着模型阶次的增大, Kaula规则阶方差减小的速度小于EIGEN6C2模型，因此当n>300时，Kaula规则的阶方差与EIGEN6C2模型之间的差值不断增大。

2　基于EIGEN6C2模型的Kaula规则精化方法

图1和图2表明，EIGEN6C2模型的阶方差与Kaula规则之差和位系数的阶有关，如果精化后的Kaula规则的阶方差为

(4)

(5)

图3　参数与位系数阶的关系(n>2)

(6)

(7)

3　结果及分析

(8)

图4　拟合参数比较结果图(n>2)

Kaula规则与EIGEN6C2模型的符合程度可根据其逼近中误差来衡量，其算式为

(9)

图5　精化前、后的Kaula规则与EIGEN6C2模型阶方差

图6　精化前、后的Kaula规则与EGM2008模型的阶方差

为进一步验证本文对Kaula规则精化的合理性，以GOCE卫星2011年1～2月的轨道和梯度观测数据基于直接解法反演200阶次的地球重力场为例，分别采用精化前、后的Kaula规则构造正则化矩阵约束GOCE卫星反演的法方程，并基于恢复的大地水准面累积误差最小确定最优正则化参数。其中，参考模型为EIGEN5C，截断至200阶次，最后相对于EIGEN6C2模型评定解算结果的精度。精化前、后的Kaula规则约束后的重力场模型在200阶大地水准面累积差分别为9.36 cm，9.35 cm，表明本文反演结果是正确的。精化前、后的Kaula规则约束后的大地水准面误差如图7所示。

图7　精化前、后的Kaula规则约束后的大地水准面误差

由上述结果和图可见，因Kaula规则在200阶之前与EIGEN6C2、EGM2008模型符合较好，因此这部分改进空间非常小，所以精化后的Kaula规则约束的大地水准面误差并没有多大的变化(见图7)。但是本文精化后的Kaula规则与EIGEN6C2和EGM2008模型在高阶部分的吻合程度显著提高，其更能准确地反映引力位的实际能量分布(见图5，图6)。

4　结束语

本文根据高精度的重力场模型对Kaula规则进行精化，并根据EIGEN6C2模型解算精化模型的系数，精化模型的拟合优度达到0.9775，说明拟合度较佳。精化后的Kaula规则与EIGEN6C2模型和EGM2008模型的逼近误差只是精化前的0.26%，说明精化后的Kaula规则与EIGEN6C2和EGM2008模型符合较好。因此，本文精化后的Kaula规则更能正确反映出各阶引力位的实际能量，这在很大程度上精化原来的Kaula阶方差模型，为以后利用Kaula规则构造正则化矩阵解算更高阶次的GOCE重力场模型提供合理的依据。

[1]沈云中.应用CHAMP卫星星历精化地球重力场模型的研究[D].武汉：中国科学院测量与地球物理研究所,2000.

[2]王正涛.卫星跟踪测量确定地球重力场的理论和方法[D].武汉：武汉大学，2005.

[3]徐新禹，李建成,王正涛,等.Tikhonov正则化方法在GOCE重力场求解中的模拟研究[J].测绘学报,2010,39(5):466-470.

[4]郑伟，许厚泽,钟敏.基于时空域混合法利用Kaula正则化精确和快速解算GOCE重力场[J].地球物理学报,2011,54(1):14-21.

[5]METZLER B,PAIL R.GOCE Data Processing: the Spherical Cap Regularization Approach [J].Stu.Geophy.Geod,2005,49(4):441-462.

[6]KUSCHE J,KLEES R.Regularization of gravity field estimation from satellite gravity gradients[J].Journal of Geodesy,2002,76(6):359-368.

[7]YI W.The Earth’s gravity field from GOCE[D].Germany:Technische Universitat Munchen,2011.

[8]周星，甄冬松.利用Kaula准则分析几种地球重力场模型[J].城市建设理论研究，2012(34).

[9]KAULA W.Theory of satellite geodesy[M].Waltham,Mass.Blaisdell Pub.Co.,1966.

[10] 沈云中，陶本藻.实用测量数据处理方法[M].2版.北京: 测绘出版社，2012.

[11] 唐家德.基于MATLAB的非线性拟合[J].计算机与现代化,2008(6):15-19.

[责任编辑：张德福]

A modified Kaula rule based on EIGEN6C2 gravity field model

LIANG Jianqing1, SHEN Yunzhong1, Zhang Xingfu2

(1.School of Surveying and Geo-informatics, Tongji University, Shanghai 200092，China；2. Department of Surveying and Mapping，Guangdong University of Technology,Guangzhou 510006，China)

The paper will modify the Kaula rule based on the EIGEN6C2 gravity field model. The key point is to multiply a degree related second order rational function to the Kaula rule. The coefficient parameters of the rational function are estimated based on the EIGEN6C2 gravity field model. The approximation error of the modified Kaula rule with respect to EIGEN6C2 and EGM2008 gravity field models are only 0.26% of that of the original Kaula rule. Therefore the modified Kaula rule can more reasonably reflect the power spectrum of the earth’s gravity field, which can be used as a constraint in computing the gravity field model.

gravity field model; Kaula rule; EIGEN6C2 model; EGM2008 model; modifying

10.19349/j.cnki.issn1006-7949.2016.12.005

2015-06-22

国家自然科学基金资助项目(41474017； 41274035)

梁建青(1990-)，男，硕士研究生.

P223

A

1006-7949(2016)12-0021-04