扩展无网格法分析功能梯度材料断裂问题

张保文， 马文涛， 黄凌霄

（宁夏大学数学计算机学院，宁夏银川 750021）

扩展无网格法分析功能梯度材料断裂问题

张保文， 马文涛， 黄凌霄

（宁夏大学数学计算机学院，宁夏银川 750021）

提出一种扩展无网格法模拟二维功能梯度材料I、II型复合断裂问题.基于单位分解思想，在EFGM近似函数中分别添加阶跃函数和奇异函数，依次表征不连续位移场和裂尖奇异应力场.结合一种不需要求解梯度材料参数的互作用积分的域形式计算了复合型应力强度因子.两个功能梯度板的数值算例验证了单位分解扩展无网格法的可行性和有效性.

功能梯度材料；EFGM；扩展无网格法；应力强度因子

非均匀性是导致材料力学性质复杂的主要原因之一.功能梯度材料（FGMs）是一类十分特殊的非均匀材料，其组成、结构和物理力学性质在空间上主要沿某一方向变化而在垂直于这个方向的平面或曲面上的变化往往非常小.天然材料中的生物材料和岩土材料往往具有FGMs的性质.近年来，FGMs在机械、生物、化学、电子等工程领域中也得到了广泛的应用，其力学性质成为研究的热点.由于材料结构和组成不同，不同梯度材料的细观、宏观断裂机理也不同.在细观、宏观尺度上，裂纹和孔洞对梯度材料结构的力学性质有着重要的影响.对这些缺陷进行力学分析成为梯度材料研究的一个分支，也成为断裂力学研究的热点［1］.

FGMs的早期研究可追溯到1960年，Gibsin将土视为非均匀材料［2］.由于问题的难度和复杂程度都很高，含裂纹的FGMs往往被假定为弹性模量是关于空间坐标变化的线性函数或指数函数.Erdogan等［3］和Eischen等［4］分别采用理论分析和有限单元法证明了FGMs和各向同性材料的裂尖应力场都具有的奇异性.Kim和Paulino［5］采用三种不同的方法：路径无关J积分方法、修正的裂纹闭合积分法和位移修正方法计算了FGMs的应力强度因子.Dolbow和Gosz［6］在FGM断裂分析中引入相互作用积分计算了二维复合应力强度因子.他们的研究表明，与传统的J积分相比，相互作用积分显得更为方便，因为后者无需计算沿自由裂纹面的应变能密度.Kim和Paulio［7］采用FEM和相互作用积分计算了各向同性FGM上的复合应力强度因子.Rao和Raham［8］采用相互作用积分和无网格法求解了FGMs的应力强度因子.Kim和Paulio［9］还总结了三种不同辅助场的定义，讨论了如何获取复合型应力强度因子和T应力的方法.Yu等［10］提出了一种无需计算材料梯度的相互作用积分，并结合扩展有限元计算了非各向同性材料的I、II复合应力强度因子.Mojdehi等［11］采用无网格局部－Petrov－Galerkin（MLPG）分析了三维静态和动态功能梯度厚板问题，但未涉及板内包含裂纹的情况.Zhang和Kim［12］推导了二维各向异性FGM的裂尖奇异应力场，指出高阶项受材料梯度的影响非常大，在奇异裂尖场中扮演着重要的角色.

近年来，无网格法被广泛应用于求解断裂力学问题.由于无网格法只需节点信息，而不需要单元之间的连接信息，因此很容易避免传统FEM方法中面临的网格划分和重构带来的巨大困难.目前，无网格法的研究主要集中于均匀材料的断裂分析，极少有人关注和将其应用于FGMs中［13］.基于此，本文主要的工作是利用单位分解扩展无网格法求解FGMs的复合应力强度因子.该方法与传统的内部基扩展无网格法不同，无需使用修改权函数的方法，裂纹的几何位置由符号距离函数表达，裂纹所引起的不连续性和裂尖奇异性则由近似函数中的不连续项和裂尖奇异项表达.由不需要计算材料参数导数的相互作用积分的域形式，计算了不

同梯度材料的复合应力强度因子.

1　单位分解扩展无网格法

1.1移动最小二乘近似（MLS）

考虑区域中的函数，根据移动最小二乘（MLS）法，其近似函数可表示为

其中n节点x 影响域内包含的节点数目；ΦT（x）＝PT（x）A－1（x）C（x）；PT（x）＝｛1，x1，x2｝，A（x）＝PTWPT，C（x）＝PT（x）W；W（x）＝diag［W1（x），W2（x），…，Wn（x）］为与节点相关的权函数，本文选取为四次样条权函数；dT＝｛d1，d2，…，dn｝，dI为与节点I相关的参数.

1.2不连续近似函数

传统的MLS只能构造连续的近似函数，针对含裂纹的不连续问题，必须对其进行改进.本文采用单位分解法对MLS进行修改，得到不连续位移场函数.其基本思想是在MLS近似函数中添加阶跃函数项和裂尖奇异项，分别表征由裂纹导致的不连续位移场和裂尖奇异应力场.该方法的思想类似XFEM，其近似函数在裂纹周围一狭小区域内（大小由节点影响域半径确定）是不连续的，在远离裂纹的区域内则是光滑连续的.单位分解扩展无网格法已被成功应用于模拟黏聚裂纹［13］、裂纹开裂［14］和岩体材料接触摩擦分析［15］等问题，本文将其应用于求解功能梯度材料断裂问题.

单位分解扩展无网格法近似函数可表示为

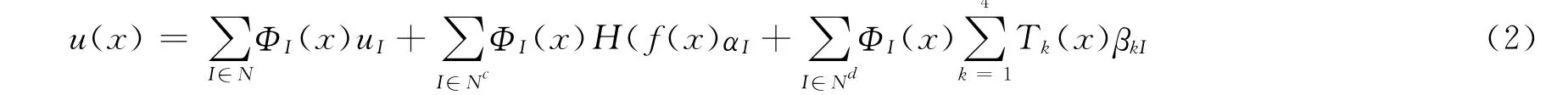
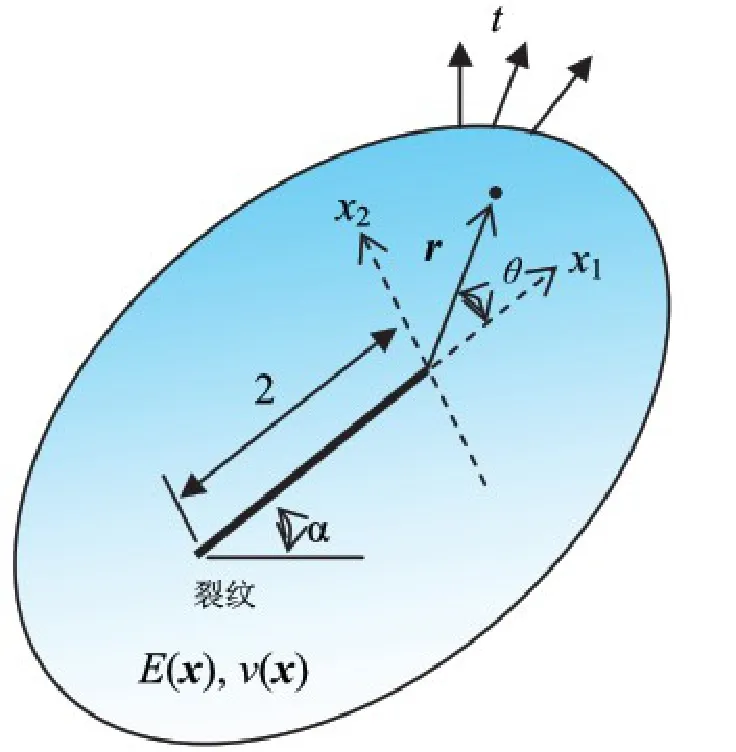
图1　含裂纹的功能梯度材料Fig.1 A crack in a functionally graded material

其中：N为整个计算区域内的节点集；Nc为节点影响域被裂纹完全切割的节点集；Nt为节点影响域部分被裂纹切割的节点集（见图1）.公式（6）中ΦI（x）为MLS形函数，第一项为标准的MLS近似函数；第二项为阶跃扩展函数，第三项为裂尖扩展函数.αI，βkI为引入的附加变量；通常，阶跃函数H（fI（x））取为符号距离函数，定义为

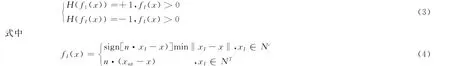
其中xup为裂纹尖端坐标，n为裂纹面法向.

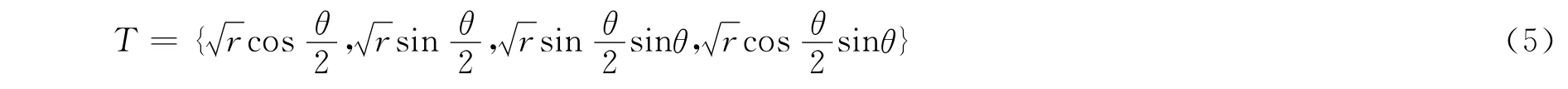
其中r，θ为以裂纹尖端为坐标原点的极坐标系（见图1）.

1.3弹性力学方程的弱形式及其离散化

二维弹性力学问题的虚功方程为

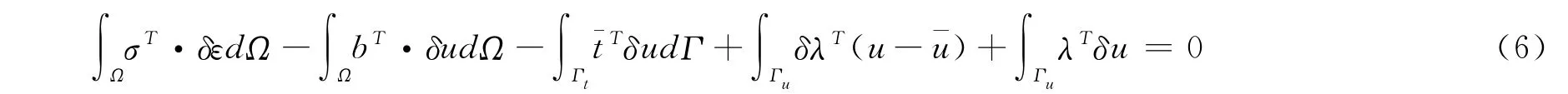
式中Ω为计算域，Γ＝Γu∪Γt为域边界，δε为虚应变向量，u＝［u v］T为位移向量，σ为与u对应的应力向量，b为体力向量，珋t为应力边界Γt给定的面力，珔u为位移边界Γu上给定的位移，λ为拉格朗日乘子向量.

将式（2）的不连续近似函数代入式（6）并考虑位移变分的任意性，可得节点的离散线性方程

其中Bstd由标准的MLS近似得到；Benr由扩展部分形成；当xI∈ΩΓ，则ΨI（x）是阶跃函数H（fI（x））；当xI∈ΩΛ，则ΨI（x）是扩展基函数Tα（x）.方程中的形函数N为1阶拉格朗日插值函数.D（x）为弹性矩阵，对于平面应力问题，

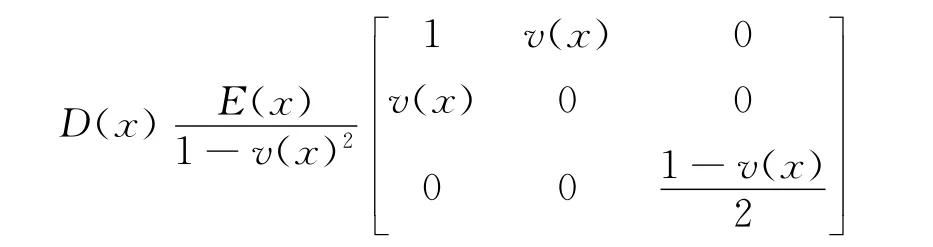
对于平面应变问题，

其中E（x）和v（x）分别为弹性模量和泊松比.对于各向同性材料，E（x）和v（x）均为常数；对于梯度材料，E（x）和v（x）则是随空间坐标变化的函数.

2　互作用积分

目前，在求解复合模式荷载作用下的应力强度因子时，互作用积分的域形式被广泛采用，也被证明是十分准确的方法.

2.1辅助场

在计算互作用积分时，辅助场起着至关重要的作用.通常有几种不同的形式，本文采用不完备形式.在裂尖局部极坐标下，其不完备形式定义为

其中KauxI和KauxII分别为I型和II型辅助应力强度因子，为一致张量.对应的函数和为

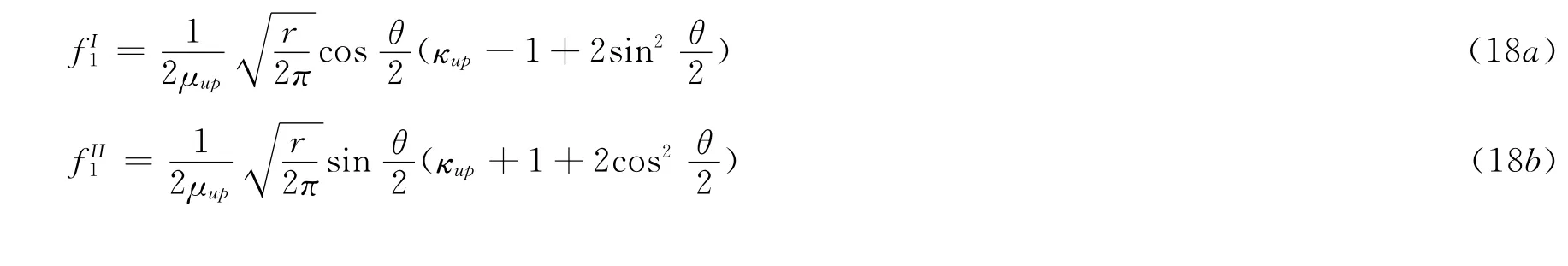
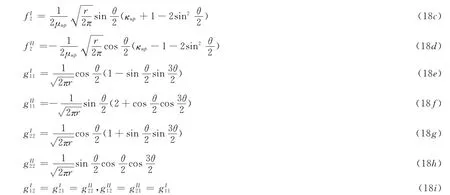
这里，κup＝3－4υup（平面应变）或κup＝（3－υup）／（1＋υup（平面应力），μup，υup分别为裂尖附近的剪切模量和泊松比.

2.2互作用积分的域形式

I型与II型复合应力强度因子可以通过互作用积分的区域形式（等效区域积分）计算.等效区域积分的具体形式为：

方程（19）中的第一项与均匀材料的公式是相同的.其中Supijkl为裂尖处的一致张量；A为由边界Γ＝Γ0＋Γ＋－Γs＋Γ－围成的积分区域（见图2）；q为足够光滑的权函数，要求在内边界Γs上为1，在外边界Γ0上为0.

在Dolbow等［6］、Kim等［7］、Rao等［8］的论文中，等效区域积分的形式中涉及到了材料参数的导数（Dijkl，1或Sijkl，1），公式（19）并不涉及材料参数的导数.在实际问题中，材料参数的导数很难确定，甚至根本不存在.因此公式比传统的等效区域积分更适合梯度材料的断裂分析，相应地，应力强度因子与互作用积分之间的关系为

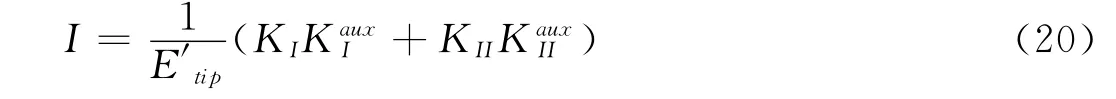
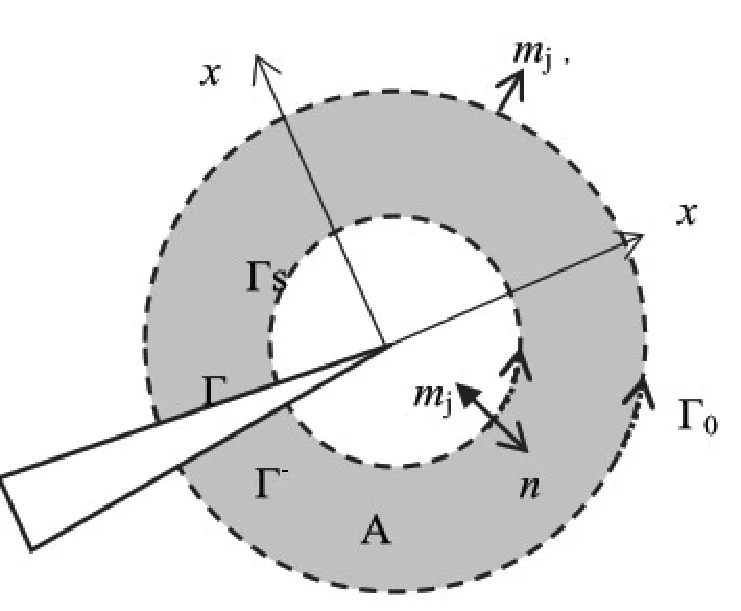
图2　互作用积分的积分区域Fig.2 Integral domain of interaction integral

其中E′tip＝Etip（平面应力）或E′tip＝Etip／（1－υtip）（平面应变）.Etip，υtip分别为裂纹尖端处的杨氏模量和泊松比.当KauxI＝1，KauxII＝0时，KI＝E′tipI／2，而当KauxI＝0，KauxII时，KII＝EtipI／2.

2.3互作用积分的无网格离散形式

为了在扩展无网格法中求解互作用积分，需要将方程离散为

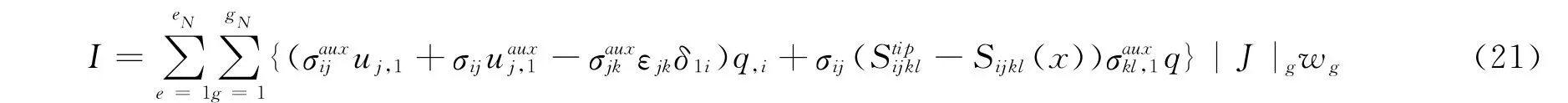
其中eN为积分区域A内的积分网格数目，gN为每个网格中的高斯积分点数.对于梯度材料，在建立刚度矩阵时采用积分点上的材料属性.

3　数值算例

采用MATLAB编写了扩展无网格法的相应程序.近似函数建立过程中采用四次样条权函数.圆形影响域半径取为1.7倍节点间距.公式（7）和（22）均采用背景积分网格计算.没有被裂纹切割的背景网格，采用16个高斯积分点；被裂纹切割的背景网格，将其分解为几个三角形网格，每个网格中采用36个高斯积分点.

3.1单边倾斜裂纹

考虑含有一条单边倾斜裂纹的二维平板问题，如图3所示.平板的长L＝2，宽W＝1.边裂纹倾角γ＝

E（x1）＝E珚exp［η（x1－0.5）］，0≤x1≤W

（22）

其中珚E和η是两个材料参数.在计算过程中，布置21 ×41个节点，20×40背景积分网格；珚E＝1和η依次取0，0.1，0.25，0.5和1.泊松比υ＝0.3.平板上部边界施加荷载σ22＝珋ε珚Eexp［η（x1－0.5）］（珋ε＝1），底部施加位移边界条件.表1比较了本文方法与Kim等［5］采用有限元法计算不同值对应的正则化应力强度因子及其相对误差.可以看出，本文方法与FEM的计算结果吻合得非常好.

3.2中心倾斜裂纹

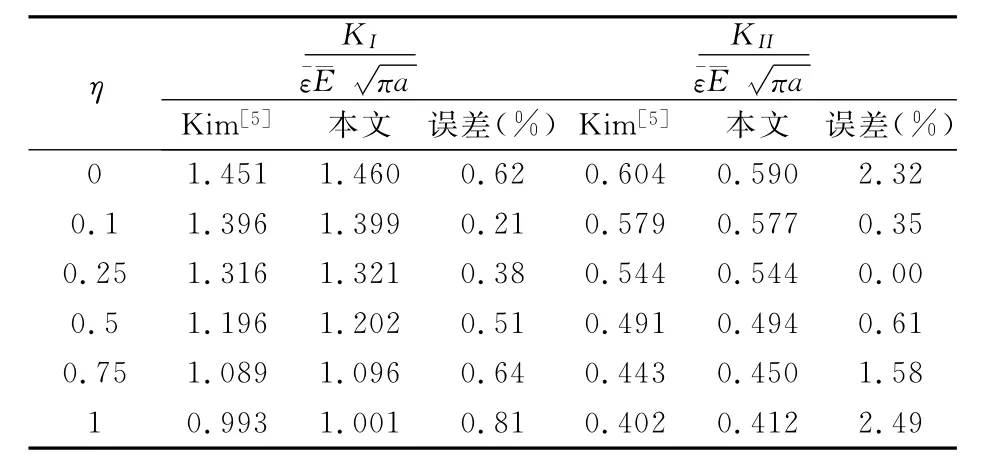
表1　倾斜裂纹的正则化应力强度因子Table 1 Normalized SIFs for a slanted crack in a plate

如图4所示，平板尺寸为2L＝2W＝20，中心裂纹长2a＝2，裂纹倾角为γ.计算过程中，泊松比υ＝0.3，弹性模量取为指数函数，具体形式为

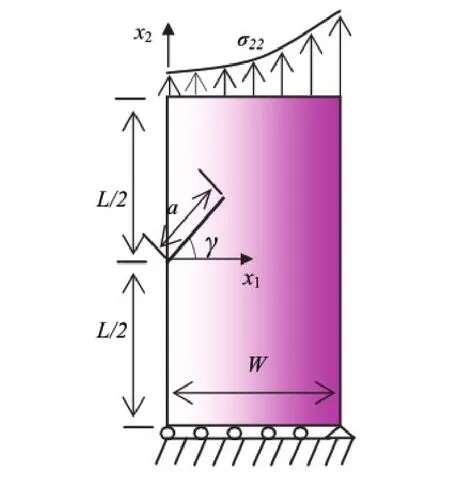
图3　复合荷载作用下的单边倾斜裂纹板Fig.3 Slanted crack in plate under mixed－mode loading

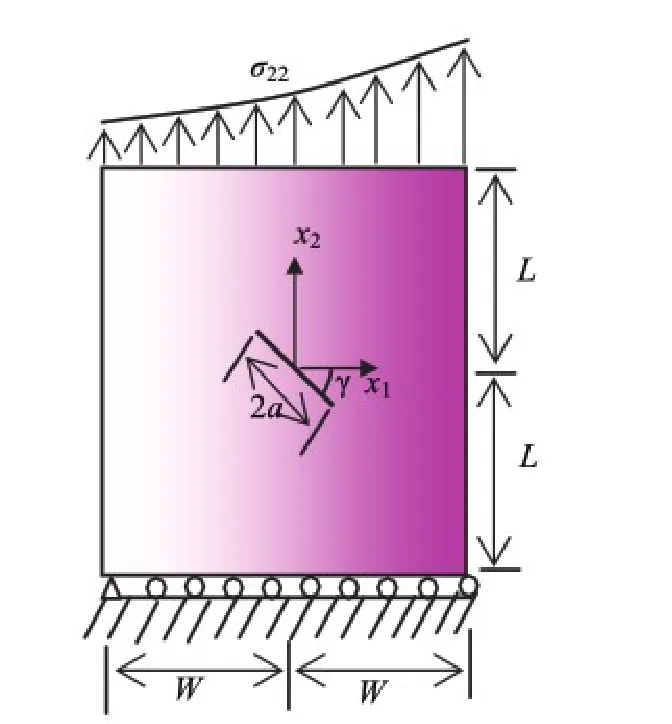
图4　复合荷载作用下的中心倾斜裂纹板Fig.4 Central inclined rack in plate under mixed－mode loading

其中材料参数珚E＝1，η依次取0.25和0.5.在平板顶部施加荷载σ22＝珋ε珚Eexp（ηx1）（珋ε＝1）.布置21×41个节点，20×40背景积分网格；γ／π依次取为0，0.1，0.2，0.3，0.4和0.5.Konda等［16］将该问题视为无限大平板问题得到相应的解析解.无网格法不能直接求解无限大区域问题，但当取a／W＝a／L≤0.01时，近似结果是可以接受的.表2和表3分别比较了当η＝0.25和η＝0.5时两个裂尖在不同γ／π值下对应的正则化应力强度因子的解析解和数值解.显然，本文方法与解析解十分接近.

表2　中心裂纹正则化应力强度因子（η＝0.25）Table 2 Normalized SIFs for a plate with an interior inclined crack（η＝0.25）

4　结论

本文提出单位分解扩展无网格法求解了二维功能梯度材料断裂力学问题.为了准确描述功能梯度材料裂纹的不连续位移场和裂尖奇异应力场，根据单位分解思想，在EFGM近似函数中添加了阶跃函数项和裂尖奇异函数项.采用一种修正的互作用积分域形式计算I型、II型复合应力强度因子.复合荷载作用下的边界斜裂纹算例和中心斜裂纹算例，研究了本文方法的有效性和计算精度.计算结果表明，本文方法非常适合求解功能梯度材料断裂问题，具有广阔的发展空间.

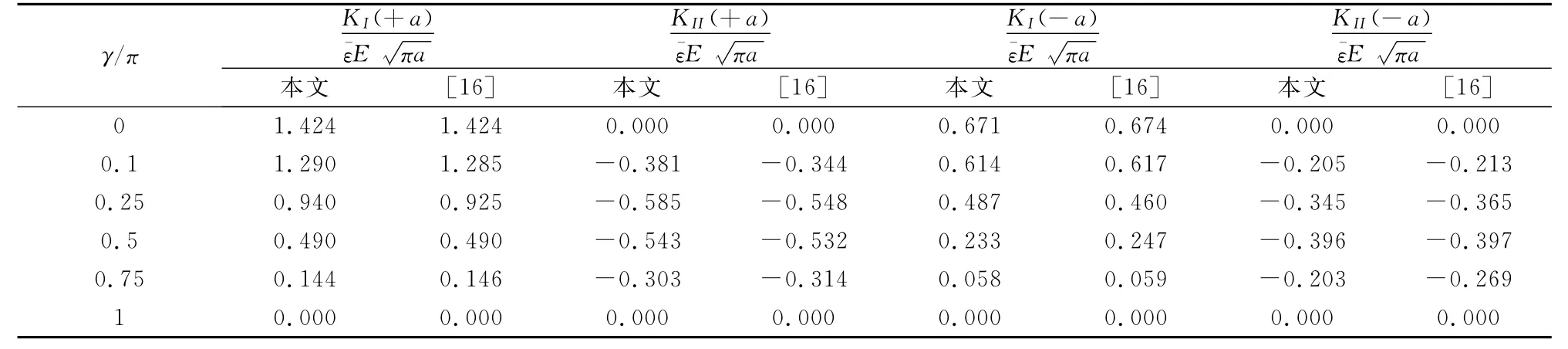
表3　中心裂纹正则化应力强度因子（η＝0.5）Table 3 Normalized SIFs for a plate with an interior inclined crack（η＝0.5）

［1］ XIZO H T，YUE Z.New Boundary element analysis of fracture mechanics in functionally graded materials［M］.Beijing：Higher Education Press，2011：25.

［2］ GIBSON R E.Some results concerning displacements and stresses in a non－homogenous elastic layer［J］.Geotechnique，1967，（17）：58－67.

［3］ DELALE F，ERDOGAN F.The crack problem for a nonhomogeneous plane［J］.International Journal of Applied Mechanics，1983，（50）：609－613.

［4］ EISCHEN J W.Fracture of nonhomogeneous materials［J］.International Journal of Fracture，1987，（34）：3－22.

［5］ KIM J H，PAULINO G H.Finite element evaluation of mixed mode stress intensity factors in functionally graded materials［J］.International Journal of Numerical Method in Engineering，2002，53（8）：1903－1938.

［6］ DOLBOW J E，GOSZ M.On the computation of mixed stress intensity factors in functionally graded materials［J］.International Journal of solids and structure，2002，39（9）：2557－2631.

［7］ KIM J H，PAULINO G H.An accurate scheme for mixed－mode fracture analysis of functionally graded materials using the interaction integral and micromechanics models［J］.International Journal of Numerical Method in Engineering，2003，（58）：1457－1479.

［8］ RAO B N，RAHMAN S.Mesh－free analysis of cracks in isotropic functionally graded materials［J］.Engineering Fracture Mechanics，2003，（5）：1－27.

［9］ KIM J H，PAULINO G H.T－stress，mixe－mode stress intensity factors，and crack initiation angles in functionally graded materials：a unified approach using the interaction integral method［J］.Computer methods in applied mechanics and engineering，2003，（192）：1463－1494.

［10］ YU H J，WU L Z，LI C G.Investigation of mixed－mode stress intensity factors for nonhomogeneous materials using an interaction integral method［J］.International journal of solids and structures，2009，（46）：3710－3724.

［11］ MOJDEHI A R，DARVIZEH A，BASTI A.Three dimensional static and dynamic analysis of thick functionally graded plates by the meshless local Petrov－Galerkin（MLPG）method［J］.Engineering analysis with boundary elements，2011，（35）：1168－1180.

［12］ ZHANG L H，KIM J H.Mixed－mode cracked－tip fields in an anisotropic functionally graded material［J］.Journal of applied mechanics，2012，（79）：1－10.

［13］ RABCZUK T，ZI G.A meshfree based on the local partition of unity for cohesive cracks［J］.Computational Mechanics，2006，39（6）：743－760.

［14］ 马文涛，师俊平，李宁.水平集与无网格耦合法在裂纹扩展中应用［J］.岩土力学，2012，33（11）：3447－3453.

［15］ 马文涛，师俊平，李宁.模拟摩擦接触问题的新型无网格数值方法［J］.岩土力学，2012，33（10）：3145－3150.

［16］ KONDA N，ERDOGAN F.The mixed mode crack problem in a nonhomogeneous elastic［J］.Engineering Fracture Mechanics，1994，47 （4）：533－545.

Enriched Meshless Analysis of Cracks in Functionally Graded Materials

ZHANG Bao－wen， MA Wen－tao， HUANG Ling－xiao
（School of Mathematics and Computer Science，Ningxia University，Yinchuan 750021，China）

An enriched meshless method was presented for analysing the mixed mode I and mode II fracture problem in two－dimension functionally graded materials.Both enriched functions，including jump function and crack tip singularity function，were added in the approximation of EFGM based on partition of unity.The mixed mode stress intensity factors for cracks in functionally graded materials were numerically evaluated using the modified domain form of interaction integral.The integrand does not involve any derivatives of materials properties.The numerical results were obtained for edge and center cracks，and were found to be in good with the reference solutions for the functionally graded material crack problems.

functionally graded materials；EFGM；enriched meshless method；stress intensity factors

TB301

A

1001－2443（2016）03－0230－06

10.14182／J.cnki.1001－2443.2016.03.005

2015－08－13

国家自然科学基金（51269024、41204041）.

张保文（1975－），男，硕士，讲师，复分析及其在力学中的应用.

引用格式：张保文，马文涛，黄凌霄.扩展无网格法分析功能梯度材料断裂问题［J］.安徽师范大学学报：自然科学版，2016，39（3）：230－236.