基于FPGA的图像多尺度特征点提取及匹配
2016-10-17刘桂华陈林宇肖得胜
刘桂华,陈林宇,肖得胜
(西南科技大学 信息工程学院,四川 绵阳 621000)
基于FPGA的图像多尺度特征点提取及匹配
刘桂华,陈林宇,肖得胜
(西南科技大学 信息工程学院,四川 绵阳 621000)
对于图像的多尺度特征点提取及匹配存在提取特征有限、算法复杂度高、处理速度慢的问题,提出了一种利用多尺度Harris角点方法提取图像中物体边界特征点,采用二维高斯拉普拉斯算子检测图像斑点信号,并基于SIFT特征描绘子计算特征描绘子相似度来完成匹配的方法。该方法充分利用FPGA的并行性特点,通过降低多尺度Harris角点检测、斑点提取和SIFT特征描绘子生成算法的复杂度,在FPGA中实现了图像多尺度特征点的快速提取及匹配。通过对多组图片进行对比测试验证,该方法相对于软件实现方法具有处理速度快,而图像主要特征点不丢失的特点。
FPGA;多尺度;Harris角点;梯度;SIFT
图像的多尺度特征点提取及匹配已经广泛运用于目标识别与跟踪、图像制导和影像处理等众多领域,是目标识别技术的核心研究内容之一[1]。角点作为图像的一种基本特征,具有不易受噪声影响、稳定性好、角点附近信息量大等优点,像Moravec,Harris和SUSAN等算法都是基于角点特征的算法[2]。Mikolajczyk和Schmid针对Harris角点算子不具有尺度不变性的缺点,在传统Harris角点检测算子中引入尺度空间理论,提出了Harris-Laplacian检测算子,从而使Harris检测算子具有尺度不变性[3]。David经过多年研究,于2004年提出SIFT[4](Scale-Invariant Feature Transform)算法,即尺度不变特征变换,在多个尺度下提取的特征点,包含了图像细节和轮廓信息,能实现更精确的匹配。
目前图像的多尺度特征点提取及匹配主要是通过计算机软件编程来实现,存在提取特征有限、算法复杂度高、处理速度慢等问题。对于实际应用中高分辨率图片的处理,CPU已经无法满足实时性的要求,目前主流趋势是利用CPU-GPU协同加速来完成[5-6]。相对于GPU而言,FPGA可脱离计算机独立运行,更适用于运动设备如移动机器人对图片的实时化处理。为了充分提取图像特征,提高特征提取和匹配的速度,本文基于FPGA(Field Programmable Gate Array)来实现图像多尺度特征点提取及匹配。采用多尺度Harris角点提取局部区域内图像亮度在多个方向发生变化的点;采用图像斑点提取与周围区域有着灰度变化的区域中心,并改进了SIFT特征描绘子的生成算法,使其具有可区分性并更利于FPGA的实现。不同尺度的特征点选择不同邻域的图像像素值进行描述,充分利用多尺度特征点的尺度信息,完成多尺度特征点的匹配。
1 系统结构
基于FPGA的图像多尺度特征点提取与匹配的整体系统框图如图1所示。首先FPGA对存储在SDRAM中的两幅图像进行图像多尺度表示,然后并行地对图像进行多尺度Harris角点提取和图像斑点提取,将提取到的两种特征点坐标合并作为多尺度特征点,并存储两类特征点数据。图像多尺度特征点匹配时,根据两幅图像的多尺度特征点坐标,通过SDRAM控制器分别从SDRAM中读出两幅图像多尺度特征点坐标邻域图像的灰度值,生成基于梯度的16维特征描绘子并存储在RAM中,最后对两幅图像特征点的特征描绘子进行相似度统计计算,使多尺度特征点之间具有区分性,完成多尺度特征点的匹配。
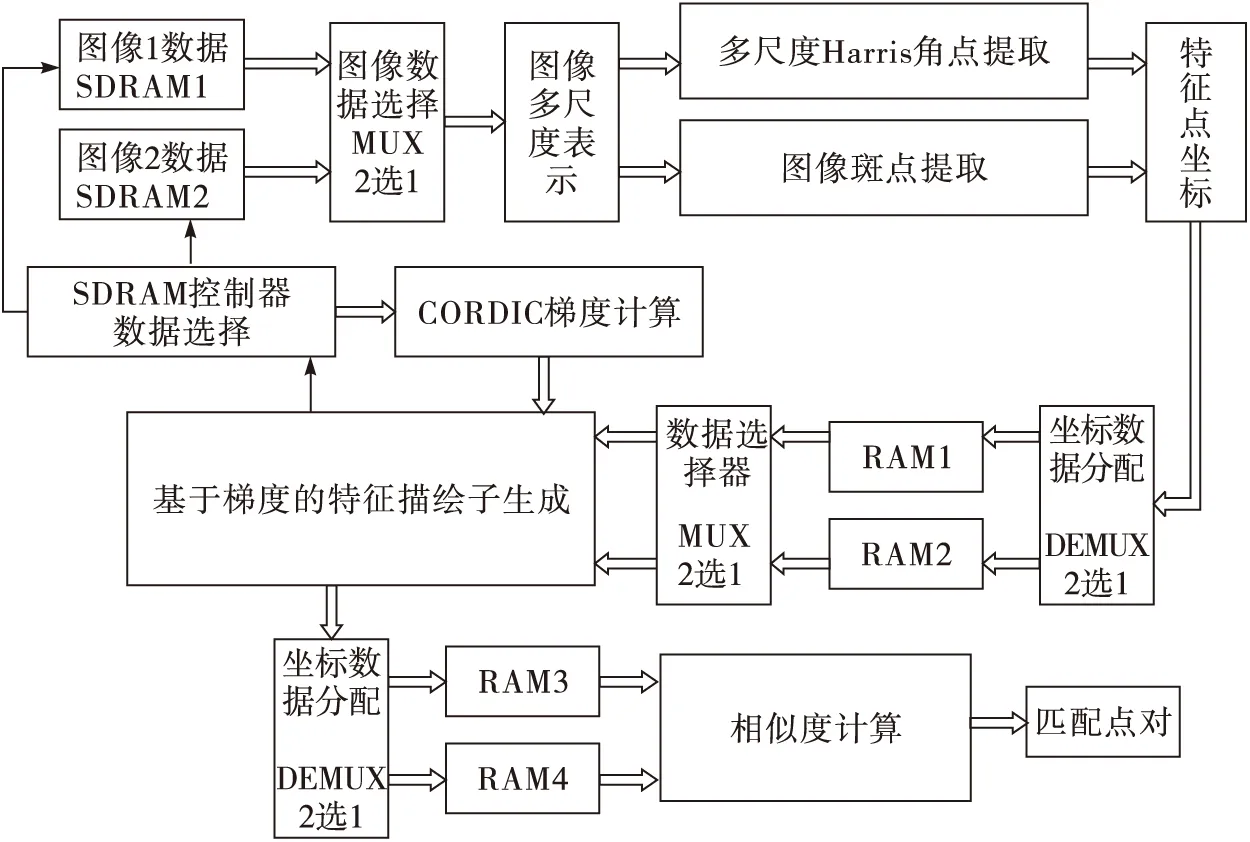
图1 多尺度特征点提取与匹配的整体系统结构
2 图像多尺度特征点提取的FPGA实现
本文采用多尺度Harris角点提取图像中物体边界的特征点,提出了利用二维高斯函数的拉普拉斯算子可以检测二维图像斑点信号。这两类特征点抗噪声能力较强,比较稳定,且其所在的区域含具有丰富的可利用信息。由于两种方法提取的特征点种类不一样,因此特征点坐标基本不重合。将两种方法结合,不仅增加了多尺度特征点的数量,更能充分提取图像的特征。针对FPGA的并行性结构特点,对多尺度Harris角点检测算法[7-8]、斑点提取算法进行改进,使得更利于FPGA的实现。
2.1多尺度Harris角点提取
Harris角点提取具有算法计算简单、检测效果好的特点,多尺度Harris角点提取算子将图像高斯尺度空间理论引入到Harris角点提取,使角点具有尺度不变性[3]。Harris角点提取主要包含高斯尺度空间的构建、位置及尺度空间响应值计算、多尺度Harris角点搜索3个主要步骤。
将二维高斯函数G(x,y,σ)与图像函数I(x,y)进行卷积,得到高斯尺度图像
L(x,y,σ)=G(x,y,σ)⊗I(x,y)
(1)
多尺度Harris角点二阶矩表示为

(2)
式中:σD=0.7σI;Lx(x,y,σD)和Ly(x,y,σD)分别表示标准差为σD的高斯尺度图像在x,y方向上的微分图像。
位置空间响应值表示为
Corner=det(μ(x,y,σI,σD))-α×trace2(x,y,σI,σD)
(3)
尺度空间响应值表示为
(4)
其中,det表示矩阵的行列式;trace表示矩阵的迹;α是取值于0.04~0.06的参数;Lxx(x,y,σI)和Lyy(x,y,σI)表示图像尺度为σI的尺度空间图像的二阶微分。
若局部特征点的位置空间响应值、尺度空间响应值均大于阈值,并且尺度空间响应值大于相邻两层对应点的尺度空间响应值,那么该点即为检测到的Harris多尺度角点。
由于高斯尺度图像涉及到微分运算,因此采用差分替代微分,利用像素点与差分模板的卷积来实现微分运算,不仅减少了微分运算的计算量,而且卷积更易于FPGA实现。
在程序设计中,选用不同权值的高斯模板来替代高斯函数。标准差σ越大,对应的高斯模板也会越大,但大窗口高斯模板不利于FPGA实时性处理。对于响应值的计算,引入改进的Harris角点响应函数,得到改进的位置空间响应为
(5)
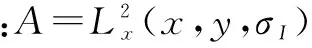
改进后的多尺度Harris角点提取的FPGA实现结构如图2所示,考虑到角点坐标精度和FPGA实现延时情况,前3个尺度图像由原始图像直接与高斯模板卷积得到,后3个尺度图像由前一尺度图像与高斯模板卷积得到。将尺度图像与微分模板相卷积得到微分图像,并计算出尺度空间和位置空间的响应值。最后响应值经FIFO(First Input First Output)缓存对齐并同步输出,同时在尺度空间和位置空间上进行极值点搜索,最终得到图像的多尺度Harris角点。

图2 多尺度Harris角点提取的FPGA实现结构
2.2图像斑点提取
图像斑点是指与周围像素值有着明显区别的区域域中心点,与角点相比,斑点是一个小的区域,因此斑点具有更好的稳定性和抗噪声能力,是一种重要、稳定的特征点。
基于一维高斯函数的二阶导数可以检测一维斑点信号的方法,本文提出采用二维高斯函数的拉普拉斯LoG(LaplaceofGuassian)算子来检测二维图像斑点信号[9]。
二维高斯函数的拉普拉斯算子为
(6)


图3 二维斑点卷积
当高斯函数标准差σ和图像斑点半径R满足σ=R时,黑色斑点边缘产生过零点的位置不会发生变化,并会在斑点中心位置产生一个极大值;同理,当出现白色斑点时,拉普拉斯斑点响应就会出现一个极小值;因此可以通过搜索极大值或者极小值的坐标来确定斑点中心的位置,从而实现二维图像斑点的检测。
由于拉普拉斯算子需要对高斯函数进行二阶求导运算,计算量大、过程复杂,因此对拉普拉斯算子进行改进,以提高FPGA实现的运行速度。
二维高斯函数对标准差σ求导可得
(7)
对比式(6)、(7),可得到
(8)

(9)
因此,位置空间响应值可以表示为

(G(x,y,kσ)-G(x,y,σ))⊗I(x,y)=
G(x,y,kσ)⊗I(x,y)-G(x,y,σ)⊗I(x,y)=
L(x,y,kσ)-L(x,y,σ)
(10)
由于极大值、极小值的位置均是图像斑点的中心位置,因此可以将式(10)作进一步改进,改进后的斑点响应函数如下

(11)
经不同标准差的高斯卷积生成的7个尺度的高斯函数图像,通过FIFO缓存对齐。将相邻两层高斯尺度图像作差替代拉普拉斯响应值的计算,得到6个尺度差值送至极值点搜索模块并搜索极值点,最后确定图像的斑点坐标。
极值点搜索模块的FPGA结构如图4所示,相邻3层尺度为σi-1,σi,σi+1的斑点响应值并行、同步输入到3×3邻域图像生成模块,每层输出9个邻域图像数据。对于σi尺度邻域内的极大值,要保证该点的响应值大于同层领域8个响应值且大于σi-1,σi+1尺度邻域的极大值。在判断σi-1,σi,σi+1尺度邻域内最大值的时候,只需要将前一个时钟的最大值与当前时钟的I13,I23,I33值进行比较,这样可以减少比较次数。

图4 极值点搜索的FPGA实现结构
3 多尺度特征点匹配及其FPGA实现
图像的多尺度特征点匹配利用特征描绘子来描述两个特征点不同邻域内的图像特征,生成相同维数的特征描绘子矢量,通过计算这两个特征描绘矢量的相似度来完成多尺度特征点对的匹配。虽然采用SIFT特征描绘子能取得很好的效果,但描绘复杂、矢量维数高,难以在FPGA上实现。本文对SIFT特征描绘子的生成方式进行改进,基于SIFT特征描绘子在角点及图像斑点附近必存在边缘、梯度变化明显的特点,统计特征点邻域内的梯度直方图来生成16维特征描绘子;同时还对特征点邻域的选择进行改进,不仅降低了描绘子矢量的维数,也更易于FPGA的实现。
由于在半径为3σi邻域范围内集中了大部分高斯函数值,因此以特征点为圆心,3σi为半径的图像邻域对特征点提取影响大,设计时选取半径为6σi范围内的像素值进行梯度幅值和幅角计算。将0°到360°幅角均分成16项,分别累加每一项的梯度幅值作为特征描绘子的坐标,生成16维特征描绘子。由于改进后的半径6σi小于SIFT的半径12σi,特征维数16远小于SIFT的128维,在FPGA上实现起来更简单、速度更快。
在梯度计算时,设特征点所在尺度的高斯平滑图像为Lx, y,Lx, y上每个点的梯度幅值和幅角计算公式如下
(12)
两幅图像的多尺度特征点Pi、Qi的16维特征描绘子分别记为Pi=(ait)、Qi=(bit),其中1≤t≤16,为整数。SSD算法以对应元素差值的平方和来计算相似度,算法表达式如下
(13)
由于梯度计算涉及除法、均方根、反三角函数的运算,用FPGA实现会耗费较多资源,而且反三角函数不能直接用FPGA实现。本文采用CORDIC(Coordinate Rotation Digital Computer) 算法[10],该算法主要是对简单运算进行迭代实现,包括移位与加法运算,非常适合运用FPGA来实现。同时为了保证运算效率,设计了CLA(Carry Look Ahead Adder)加法器,即超前进位加法器,这样就避免了加法运算时等待低位进位消耗的时间。
FPGA实现多尺度Harris角点和斑点匹配时,分别计算两幅图像的多尺度特征点坐标的梯度,并生成特征描绘子矢量,然后对两幅图像的特征描绘子相似度进行计算,从而完成多尺度特征点对的匹配。
4 实验验证
FPGA芯片采用Altera公司的EP3C120F484C7,系统时钟为25 MHz,对花盆、吊兰、玩具3组图像进行测试,均为8位灰度图,分辨率为600×450和450×400,从6个尺度对3组图像进行多尺度特征点提取,分别显示在图5a,5b,5c中。

图5 3组图片的多尺度特征点
上述3组图像的Harris角点和斑点数如表1所示。
表1多尺度Harris角点和斑点提取数目

测试图像尺度1尺度2尺度3尺度4尺度5尺度6角点斑点角点斑点角点斑点角点斑点角点斑点角点斑点总和花盆14453718001214109123吊兰1571431959341603321659493玩具9610413283021615188312
6个尺度进行多尺度Harris角点和图像斑点提取时,尺度不同导致特征点的坐标也不同,因此特征点的数量明显大于单一特征点的数量,特征提取效果好;由于特征点种类不一样,两种方法提取的特征点坐标重合数量极少(吊兰图片重合1个坐标)。将两种方法结合,比单一的多尺度Harris角点和图像斑点检测的特征点数量提高了近1倍左右,更能反映出图像的特征。
对花盆、吊兰、玩具3组图像进行组内匹配,从匹配效果来看,第1组花盆图片123/112个多尺度特征点匹配到71对,匹效果图如图6a所示;第2组吊兰图片492/497个多尺度特征点匹配到192对,如图6b所示;第3组玩具图片312/306个多尺度特征点匹配到115对,如图6c所示。
通过对上述3组图片机型多尺度特征点提取及匹配进行测试,均取得了良好的匹配效果,验证了本设计方法可行,基于FPGA的算法改进合理。
多尺度特征点在匹配时,速度主要与图像的多尺度特征点数量有关。3组图像分别使用FPGA、CPU和GPU实现SIFT算法进行对比测试,采用的FPGA芯片与上相同,CPU采用Inteli5-2430,RAM为4Gbyte,GPU为NVIDIAGeForceGT540M。三者耗时与匹配情况如表2所示。

图6 3组图片的多尺度特征点匹配

测试图片FPGA-改进SIFTCPU-SIFTGPU-SIFT匹配点对数耗时/ms匹配点对数耗时/s匹配点对数耗时/ms花盆7153.08771.712981104吊兰18289.162314.1321257281玩具11571.361382.5369141172
根据表3可知,虽然改进SIFT的匹配点对数与标准SIFT算法相比略有减少,但是16维特征算子算法复杂度比128维SIFT特征算子算法复杂度大大减小。3组图片特征点匹配的CPU实现耗时约为FPGA的32~46倍,GPU实现耗时约为FPGA的2~3倍。
5 结论
本文根据FPGA的特点,结合Harris角点和斑点两种多尺度特征点,对多尺度特征提取与匹配算法进行改进,不仅降低了算法复杂度,而且充分利用了FPGA的并行性,基于FPGA的多尺度特征点匹配速度远远大于CPU实现的速度,优于GPU实现的速度,适用于实时性要求高的场合,且取得较好的匹配效果。
[1]余先川, 吕中华, 胡丹. 遥感图像配准技术综述[J]. 光学精密工程,2013,21(11): 2960-2972.
[2]戴涛,朱长仁,胡树平. 图像匹配技术综述[J]. 数字技术与应用,2012(3): 174-175.
[3]高晶,吴育峰,吴昆,等. 基于角点检测的图像匹配算法[J]. 仪器仪表学报,2013,34(8):1717-1725.
[4]LOWE D G. Distinctive image features from scale-invariant keypoints[J]. International journal of computer version,2004,60(2):91-110.
[5]何婷婷,苪建武,温腊. CPU-GPU协同计算加速ASIFT算法[J]. 计算机科学,2014,41(5):14-18.
[6]杨天天, 鲁云萍, 张为华. 一种基于GPGPU的SIFT加速算法[J]. 计算机技术与应用,2015,41(1):149-152.
[7]王渝,王刚. 基于FPGA的改进Harris角点检测方法[J]. 通信技术,2010,43(4):188-160.
[8]肖得胜,刘桂华. 多尺度Harris焦点检测的FPGA实现[J]. 通信技术,2012,45(11):85-86.
[9]王永明,王贵锦. 图像局部不变特征与描述[M]. 北京:国防工业出版社,2010:129-166.
[10]刁玉,宋泽琳,马令坤. 基于FPGA的CORDIC 算法的改进及实现[J]. 微型机与应用,2011,30(16):78-81.
刘桂华(1972— ),女,博士,教授,主要研究方向为机器视觉、图像处理;
陈林宇(1989— ),硕士生,主研图像处理;
肖得胜(1986— ),硕士生,主研图像处理。
责任编辑:闫雯雯
Multi-scale feature points extraction and matching of images based on FPGA
LIU Guihua,CHEN Linyu,XIAO Desheng
(SchoolofInformationEngineering,SouthwestUniversityofScienceandTechnology,SichuanMianyang621000,China)
In view of some problem such as limited exacted feature,high algorithm complexity and slow processing speed existed in multi-scale feature points extraction and matching of images,a method is presented,which combines the techniques of capturing feature points of intersection of object boundary in an image by using multi-scale Harris corner detection algorithm and detecting 2D image spot signal by Laplace of Gaussian, and completing matching of feature points by similarities of SIFT feature descriptor. The algorithm complexities of multi-scale Harris corner detection algorithm, spots extraction method and SIFT feature descriptor’s generation method has been greatly reduced to realize in FPGA to achieve fast speed based on parallel characteristics of FPGA. The experiments demonstrate that these techniques can achieve faster speed than the software implementation method with few image feature points loss.
FPFA;multi-scale;Harris corner;gradient;SIFT
TP391
A
10.16280/j.videoe.2016.09.021
四川省教育厅重点项目(14ZA0090);西南科技大学重点实验基金项目(13zxtk05);校创新团队基金项目(14tdtk01)
2015-10-21
文献引用格式:刘桂华,陈林宇,肖得胜. 基于FPGA的图像多尺度特征点提取及匹配[J].电视技术,2016,40(9):103-107.
LIU G H,CHEN L Y,XIAO D S. Multi-scale feature points extraction and matching of images based on FPGA[J]. Video engineering,2016,40(9):103-107.
