MRAC在位置随动控制系统中的应用

王志翔，王竹平

(1.上海理工大学 光电信息与计算机工程学院，上海 200093；2.上海辰竹仪表有限公司，上海 201612)



MRAC在位置随动控制系统中的应用

王志翔1，王竹平2

(1.上海理工大学 光电信息与计算机工程学院，上海 200093；2.上海辰竹仪表有限公司，上海 201612)

针对位置随动控制系统具有不确定性的特点，设计了具有良好跟随性的自适应控制系统。利用机理法建立数控机床刀具进给定位控制系统的数学模型，将该系统等效为带有参变量的单输入单输出系统，在该模型的基础上设计了基于李雅普诺夫稳定性理论的模型参考自适应控制系统。利用Matlab进行仿真，其仿真结果表明，基于李雅普诺夫稳定性理论的模型参考自适应控制系统具有良好的跟随性、稳定性和控制精度。

位置随动控制系统；数控机床；李雅普诺夫稳定性；模型参考自适应控制；Matlab仿真

数控机床刀具进给定位控制系统可视为一种典型的位置随动控制系统，广泛应用于机械制造、冶金、船舶及航天航空等领域。系统本身具有一定的不确定性，当改变控制系统输入信号时，要求输出对输入具有良好的跟随性。传统的控制理论，要求建立精确的被控对象模型，当系统参数或环境变化较大时，传统的控制理论存在较大的局限性，无法取得良好的控制效果。

自适应控制系统的设计思想是：系统在运行过程中，本身能不断检测其性能和参数，从而了解系统当前的运行指标，并与期望的指标进行比较，同时做出决策来改变控制器的结构、参数，使控制器主动去适应系统或环境的变化，以保证系统运行在最佳的状态。模型参考自适应控制系统是目前理论上较成熟且应用广泛的一类自适应控制系统。本文针对典型的位置随动控制系统，即数控机床刀具进给定位控制系统的数学模型，设计基于李雅普诺夫稳定性理论的模型参考自适应控制(Lyapunov-MRAC,ModelReferenceAdaptiveControl)系统，并通过Matlab进行仿真，仿真结果表明基于Lyapunov-MRAC系统能有效提高数控机床刀具进给定位控制系统的控制精度、抗干扰能力以及自适应能力。

1　数控机床控制系统数学模型

在数控机床刀具进给定位控制系统中，刀具进给速度主要通过伺服电机进行控制，系统可简化为一个双闭环的位置随动控制系统。内环是伺服电机的角位移反馈，外环是数控机床执行机构的位移反馈，系统的输入、输出量均是角位移，且输入量是不断变化的，其要求输出量能按较高的精度跟随输入量的变化而变化，主要是解决具有一定精度的位置跟随问题。所以整个系统由位置给定、电位器、放大器、伺服电机、测速发电机、位置传感器构成，系统框图如图1所示。

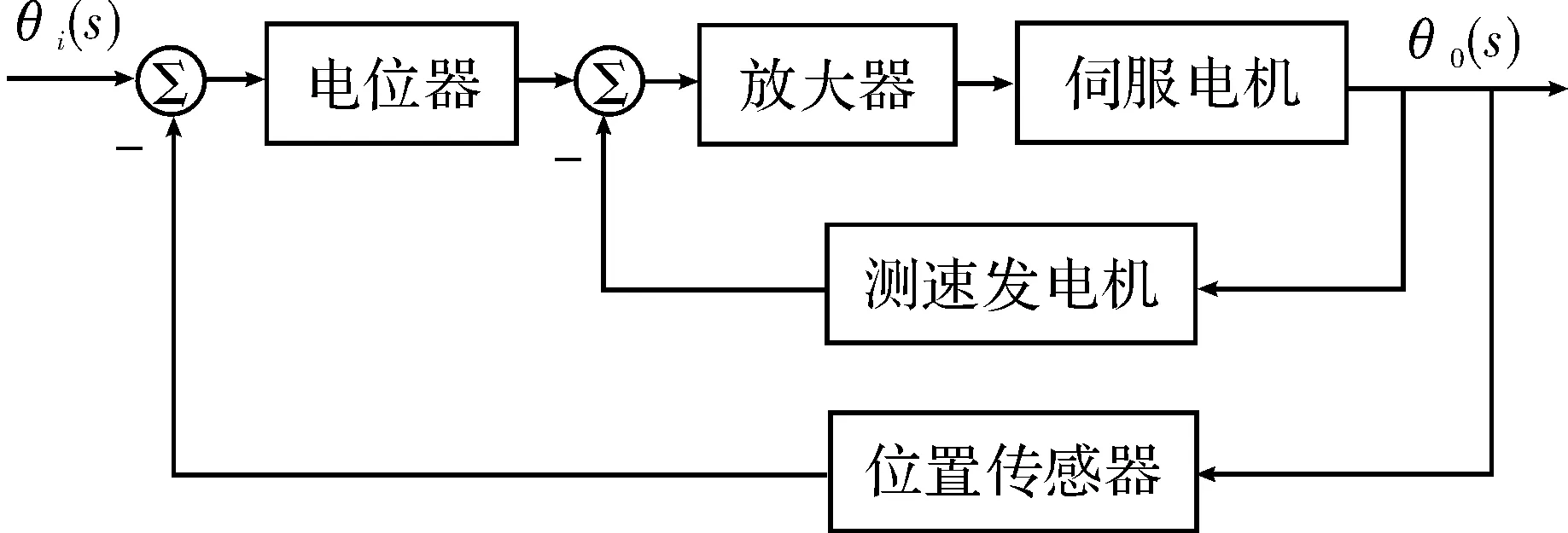
图1　数控机床刀具进给定位控制系统方框图

电位器是一种将线位移或角位移变换为电压量的装置，比例系数K0为0.8；放大器将比较元件给出的偏差信号进行放大用来推动执行元件，增益K1为3；测速发电机用来反馈伺服电机的角位移，比例系数Kt为0.12；位置传感器用来反馈数控机床执行机构的位移，增益为1；伺服电机作为执行机构用来控制被控对象的机械运动，传递函数可简化为

(1)

其中，伺服电机的时间常数Km为2.5;伺服电机的传递系数Tm为0.1。系统对应的结构如图2所示。

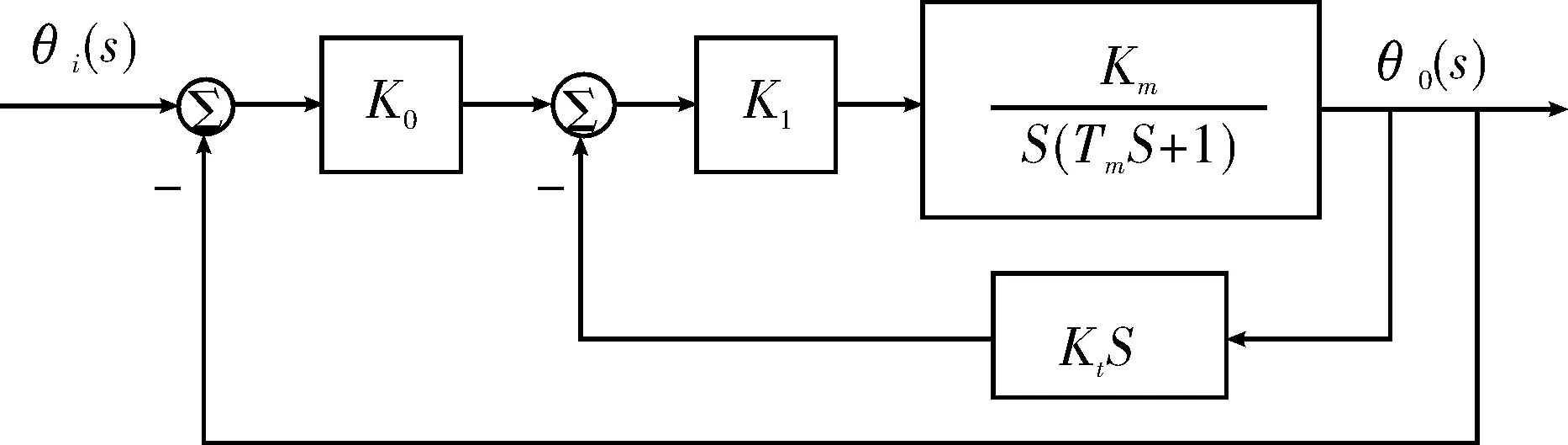
图2　数控机床刀具给进定位控制系统结构图

由结构图可得闭环系统的传递函数为

(2)

将各系数代入式(2)可得

(3)

系统在实际运行中，会产生一些非线性、不确定性因素，例如测量元件、放大器及执行机构的不灵敏区造成的死区特性；或输入信号突然发生较大变化等。由于非线性系统可表示在线性系统的输入端或输出端加入非线性环节。鉴于此，采用简单的折线代替实际的非线性曲线，将非线性特性典型化，而由此产生的误差一般处于工程所允许的范围内[1]。定义非线性环节输出和输入的比值为变增益Kp，可得等效传递函数

(4)

2　Lyapunov-MRAC系统设计

模型参考自适应控制的目的是使系统的实际输出渐近一致地跟随参考模型的输出，使被控系统的动态特性满足要求，即使得广义误差信号渐近一致地收敛于零。基于Lyapunov-MRAC系统是通过调节可调系统的增益来实现系统实际输出与参考模型输出相减得到的广义误差信号趋向于零，并可保证闭环控制系统的稳定性，故又称为可调增益Lyapunov-MRAC。系统由参考模型、控制器、被控对象和自适应机构组成，系统结构如图3所示。设计内容包括设定参考模型，实现参考模型与基本回路的性能比较，进行自适应规律以及可调控制器设计。G(s)为理想的传递函数作为参考模型，KpG(s)为变增益的实际传递函数，Kc(t)为可调控制器的可调增益。

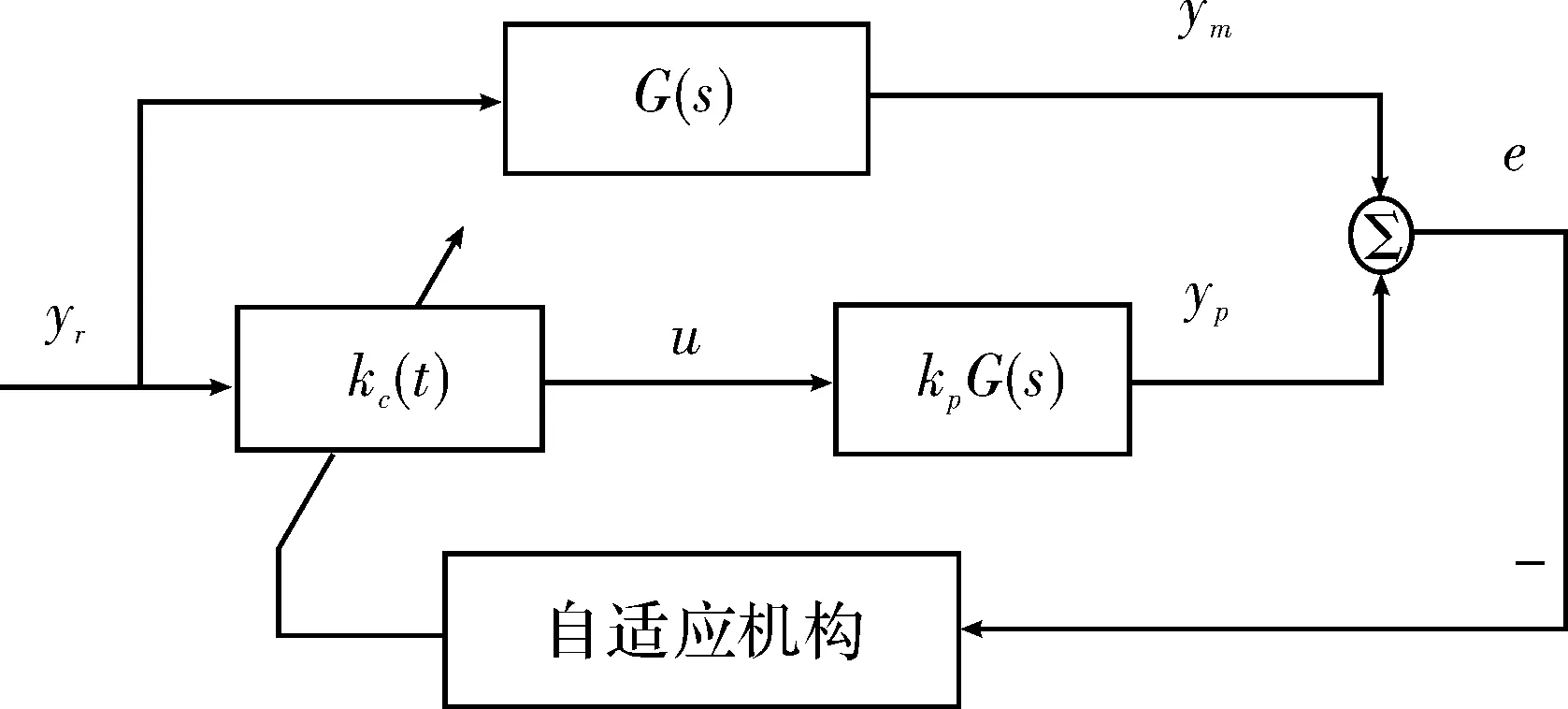
图3　基于Lyapunov-MRAC系统结构图

由图3可知

e(t)=ym(t)-yp(t)

(5)

e(t)=[1-Kc(t)Kp]G(s)yr(t)

(6)

令k=1-Kc(t)Kp，得

e(t)=kG(s)yr(t)

(7)

将传递函数转化为状态空间可观测规范型

e=cx

(8)

ATP+PA=-Q

(9)

选择Lyapunov函数V=γ′xTPx+k2，γ′>0，则有

(10)

由式(8)，式(9)得

(11)

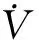
(12)

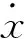
由上述引理可知，若系统传递函数G(s)为严格正实函数，则由上述各式可得可调增益Lyapunov-MRAC自适应律

(13)

式中，γ=γ′/kp>0为自适应增益。

由图3可知，基于Lyapunov-MRAC系统的自适应控制律为u(t)=kc(t)yr(t)[2]。

3　Lyapunov-MRAC算法程序设计

按照上述推导的计算方法，得到基于Lyapunov-MRAC算法如下：

步骤1选择参考模型，可将理想的被控对象传递函数模型作为参考模型；

步骤2设定输入信号yr(t)和自适应增益γ；

步骤3采样当前参考模型输出ym(t)和系统实际输出yp(t)；

步骤4计算自适应控制律u(t)；

步骤5返回步骤3，继续循环。

基于Lyapunov-MRAC系统算法对应的程序流程图，如图4所示。

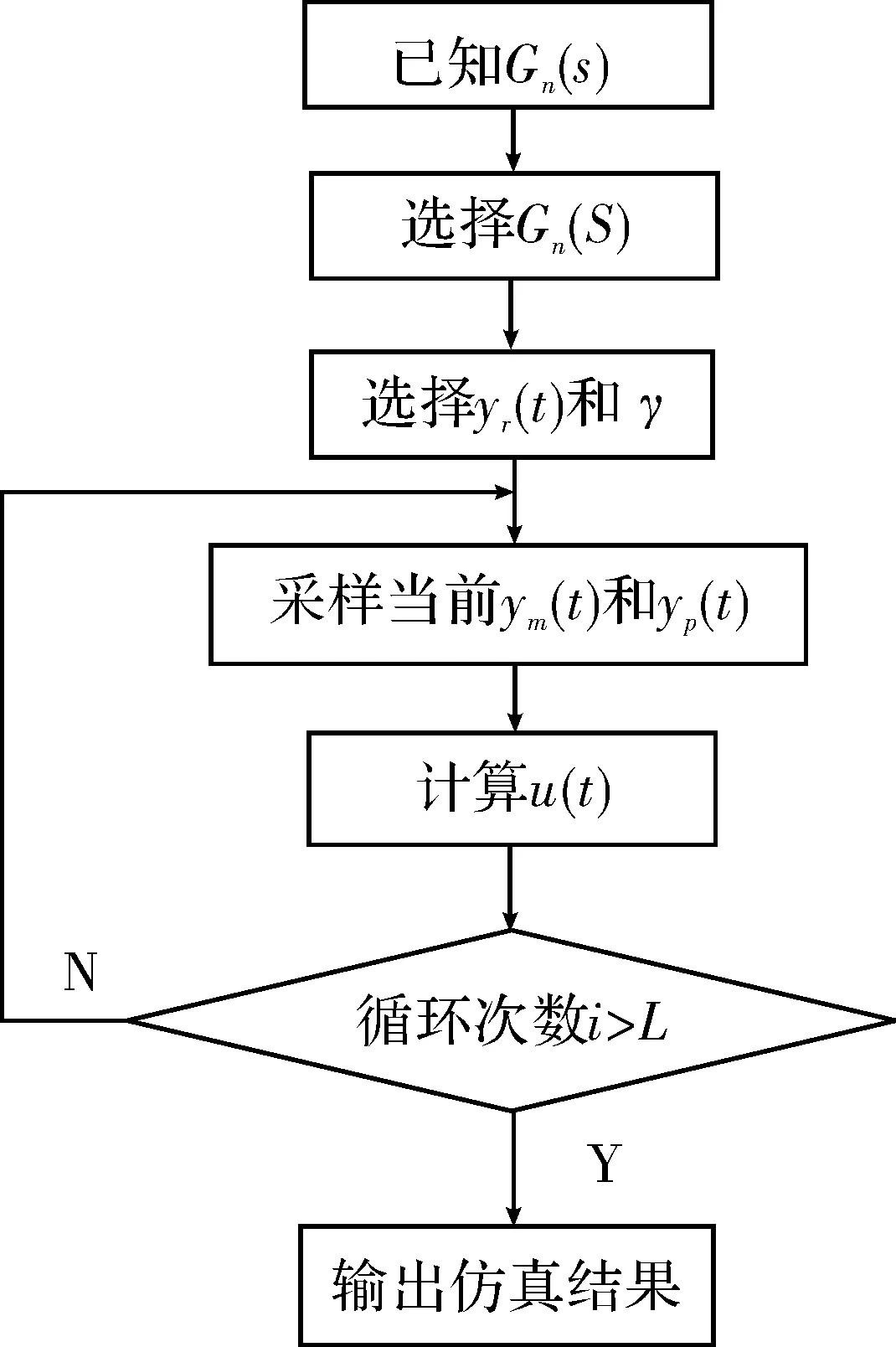
图4　基于Lyapunov-MRAC算法程序流程图

4　仿真结果及分析

数控机床刀具进给定位控制系统的输入信号一般具有周期性变化的性质，可选择正弦信号作为系统的输入信号

yr(t)=Asin(ωt+φ)=sin(0.1πt)

(14)

理想情况下，忽略系统中的非线性因素，系统模型参数保持不变，仿真研究时取Kp为1。输入yr(t)、参考模型输出ym(t)、被控对象输出yp(t)如图5所示，控制量u(t)、误差信号e(t)如图6所示；若非线性因素不可忽略，例如输入信号突变，或系统工作状态靠近测量元件、放大器不灵敏区造成的死区，导致系统模型参数变化较大，仿真研究时取Kp为0.6。输入yr(t)、参考模型输出ym(t)、被控对象输出yp(t)如图7所示；控制量u(t)、误差信号e(t)如图8所示。

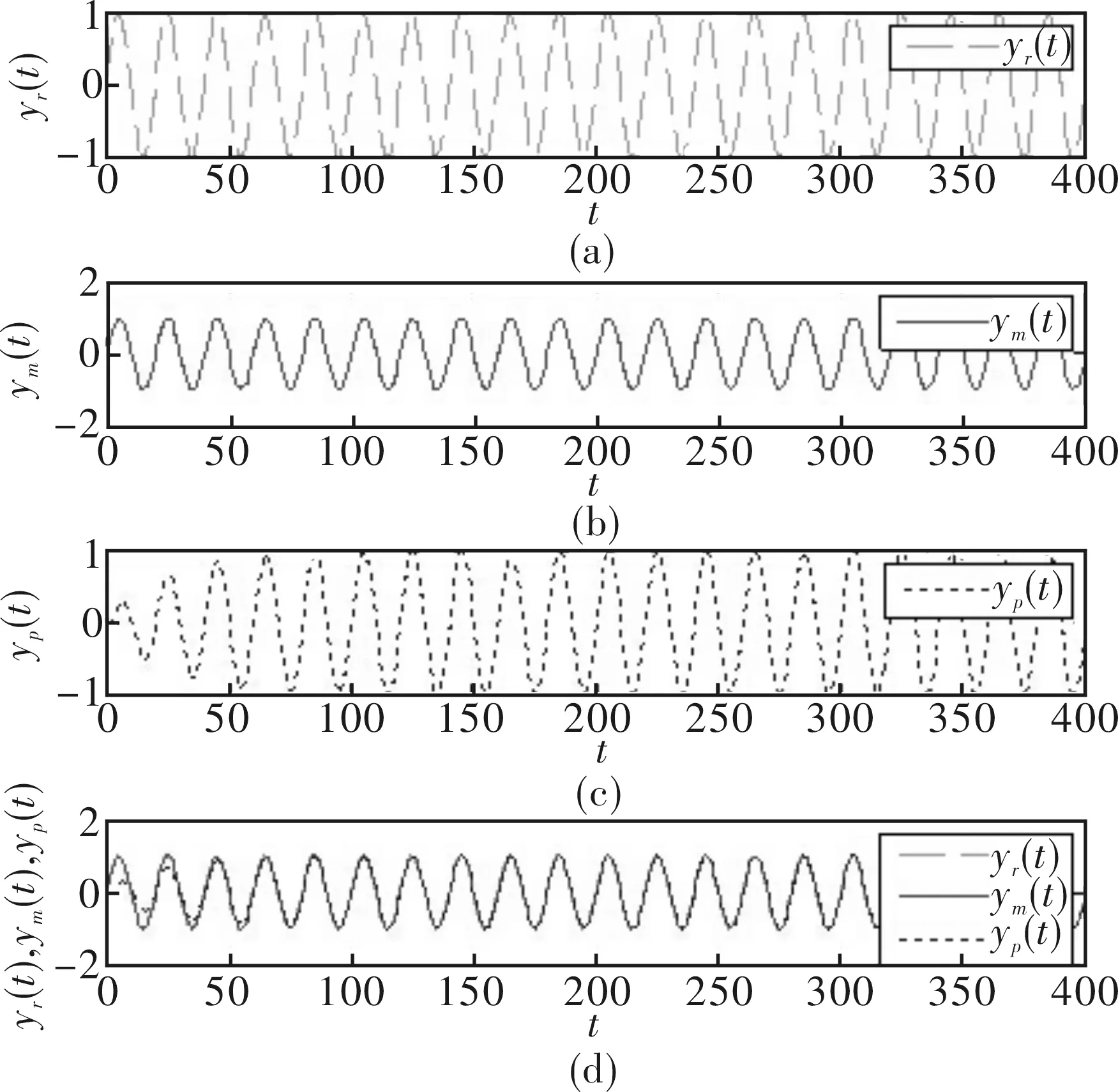
图5　Kp为1时,yr(t)、ym(t)、yp(t)曲线

图6　Kp为1时,u(t)和e(t)曲线

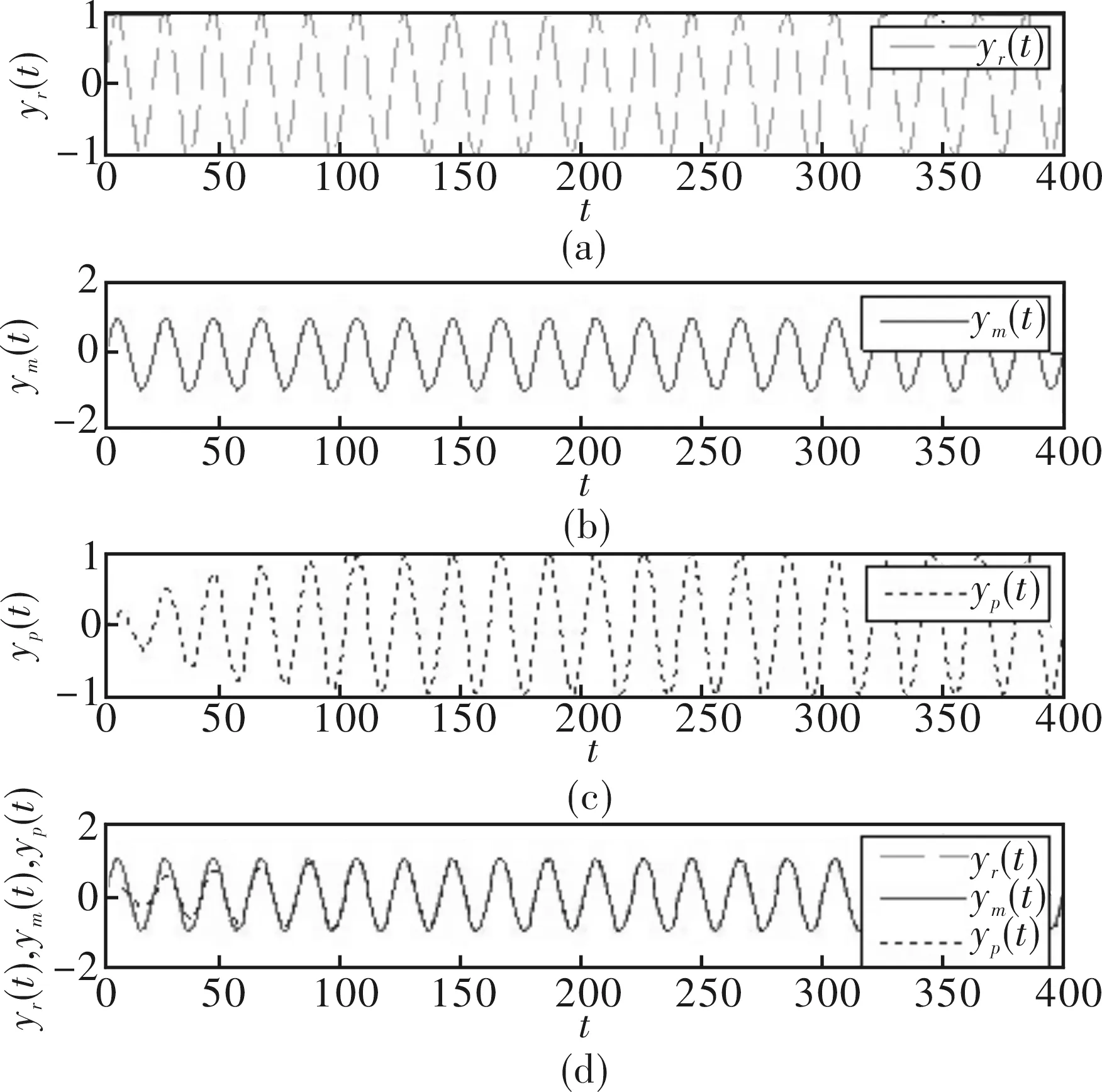
图7　Kp为0.6时,yr(t)、ym(t)和yp(t)曲线

比较上述仿真结果图可知，无论是在理想工作环境下，还是由于不确定或非线性因素导致系统模型参数发生较大变化时。基于Lyapunov-MRAC系统中输出信号均能以较高的精度跟随输入信号而变化，并经过一段时间的过渡后，输出信号与输入信号基本达到完全一致，使得误差信号e(t)趋近与零。说明基于Lyapunov-MRAC系统能获得较高的控制精度、良好的跟随性与稳定性。

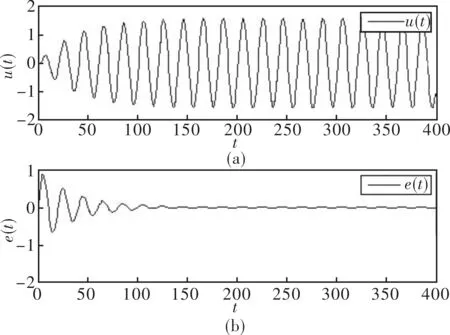
图8　Kp为0.6时,u(t)和e(t)曲线图

5　结束语

本文通过建立数控机床刀具进给定位控制系统的数学模型。在此模型的基础上，设计了基于Lyapunov-MRAC系统。利用Matlab仿真软件对基于Lyapunov-MRAC算法系统进行仿真研究。仿真结果表明，对于不确定性、模型参数可变的被控系统，基于Lyapunov-MRAC系统仍具有较好的控制精度、抗干扰能力

和自适应能力，这对实际中的工业应用具有重要的现实意义。

[1]胡寿松.自动控制原理[M].4版.北京:科学出版社科,2005.

[2]庞中华,崔红.系统辨识与自适应控制Matlab仿真[M].北京:北京航空航天大学出版社,2009.

[3]刘兴堂.应用自适应控制[M].西安:西北工业大学出版社,2003.

[4]李元春.计算机控制系统[M].2版.北京:高等教育出版社,2009.

[5]刘豹,唐万生.现代控制理论[M].3版.北京:机械工业出版社,2011.

[6]周开利,邓春晖.Matlab基础及其应用教程[M].北京:北京大学出版社,2007.

[7]刘金琨.先进PID控制Matlab仿真[M].3版.北京:电子工业出版社,2011.

[8]Katsuhiko Ogatako.控制理论Matlab教程[M].王诗宓,王峻,译.北京:电子工业出版社,2012.

[9]刘楚辉.自适应控制的应用研究综述[J].组合机床与自动化加工技术,2007(1):1-4.

[10]逢启寿,肖顺根,宋萌萌.数控机床切削加工过程的模型参考自适应控制研究[J].机床与液压,2009,37(3):53-55.

Application of MRAC in the Position Servo Control System

WANGZhixiang1,WANGZhuping2

(1.SchoolofOptical-ElectricalandComputerEngineering,UniversityofShanghaiforScienceandTechnology,Shanghai200093,China; 2.ShanghaiChenzhuInstrumentCo.,Ltd.,Shanghai201612,China)

Amodelreferenceadaptivecontrolsystemwitchofgoodfollowingcharacteristicsisdesignedfortheuncertaintyofthepositionservosystem.ThemodelofnumericalcontrolmachinesystemisdiscussedwiththeuncertainsystemequivalenttotheonewithparametricvariablesingleinputandsingleoutputtoestablishaLyapunov-MRAC(ModelReferenceAdaptiveControl)system.TheMatlabsimulationresultsshowthattheLyapunovMRACsystemhasgoodfollowingcharacteristics,stabilityandprecision.

positionservosystem;numericalcontrolmachine;lyapunovstability;modelreferenceadaptivecontrol;Matlabsimulation

2015- 12- 24

王志翔(1990-)，男，硕士研究生。研究方向：智能控制技术与仪器仪表。

10.16180/j.cnki.issn1007-7820.2016.09.009

TP273

A

1007-7820(2016)09-030-04