基于改进WFPSO算法的无刷直流电机模型分析

徐晓冬，戴曙光

(上海理工大学 光电信息与计算机工程学院，上海 200093)



基于改进WFPSO算法的无刷直流电机模型分析

徐晓冬，戴曙光

(上海理工大学 光电信息与计算机工程学院，上海 200093)

针对传统的无刷直流电机控制无法在线调整参数、难以精确控制的问题，提出一种基于改进的粒子群优化(PSO)算法的模糊PID控制器设计。通过对粒子群优化算法的参数进行分时段更新，实现模糊PID控制器参数动态全局优化，来确定使用双闭环控制模型的无刷直流电机的最优参数。Matlab仿真结果表明，该研究方法较传统方法可使得转速无超调、减少调节时间，同时启动时转矩脉动较小。

粒子群优化；模糊PID控制器；无刷直流电机；Matlab

无刷直流电机(BrushlessDirectCurrentMotor,BLDCM)是一种无换向电刷机械构造而直接使用电子换向器的新式电机。具有无换向火花、能获取更高的扭矩转速特性、高速动态响应、效率高、寿命长、低噪声和易于控制维护等特点，广泛应用于计算机、航空、医学及消费电子领域，工业机器人以及精密电子仪器的驱动中都有其应用[1-3]。

尽管BLDCM结构简单，但也是一种复杂多变量、耦合、非线性的系统，传统PID控制无法达到动态性和鲁棒性的要求[3]。而模糊智能控制具有变参数、非线性、自寻优等优点，可较好地适应BLDCM调速系统的变结构和非线性等因素，进而提高整个BLDCM调速系统的鲁棒性[3]。

实现无刷直流电机控制模型，文献[4]对标准PSO算法进行分析，但未对参数做调整；文献[5]采用模糊PID的电机仿真模型，不可以在线动态调整参数；文献[6]采用双闭环控制，速度环采用改进PSO算法优化传统PID控制的参数，电流环采用滞环电流控制。本文结合其优点，采用双闭环结构，对PSO的参数进行分时段更新，在模糊PID控制上加入改进的WFPSO算法优化BLDCM的运行性能，即优化模糊PID控制器的3个参数kp、ki、kd，并通过Matlab的Simulink仿真工具对BLDCM控制系统进行仿真，实时跟踪模糊PID控制器的参数变化，通过分析比较转速、转矩等参数，验证结果的可行性。

1　无刷直流电机数学模型

无刷直流电机的定子为绕组，转子为永磁体[7]。定子产生磁场使转子转动，霍尔传感器检测转子位置作为换相信号。根据换相信号，功率开关电路产生对应的逻辑动作，在绕组中产生逆变交流信号，通过气隙形成旋转磁场，带动转子连续不断地旋转。因此，无刷直流电机与永磁直流电机不同，无需电刷，而是用永磁体代替电枢绕组。本文研究以星形连接的三相两极无刷直流电机为例，式(1)～式(4)[7]描述了无刷直流电机的电压平衡方程和运动方程

(1)

vemf=Kb·ω(t)

(2)

T(t)=kt·i(t)

(3)

(4)

其中，vapp(t)为供电电压；ω(t)为电机转速；L为定子的电感；i(t)为电路中电流；R为定子电阻；vemf是反电动势；T(t)为电动机的转矩；D为粘滞系数；J为转动惯量；kt为电动机转矩常数;kb为反电动势常数。

2　改进的粒子群优化算法

粒子群优化算法(Particle Swarm Optimization, PSO)是由Eberhart博士和Kennedy博士创造的一种新的全局优化进化算法，源于对鸟群捕食的行为研究[8]。

2.1标准粒子群算法数学模型

PSO算法对生物种群的行为特征出发，对聚集在D维空间中的粒子进行模拟。对于每个粒子i，都有一个D维位置向量xi=(xi1,xi2,…,xiD)和一个D维速度向量vi=(vi1,vi2,…,viD)，粒子i以速度vi搜索解空间时，保存搜索到的最优经历位置pi=(pi1,pi2,…,piD)。在每次迭代开始时，粒子都会根据自身惯性和经验及群体最优经历位置pg=(pg1,pg2,…,pgD)来调整自身的速度向量以调整自身位置。算法流程如图1所示。

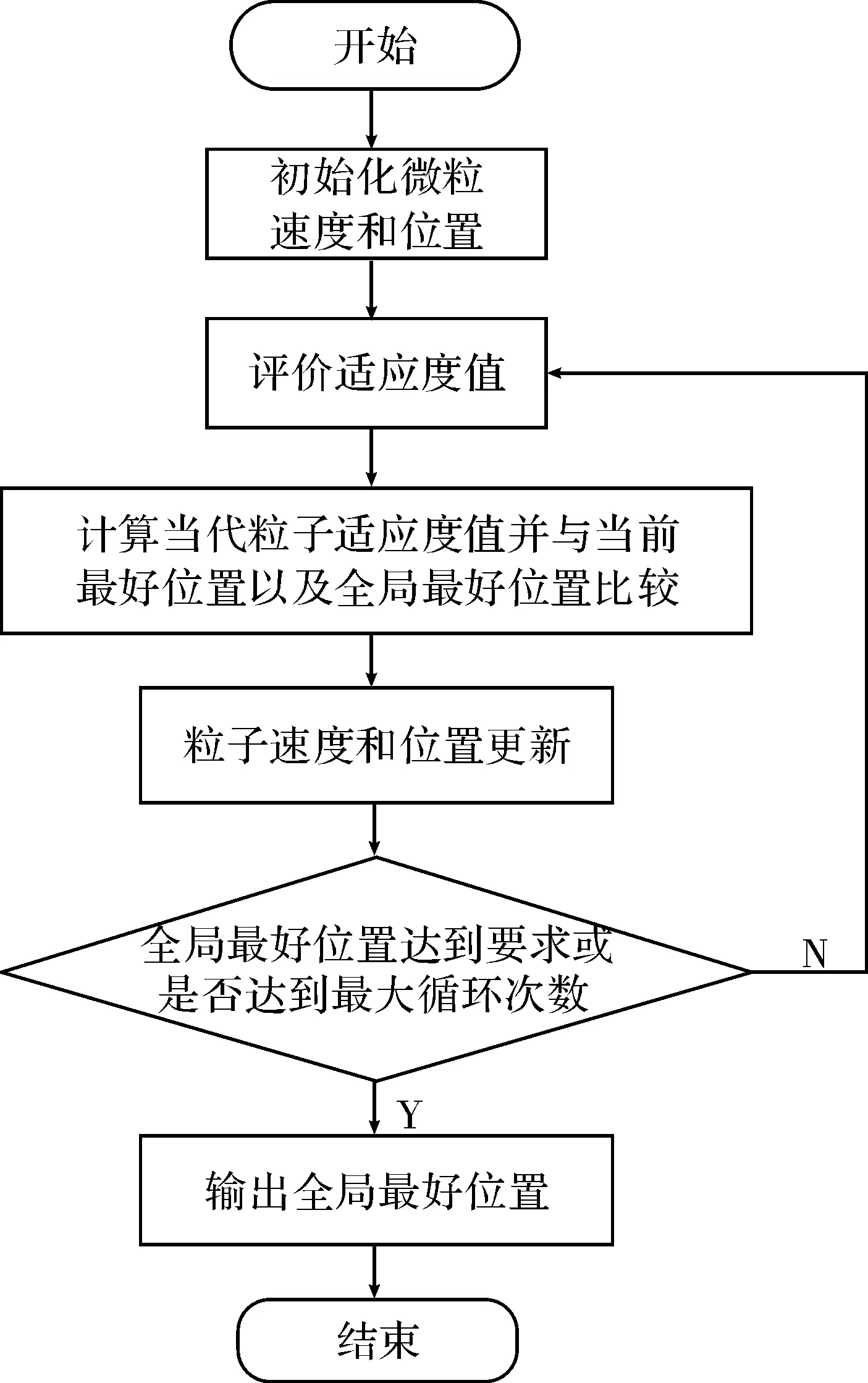
图1　标准PSO算法流程图

每个粒子的位置和速度更新如下[9]

(5)

(6)

其中，c1、c2是正常数，称为加速因子；r1、r2为随机数，在[0,1]均匀分布；d为D维空间中的子维数；ω为惯性权重因子。

式(5)由3部分组成，第一部分是粒子初始速度，其值越大，越利于全局搜索，其值越小，越利于局部搜索；第二部分是粒子利用积累的经验，通过c1、r1的随机调整，使粒子具有较强的全局搜索能力，避免陷入局部极小；第三部分表明粒子间信息共享和社会协作，通过c2、r2的随机调整，学习其他粒子经验。在这3个部分的共同作用下，粒子根据自己的经验并学习种群经验，不断调整自身速度与位置，从而有效地搜索出全局最优位置。

2.2改进的WFPSO算法

对于PSO算法的参数调整，文献[9]提出了基于惯性权重和分段时变学习因子的PSO算法，即WFPSO算法[9]。本文在WFPSO算法的基础上，根据种群的数量进行分段更新加速因子和惯性权重因子。算法的惯性权重因子的更新如式(7)

(7)

其中，ωmax为最终权重；ωmin为初始权重；itermax为最大迭代次数；iter为当前迭代次数。在迭代初期，使用较大的ω，使得粒子能够较快地全局收敛，随着迭代次数的增加，惯性权重ω应逐渐减小，在迭代后期能尽快局部收敛。

当iter≤itermax/2时，速度更新如下

(8)

且iter>itermax/2时，速度更新如下

(9)

其中，c1f，c1i，c2f，c2i分别为c1、c2的初始值和终值。

对于粒子群算法的参数c1和c2，设置较大的c1值，会使粒子收敛于局部最优；设置较大的c2值会使粒子过早收敛于局部最大值[10]。因此，式(8)和式(9)中所表示的是在前期迭代时，将c1的值保持最大值，将c2的值线性递增，使粒子尽可能发散至搜索空间；在迭代次数大于总群数目的一半时，使得c1值线性递减，c2保持最大值，增强粒子向全局最优点收敛的能力。

3　BLDCM模糊控制模型

本文通过Matlab的Simulink仿真工具对BLDCM控制系统进行仿真，采用双闭环控制方案，速度环采用模糊PID控制，并加入改进的WFPSO算法动态优化模糊PID控制器参数；电流环直接进行采样形成负反馈，并采用传统PI控制器进行调节。图2为建模的双闭环系统原理框图。

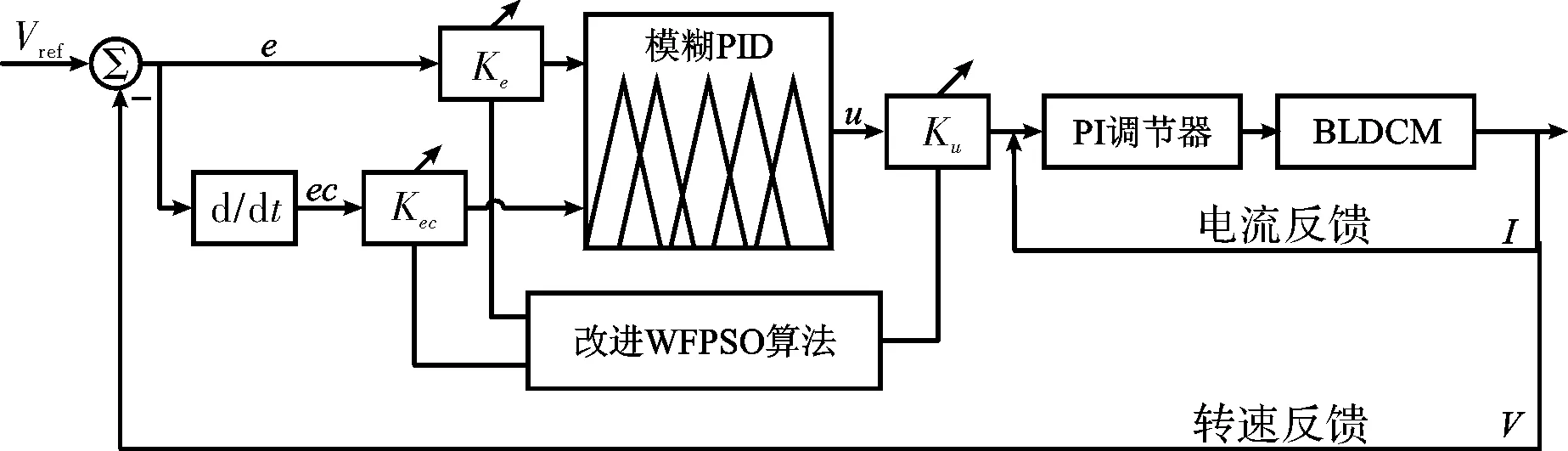
图2　BLDCM双闭环系统原理示意图

图3为BLDCM仿真模型在Simulink中的总体设计控制图，其中包括电机本体主回路模块，逻辑换相模块，逆变器模块，电流采样模块和速度控制模块。其中，电流采样模块使用S函数实现，经采样后送入PI控制器模块形成负反馈；速度控制模块采用子系统形式，如图4所示。由改进WFPSO算法模块和模糊PID控制器组成，子模块的输入为目标速度和实际速度的负反馈值，经过改进的WFPSO算法动态优化模糊PID控制器的kp、ki、kd，再将全局优化后的结果与采样到的电流构成负反馈而形成电流环，由此构成BLDCM的双闭环系统，并在线调整其参数，使得超调量、调节时间达到最优，做到精确控制。

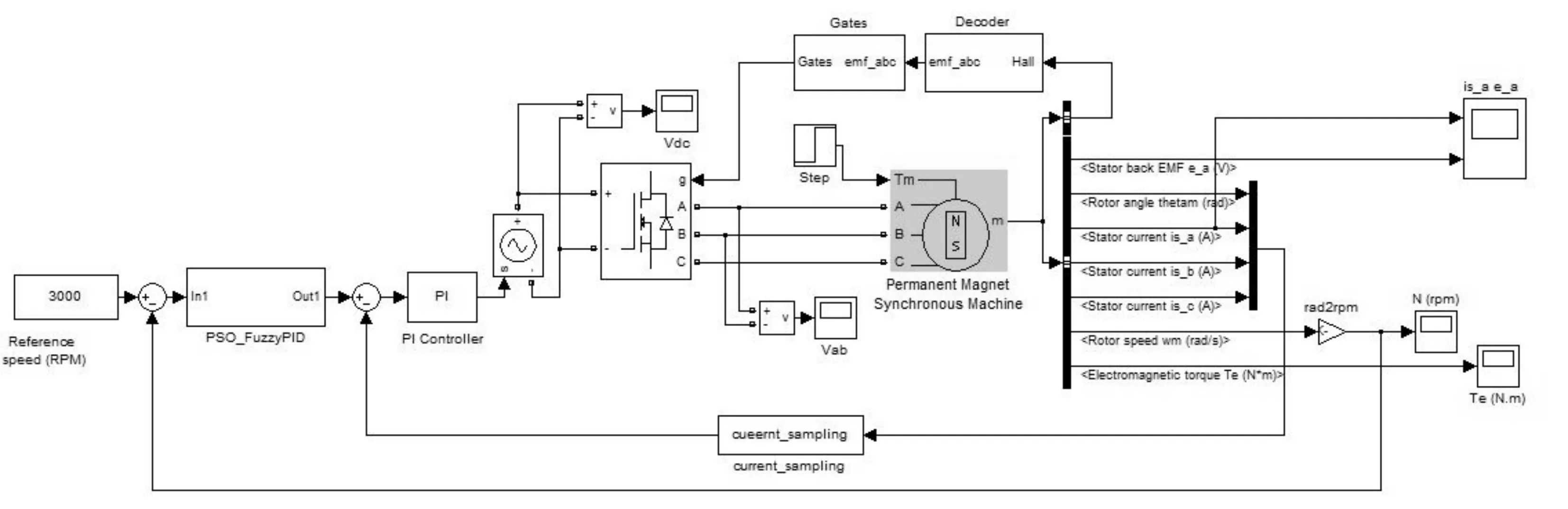
图3　BLDCM仿真模型的总体设计控制图

图4　速度控制模块

4　仿真结果分析

在Matlab R2014a且在Windows 64位系统环境下建立上述模型，无刷直流电机的参数做如下设置：供电直流电压V=500 V，额定转速为3 000 r/min，绕组电阻R=2.875 Ω，有效电感L=8.5×10-3H，转动惯量J=0.8×10-3kg·m2，转矩常数1.4 N·m/A，仿真时间为0.2 s。采样时间Ts=5×10-5s，使得仿真模型更接近实际系统。

仿真分别采用常规PID控制器、WFPSO算法优化模糊PID控制器和加入改进WFPSO算法的模糊PID控制器的BLDCM模型进行仿真。

图5为3种控制器下的转速响应曲线。可以看出，常规PID的转速响应有超调，超调量为6%，且在0.06 s以后进入稳态；使用WFPSO优化模糊PID控制器的方法也有超调，超调量为4.2%，且在0.06 s以后进入稳态，但使用改进后的WFPSO算法应用到速度环，系统无超调，且在0.05 s后进入稳态。因此，无论是在响应速度上还是超调量大小上，加入改进WFPSO的算法的模糊PID控制器都要优于前两种形式，且对转矩变化响应快速。

图6所示的电机转矩曲线中，转矩突变的峰值分别为50.06 N·m、25.68 N·m和22.23 N·m，可以得出，加入改进WFPSO算法的模糊PID控制器的优化方法在启动时转矩脉动较小，且转矩发生突变时变化较平缓。

图5　单位阶跃输入下的转速响应曲线

图6　电机转矩曲线

本文比较研究了使用改进WFPSO优化的模糊PID控制器与WFPSO算法和常规PID控制器对无刷直流电机系统的性能影响。通过对无刷直流电机仿真，仿真结果表明，本文所讨论的控制器可执行实现有效的搜索最优增益的模糊PID控制器参数，通过改进的WFPSO算法，可以更好地提高系统的动态性能和稳态性能。

[1]戴莹.基于BP神经网络的无刷直流电机PID控制方法的研究[D].合肥:合肥工业大学,2007.

[2]程声烽,程小华,杨露.基于PSO-BP神经网络的无刷直流电机模型及控制系统研究[J]. 微电机,2014(8):44-47.

[3]侯春杰.基于遗传算法的无刷直流电机自适应模糊控制[D].洛阳:河南科技大学,2013.

[4]代睿.基于PSO算法的无刷直流电机自适应PID控制研究[J].贵州师范大学学报:自然科学版,2012(1):73-76.

[5]陆华颖,程光伟,陈凯.模糊PID双闭环直流电机调速系统仿真[J].电子科技,2011, 24(10):56-58.

[6]付光杰,杨帛润,高俊莹.基于改进粒子群算法的无刷直流电机控制研究[J].组合机床与自动化加工技术,2013(6):95-98.

[7]Ibrahim H E A,Hassan F N,Shomer A O. Optimal PID control of a brushless DC motor using PSO and BF techniques[J].Ain Shams Engineering Journal,2013,5(2):391-398.

[8]祁春清,宋正强.基于粒子群优化模糊控制器永磁同步电机控制[J].中国电机工程学报,2006,26(17):158-162.

[9]杨帛润.基于改进的神经网络无刷直流电机控制的研究[D].大庆:东北石油大学,2013.

[10]刘家兵.改进粒子群算法及其在模糊控制器设计中的应用[D].兰州:兰州理工大学, 2009.

Analysis of model for Brushless DC Motor Based on Improved WFPSO Algorithm

XUXiaodong,DAIShuguang

(SchoolofOptical-ElectricalandComputerEngineering,UniversityofShanghaiforScienceandTechnology,Shanghai200093,China)

Animprovedparticleswarmoptimization(PSO)algorithmisputforwardfortheprecisecontrolofBrushlessDCMotorbyadjustingtheparametersonline.Theupdatedparametersofparticleswarmoptimization(PSO)algorithmisusedtodynamicallyoptimizetheparametersofthefuzzyPIDcontroller,whichdeterminestheoptimalparametersofdoubleclosedloopcontrolmodeloftheBrushlessDCMotor.ThesimulatedresultsofMatlabshowthatthemethodeffectivelydecreasestheadjustingtimewithoutovershootofspeedwithsmallerstartingtorqueripple.

PSO;fuzzyPIDcontroller;BLDC;Matlab

2015- 12- 10

徐晓冬(1991-)，男，硕士研究生。研究方向：嵌入式系统等。戴曙光(1957-)，男，教授，博士生导师。研究方向：工业光电检测技术与装置等。

10.16180/j.cnki.issn1007-7820.2016.09.011

TP301.6

A

1007-7820(2016)09-037-04