融合改进蚁群和粒子群算法的路径搜索应用

杜　博，夏春蕾，戴曙光

(上海理工大学 光电信息与计算机工程学院，上海 200093)



融合改进蚁群和粒子群算法的路径搜索应用

杜博，夏春蕾，戴曙光

(上海理工大学 光电信息与计算机工程学院，上海 200093)

针对车辆路径搜索对其计算质量和效率要求较高问题，且原始蚁群算法和标准粒子群算法均存在局部优先解、停滞以及收敛速度较慢等缺陷，提出一种融合改进的蚁群和粒子群路径搜索算法。在融合算法前期提高粒子群算法收敛速度，利用其进行粗搜索，后期利用改进的蚁群算法进行细搜索。通过仿真分析表明，融合后的改进算法在路径规划和计算效率上均有较大提升。

路阻模型；融合算法；路径搜索；仿真分析

随着中国城市化进程速度加快，汽车保有量与城市道路设施比例失衡导致的城市交通问题日益突出，目前已成为制约众多城市经济发展的重要因素[1]。因此，为缓解城市交通问题，如何运用现代化信息手段提高城市道路设施资源利用率已成为众多行业学者的研究热点之一[2]。文中从车辆出行路径规划着手，改进融合蚁群算法。通过分析蚁群算法和粒子群算法各自特点，将两个算法进行融合，形成融合型算法。并根据路径搜索问题对蚁群算法和粒子群算法进行针对性改进，采用图论实验对改进后的混合算法进行仿真，证明融合算法在求解准确度和效率上均略有提升。

1　建立城市道路和路阻函数

为更加真实的抽象描述实际道路情况，需要对道路路网建立合适的路阻函数模型。合理的动态路阻权值模型不仅是对实际城市路网中车辆通行力的准确表达，更是后续检验路径搜索能力和提供较优出行决策的前提。目前路阻模型中较为典型的有BPR模型、Davidson模型、TRRL模型等[2-3]，此处以具有代表性的BPR路阻模型结合国内城市交通情况，提出了如下道路和路阻模型

t(q)=t0[1+α1(q1/c1)β1+α2(q2/c2)β2]

(1)

其中，q1、q2分别表示机动车和非机动车的流量；c1、c2分别表示上面两者的通行能力；α1、β1、α2、β2为回归系数。

2　原始蚁群和粒子群算法模型

2.1原始蚁群Ant-quantity算法模型

蚁群算法(Ant Colony Optimization, ACO)是一种模拟进化算法[4-5]，该算法具有较强的鲁棒性、正反馈、并行性和分布式协作等优点，但其搜索时间长、易陷入局部解优先和搜索停滞等问题。

当前描述蚁群算法有诸多代表模型，在此选取Ant-quantity模型为改进对象，具体如下

(2)

其中，Lij为ij路段长度；Q为非负常量，表示该路段残留的信息素浓度。

蚂蚁k将n个节点全部遍历结束之后，需要对ij路段的信息素进行局部更新

(3)

其中，ρ和τ0分别表示路段信息素挥发系数和路段信息素初值，其中τ0一般设为0。若数量为m的蚂蚁全部遍历完所有节点时，对于ij路段信息素累加值如下

(4)

与此同时，可得到m个路线解，在此需挑出所有路线解中距离最短的解，并将该路线解进行如下的信息素全局更新

τij(t+n)=(1-ρ)τij(t)+ρΔτij(t)

(5)

2.2标准粒子群算法数学模型

粒子群算法[6-7](Particle Swarm Optimization, PSO)，虽目前粒子群算法在不同改进后性能有所提升，但仍有如控制参数选择、过早收敛等缺陷。以下以标准粒子群算法为改进对象

(6)

(7)

式(6)和式(7)中，ω的不同取值对算法性能影响与Vmax相似。目前惯性权值多采用线性递减权值策略

ω(t)=(ωs-ωe)(Tmax-t)/Tmax+ωe

(8)

3　混合蚁群算法及其改进

针对以上缺点，引入一种融合的智能优化粒子群算法，并对两个算法进行优化融合。在路径搜索初期采用粒子群算法进行粗搜索，并适当增加粗搜索过程中最优路径上的初始信息素浓度，后期则使用蚁群算法进行细搜索，组合改进后的融合算法。

3.1蚁群算法改进

针对蚁群算法出现搜索时间长、易陷入局部解优先和搜索停滞等问题，从限制信息素浓度、启发函数、信息素全局更新规则3方面进行改进，以最大程度提高求解效率。蚁群搜索出的解路线可能不是全局最优解，而是局部最优解。在此引入最大最小信息素[8-9]，该思想和粒子群算法中对粒子速度加以限制，通过这种方法可适当分散各路段信息素分布，从而使蚁群扩大路径搜索，增加最优解的全局性，有效避免了局部最优解和算法搜索停滞的发生。

在实际路线中最优解随着算法迭代数增加而更加优化，应考虑在不同迭代情况下对后续蚂蚁路段选择倾向的不同影响程度，而非原先蚁群算法中启发函数一般只以1/Lij这样和距离有关的静态值。具体如下

(9)

其中，ηij(g)和g2max分别表示算法第g次迭代时的启发函数和算法迭代极值；Lbest(g)和μ分别表示算法前g-1次迭代时的最佳距离解和算法迭代指导因子。

路段信息素初值已不是0或统一值，而是因前期搜索影响形成具有一定差异性的初值，避免蚂蚁对一些极差解路线的探索。改进如下

(10)

式(10)对前期粒子群搜索的最佳路线各路段信息素初值均增加Δτpso，而对于其他路段的信息素初值不做任何修改。以避免数量有限的蚁群资源在较差路段上进行探索搜索，进而提高算法搜索效率。具体改进规则如下

τij(t+n)=

(11)

从式(11)可看出，每次迭代后对处于最差路线且信息素增量最少路段的信息素抑制为Δτij(t)，而其他路段均比其高出(1-ρ)τij(t)。

3.2粒子群算法改进

为实现对粒子飞行速度的控制和调节，标准PSO引入了惯性权重ω，该权值策略为线性递减的。但算法在应用中通常均是非线性且高度复杂的，这一矛盾说明了这种惯性权重与实际情况不符[10-11]。粒子群算法凹函数不仅不会降低算法收敛精度，且能较大幅度提高算法收敛速度。将权值策略改进为如下形式

(12)

其中，ωs和ωe分别表示初始和终止迭代惯性权值，在收敛速度和求解精度平衡点上一般取值0.95和0.4；g和g1max分别表示算法当前迭代数和粒子群算法的迭代极值。

4　算法仿真分析

为检验改进混合算法搜索路线的性能，在Visual Studio应用程序下，将城市道路网抽象模拟成基于点线图论的方式，其中点表示道路交叉口，线表示道路路段。对城市局部路网模型说明：首先，对于道路网数据，按道路等级分为4级，1级道路如节点4～11，2级道路如节点10～11，3级道路如节点3～4，4级道路如节点2～9。路段的距离和车流量分别标示在两节点之间，如1～2路段上的8.9和410。道路网中某些节点设有收费站点，如节点9。如图1所示，程序选择节点1作为起始节点，节点49作为终止节点，程序仿真结果如图1和图2所示。

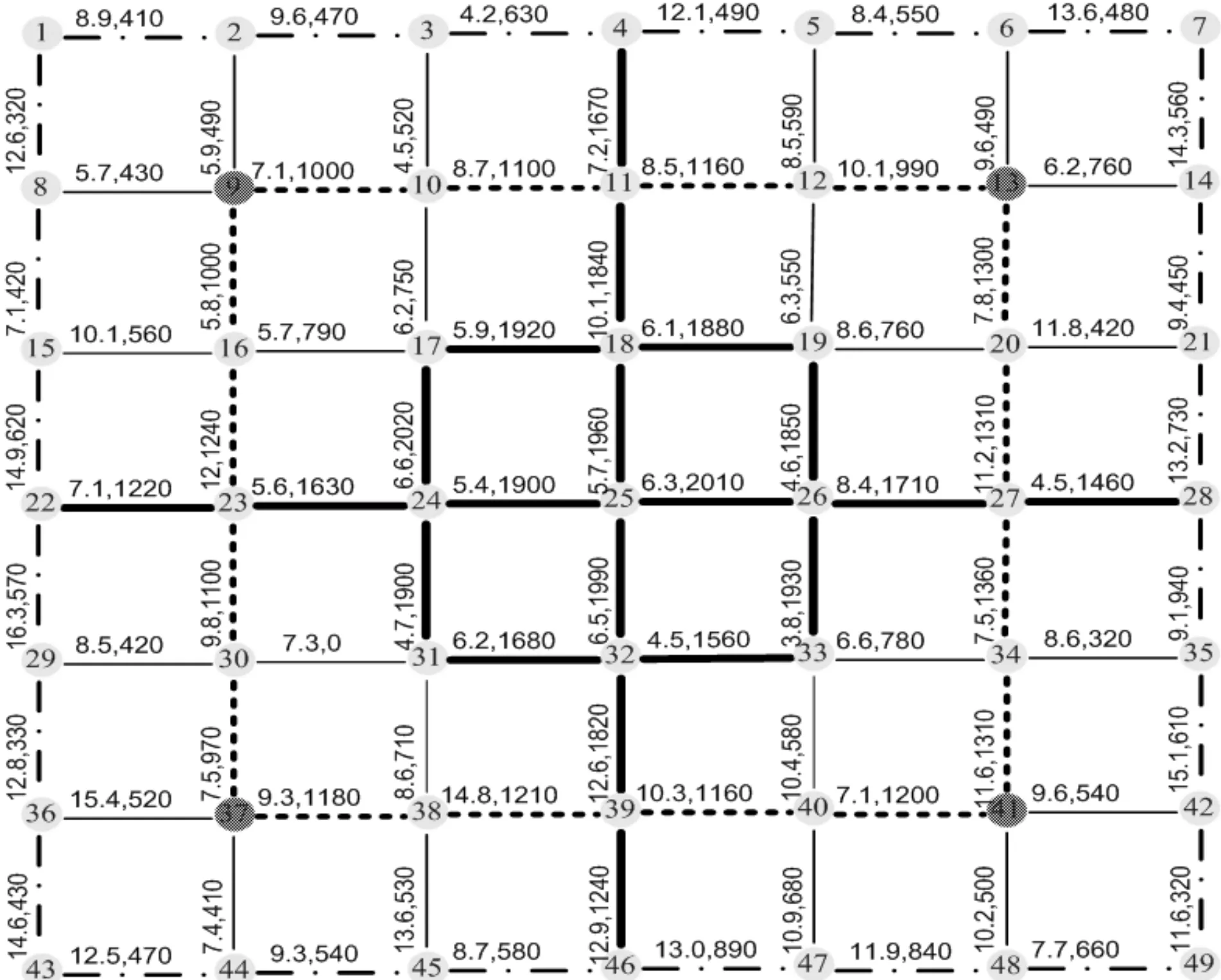
图1　城市局部路网模型

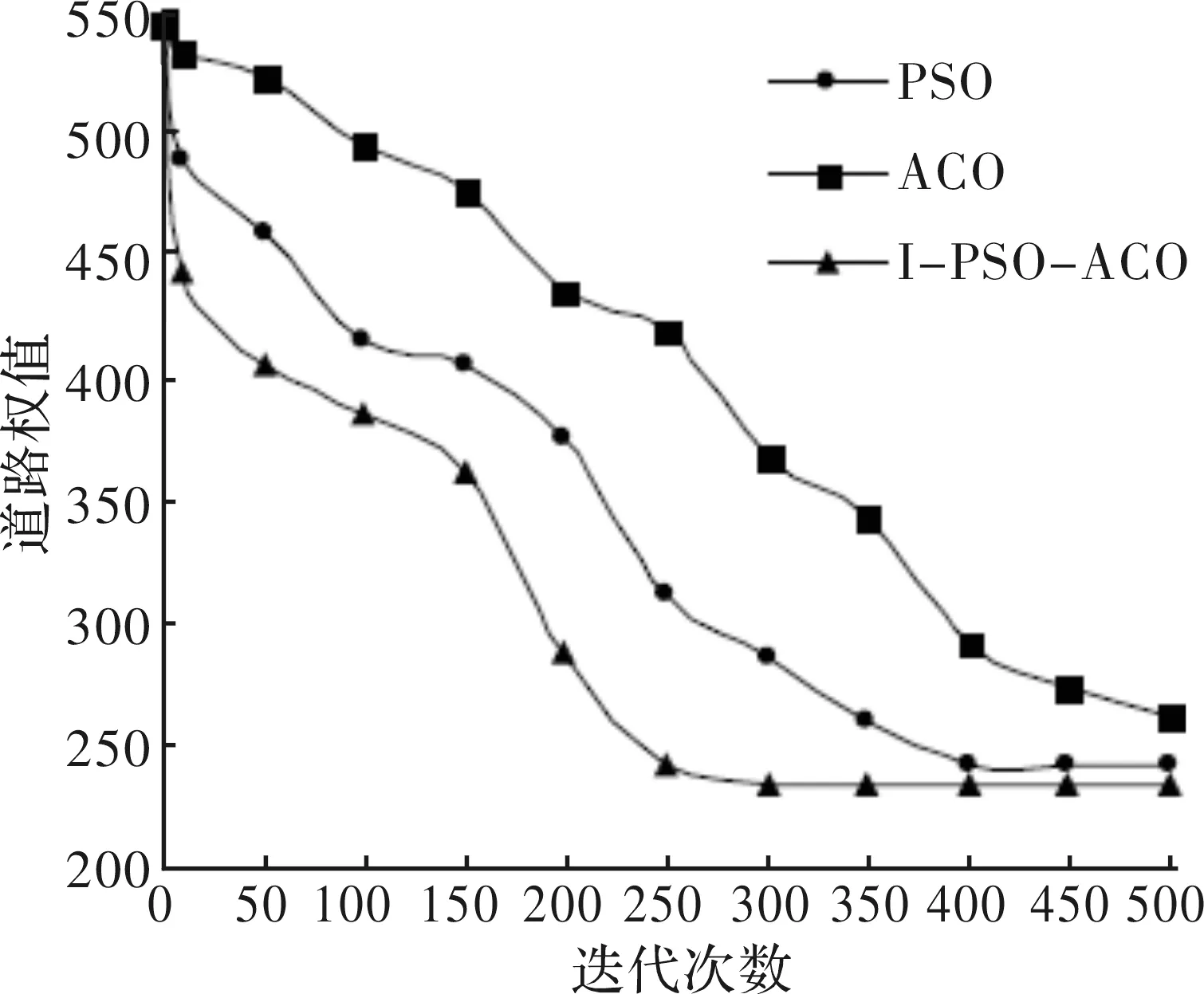
图2　算法收敛与求解曲线图

通过分析仿真结果可知，采用蚁群算法和粒子群算法求得的最佳路线总权值分别为242.4和261.0，而融合算法为233.2。此外，融合算法在迭代150次后开始迅速收敛，并在250次后解趋于稳定。从仿真曲线可知，融合算法在路线规划质量和求解效率上均略优于蚁群和粒子群算法。

为进一步检验混合蚁群算法在最优路径搜索时求解的质量，本文通过安装在另一台计算机中自带Network Analyst功能的ArcMap应用程序，实现路径搜索，如图3所示。

图3　ArcMap正常路况的路径规划

如图3所示，在对环路进行路径规划时ArcMap只为追求权值最小的线路，总距离为0.61 km，时间为0.915 min。

5　结束语

文中通过建立动态路阻权值模型，对现实道路网络用数学模型进行抽象化表达，再分析蚁群算法和粒子群算法各自特点，将两个算法进行融合，形成融合型算法。并根据路径搜索问题对蚁群算法和粒子群算法进行针对性改进，采用图论实验对改进后的混合算法进行仿真，证明新算法在求解准确度和效率上均略有提升。

[1]Halim Ceylan,Michael G H Bell.Traffic signal timing optimisation based on genetic algorithm approach, including drivers’routing [J].Transportation Research,2004,38(4):71-76.

[2]袁振洲.动态交通分配中道路阻抗模型的研究[J].中国公路学报,2002,15(3):92-95.

[3]田璠.基于道路拥挤收费的出行时间价值研究[D].大连:大连理工大学,2009.

[4]张银玲,牛小梅.蚁群算法在移动机器人路径规划中的仿真研究[J].计算机仿真,2011,28(6):231-234.

[5]王胥鹏,胡劲松.一种改进的微粒群算法[J].计算机应用研究,2009,26(10):3642-3645.

[6]曾明如,徐小勇,刘亮,等.改进的势场蚁群算法的移动机器人路径规划[J].计算机工程与应用,2015,51(22):33-37.

[7]柳长安,鄢小虎,刘春阳,等.基于改进蚁群算法的移动机器人动态路径规划方法[J].电子学报,2011,39(5):1220-1224.

[8]王越,叶秋冬.蚁群算法在求解最短路径问题上的改进策略[J].计算机工程与应用,2012,48(13):35-38.

[9]杨帆,胡春平,颜学峰.基于蚁群系统的参数自适应粒子群算法及其应用[J].控制理论与应用,2010,27(11):1479-1488.

[10]那日苏,李强,乌力吉.基于仿生学改进的粒子群算法[J].计算机工程与应用,2014,50(6):61-63.

[11]何少佳,刘子扬.基于惯性蚁群算法的机器人路径规划[J].计算机工程与应用,2012,48(15):245-248.

Application of Improved Fused ACO and PSO Algorithms in Vehicle Routing Search

DU Bo, XIA Chunlei, DAI Shuguang

(School of Optical-electrical and Computer Engineering, University of Shanghai for Science and Technology, Shanghai 200093, China)

The ant colony and particle swarm optimization have the disadvantages of local preferred solution, stagnation and low convergence speed. A fusion of improved ant colony and particle swarm algorithm is proposed to meet the high quality and efficiency requirements of vehicle routing search., use the coarse search is used in the early stage, and the improved ant colony algorithm for the following fine search. Simulation shows that the improved algorithm significant improves the efficiency of path planning and calculation.

impedance model; fused algorithm; path search; simulated analysis

2015- 12- 20

国家自然科学基金资助项目(61170277)；上海市教委科研创新重点基金资助项目(12zz137)；上海市一流学科建设基金资助项目(S1201YLXK)

杜博(1990-)，男，硕士研究生。研究方向：汽车电子。夏春蕾(1974-)，女，讲师。研究方向：信号与信息处理。戴曙光(1957-)，男，教授。研究方向：信息处理，测试计量技术。

10.16180/j.cnki.issn1007-7820.2016.09.002

TP273

A

1007-7820(2016)09-004-04