WSN中基于线性回归和最大似然的缺失值估计模型

陈园园，袁焕丽

(周口师范学院 物理与电信工程学院，河南 周口 466001)



WSN中基于线性回归和最大似然的缺失值估计模型

陈园园，袁焕丽

(周口师范学院 物理与电信工程学院，河南 周口 466001)

为了解决无线传感器网络中感知数据缺失问题，笔者结合基于时间相关性的多元线性回归模型和最大似然估计模型的两种参数估计算法，提出了一种新的缺失值估计算法．该算法不仅可以准确地估算出某时刻缺失对象的信息，而且在时间序列不满足线性模型的情况下仍可以对缺失值进行估计，实验表明该算法有很好的可靠性和稳定性．

无线传感器网络；缺失值估计；线性回归模型；EM算法

无线传感器网络(WSN)早已被列为十大改变未来世界的新兴技术之首[1]．但由于无线传感器网络中节点的通信能力有限，同时又受到高山、河流等地势的影响[2]，部分节点可能监测不到信息或脱离网络，导致这些节点的感知数据信息无法正常传送给汇聚节点，客户终端也无法得到应有的信息．传感器节点的能量有限，当传感器节点不稳定的时候也会采集到异常的数据信息，这些信息无法正常回馈给客户端．当节点能量耗尽时，也会丢失监测数据．另外，传感器节点的存储能力有限，当感知数据量超过缓冲存储器的容量阀值时，同样会造成数据丢失．WSN节点的体积小、构造简单、易损坏，采集的感知数据受到周围环境影响时容易缺损．所以，难免在WSN中出现感知数据缺损的现象．

在采集的过程中，感知数据的缺损严重影响了信息的可用性和利用率，不仅降低了工作效果，而且很可能带来严重的后果．若不对这些缺损的数据集进行有效的处理，研究工作和应用将无法正常进行，若仅对部分缺损数据单元作删除处理，将丢失大量的原始监测数据信息，更会造成网络资源的浪费．因此解决无线网络中数据缺损是许多研究者面临的难题．综上所述，WSN中对缺损数据处理的研究有着重要现实意义和应用前景．

WSN中的感知数据是连续变量，对连续变量的缺失机制的处理方法有EM法、回归法、成组删除法、均值法、MI填充法[3]．对于二分类变量有成组删除法和MI/Logistic回归法对缺失值进行处理．Gruenwald L[4]利用数据挖掘技术提出了一种WARM算法，该算法用相关联的节点数据来估计缺失的数据，主要是针对离散数据进行的处理，而不是连续变化的感知数据．Li等[5]为了实现最少数据以建立数据估计模型的目的，牺牲了对缺失值估计的精度．潘立强等[6-7]采用多元回归模型，提出了一种基于时空相关性的缺失值估计算法．何丽娟等[8]基于Hermite和DESM模型提出了一种基于时空相关性的HD算法，该算法能够自适应的调整估计方程中的权值参数．焉晓贞等[9]提出了基于多变量主元素分析(multiple variable principal Component analysis, MVPCA ) 的不确定性传感数据预测方法，该方法通过MVPCA的特征提取这一预处理手段获得不确定性传感数据的本质特征，然后采用基于相关分析的多元回归方法对这些数据进行建模和预测．目前虽然有许多缺失值估计算法，但在WSN中应用的较少．因此笔者设计了一种新的估计算法，该算法使EM算法和多元线性回归法相结合，可以在缺失率符合WSN数据特点的情况下实现很好的估计效果．

1　模型介绍

1.1最大似然估计模型

EM算法是一种改进的求参数的极大似然估计的方法，该算法在概率模型中寻找参数最大似然估计，可以广泛应用于各种环境下的不完全数据．

EM算法的基本思想是：首先对隐藏变量赋初值，计算其最大似然估计值(E步)；再最大化在 E 步上求得的最大似然值，计算参数的值(M步)．在M 步中得到的参数估计值被用于下一个 E 步计算中，这两个过程循环交替进行，直到最后一个参数估计值和上一个参数估计值相等，停止迭代[10]．E步先估计出期望值，M步是在插补的基础上重新估计，改进系数的最大似然估计．混合模型的估计结果比线性模型下的估计结果更接近真实值，且在缺失率小于30%时，估计结果最理想．

1.2多元线性回归模型的建立

在一个监测区域内每个节点上的大量监测数据都有时间上的相关性，若某一时刻的感知数据缺失，可以基于多元线性回归模型[11]利用相邻时刻的感知数据来估计缺失值．

假设某一节点在ti时刻的感知数据缺失，且在这一时刻有m个相邻时刻的感知数据是已知的，这些时刻分别记作t1,t2,…,tm．采用多元线性回归模型刻画节点在ti时刻的感知数据缺失值，公式如下：

yti=β0+β1yt1+β2yt2+…+βmytm+μi

(1)

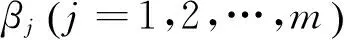
定义：随机误差项μi服从均值为0，方差为σ2的高斯分布，即μi～N(0,σ2)βj.

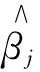
(2)

2　基于回归模型和EM算法的缺失值估计

模型设计

由于WSN节点的监测通常是连续的，即有时间上的相关性，本文采用基于极大似然估计的EM参数估计算法和多元线性回归模型，设计了一种新的TEM算法对缺失值进行估计．该算法首先对数据集进行多元回归建模，用EM算法对系数矩阵进行最大似然估计，然后把估计值作为观测值再进行期望最大化，最后直到收敛结束迭代，把系数矩阵代入多元回归模型中，最终求得缺失值．该算法在缺失率符合WSN数据特点的情况下有很好的估计效果．

当采集的感知数据缺失或坏损时，基于时间相关性，可以利用多元线性回归模型对其进行估计．主要步骤是对相关系数的估计，利用回归模型求得最终估计值．一般的相关系数估计算法采用普通的最小二乘法，这种方法容易发生偏离，而且实际数据的随机性大，并不一定每个数据都满足线性关系，采集的数据也可能存在噪声，使得估计效果不准确．为此采用EM参数估计算法，利用该算法基于最大似然估计模型对相关系数进行估计，EM算法主要用于求后验分布的众数，其主要思想是：首先假定参数值来估计缺失值，然后用这些估计值来更新参数值，反复迭代直到参数值不再发生变化．

问题定义：

假定要预测(xn+1,xn+2,…,xn+m)下的(yn+1,yn+2,…,yn+m)的值．

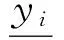
令Y=(Yobs,Ymis)．其中Yobs是已知的感知数据部分(y1,y2,…,yn)， Ymis是缺失数据即待估计的数据部分(yn+1,…,yn+k)，与之对应的X=(Xobs,Xmis)=(x1,x2,…,xn+k)．

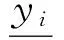
感知数据集Y的分布可以表示为Y=Xβ+ε,ε～Nn(0,σ2In)，所以Y～Nn(Xβ,σ2In)．

可得：

f(Y|β)=

(3)

对数似然函数为：

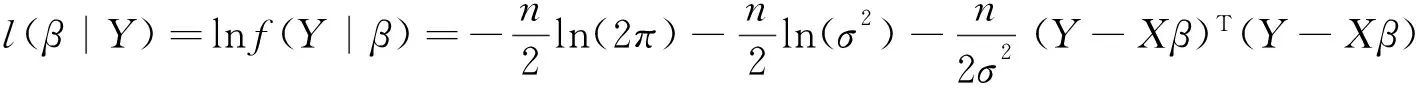
(4)

在上式中仅最后一项含有β，所以似然函数可以简化为：

(5)

EM算法模型的迭代：

E步：对关于Z的条件分布求期望．

(6)

M步：将Q(β|β(i),Yobs)极大化，即找到一个β(i+1)使得

(7)

对上式求导，得

(8)

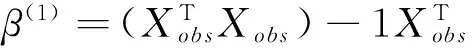
3　仿真实验与结果分析

3.1实验环境及数据

本文针对缺失值估计模型算法进行仿真，开发工具为C++，采用Inter酷睿i5双核处理器，CPU 2.0 GHz，2.0 GB DDR3内存．实验数据采用两个数据集，分别是英特尔伯克利实验室采集的各属性监测值和韩伯电子开发的ZigbeX无线传感器采集的真实数据集．

图1所示为模型的运行结果图，分别显示了数据源部分和参数显示区，数据源可以包括像温度、噪声和频率等属性的数据，参数显示区则显示了在模型迭代过程中每一步计算出的均值和方差，最终由EM模型估计出缺失数据．

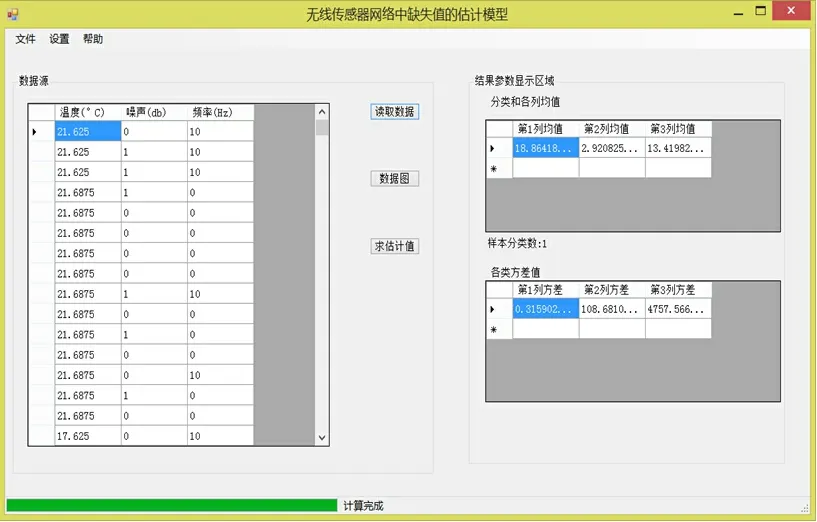
图1　运行结果图

3.2TEM算法仿真结果与分析

为了测试本文中设计的缺失值估计模型的准确性，在完备数据集中，先剔除部分观测值，用算法对感知数据集中的完备数据进行估计，并用估计出来的值与原真实值进行对比．

图2和图3中给出了温度传感器在一段时间内的室内温度实际监测值，同时分别给出了多元线性回归模型的估计结果和TEM模型的估计结果．可以看出多元线性回归的估计值与实际值有很多偏差，而本文中的TEM算法偏差不大，临近的取值也非常接近实际值．

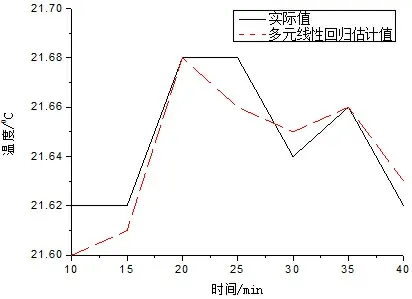
图2　多元线性回归模型室内温度数据估计结果分析图

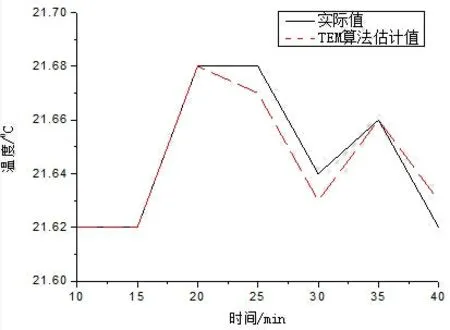
图3　TEM算法室内温度数据估计结果分析图

图4和图5中给出了温度传感器在一段时间内的室外温度实际监测值，同时分别给出了多元线性回归模型的估计结果和TEM模型的估计结果．可以看出多元线性回归的估计值与实际值有较大偏差，而本文中的TEM算法的偏差很小，取得了很好的估计效果．

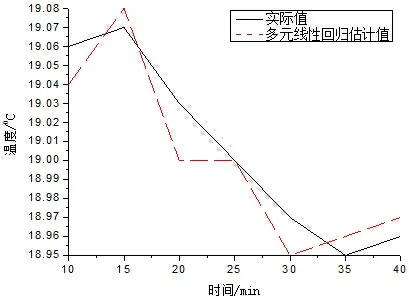
图4　多元线性回归模型室外温度数据估计结果分析图

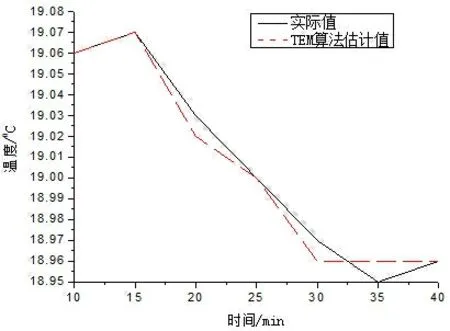
图5　TEM算法室外温度数据估计结果分析图

4　结论

针对WSN中数据缺失的问题，本文介绍了一种基于最大似然估计的EM算法和基于时间相关性的多元回归模型，结合两种模型提出了一种新的WSN中缺失值估计算法.与原来的多元回归模型进行比较，TEM算法有很好的估计效果．

[1] 司海飞，杨忠，王珺．无线传感器网络研究现状与应用[J]. 机电工程, 2011，28(1)：16-20，37.

[2] 苏叶健. 无线传感网技术综述[J]. 信息通信, 2012(6): 275.

[3] 花琳琳. 不同缺失值处理技术的模拟比较[D]. 郑州: 郑州大学, 2012.

[4] Halatchev M, Gruenwald L.Estimating missing values in related sensor data streams[A]. Proceedings of the 11thInternational Conference on Management of Data. Hyderabad, 2005:83-94.

[5] Li Ying-shu, Ai Chun-yu, Deshmukh W P, et al.Data estimation in sensor networks using physical and statistical methodologies[A]. Proceedings of the 28thIEEE International Conference on Distributed Computing Systems. Beijing, 2008:538-545.

[6] 潘立强, 李建中, 骆吉洲.传感器网络中一种基于时空相关性的缺失值估计算法[J]. 计算机学报, 2010, 33(1): 1-11.

[7] 潘立强, 李建中.传感器网络中一种基于多元线性回归模型的缺失值估计算法[J]. 计算机研究与发展, 2009, 46(12): 2101-2110.

[8] 何丽娟, 周鸣争, 陶皖, 等. WSN中不确定数据的估计算法[J]. 计算机工程与应用, 2011, 47(28): 100-102.

[9]焉晓贞, 谢红, 王桐.WSN的不确定传感数据预测[J]. 应用科学学报, 2012, 30(6): 567-572.

[10] Ephraim Y, William J. An EM algorithm for markov modulated markov processes[J]. IEEE Transactions on Signal Processing, 2009, 57(2): 463-470.

[11] 李庆阳, 王能超, 易大义. 数值分析[M]. 北京: 清华大学出版社, 2008: 25-28.

A missing value estimation model based on linear regression and maximum likelihood for WSN

CHEN Yuanyuan , YUAN Huanli

(School of Physics and Telecomunication Engineering,Zhoukou Normal University, Zhoukou 466001,China)

In order to solve the wireless sensor networks perceived problem of missing data, the author parameter estimation algorithm based on two temporal correlation of multiple linear regression model and maximum likelihood estimation model, we propose a new estimation of missing values. The algorithm not only can accurately estimate the time of a lack of information about the object, and in the case of time series does not satisfy the linear model is still able to estimate missing values, experiments show that the algorithm has good reliability and stability.

wireless sensor network; missing value estimation; linear regression model; EM algorithm

2016-03-17;

2016-04-20

河南省高等学校重点科研项目(No.16B510009)；河南省科技厅科技攻关项目(No.162102310607)；河南省教育厅项目(No.2016-JSJYYB-096)

陈园园(1986-)，女，河南周口人，硕士，主要研究方向：通信和信息处理．

TP393

A

1671-9476(2016)05-0071-04

10.13450/j.cnki.jzknu.2016.05.018