垂直于正交异性与各向同性双材料界面裂纹尖端应力场理论研究
2016-10-17胡帅帅
胡帅帅,陈 娜
(周口师范学院 数学与统计学院,河南 周口 466001)
垂直于正交异性与各向同性双材料界面裂纹尖端应力场理论研究
胡帅帅,陈娜
(周口师范学院 数学与统计学院,河南 周口 466001)
主要研究了各向同性与正交异性材料中与材料界面垂直的裂纹尖端问题.通过傅里叶积分变换推导出了裂纹尖端的位移、应力场表达形式.构造位错密度函数并结合相应的边界条件,将问题转化为奇异积分方程.最后给出应力强度因子的表达式并分析了对其影响的相关因素.
各向同性材料;正交异性材料;垂直裂纹;傅里叶变换;应力强度因子
随着复合材料在工程领域中应用的不断扩大,复合材料中各种各样的裂纹尖端研究就显得非常重要.文献[1]采用梅林变换法研究一类垂直裂纹问题.文献[2]用liyong-mellin变换方法研究的是各向同性双材料垂直裂纹问题.文献[3]、[4]、[5]利用积分变换方法研究的是裂纹垂直于一非理想界面的问题.文献[6]采用复变函数方法讨论了正交各向异性双材料界面裂纹.
本文通过傅里叶积分变换推出了正交异性与各向同性垂直界面裂纹尖端位移、应力场的表达形式,结合相应的边界条件将问题化成第一类奇异积分方程,得出了应力强度因子的表达式并分析了对其影响的相关因素.

图1 含有垂直于各向同性、正交各向异性双材料界面裂纹
1 力学模型
如图1:y轴为双材料结合面,长度为2a0的裂纹位于各向同性材料中且垂直于双材料界面,裂纹中心距界面距离为c.裂纹被置于x轴上并完全含于各向同性材料. 在材料内部给垂直裂纹施加一压力,即
(1)
2 基本方程
由弹性力学知识可知,各向同性、正交各向异性材料的控制方程可表示为:
(2a)
(2b)
(2c)
(2d)
物理方程:
(3a)
(3b)
(3c)
(3d)
(3e)
(3f)
根据弹性力学知识构造如下边界连续条件:

(4)
v(1)(x,0)=0 ;0 (5) (6) (7) (8) 2.1 模型求解 考虑到问题的对称性,只需考虑右半部分即可,通过傅里叶积分变换构造方程(2a)~(2d)的解为: (9a) (9b) (9c) (9d) 其中 (10) (11) 2.2裂纹尖端应力场 把方程(9a)~(9d)带入方程(3a)~(3f)中可得: (12a) (12b) (12c) (12d) (12e) (12f) 由上式,求出Αj(s)和Βj(s) (j=1,2,3,4)就可以得出裂纹尖端应力场的具体表达式.由边界连续条件(4)~(8)可得: (13) (14) (15) (16) (17) (18) (19) 对方程(18)、(19)进行傅里叶积分逆变换可得: (20) (21) 其中 (22) (23) 由方程(15)、(17)、(20)、(21),未知函数Α3(s)、Α4(s)、Β3(s)、Β4(s)可以用关于ω1,ω2的表达式表示.即 (24) 这里,不再给出Cj(s)、Dj(s)(j=1,2,3,4)的具体表达式. 由边界条件v(1)(x,0)=0, 0 (25) (26) 2.3 求解第一类积分方程方法 方程(26)很难求解,可以把其化成带有柯西核的奇异积分方程,然后通过数值计算得出结果.为此,定义辅助位错密度函数g(x) (27) 可得: (28) 又由于v(1)(a,0)=v(1)(b,0)=0,则位错密度函数g(x)满足单值约束条件. (29) 对方程(28)就行傅里叶积分逆变换,可得: (30) 把方程(30)代入方程(26),则方程可以转化成: (31) 其中 (32) 观察方程(32)知,只有当k(ξ,x)具有较简单的形式时,方程(31)才容易求解.为此引入无量纲变量: (33) 此时方程(31)化为: (34) 这里 (35) 接下来通过切比雪夫配置方法把方程(34)离散成一个线性代数方程组 (36) 这里 λ1=...=λn-1=1 另外单值约束条件可以写为: (37) 求解线性方程组(36)、(37),就可以得到裂纹尖端应力场、位移场. 根据断裂力学的知识,定义裂纹尖端左右端的应力强度因子如下: (38) 由式(35)可得: (39) 当两种复合材料均为各向同性材料时.计算可得: k(ξ,x)=0 此时奇异积分方程(36)可以被表示为: (40) 由式(39)裂纹尖端左右端的应力强度因子为: (41) 与文献[7]结果一致. (1)构造出垂直于正交异性与各向同性双材料界面裂纹的力学模型. (2)通过傅里叶积分变换、逆变换推导出正交异性与各向同性双材料界面裂纹的位移场、应力场,并给出了裂纹端应力强度因子的具体表达式. (3)验证两种材料均为各向同性材料时,推导出的应力强度因子表达式与已知结论一致. [1]Bogy D B.Two edge-bonded elastic wedges of different materials and wedge angles under surface tractions[J].ASME Journal of Applied Mechanics,1971,38:377-386. [2]COOK T S, Erdogan F. Stresses in bonded materials with a crack perpendicular to interface [J]. International Journal of Engineering Science,1972, 10:677-697. [3]Jinquan Xu. Interface Mechanics [M].Beijing:Science Publishing House, 2006. [4]Zhong X C,Li X F,Lee K Y. Analysis of a mode-I crack perpendicular to an imperfect interface[J]. International Journal of Solids and Structures,2009,46:1456-1463. [5]Zhang X S. A central crack at the interface between two different orthotropic media for the mode Ⅰand mode Ⅱ [J]. Engineering Fracture Mechanics, 1989, 33 (3):327-333. [6]李俊林,张少琴,杨维阳,等.正交异性双材料半无限界面裂纹尖端场分析[J].应用力学学报,2010,27(3):444-450. [7]周振功,王彪. 位于两不同正交各向异性半平面间张开型界面裂纹的性能分析[J]. 应用数学和力学, 2004,25(7):887-1000. Analysis of a crack perpendicular to the interface between isotropic and orthotropic composite materials HU Shuaishuai,CHEN Na (School of Mathematics and Statistics, Zhoukou Normal University, Zhoukou 466001,China) The problem of a crack perpendicular to the interface between isotropic and orthotropic composite materials is investigated. By using Fourier integral transform, the displacement and the solution of stress field form crack tip is given. By introducing auxiliary dislocation density function and using the corresponding boundary conditions, the problem is transformed into the first category singular integral equation. Finally, the expressions of stress intensity factor are given and the relevant factors which influence the stress intensity factor are analyzed. orthotropic materials; isotropic materials; Mode I perpendicular crack; Fourier transform; stress intensity factor 2016-05-18; 2016-06-12 周口师范学院青年科研基金资助项目(No. zknuB315211) 胡帅帅(1986- ),男,河南漯河人,硕士,主要研究方向为微分方程理论及应用.E-mail:hsshuai@163.com O174.2;O346.1 A 1671-9476(2016)05-0044-06 10.13450/j.cnki.jzknu.2016.05.011










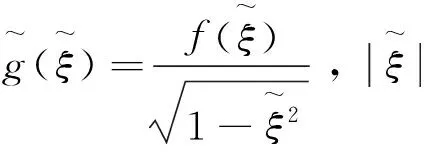
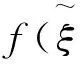


3 应力强度因子
4 结论
