计及受电弓幅频特性的受电弓参数与吊弦间距匹配研究

姜　静， 刘志刚， 鲁小兵， 段甫川， 宋　洋

(西南交通大学 电气工程学院，成都　610031)



计及受电弓幅频特性的受电弓参数与吊弦间距匹配研究

姜静， 刘志刚， 鲁小兵， 段甫川， 宋洋

(西南交通大学 电气工程学院，成都610031)

首先推导了受电弓的稳态幅频特性，结合对接触压力波动原因的分析，得出了受电弓参数与吊弦频率的匹配关系;然后逐一改变受电弓参数，分析受电弓幅频特性，可得受电弓弓头质量和刚度对受电弓幅频特性的影响明显;最后在建立的弓网动态模型中，分别调整受电弓弓头质量和刚度，统计得到接触压力标准差，验证了匹配的效果。研究结果表明，在运行中受电弓通过吊弦间隔的频率若为f，调整受电弓的参数，使受电弓幅频特性在频率f处有极小值，能有效降低接触压力的波动，有利于改善受流。该匹配关系可为弓网系统设计、选型和评价提供参考。

接触网；受电弓；幅频特性；接触压力波动；匹配

电气化铁路受电弓-接触网系统通过不间断的机械和电气接触为列车供电，弓网动态接触成为限制列车速度的一个重要因素[1]。弓网动态接触性能是弓、网各自动态性能相互作用的结果，存在弓网双方的参数是否匹配的问题。因而研究其参数匹配关系具有重要意义。

国内外对改变受电弓、接触网参数对受流的影响做了一定研究，PARK等[2]仅考虑接触网跨距内的弹性变化，用解析的方法分析了受电弓质量、刚度、阻尼等参数对受流质量的敏感性。LEE等[3]用有限元软件SAMCEF建立了弓网耦合模型，在分析受电弓参数敏感性基础上，采用优化方法对参数进行优化。ZHANG等[4]搭建了弓网半实物仿真平台，根据仿真结果研究了接触网预弛度，受电弓阻尼等对受流的影响。

以上弓网参数对受流影响的研究都是基于改变弓或网一方的参数对仿真结果进行比较的思路，没有考虑弓网参数的匹配性对结果的影响。首先建立有效的弓网模型，推导了受电弓的稳态频域特性，并分析了受电弓参数对其特性的影响；接着对仿真数据进行处理，分析了接触压力的变化特征；最后，引出匹配关系：调整弓头质量和刚度使受电弓幅频特性的极小值与吊弦间距相匹配，可以降低接触压力的标准差，有利于改善受流，并在仿真中对该匹配关系进行了验证。

1　弓网系统建模

考虑到受电弓复杂的铰链结构，与接触网的非线性等原因，难以用解析的方法准确的模拟弓网动态接触过程。目前，在研究弓网动态问题的文献中，广泛采用数值方法[5-7]。本文将接触网用带张力的欧拉梁代替[8]，受电弓简化为3自由度集中质量模型[9]，该模型可以有效模拟真实受电弓0～20 Hz的振动[10]，使用罚函数法[11-14]模拟弓网之间的接触过程。

图1为接触网的一个微分段，对其进行受力分析得到其运动微分方程为：

(1)

式中：y(x,t)为振动产生的垂向位移；ρ为微分段线密度；EI为微分段抗弯刚度；Fc(x,t)为受电弓抬升力；Q、M、S分别为接触线截面的剪切应力、弯矩和拉力；φ为张力与水平面夹角。

图1　接触网微分段受力分析Fig.1　The force analysis of the micro-segmentation of the catenary

利用分离变量法对式(1)求解可得到接触网的振动微分方程：

(2)

(3)

式(2)为承力索运动微分方程，式(3)为接触线运动微分方程。

式中:Fa1(x,t)和Fa2(x,t)分别为吊弦和支撑杆对承力索的作用力;Fb1(x,t)和Fb2(x,t)为吊弦和定位器对接触线的作用力;p为吊弦个数;q支撑杆或者定位器个数;ωan和ωbn分别为承力索和接触线自振角频率;qan和qbn分别为承力索和接触线的各阶幅值。

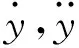
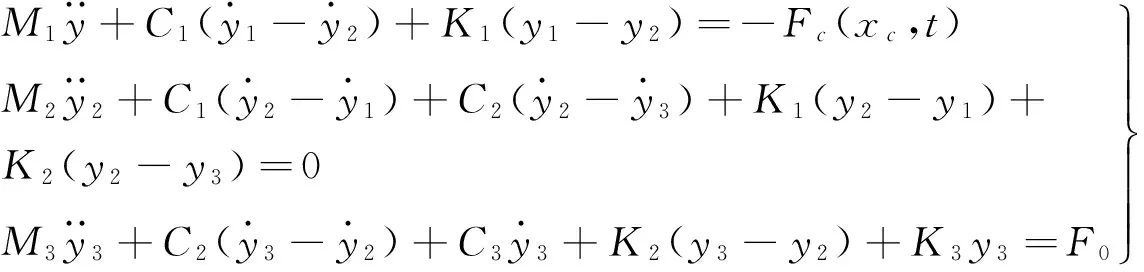
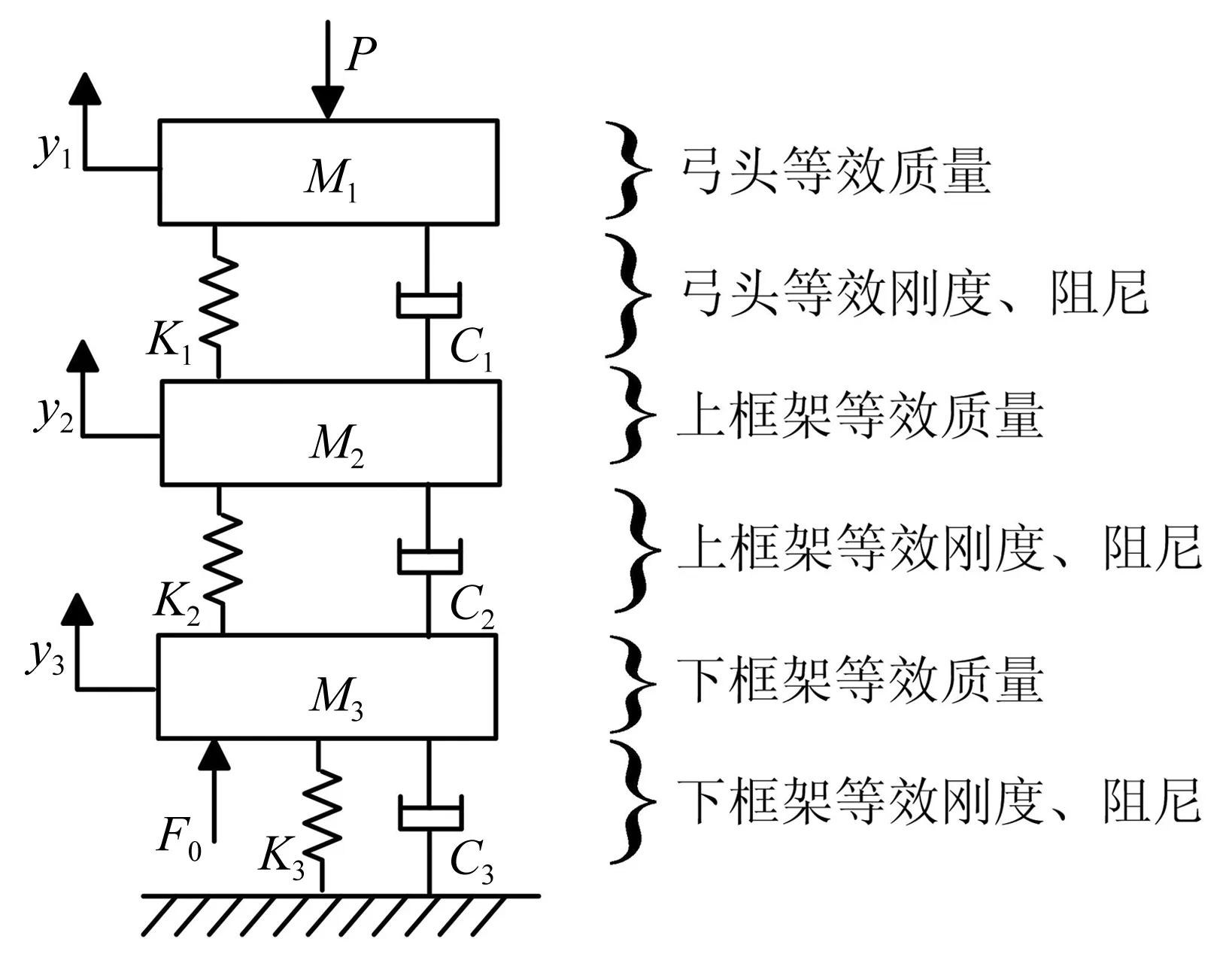
图2　受电弓模型Fig.2　The model of the pantograph

采用罚函数法进行弓网耦合，设接触刚度为Ks，则接触压力为：

(5)

2　接触压力波动分析

2.1接触压力波动的原因

由于受电弓的激励等原因产生的机械波在接触网中传播，在支柱和吊弦等固定约束和集中质量点，机械波将产生反射，反射波与运行的受电弓相遇会使弓网接触压力发生变化[15]，机械波在接触网中的传播(见图3)。在受电弓运行过程中，反复受到支柱和吊弦引起的反射波作用，弓网接触压力因而呈现出周期性变化特征。接触压力变化幅度与反射波频率、幅值，弓的运行速度，弓和网机械阻抗等有关[16-19]。具体的影响关系如式(6)：

(6)

式中:Fp为接触压力变化幅值;β为车速与接触线波动速度比值;ω和A分别为反射波频率和幅值;Zt和Zp分别为接触线和受电弓机械阻抗。

根据式(6)的关系，若其他变量保持不变，减小受电弓机械阻抗Zp能降低接触压力的变化幅值。

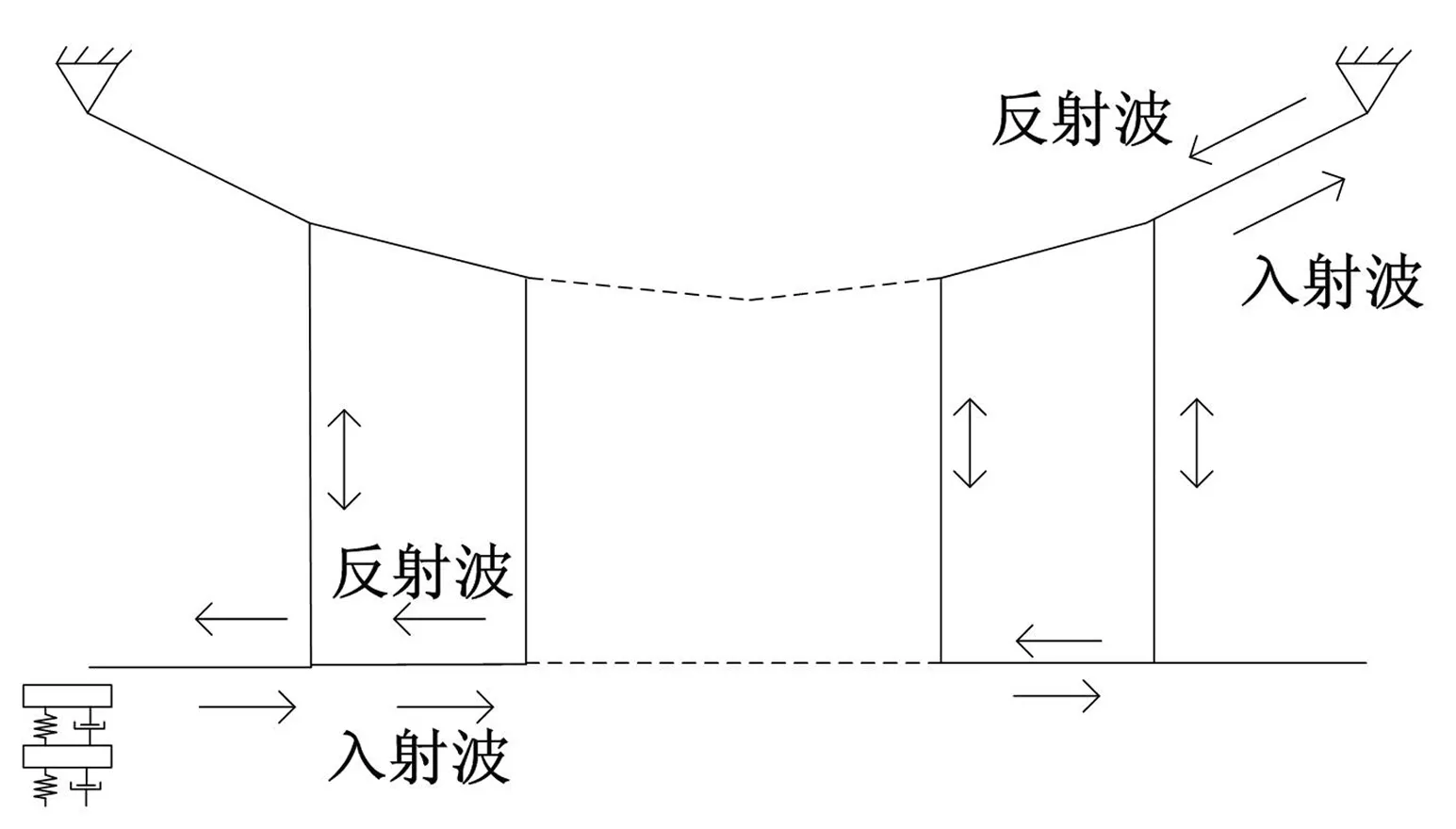
图3　接触网中的机械波传播Fig.3　The incident wave motion of the catenary

2.2受电弓的稳态频域分析

(7)

式中：

A(s)=M1M2M3s6+M1M2C3s5+(M1M2K2+

M1M2K3+M1M3K1+M1M3K2+M2M3K1)s4+

(M1C3K1+M1C3K2)s3+(M1K1K2+M1K1K3+M1K2K3+

M2K1K2+M2K1K3+M3K1K2)s2+C3K1K2s+K1K2K3

B(s)=[M2M3s4+M2C3s3+(M2K2+M2K3+M3K1+

M3K2)s2+(C3K1+C3K2)s+(K2K3+K1K2+K1K3)]s

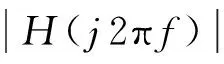
图4　受电弓机械阻抗Fig.4　The impedance of the pantograph

假设接触网吊弦间距为d，若受电弓运行速度为v，则可定义接触线吊弦频率=v/d。通过接触压力波动原因分析，可以到见图5的匹配关系，图5中实线曲线表示未改变受电弓参数时的幅频特性，虚线曲线表示改变参数厚的幅频特性。改变参数，使受电弓幅频特性极小值对应的频率fz2右移以逐渐与吊弦频率吻合，将会有效降低受电弓在吊弦频率处的机械阻抗，减小反射波在吊弦处对接触压力的影响，从而使接触压力更趋近平滑。接触压力趋近平滑，降低弓网接触压力的波动将有利于改善受流。

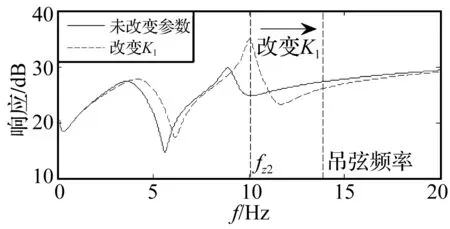
图5　匹配关系示例Fig.5　The sample of the coupling relationship

上述关系是受电弓参数和接触网吊弦频率之间的一种匹配关系。下面在仿真中，通过逐渐改变受电弓参数，使受电弓幅频特性曲线的极小值点逐渐靠近并大于吊弦频率，分析接触压力曲线、标准差的变化趋势，对匹配关系进行验证。

3　受电弓参数与吊弦的匹配与仿真验证

3.1受电弓参数幅频特性的影响分析

本文采用DSA250型受电弓进行研究，其参数见表1。

表1　DSA250型受电弓参数

图6(a)～图6(f)分别显示了受电弓的弓头、上框架和下框架的质量与刚度对幅频特性的影响，图中竖直虚线代表吊弦频率。可以发现：

(1) 弓头刚度K1显著影响机械阻抗转折频率fz2的大小，增大K1会使转折频率fz2逐渐接近并超过吊弦频率，而对离转折频率较远处的响应影响较小。

(2) 上框架刚度K2同样显著影响机械阻抗转折频率fz2的大小，但随着fz2逐渐接近并超过吊弦频率，响应也随之增大，即机械阻抗并不会有明显降低。

(3) 下框架刚度K3本身数值较小，且改变其大小对响应基本无影响。

(4) 弓头质量M1对大于转折频率fz2的较高频率响应的影响较大，减小M1，较高频率较宽范围内的响应将会降低，即机械阻抗将减小。

(5) 上框架质量M2对频率响应的影响与K2相似，虽然对频率影响较大，但响应也随之增大，在吊弦频率处机械阻抗变化不大。

(6) 下框架质量M3对较低频响应作用较大，减小M3,fz1与fz2逐渐增大，但fz2处的响应也随之增大，机械阻抗变化不大。

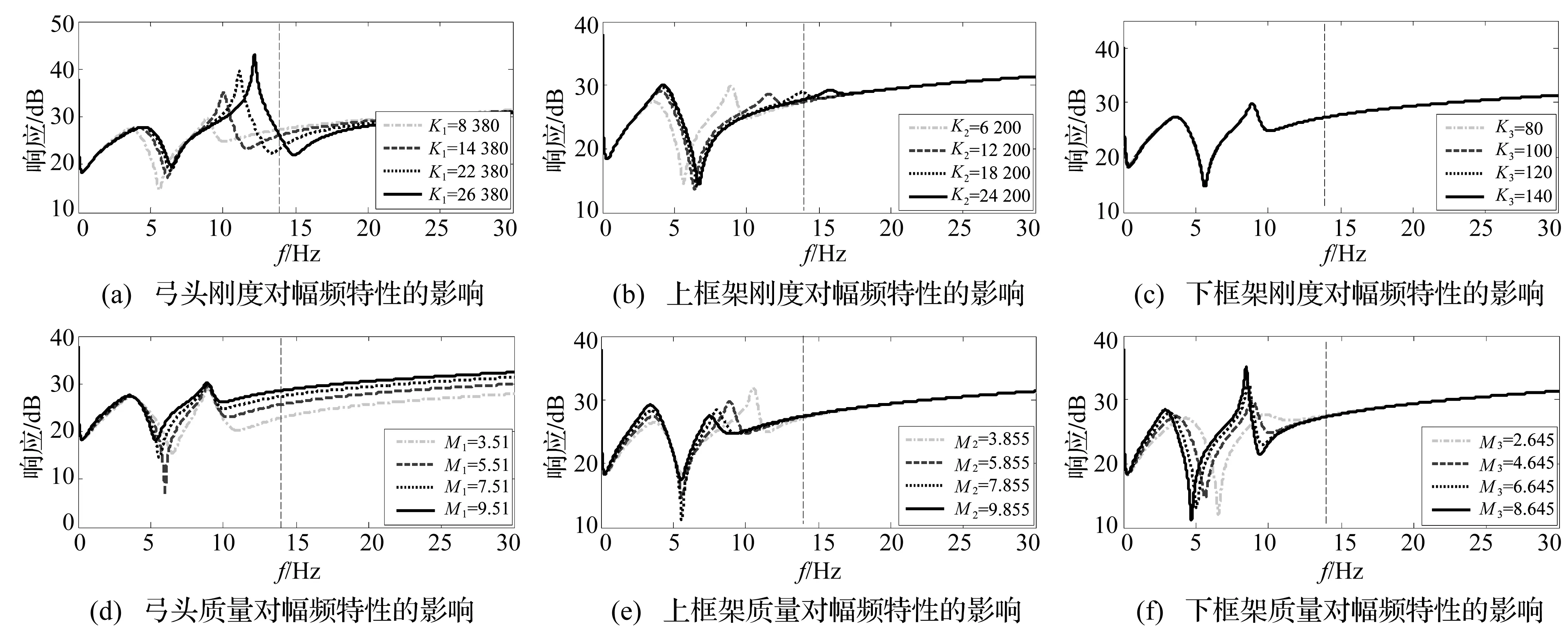
图6　不同受电弓参数变化下的幅频特性对比Fig.6　Comparison of the amplitude-frequency characteristics by changing pantograph parameters individually

通过以上分析，可以看到K1与M1对机械阻抗转折频率fz2影响显著，能有效减小吊弦频率处的机械阻抗，而M2、M3与K2、K3对受电弓在吊弦处机械阻抗影响不大。

3.2仿真验证

以250 km/h情况为例对验证过程进行说明，本例接触网的吊弦间隔为d=5 m，对应的吊弦频率为13.89 Hz。

逐渐增大K1，使K1从原值8 380 N/m逐渐增加到33 380 N/m，图7显示了与K1对应的幅频曲线的变化，图7中随K1增大，转折频率fz2逐渐接近并超过了吊弦频率，其中竖直虚线代表吊弦频率。K1、对应的谐振频率和接触压力标准差列于表2。图8显示了接触压力的标准差随转折频率fz2的变化趋势，可见当fz2与吊弦频率接近时，压力的标准差最小，即接触压力在此时波动程度最低。选取K1=8 380 N/m和K1=23 380 N/m两组接触压力数据，分析对比其接触压力变化曲线，如图9所示，实线曲线(K1=23 380 N/m)所代表的接触压力在大多数吊弦之间的波动幅值有所降低。

图7 K1对幅频特性的影响Fig.7Influenceoftheamplitude-frequencycharacteristicsbyK1图8 改变M1时受电弓谐振频率与压力标准差关系Fig.8TherelationshipbetweenresonancefrequencyandstatisticofthecontactforcewiththechangeofM1图9 改变M1时接触压力变化对比Fig.9ThecomparisonofdifferentcontactforceswiththechangeofM1

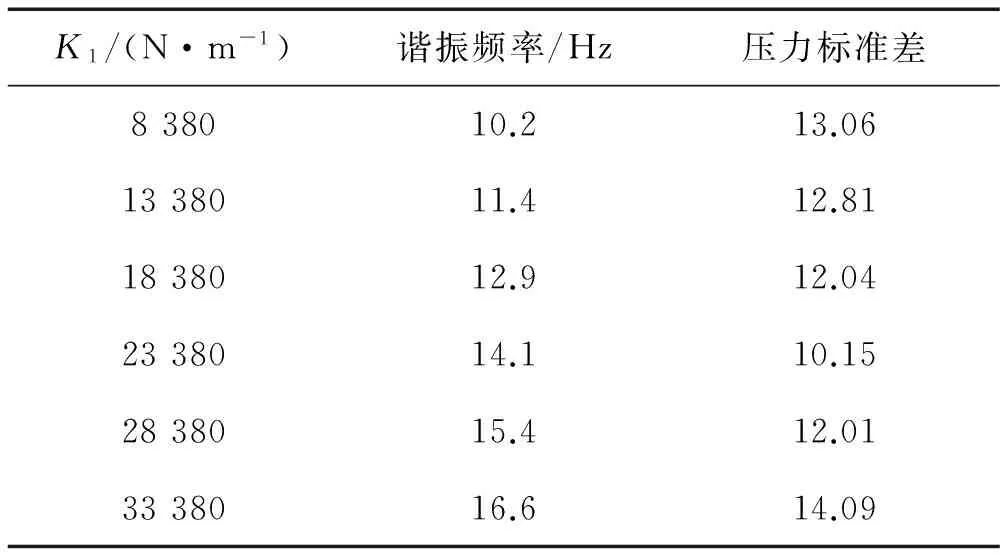
表2　 不同K1值下的谐振频率、压力标准差统计量

逐渐减小M1，使M1从原值7.51 kg逐渐减小到1.51 kg，表3列出了M1与对应的受电弓幅频曲线转折频率fz2和接触压力标准差的值。图10显示了与M1对应的幅频曲线的变化，图10中随M1减小，转折频率fz2逐渐接近吊弦频率，并在M1=1.51 kg时突降等于吊弦频率，其中竖直虚线代表吊弦频率。图11显示了接触压力的标准差随转折频率fz2的变化趋势，当fz2与吊弦频率接近时，压力的标准差最小，即接触压力在此时波动程度最低。选取M1=7.51 kg和M1=1.51 kg两组接触压力数据，分析对比其接触压力变化曲线(见图12)，可见后者接触压力在大多数吊弦之间的波动幅度有所降低，且接触压力在均值附近更加集中。

图10 M1对幅频特性的影响Fig.10Influenceoftheamplitude-frequencycharacteristicsbyM1图11 改变M2时受电弓谐振频率与压力标准差关系Fig.11TherelationshipbetweenresonancefrequencyandstatisticofthecontactforcewiththechangeofM2图12 改变M2时接触压力变化对比Fig.12ThecomparisonofdifferentcontactforceswiththechangeofM2

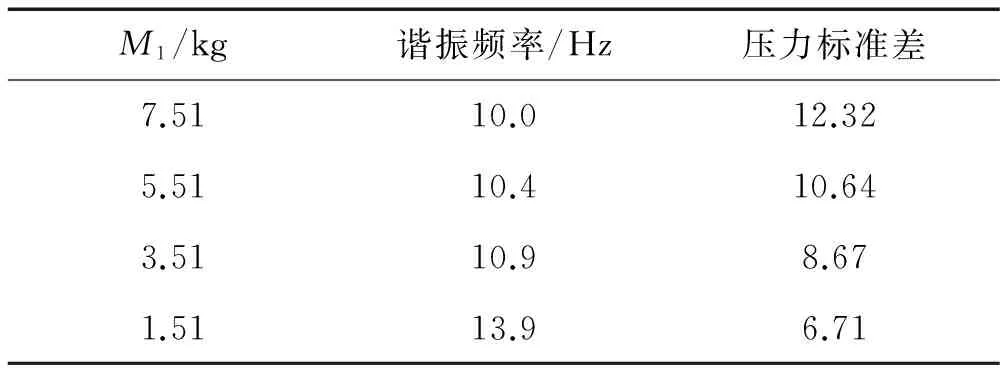
表3　不同M1值下的的谐振频率、压力标准差统计量

通过上述分析对比，验证了结论：调整受电弓参数，使受电弓幅频曲线的转折频率fz2接近受电弓通过吊弦间隔的频率，可以有效降低接触压力在吊弦之间的波动幅度，减小接触压力的标准差，在一定程度上改善受流质量。

4　结　论

首先建立了有效的弓网模型，分析了接触压力变化的原因，结合受电弓机械阻抗的特性，引出并验证了受电弓参数与吊弦间隔的匹配关系。结论总结如下：

(1) 受电弓的机械阻抗整体上随频率的增大而增大，但在转折频率fz1和fz2处有极小值；弓头质量和刚度对转折频率处的响应影响较大。

(2) 调整受电弓弓头质量和刚度，使在接触压力作用下受电弓幅频特性曲线的转折频率fz2与运行中的受电弓通过吊弦的频率相等，可以有效降低接触压力在吊弦之间的波动幅度，减小接触压力的标准差，有利于改善受流质量。

(3) 本文得出的这种匹配关系可以为弓网系统设计、选型提供一个参考方向，从而在需要时依据该匹配关系对受电弓参数或吊弦间距作相应的调整。下一步研究将在本文分析结果基础上，以受电弓结构的相关标准为基础，探讨研究获得实现优化参数的具体实施办法和措施，并进行充分的试验验证。

[1] 于万聚, 高速电气化铁路接触网[M].成都: 西南交通大学出版社, 2003.

[2] PARK T J, HAN C S, JANG J H. Dynamic sensitivity analysis for the pantograph of a high-speed rail vehicle[J]. Journal of Sound and Vibration, 2003, 266(2): 235-260.

[3] LEE J H, KIM Y G, PAIK J S, et al. Performance evaluation and design optimization using differential evolutionary algorithm of the pantograph for the high-speed train[J]. Journal of Mechanical Science and Technology, 2012,26(10): 3253-3260.

[4] ZHANG W H, MEI G M, WU X J, et al. A study on dynamic behavior of pantographs by using hybrid simulation method[J]. Proceedings of the Institution of Mechanical Engineers, Part F: Journal of Rail and Rapid Transit, 2005, 219(3): 189-199.

[5] 汪宏睿, 刘志刚, 宋洋, 等. 高速铁路接触线气动参数仿真及风振响应研究[J]. 振动与冲击, 2015, 34(6): 6-12.

WANG Hongrui, LIU Zhigang, SONG Yang, et al. Aerodynamic parameters simulation and wind-induced vibration responses of contact wire of high-speed railway[J]. Journal of Vibration and Shock, 2015,34(6):6-12.

[6] SONG Y, LIU Z, WANG H, et al. Nonlinear modelling of high-speed catenary based on analytical expressions of cable and truss elements[J]. Vehicle System Dynamics, 2015,53(10): 1-25.

[7] 李敏, 李丰良, 马俊. 高速受电弓的力学模型及运动微分方程[J]. 铁道科学与工程学报, 2005, 2(3): 83-87.

LI Min, LI Fengliang, MA Jun. Mechanical models and differential equations of motion for high speed pantograph[J]. Journal of Railway Science and Engineering, 2005,2(3): 83-87.

[8] 程维. 电气化铁道受电弓-接触网系统受流特性研究[D]. 成都: 西南交通大学, 2004: 6-62.

[9] ZHOU N, ZHANG W. Investigation on dynamic performance and parameter optimization design of pantograph and catenary system[J]. Finite Elements in Analysis and Design,2011,47(3): 288-295.

[10] POETSCH G, EVANS J, MEISINGER R, et al. Pantograph/catenary dynamics and control[J]. Vehicle System Dynamics, 1997, 28(2/3): 159-195.

[11] 李瑞平, 周宁, 吕青松, 等. 横风环境中弓网动力学性能分析[J]. 振动与冲击, 2014, 33(24): 39-44.

LI Ruiping, ZHOU Ning, LÜ Qingsong, et al. Pantograph-catenary dynamic behavior under cross wind[J]. Journal of Vibration and Shock, 2014,33(24):39-44.

[12] 郭京波, 杨绍普, 高国生. 变刚度弓网系统主动控制研究[J]. 振动与冲击, 2005, 24(2): 9-11.

GUO Jingbo, YANG Shaopu, GAO Guosheng. Research on active control of the pantograph-catenary system with varying stiffness[J]. Journal of Vibration and Shock, 2005, 24(2): 9-11.

[13] 李瑞平, 周宁, 张卫华, 等. 高速列车过隧道对弓网动力学影响分析[J]. 振动与冲击, 2013, 32(6): 33-37.

LI Ruiping, ZHOU Ning, ZHANG Weihua, et al. Influence of high-speed trains passing through tunnel on pantograph-catenary dynamic behaviors[J]. Journal of Vibration and Shock, 2013, 32(6):33-37.

[14] POMB J. Multiple pantograph interaction with catenaries in high-speed trains[J]. Journal of Computational and Nonlinear Dynamics, 2012, 7(4):1-7.

[15] KIE β Ling, PUSHCHMANN, SCHMIEDER. 电气化铁道接触网[M]. 中铁电气化局集团有限公司,译. 北京：中国电力出版社，2004.

[16] 宋洋, 刘志刚, 汪宏睿, 等. 接触网三维模型的建立与风偏的非线性求解[J]. 铁道学报, 2015,37(4): 30-38.

SONG Yang, LIU Zhigang, WANG Hongrui, et al. Establishment of 3D model for catenary and nonlinear solution for its wind deflection[J]. Journal of the China Railway Society, 2015, 37(4):30-38.

[17] 宋洋, 刘志刚, 汪宏睿, 等. 脉动风下高速铁路接触网抖振对弓网受流性能的影响[J]. 铁道学报, 2014, 36(6): 27-34.

SONG Yang, LIU Zhigang, WANG Hongrui, et al. Influence of high-speed railway catenary buffeting on pantograph catenary current collection under fluctuating wind[J]. Journal of the China Railway Society, 2014,36(6):27-34.

[18] ABOSHI M, MANABE K. Analyses of contact force fluctuation between catenary and pantograph[J]. Quarterly Report of RTRI, 2000, 41(4): 182-187.

[19] JUNG S P, KIM Y G, PAIK J S, et al. Estimation of dynamic contact force between a pantograph and catenary using the finite element method[J]. Journal of Computational and Nonlinear Dynamics, 2012, 7(4): 041006.

Coupling performance between pantograph parameters and dropper spacing considering the amplitude-frequency characteristics the of pantograph

JIANG Jing, LIU Zhigang, LU Xiaobing, DUAN Fuchuan, SONG Yang

(School of Electrical Engineering, Southwest Jiaotong University, Chengdu 610031, China)

The amplitude-frequency characteristics of a pantograph were derived. Based on the analysis of force fluctuation, the coupling relationship between pantograph parameters and droppers was obtained. Then the variation of the amplitude- frequency characteristics was analyzed by changing pantograph parameters individually. It is found the influence of the collector head’s mass and stiffness on the amplitude-frequency characteristics is obvious. The coupling relationship in the pantograph- catenary simulation system was validated by observing the variation of contact force standard deviation with different mass and stiffness of the collector head respectively. Adjusting the pantograph parameters to make the frequency, at which the response on the amplitude-frequency curve reaches its minimum, be equal to the frequency of the droppers, the fluctuation of contact force would be lowered, which means the current collection quality is improved to some extent. The coupling relationship proposed can be referential to the design, selection and performance assessment of pantograph-catenary systems.

catenary; pantograph; amplitude-frequency characteristics; force fluctuation; coupling

国家自然科学基金高铁联合基金重点项目(U1134205);国家自然科学基金(51377136;51405401)

2015-07-09修改稿收到日期：2015-09-10

姜静 女，硕士生，1990年生

刘志刚 男，博士，教授,博士生导师，1975年生

U225.1

A DOI:10.13465/j.cnki.jvs.2016.14.022