FGM中厚圆板轴对称自由振动的打靶法求解
2016-10-17李清禄张靖华李世荣
李清禄, 张靖华, 李世荣
(1. 兰州理工大学 理学院,兰州 730050; 2. 扬州大学 建筑科学与工程学院,江苏 扬州 225127)
FGM中厚圆板轴对称自由振动的打靶法求解
李清禄1, 张靖华1, 李世荣2
(1. 兰州理工大学 理学院,兰州730050; 2. 扬州大学 建筑科学与工程学院,江苏 扬州225127)
研究了由陶瓷和金属两种材料组成的功能梯度材料(FGM)中厚圆板的自由振动问题。基于考虑横向剪切变形中厚板的几何方程、物理方程及平衡方程,建立了以中面转角和横向位移为基本未知量的功能梯度中厚圆板轴对称自由振动问题的控制方程;假定功能梯度中厚圆板的材料性质方向按照幂函数连续变化规律;采用打靶法数值求解所得非线性两点边值问题出,获得了多种边界下功能梯度中厚圆板的无量纲自然频率以及振动模态。讨论了材料梯度指数、板的厚度以及边界条件对自然频率的影响。
功能梯度材料;中厚圆板;自由振动;频率;打靶法
功能梯度材料(Functionally Graded Material,FGM) 是一种非均质复合材料[1],在航空航天、汽车、生物及核工业等领域有广阔的应用前景。同时,由于该种材料在结构中各组分呈连续变化,不存在明显的界面与性能的突变,因此具有优于一般层叠型功能材料的特性。由于材料性质在横向的非均匀性导致了功能梯度结构的应力在横向分布的复杂性,表现出与均匀材料结构不同的特性。从而,使得FGM 结构的弯曲、屈曲和振动等宏观力学行为的分析要比相应的均匀材料结构复杂得多。近年来,FGM结构已引起国际学术界的广泛关注[2-4]。
对于薄板的振动问题的经典理论是基于Kirchhoff假设基础上的。随着板的厚跨比的增加,经典理论的结果将会出现比较大的误差。文献[5]对中厚板理论的适用范围作了详细研究,薄板和中厚板的分界线一般厚跨比=0.1,此后薄板理论解和中厚板理论解的误差越来越大;而中厚板和厚板的分界线应当在厚跨比=0.2处。侯宇等[6]利用H变换求解了厚圆板的轴对称振动的各阶固有频率。徐旭等[7]从三维弹性力学基本方程出发,利用初函数法研究了厚圆板轴对称振动的弹性力学解。人们将熟悉的针对均匀材料结构而发展起来的理论分析方法和数值计算手段推广应用于FGM 结构的宏观力学行为分析,研究FGM 结构的静动态响应,考察材料非均匀特性对结构力学行为的影响。李世荣等[8]研究了材料性质沿横向连续变化的功能梯度材料圆板的静态弯曲问题,给出了两种圆板弯曲解之间的相似转换关系。WANG等[9]利用三维弹性理论研究了轴对称FGM薄圆板的自由振动问题,得到了弹性简支和刚性滑动两种边界条件下的三维精确解。KERMANI等[10]利用三维弹性理论建立了FGM圆板和圆环板的自由振动控制方程,利用微分求积法求解了问题的数值解,讨论了厚径比和梯度指数对无量纲频率的影响。张弛等[11]用无网格法分析了功能梯度材料圆板的自由振动,并讨论了相关参数对结果的影响。文献[12]利用微分求积法研究了双参数弹性地基上FGM薄至中厚环板在热环境中的自由振动问题。
由上述文献知,许多学者采用不同方法研究了FGM圆板的静动态力学响应,而功能梯度材料中厚板的自由振动方面的研究相对较少。本文基于高阶剪切板理论,研究功能梯度中厚圆板的自由振动问题,建立了以中面转角和横向位移为基本未知量的功能梯度中厚圆板轴对称自由振动问题的控制方程,采用打靶法求解所得非线性常微分方程。讨论不同剪切理论下,材料梯度指数、厚径比以及边界条件对圆板自振频率的影响。
1 控制微分方程
考虑图1所示的功能梯度材料中厚圆板。设板的厚度h;半径为R。采用极坐标系(r,θ,z),其中r为径向;θ为环向;z坐标垂直于r-θ面。研究其轴对称自由振动问题。
考虑功能梯度材料圆板是由金属和陶瓷两相材料组成,假设梁的材料性质沿厚度方向按幂函数变化,即
(1)
目前,用来确定FGM有效材料性质的模型主要有Voigt混合率模型以及Mori-Tanaka模型。文献[13]详细研究了两种模型对振动频率的影响,结果表明:对于线性频率,两种模型计算的结果十分接近,而对于非线性振动,两种模型下的频率差异可以忽略。基于此,这里采用相对简单的Voigt混合率模型。其弹性模量、密度可表示为:
(2)
(3)
式中:下标m和c分别表示金属和陶瓷材料的物性参数;非负实数p为材料梯度指标。文献[14]研究表明材料泊松比对自由振动的频率几乎没有影响,可表示为:
v(z)=v
(4)
由图1可知,径向位移为u;横向位移为w。若只考虑横向振动,中厚圆板位移场可写为:

图1 FGM圆板示意图Fig.1 Sketch map of the FGM circular plate

(5)
式中:ψ为板中面法线的转角;t为时间变量。
几何方程:
(6)
物理方程:
(7)
将式(6)代入式(7),物理方程可进一步写为:
(8)
沿板的厚度方向积分,可得圆板弯矩和剪力为:
(9)
(10)
(11)
式中:κs为剪切修正系数;对Hencky板,κs=1;Reissner板,κs=6/5;Mindlin板,κs=12/π2。
运动方程:
动能为
(12)
势能为

(13)
根据Hamilton原理,问题的泛函为:
(14)
由变分δΠ=0得:
将式(6)代入上面的表达式
(15)
利用式(2),式(15)中刚度系数的定义为:
(16)
令Er=Em/Ecρr=ρm/ρc,通过积分可得:
(17)
对于板的自由振动,假设其位移和转角是时间的谐响应模态
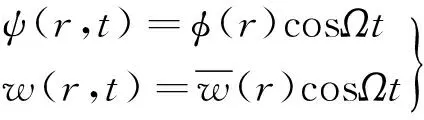
(18)

将式(18)代入式(15), 得到振型函数表示的位移形式的中厚圆板运动方程:

(19)
(20)
采用无量纲变换
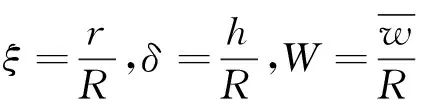
得FGM中厚圆板轴对称无量纲控制方程为:

2 边界条件
周边固定:ξ=1处,φ=0,W=0





3 数值结果与分析
式(21)和边界条件构成两点边值微分问题,这里采用打靶法[15]求其数值解。
为了和文献[14]计算的FGM圆板的计算结果进行比较,本文中也考虑金属材料Aluminiun(Al),陶瓷材料Alumina(Al2O3)构成的功能梯度材料厚圆板,其物性参数分别为:Em=70 GPa,ρm=2 700 kg/m2,Ec=380 GPa,ρc=3 800 kg/m2,v=0.3。
首先计算了材料梯度指数p=0,即均匀各项同性材料中厚圆板的前三阶固有频率。表1~表4给出了Hencky理论、Reissuer理论和Mindlin理论下,三种常见边界条件下前三阶固有频率的数值解,并和经典理论以及文献[6]和文献[16]计算的结果进行了比较。
由于目前文献中只有文献[16]给出了四阶以上的无量纲固有频率,且是Mindlin理论解。因此表4对本文的计算结果与文献[16]的比较结果作了比较,其结果十分接近,说明了本文计算的可靠性和计算程序的正确性。
从计算结果看出,本文的计算结果与已知文献的结果是非常接近的,经典理论下计算得到的结果只能适用于薄圆板,对于中厚圆板必须采用Reissuer-Mindlin理论。
需要说明的是,打靶法的计算效率和精度取决于变步长Runge-Kutta方法和Newton-Raphson迭代法的计算精度。与有限元法、微分求积法等相比,打靶法在求非线性常分方程两点边值问题时具有无可比拟的优越性,因为它不依赖于网格划分。另外,这种算法对步长在合理的范围内不敏感,容易实现,所以费时少而精度高。
表5~表7分别给出了周边固定、简支和自由三种边界条件下,中厚圆板厚径比δ=0.1,0.2和0.3,材料梯度指标p=0,0.1,0.5,1,2和5时,功能梯度圆板轴对称自由振动的前三阶无量纲固有频率。从表5~表7可知,当梯度指标一定时,无量纲固有频率随厚度δ的增加而降低;当厚度一定时,不同梯度指标下,中厚板的无量纲固有频率随梯度指标p的增大而减小。因此,对于中厚圆板,厚径比以及材料梯度指标对固有频率的影响很大。
目前,FGM中厚圆板自由振动的固有频率在已知出版的文献上还没有发现。我们将计算的结果和文献[14]进行比较,特别说明的文献[14]是基于经典板理论利用Rayleigh-Ritz法计算的,没有考虑剪切变形,其固有频率是薄圆板的。因此,表5~表7中只对厚度δ=0.1的计算结果和文献[14]计算结果进行了比较。不难看出,本文的结算结果和其十分接近,再次说明打靶法研究本问题的适用性。

表1 厚板自由振动无量纲一阶频率ω1(n=0,ν=0.3,δ=0.2)

表2 厚板自由振动无量纲二阶频率ω2(n=0,ν=0.3,δ=0.2)

表3 厚板自由振动无量纲三阶频率ω3(n=0,ν=0.3,δ=0.2)

表4 厚板自由振动无量纲四阶频率ω4(n=0,ν=0.3,δ=0.2)

表5 周边固支FGM厚板自由振动无量纲固有频率ωn
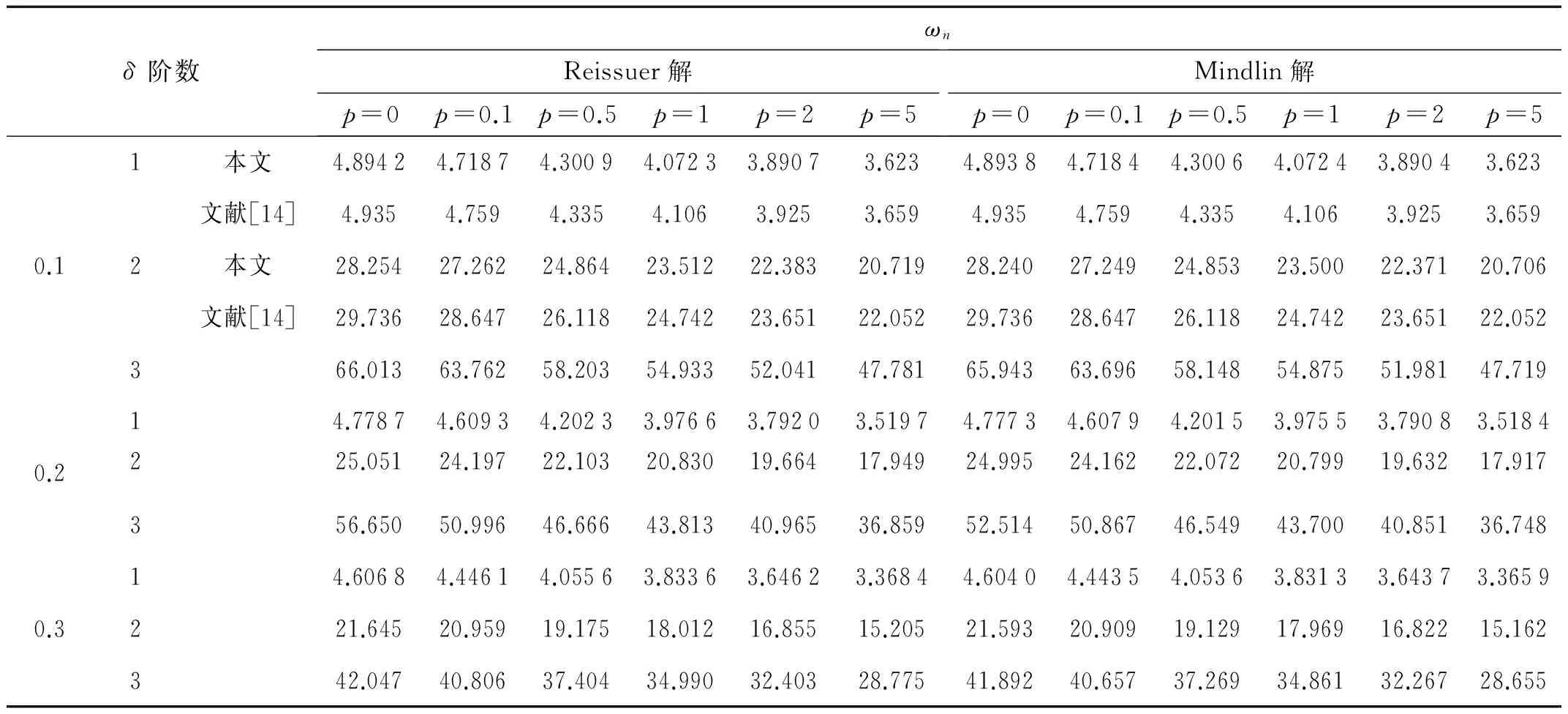
表6 周边简支FGM厚板自由振动无量纲固有频率ωn
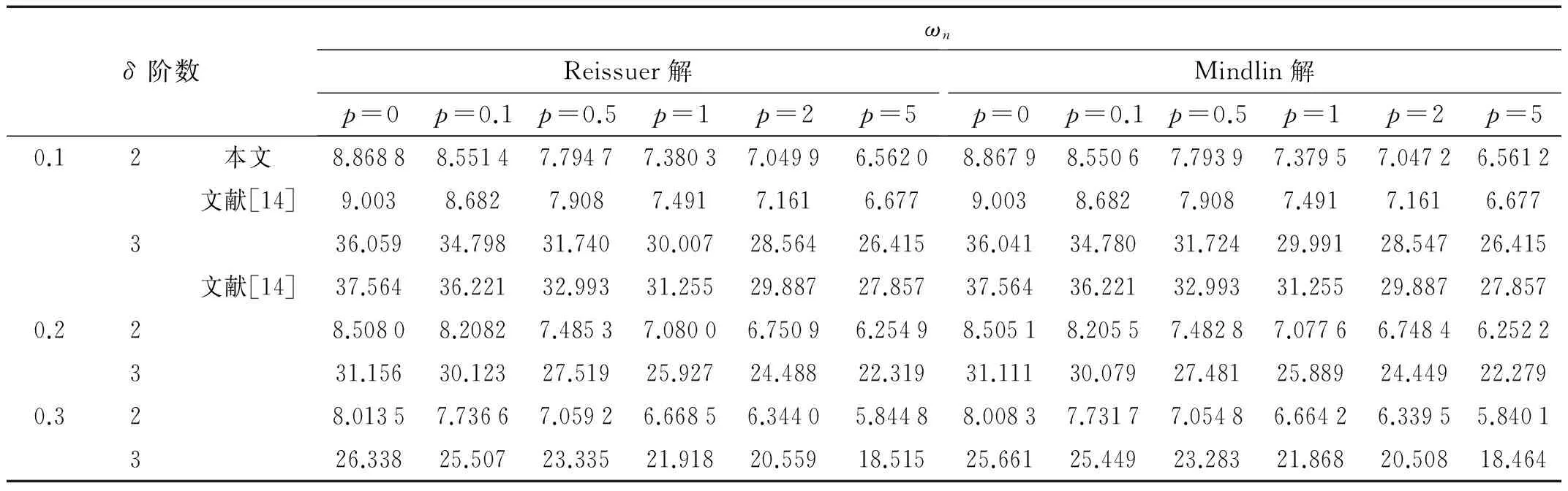
表7 周边自由FGM厚板自由振动无量纲固有频率ωn
图2为周边固定时,FGM厚圆板的1、2和3阶振动模态图,由图2可知,厚径比δ=0.2和0.3情况下振动模态图非常接近,而且与边界条件吻合的很好。图3和图4分别给出了周边简支和自由边界条件下,厚径比δ=0.2,梯度指数p=0.2时的前三阶振动模态图。

图2 周边固定FGM圆板自由振动模态图 Fig.2 Anterior third-order modes of FGM moderately thick circular plate with clamped edge

图3 周边简支FGM圆板自由振动模态图Fig.3 Anterior third-order modes of the FGM moderately thick circular plate with simply supported edge

图4 周边自由FGM圆板自由振动模态图Fig.4 Anterior third-order modes of the FGM moderately thick circular plate with free edge
4 结 论
基于考虑横向剪切变形中厚板的几何方程、物理方程及平衡方程,建立了以中面转角和横向位移为基本未知量的功能梯度中厚圆板轴对称自由振动问题的控制方程。利用打靶法求解了传统三种边界条件下的自由振动无量纲频率,将得到的结果与已有结果进行了比较,显示了打靶法求解两点边值问题的优越性,得到了高精度的数值结果。结果表明:
(1) 边界条件对中厚圆板的自振频率有较大影响,固定边界下的最大,自由边界下的最小。
(2) 随厚径比的增加(即板越厚),自振频率减小。
(3) 对于中厚圆板,自振频率随梯度指数的增大而减小。
(4) 三种厚板理论下计算的结果比较发现,Reissuer和Mindlin理论下的结果比较接近,而Hencky理论解偏大,因此对于中厚板,一般建议用Reissuer-Mindlin理论。
[1] KOIZUMI M. The concept of FGM ceramic transitions[J]. Functionally Gradient Materials,1993, 34:3-10.
[2] BHANGAL E R K, GANESAN N. Thermoelastic buckling and vibration behavior of a functionally graded sandwich beam with const rained viscoelastic core [J] . Journal of Sound and Vibration,2006,295:294-316.
[3] YANG J, SHEN H S. Non-linear analysis of functionally graded plates under transverse and in plane loads [J]. International Journal of Non-linear Mechanics, 2003,38(4): 467-482.
[4] 仲政, 吴林志, 陈伟球. 功能梯度材料与结构的若干力学问题研究进展[J]. 力学进展, 2010, 40(5): 528-541.
ZHONG Zheng, WU Linzhi, CHEN Weiqiu. Progress in the study on mechanics problems of functionally graded materials and structures [J]. Advances in Mechanics, 2010, 40(5): 528-541.
[5] 龙述尧, 姜琛. 中厚板理论的适用范围和精确程度的研究[J]. 湖南大学学报(自然科学版), 2012, 39(1): 37-41.
LONG Shuyao, JIANG Chen. Research on the applicable range and accuracy of moderately thick plate theory[J]. Journal of Huan University(Natural Science), 2012, 39(1): 37-41.
[6] 侯宇, 何福保. 厚圆板的轴对称振动[J]. 中国计量学院学报, 1995(增刊1):75-80.
HOU Yu, HE Fubao. Symmetrically free vibration of thick circular plates[J]. Journal of China Institute of Metrology, 1995(Sup1): 75-80.
[7] 徐旭, 何福保. 厚圆板轴对称振动的弹性力学解[J]. 力学季刊, 2000, 21(1): 59-65.
XU Xu, HE Fubao. Elasticity solution for axisymmetric vibration problem of thick circular plate[J]. Chinese Quarterly of Mechanics, 2000, 21(1): 59-65.
[8] 李世荣, 张靖华, 徐华. 功能梯度与均匀圆板弯曲解的线性转换关系[J]. 力学学报, 2011, 43(5): 871-877.
LI Shirong, ZHANG Jinghua, XU Hua. Linear transformation between the bending solutions of functionally graded and homogenous circular plates[J]. Chinese Journal of Theoretical and Applied Mechanics, 2011, 43(5):871-877.
[9] WANG Y, XU R Q, DING H J. Free axisymmetric vibration of FGM circular plates[J]. Applied Mathematics and Mechanics, 2009, 30(9): 1077-1082.
[10] KERMANI I D, GHAYOUR M, MIRDAMADI H R. Free vibration analysis of multi-directional functionally graded circular and annular plates[J]. Journal of Mechanical and Technology, 2012, 26(11): 3399-3410.
[11] 张弛,校金友, 张硕. 用无网格法分析功能梯度材料圆板的自由振动[J]. 科学技术与工程, 2014, 14(13): 145-150.
ZHANG Chi, XIAO Jinyou, ZHANG Shuo. Study on free vibration FGM plate by meshless method[J]. Science Technology and Engineering, 2014, 14(13): 145-150.
[12] MALEKZADEH P, GOLBAHAR H M R, ATASHI M M. Free vibration analysis of elastically supported functionally graded annular plates subjected to thermal environment[J]. Meccanica, 2011, 46:893-913.
[13] SHEN H S, WANG Z X. Assessment of Voigt and Mori-Tanaka models for vibration analysis of functionally graded plates[J]. Composite Structures, 2012, 94: 2197-2208.
[14] PRADHAN K K, CHAKRAVERTY S. Free vibration of functionally graded thin elliptic plates with various edge supports[J]. Structural Engineering and Mechanics, 2015, 53(2): 337-354.
[15] LI S R, TENG Z C, ZHOU Y H. Free vibration of heated euler-bernoulli beams with thermal post-buckling deformations[J] . Journal of Thermal Stresses, 2004, 27: 843-856.
[16] IRIE T, YAMADA G, TAKAGI K. Natural frequencies of thick annular plates[J]. Journal of Applied of Mechanics, 1982, 49(3):633-638.
Numerical solution of the free vibration of functionally graded material moderately thick circular plates by shooting method
LI Qinglu1, ZHANG Jinghua1, LI Shirong2
(1. School of Sciences, Lanzhou University of Technology, Lanzhou 730050, China;2. College of Civil Science and Engineering, Yangzhou University, Yangzhou 225127, China)
The free vibration of FGM moderately thick circular plates was investigated. A FGM plate consisting of metal and ceramic was considered in the study. Based on the geometric equation, physical equation and equilibrium equation of thick plates, taking into account the transverse shearing deformation, the free vibration equation of axisymmetric FGM thick circular plates was derived in terms of the middle surface angles of rotation and lateral displacement. The material properties of the plate were assumed to vary continuously in the thickness direction according to a power law. By using the shooting method to solve the coupled ordinary differential equations with different boundary conditions, the natural frequencies of FGM thick circular plates were obtained numerically. The effects of material gradient property, thickness ratio and boundary conditions on the natural frequencies were discussed in detail.
functionally graded material(FGM); moderately thick circular plates; free vibration; natural frequency; shooting method
国家自然基金( 11272278;11262010);甘肃省自然基金(1212RJZA028)
2015-06-19修改稿收到日期:2015-08-19
李清禄 男,博士,副教授,1974年生
E-mail:lqu2008@163.com
O343.7
A DOI:10.13465/j.cnki.jvs.2016.14.016
