基于有限元法的弓网过渡段处动态性能仿真分析

杨　艺， 周　宁， 李瑞平， 张卫华(西南交通大学 牵引动力国家重点实验室,成都　610031)



基于有限元法的弓网过渡段处动态性能仿真分析

杨艺， 周宁， 李瑞平， 张卫华(西南交通大学 牵引动力国家重点实验室,成都610031)

针对城市轨道交通铁路中采用的接触网锚段关节、刚柔过渡段及CED125D受电弓结构，基于ANSYS有限元软件，采用广州地铁实际接触网线路的基本参数，建立包含刚性接触网、柔性接触网及刚柔过渡段的接触网模型以及简化为弹簧阻尼机构的CED125D受电弓归算质量模型。通过动力学仿真分析得到反映弓网系统动态性能的接触压力与抬升位移等数据，进而对受电弓在通过锚段关节、刚柔过渡段时的动力学行为及规律进行探讨与研究。与实测结果比较，所建立的弓网系统有限元模型是正确和有效的。

锚段关节；刚柔过渡段；弓网耦合动力学；接触压力；抬升位移

当今社会，随着电气化铁路的发展，以及世界各地对环境问题的日益关注，各地都在大力发展城市轨道交通。由于环境条件的限制，城市轨道交通接触网经常同时使用刚性接触网与柔性接触网，以很多地铁交通为例，在隧道段使用刚性接触网，明线段则使用柔性接触网，存在着锚段关节以及刚柔过渡段等不同的线路条件。因此考虑受电弓在通过这种不同线路条件时的动力学行为，对弓网关系的研究有重要的意义。

基于ANSYS有限元软件，根据广州地铁实际接触网线路参数建立了包含刚性接触网、柔性接触网及刚柔过渡段的接触网模型，采用CED125D受电弓三质量块归算质量模型，通过仿真分析计算了受电弓在通过不同线路条件时弓网接触点的抬升位移、接触压力等动态性能参数，并就受电弓在通过锚段关节、刚柔过渡段时的动力学行为以及规律进行了讨论。最后将仿真结果与线路实测结果进行比较，验证了本文建立的城市轨道交通中弓网系统模型的准确性和有效性。

1　接触网模型

1.1柔性段和刚性段模型

对于接触网柔性段，采用有限单元法，将接触线和承力索等效为梁单元，而吊弦相对前二者来说，线密度较小，简化为弹簧质量单元，从而建立包括承力索、接触线和吊弦的柔性接触网模型[1-4](见图1(a))，模型的参数见表1；刚性悬挂接触网由接触线、汇流排及悬挂机构组成，将悬挂机构考虑为有自重的弹簧，汇流排与接触线一起考虑为梁单元[5](见图1(b))，模型的参数见表2。

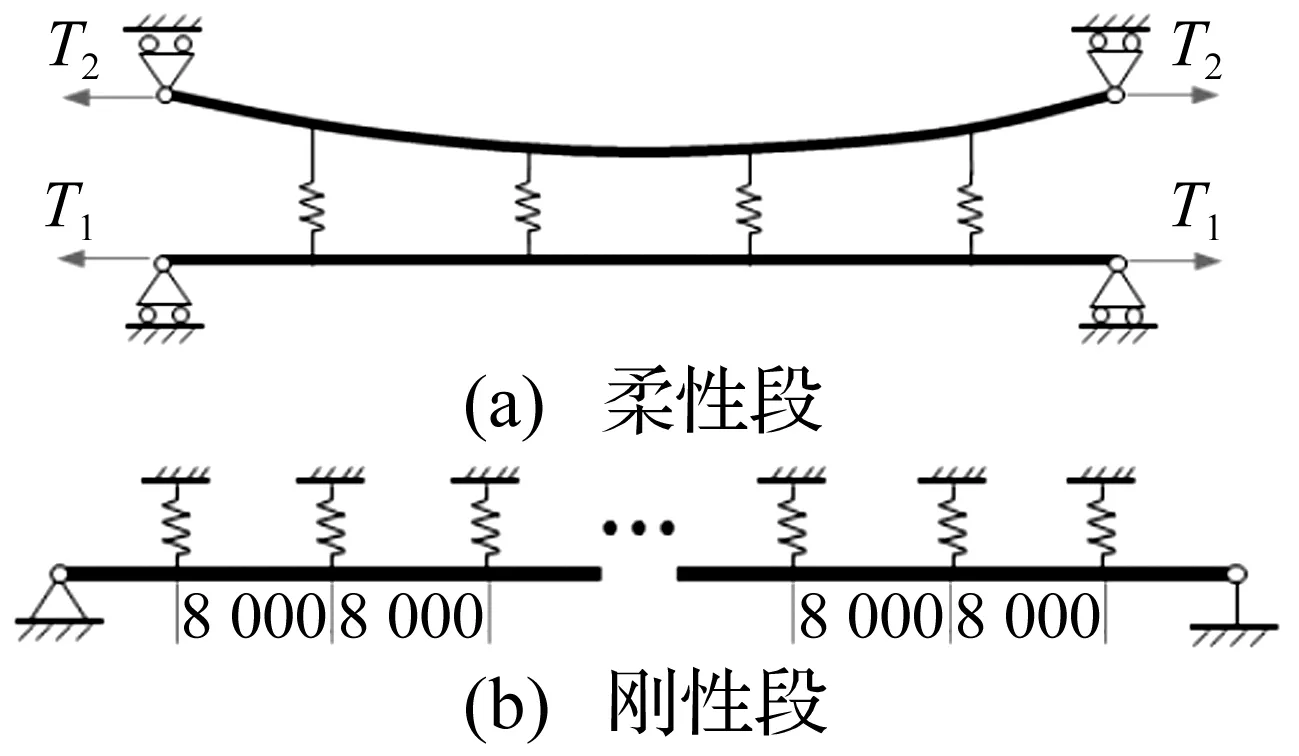
图1　接触网柔性段和刚性段模型Fig.1　Flexible suspension and rigid suspension catenary

表1　接触网柔性段仿真参数

表2　接触网刚性段仿真参数

1.2锚段关节模型

两个相邻锚段的衔接区段(重叠部分)称为锚段关节，是为了使受电弓能平滑、安全地由一个锚段过渡到另一个锚段而设计的[6]。采用与刚性接触网类似的建模方法，将两个锚段的悬挂机构等效为弹簧-质量系统，用带质量的弹簧单元combine14和mass21进行网格划分。接触线和汇流排一同视为梁结构，选用beam188划分相应网格。同时，将梁结构的末端抬高70 mm，并在两个锚段端部形成有部分重叠的平行分布(见图2)。

1.3刚柔过渡模型

刚柔过渡段是指刚性接触网与柔性接触网的衔接过渡处，是实现刚柔无缝连接的关键部位，主要分为关节式和贯通式两种[7-9]。对于贯通式刚柔过渡段，采用刚性逐渐减小的切槽式汇流排与柔性接触线相衔接来实现刚柔过渡的。首先建立上述的刚性段和柔性段模型，然后通过定义一系列截面积逐步减小的梁单元(beam188)，以模拟切槽式汇流排，并实现刚性接触网到柔性接触网刚度的自然过渡，从而建立贯通式刚柔过渡模型(见图3)。

关节式刚柔过渡，采用柔性接触线和刚性汇流排平行架设形成锚段关节来实现刚柔过渡。即柔性悬挂与刚性悬挂平行交叉一段，形成类似关节的形式。在刚柔过渡的切入点处，刚性接触网与柔性接触网分开，刚性接触网导高高于柔性接触网导高20～50 mm(导高差)，具体值根据受电弓经过刚柔段弓头抬升的变化决定(见图4)。

图2　刚性接触网锚段关节模型(mm)Fig.2　Model of overlap span(mm)

图3　贯通式刚柔过渡段模型Fig.3　Run-through transition section

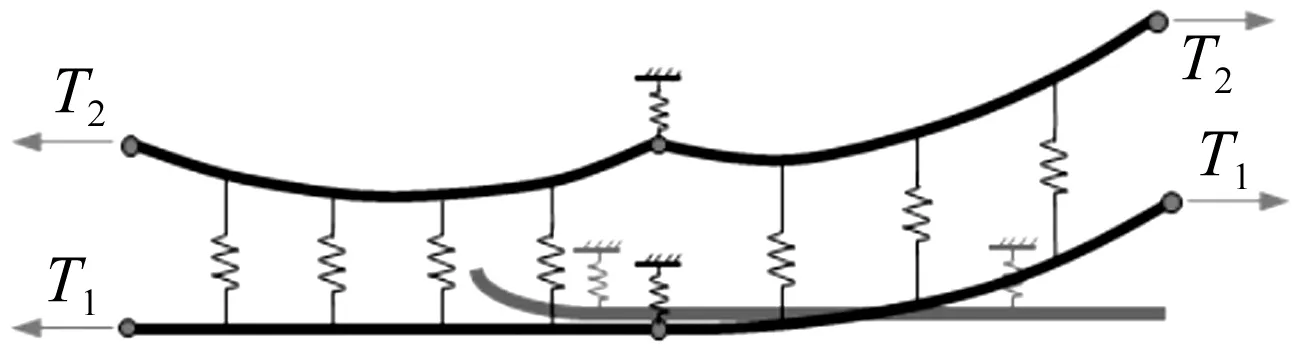
图4　关节式刚柔过渡段模型Fig.4　Joint transition section

2　受电弓模型

在本文的研究中，只考虑弓网之间的垂向运动，因此将CED125D型受电弓简化为三质量块归算模型[10](见图5)，归算参数见表3。

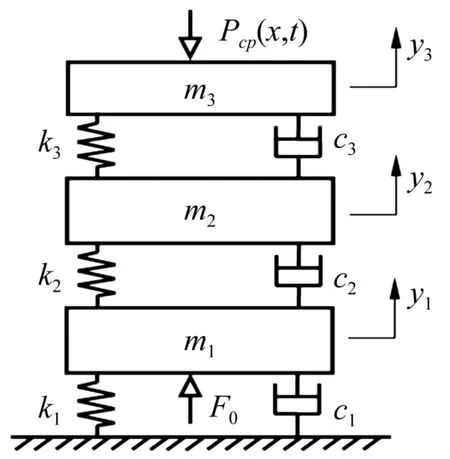
图5　受电弓归算质量模型Fig.5　Model of pantograph

由图5可知，从上到下依次是：m3,c3,k3分别为弓头部分的等效质量、等效阻尼、等效刚度；m2,c2,k2分别为上框架部分的等效质量、等效阻尼、等效刚度；m1,c1,k1分别为下臂杆部分的等效质量、等效阻尼、等效刚度；Pcp(x,t)为接触网与受电弓之间的动态接触压力；F0为受电弓受到的静态抬升力。

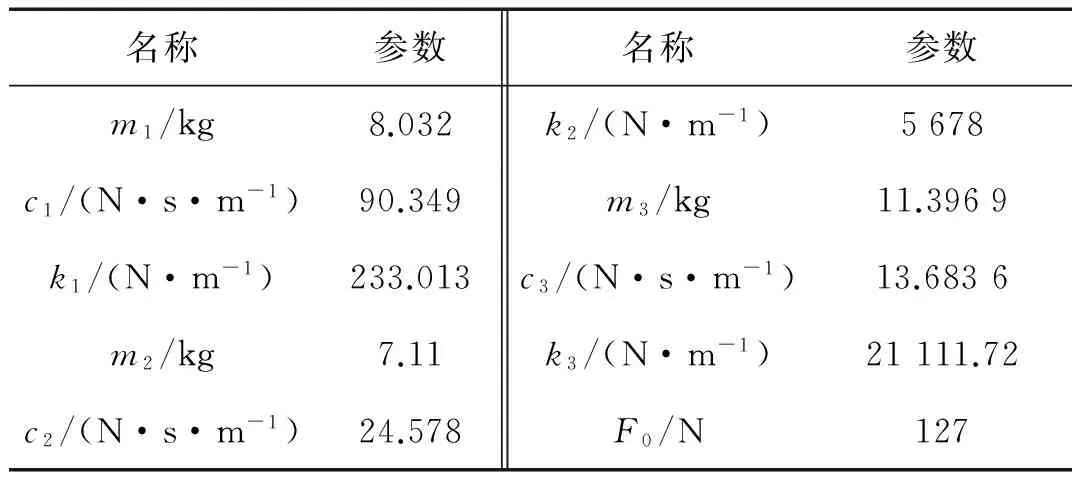
表3　受电弓结构参数

3　动力学计算结果

3．1在锚段关节处的弓网动态行为

考虑受电弓分别以60 km/h 、80 km/h、100 km/h这三种速度工况沿接触网运动，设采样频率为1 000 Hz，由此得到受电弓通过时接触网的抬升位移和弓网之间的接触压力(见图6)。

图6　锚段关节弓网接触力及弓头位移结果Fig.6　Simulation results in overlapping section

由图6可知,当受电弓通过锚段关节时，弓网之间的接触压力产生明显的波动，随着速度的增加，锚段关节处弓网间的最小接触力从60 km/h的32.63 N减小到100 km/h的0 N；最大接触力从60 km/h的158.18 N增大到100 km/h的193.91 N，而且弓网间的接触压力的震荡也逐渐增大。当速度达到100 km/h时，锚段关节处的接触力震荡剧烈，发生了离线现象。同时可见，刚性接触网在受电弓通过时的动态抬升量非常小，基本在1～5 mm之间波动，在锚段关节处由于接触网重叠处刚度的增加，弓头的振动位移有减小的趋势。

3．2贯通式刚柔过渡段处的弓网动态行为

对于贯通式刚柔过渡段，考虑受电弓从柔性段进入到刚性段和从刚性段进入到柔性段两种通过情况，在速度80 km/h、120 km/h、140 km/h条件下进行弓网系统动力学计算，时间积分步长为0.002 s，由此得到受电弓通过时接触网的抬升位移和弓网之间的接触压力，其结果见图7。

由图7可知：当受电弓经过刚柔过渡段时，由于接触网刚度存在较大的差异，从而导致弓网接触力在过渡段产生明显的波动。在同一速度等级下，受电弓从柔性段进入刚性段时，接触力的波动幅度明显要比从刚性段进入柔性段时大；对比不同速度等级受电弓从柔性段进入刚性段的接触压力发现,随着速度的增加，接触压力的波动逐渐增大。当速度为80 km/h时，过渡段的接触压力在49.98～188.12 N之间，未出现离线；当速度增加到140 km/h时，过渡段的接触压力在0～259.70 N之间震荡，产生离线现象。但在此速度下，受电弓从刚性接触网段过渡至柔性段未出现离线，仍能实现良好的过渡。

另一方面，从弓头振动位移来看，由于刚性区段接触网的静态刚度远大于柔性区段，所以在刚性段以及刚柔过渡段受电弓的弓头位移明显小于柔性段的弓头振动位移。

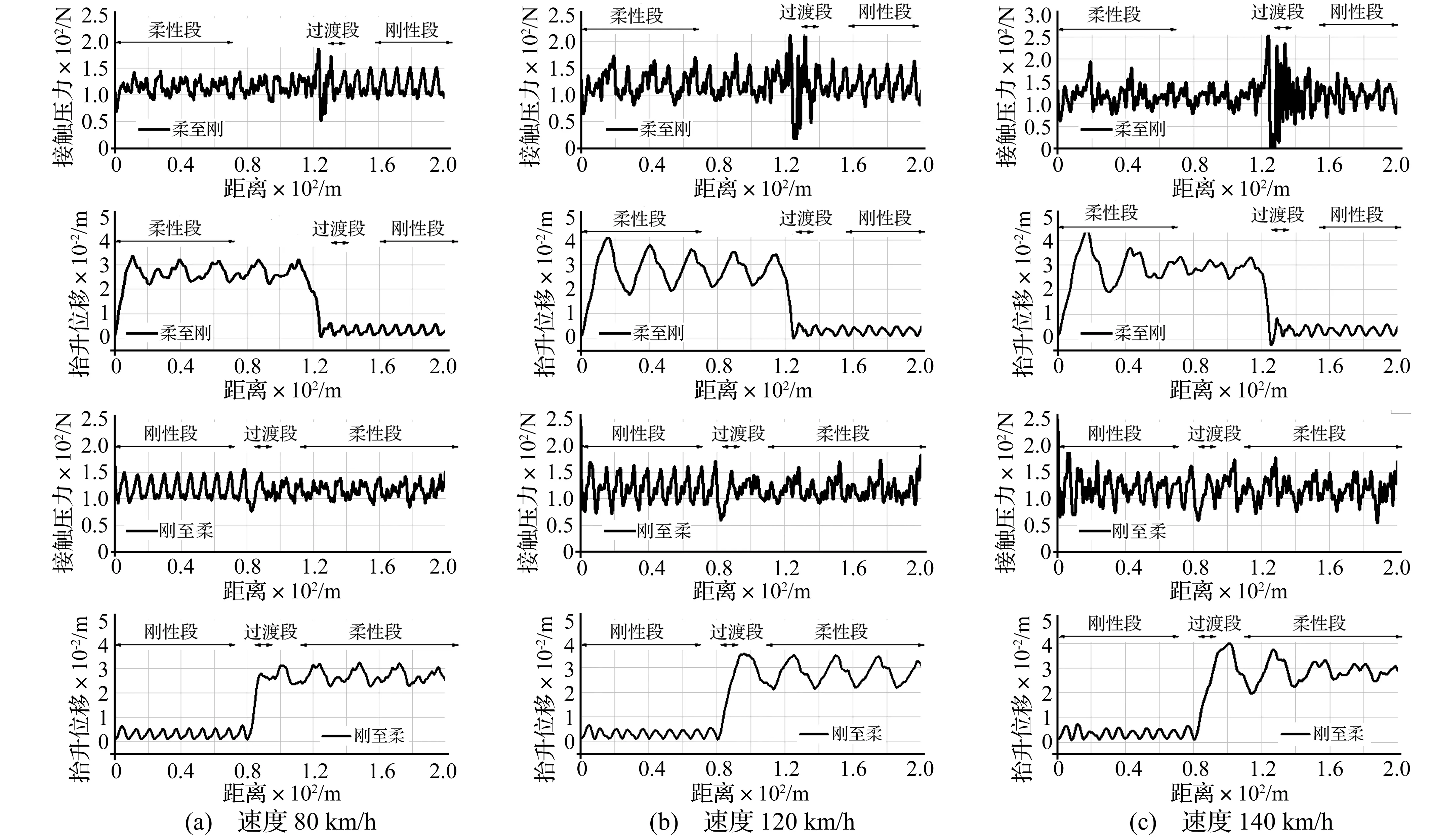
图7　贯通式刚柔过渡弓网接触力及弓头位移结果Fig.7　Simulation results in Run-through transition section

3．3关节式刚柔过渡段处的弓网动态行为

对于关节式刚柔过渡段模型，为研究不同导高差对过渡段处接触力的影响，以下分别对30 mm、40 mm及50 mm这三种导高差工况进行计算。首先考虑受电弓从柔性段进入到刚性段情况，在速度等级80 km/h条件下，其仿真结果见图8。

从图8可知，导高差为30 mm时，在过渡段附近弓网接触力在0～275 N之间，波动很大，产生了弓网离线；导高差为40 mm时，弓网接触力在18～156 N之间，波动减小，离线现象消失；导高差为50 mm时，弓网接触力在35～147 N之间，相对于导高差为40 mm时的接触力其波动更小。从抬升位移数据来看，导高差为30 mm时，过渡段附近处接触网的抬升位移出现了一个较陡的峰值，随着导高差的增加，该峰值逐渐平缓，使得受电弓可以平稳过渡。因此，从仿真结果中可以看到适当的增加导高差有利于受电弓从柔性段顺利过渡到刚性段。

在导高差30 mm时，受电弓从柔性接触网过渡到刚性接触网有明显的离线。在这种不利条件下，探究受电弓从刚性接触网过渡到柔性接触网时的情况。使用同样的仿真参数，考虑受电弓从刚性段进入柔性段，在速度等级80 km/h、120 km/h以及160 km/h条件下进行动力学计算(见图9)。

图8　速度80 km/h时关节式刚柔过渡弓网接触力及弓头位移结果Fig.8　Simulation results in joint transition under different height difference, at 80 km/h

图9　导高差30 mm时关节式刚柔过渡弓网接触力及弓头位移结果Fig.9　Simulation results in joint transition section with the height difference of 30 mm

从图8和图9可知，导高差为30 mm时，虽然受电弓从柔性段进入到刚性段时弓网发生了明显的离线现象，但从刚性段进入到柔性段时，过渡段的接触压力在40～205 N之间，弓网没有发生离线，过渡比较顺利。同样，弓头位移在受电弓通过过渡段时，由于接触网整体刚度的差异，产生一个较大的峰值，并且随着速度的增加，峰值呈减小趋势。

4　线路实验验证

为了验证本文对刚性悬挂接触网仿真方法的准确性，将受电弓以80 km/h速度运行工况下仿真分析得到的接触压力的统计值与广州地铁线路实测的接触压力统计值进行了对比分析(见表4)。

表4　80 km/h工况下接触压力统计值比较

由表4可知：本仿真过程中，CED125D受电弓以80 km/h的速度运行时，弓网系统的平均接触力为125.63 N，在83.40～173.31 N之间波动。为便于实测结果进行比较，根据EN50318标准[11]，将实测数据频率的取值范围设置为0～20 Hz。通过与实测数据进行比较，可知本文所得的平均接触力等参数与实测结果较吻合，虽然存在一定的差异，但总体结果是令人满意的。

5　结　论

针对包含锚段关节、刚柔过渡段的接触网和CED125D受电弓结构，基于有限元法建立了接触网和受电弓的弹簧阻尼结构模型，计算了影响弓网系统动态性能的接触力、抬升位移等指标。从而得出以下结论：

(1) 锚段关节处弓网之间的接触压力会发生明显的变化，接触力的波动随速度的增加而变大，当速度升高至100 km/h时，弓网之间出现离线现象。

(2) 对于贯通式刚柔过渡，弓网接触压力的波动幅值随着速度的增加而增加。在同一速度等级下，受电弓从刚性段进入到柔性段时的弓网动态特性要比从柔性段进入到刚性段好。在速度140 km/h时受电弓从柔性段过渡至刚性段时出现了离线现象。但在此速度下，受电弓从刚性段过渡至柔性段未出现离线，仍能实现良好的过渡。

(3) 对于关节式刚柔过渡，适当的增加导高差有利于受电弓从柔性段顺利过渡到刚性段，减少弓网离线。

[1] 周宁，张卫华. 基于直接积分法的弓网耦合系统动态性能仿真[J]. 中国铁道科学，2008，29(6):71-76.

ZHOU Ning，ZHANG Weihua.Dynamical performance simulation of the pantograph-catenary coupled system based on direct integration method[J]. China Railway Science,2008, 29(6):71-76.

[2] 李瑞平，周宁，梅桂明，等.初始平衡状态的接触网有限元模型[J].西南交通大学学报，2009,44(5)：732-737.

LI Ruiping，ZHOU Ning，MEI Guiming，et al. Finite element model for catenary in initial equilibrium state[J]. Journal of Southwest Jiaotong University，2009,44(5)：732-737.

[3] 张卫华, 沈志云. 接触网动态研究[J]. 铁道学报, 1991, 13(4): 26-33.

ZHANG Weihua，SHEN Zhiyun. Dynamic studies on catenary[J]. Journal of the China Railway Society, 1991, 13(4): 26-33.

[4] 李瑞平,周 宁,吕青松,等.横风环境中弓网动力学性能分析[J].振动与冲击,2014,33(24):39-44.

LI Ruiping, ZHOU Ning, LÜ Qingsong, et al. Pantograph-catenary dynamic behavior under cross wind[J]. Journal of Vibration and Shock,2014,33(24):39-44.

[5] 梅桂明，张卫华. 刚性悬挂接触网动力学研究[J]. 铁道学报，2003, 25(2): 24-29.

MEI Guiming，ZHANG Weihua. Study on dynamics of rigid suspension catenary[J]. Journal of the China Railway Society,2003, 25(2): 24-29.

[6] KIESSLING F, PUSCHMANN R, SCHMIEDER A，et al. Contact lines for electric railways: planning, design, implementation, maintenance[M]. Paris: Publicis Corporate Publishing, 2009.

[7] WU T X, BRENNAN M J. Dynamic stiffness of a railway overhead wire system and its effect on pantograph catenary system dynamics[J]. Journal of Sound and Vibration, 1999, 219(3): 483-502.

[9] SHIMIZU M, KOBAYASHII T, OYA A. Development of transition structures between overhead rigid conductor line and catenary-type contact line[J]. Quarterly Report of RTRI, 2008, 49(2): 103-107.

[10] 周宁，张卫华，王冬. 受电弓等效模型参数识别及动态性能测试[J]. 西南交通大学学报，2011,46(3)：398-403.

ZHOU Ning, ZHANG Weihua, WANG Dong. Lumped mass model for dynamic performance simulation of pantograph[J]. Journal of Southwest Jiaotong University，2011,46(3)：398-403.

[11] Railway applications—current collection systems—validation of simulation of the dynamic interactionbetween pantograph and overhead contact line：EN 50318[S].Brussels:CENELEC,2002.

Dynamic performance analysis of different sections of overhead catenary based on finite element model

YANG Yi, ZHOU Ning, LI Ruiping, ZHANG Weihua

(Traction Power State Key Laboratory，Southwest Jiaotong University，Chengdu 610031，China)

For the overlapping section and transition section in the overhead catenary of urban rail transit (URT) as well as the CED125D pantograph, based on the ANSYS simulation platform and according to the practical parameters of catenary network of Guangzhou subway, an appropriate finite catenary model was established, which consists of the rigid suspension catenary, the flexible suspension catenary and the transition sections coupling with a three lumped mass model of the CED125D pantograph. By the dynamical simulations, the contact force and pantograph head displacement that reflect the dynamic performance of the pantograph-catenary system were obtained. Then the dynamic behaviors and the regular pattern of the pantograph-catenary system under the conditions that the pantograph goes through the different sections of catenary were analyzed. Comparing the simulation results provided with the field measured results, the correctness and the effectiveness of the model were proved.

overlapping section; transition section; pantograph-catenary coupling dynamics; contact force; lifted displacement

国家自然科学基金项目(5147539)；国家973计划项目(2011CB711105)

2015-06-07修改稿收到日期：2015-08-31

杨艺 女，硕士生，1991年生

张卫华 男，博士，教授，博士生导师，1961年生

U225.2

A DOI:10.13465/j.cnki.jvs.2016.14.012