一类时滞SIQS传染病模型的Hopf分支

刘　娟

(蚌埠学院数学与物理系，安徽 蚌埠　233030)



一类时滞SIQS传染病模型的Hopf分支

刘娟

(蚌埠学院数学与物理系，安徽 蚌埠233030)

研究了一类具有非线性发生率的时滞SIQSR传染病模型的Hopf分支，以模型中染病者和隔离者的临时免疫期时滞为分支参数，利用特征值方法得到模型局部渐近稳定和Hopf分支存在的充分条件，并通过实例验证了所得结果的正确性.研究表明，延迟Hopf分支的发生，可以有效控制疾病的传播.

SIQS模型；稳定性；Hopf分支；时滞

【引用格式】刘娟.一类时滞SIQS传染病模型的Hopf分支[J].北华大学学报(自然科学版)，2016，17(5)：561-565.

1　引　　言

为了有效控制传染病的传播，基于不同的疾病感染率学者们提出了很多不同的传染病模型.文献[1-2]分别研究一类具有双线性发生率的传染病模型，文献[3-5]分别研究了一类具有标准发生率的传染病模型.考虑到以上两种发生率在描述某些传染病传播机理时的局限性，不少学者提出并研究了具有非线性发生率的传染病模型[6-9].文献[6]提出了如下具有非线性发生率的时滞SIQS传染病模型：

(1)

显然，文献[6]是假设染病者和隔离者是瞬时向易感群体中转移的，即文献[6]忽略了模型中染病者和隔离者的临时免疫期时滞因素.因此，受文献[6]启发，本文研究另外一种形式的时滞SIQS传染病模型：

(2)

其中，τ是染病个体和隔离个体的临时免疫期时滞.本文主要研究时滞τ对模型(2)稳定性的影响，以时滞τ为分支参数，确定模型(2)Hopf分支存在的充分条件.

2　Hopf分支的存在性

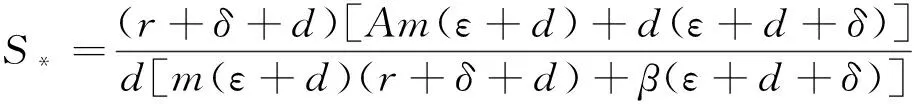
模型 (2)在地方病平衡点E*(S*，I*，Q*)处的线性化部分的特征方程为

λ3+p2λ2+p1λ+p0+(q2λ2+q1λ+q0)e-λτ+(s1λ+s0)e-2λτ=0，

(3)

其中

p0=(α2α3-α1α4)α6， p1=α1α4+α1α6+α4α6-α2α3，

p2=-(α1+α4+α6)， q0=α2α3β4+α3α6β1-α1α4β4-α1α6β3，

q1=β4(α1+α4)+β3(α1+α6)-α3β1， q2=-(β3+β4)，

s0=(α3β1-α1β3)β4， s1=β3β4，

α5=δ， α6=-d， β1=r， β2=ε， β3=-r， β4=-ε.

由此，城镇化对物流业能源消耗变动的影响可通过上述十大效应进行细致的刻画，从而更清晰地揭示城镇化对物流业能源消耗变动的影响。

当τ=0时，方程(3)变为

λ3+p02λ2+p10λ+p00=0，

其中，p00=p0+q0+s0，p01=p1+q1+s1，p02=p2+q2.

显然，如果条件 (H1)：p02>0，p02p01>p00成立，则根据Routh-Hurwithz稳定性判据可知，地方病平衡点E*(S*，I*，Q*)此时是局部渐近稳定的.

当τ>0时，在方程(3)的左右两边同时乘以eλτ，方程(3)变为

q2λ2+q1λ+q0+(λ3+p2λ2+p1λ+p0)eλτ+(s1λ+s0)e-λτ=0.

(4)

令λ=iω(ω>0) 为方程(4)的根，则有

从而得到

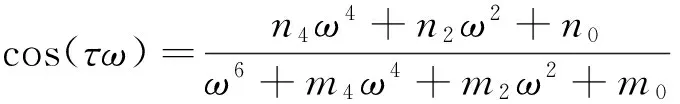
其中

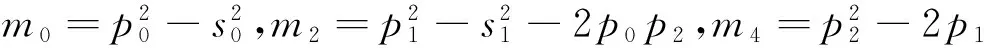
n0=(s0-p0)q0，n2=(p0-s0)q2-(p1-s1)q1+p2q0，n4=q1-p2q2，

n1=(p1+s1)q0-(p0+s0)q1，n3=p2q1-q0-(p1+s1)q2，n5=q2.

于是可以得到关于ω的下列方程

cos2(τω)+sin2(τω)=1.

(5)

如果模型(2)的系数全部给定，那么我们很容易利用Matlab软件计算得到方程(5)的根.所以，为了得到本文的主要结果，我们给出下列假设:

(H2) 方程(5) 至少存在一个正根.

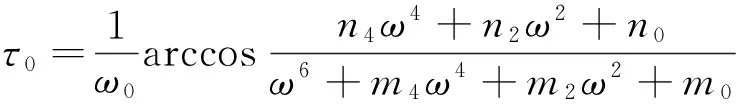
将λ(τ) 代入方程(3)并在方程(3)左右两边求λ关于τ的导数，得到

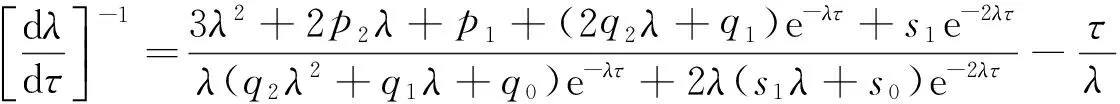
进而有

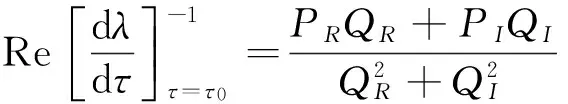
其中

PR=2q2ω0sin(τ0ω0)+q1cos(τ0ω0)+s1cos(2τ0ω0)，

PI=2q2ω0cos(τ0ω0)-q1sin(τ0ω0)-s1sin(2τ0ω0)，

定理1对于模型(2)，如果条件 (H1)和(H2)成立，那么当τ∈[0，τ0)时，地方病平衡点E*(S*，I*，Q*) 局部渐近稳定；当τ=τ0时系统(2)产生局部Hopf分支并在地方病平衡点E*(S*，I*，Q*)处产生一簇分支周期解.

3　仿真示例

为了对本文的理论结果进行验证，我们给出一个仿真示例.选取文献[6]中的一组相同的参数值，即A=100，β=0.05，m=1.1，d=0.2，r=0.1，δ=0.7，ε=0.3.则可以得到模型(2)的如下示例：

(6)

经过计算可以得到R0=25>1，进而得到系统(6)的唯一地方病平衡点E*(452.8，19.7，27.6)，并得到ω0=3.966 4和τ0=10.925 5.根据定理1可知，当τ∈[0，τ0)时，地方病平衡点E*(452.8，19.7，27.6)是渐近稳定的，如图1所示(选取τ=9.089 3).τ>τ0时，地方病平衡点E*(452.8，19.7，27.6)则失去稳定性，系统(6)产生Hopf分支并在E*(452.8，19.7，27.6)附近产生一簇分支周期解.如图2.

4　总　　结

本文基于文献[6]中所提出的时滞SIQS传染病模型，进一步考虑了染病者和隔离者的临时免疫期，并以临时免疫期时滞为分支参数，研究了另外一种形式的时滞SIQS传染病模型的Hopf分支问题.研究表明，临时免疫期时滞对模型的稳定性具有重要的影响作用.当时滞的取值适当小时，模型将处于一种理想的渐近稳定状态.而一旦时滞的取值超越了临界点τ0，模型将失去稳定性，产生Hopf分支.此时，不利于对疾病的传播进行控制，因此，应该采取有效措施尽量控制、延迟Hopf分支的产生.

[1]SongMei，MaWanbiao.AsymptoticpropertiesofarevisedSIRepidemicmodelwithdensitydependentbirthrateandtimedelay[J].DynamicsofContinuous，DiscreteandImpulsiveSystemsSeriesA：MathematicalAnalysis，2006，13(3)：199-208.[2]WenLuo-sheng，YangXiao-fan.StabilityandHopfbifurcationanalysisofaneco-epidemicmodelwithastagestructure[J].NonlinearAnalysis，2011，74(4)： 1088-1106.

[3]HuZhi-xing，LiuSheng，WangHui.StabilityandHopfbifurcationanalysisofaneco-epidemicmodelwithastagestructure[J].NonlinearAnalysis：RealWorldApplications，2008，9(5)：2302-2312.[4]YoshidaNaoki，HaraTadayuki.GlobalstabilityofadelayedSIRepidemicmodelwithdensitydependentbirthanddeathrates[J].JournalofComputationalandAppliedMathematics，2007，201 (2) ：339 -347.[5] 苟清明．一类具有阶段结构和标准发生率的SIS模型[J]．西南大学学报(自然科学版)，2007，29(9)： 6-13．

[6] 杨俊仙，徐丽.一类具非线性发生率和时滞的SIQS传染病模型的全局稳定性[J].山东大学学报(理学版)，2014，49(5)：67-74.

[7] 宫兆刚，杨柳，李浏兰.具有常数输入率的SIRS传染病模型的稳定性分析[J].应用数学，2013，26(3)：477-481.

[8] 杨秀香，程纪远，薛春荣.一类具有隔离干预的非线性传染率的传染病模型的全局稳定性分析[J].生物数学学报，2012，27(4)： 577-588．

[9] 周艳丽，张卫国.一类具有非单调传染率的SEIRS时滞传染病模型的全局稳定性[J].上海理工大学学报(自然科学版)，2014，36(2)：103-109.

[10]HassardBD，KazarinoffND，WanYH.TheoryandapplicationsofHopfbifurcation[M].Cambridge：CambridgeUniversityPress，1981.

【责任编辑：伍林】

Hopf Bifurcation of a Delayed SIQS Epidemic Model

Liu Juan

(Department of Mathematics and Physics，Bengbu University，Bengbu 233030，China)

Hopf bifurcation of a delayed SIQS epidemic model with nonlinear incidence is investigated.Sufficient conditions for local stability and the existence of Hopf bifurcation are established by regarding the time delay due to the temporary period of the infective and the quarantined individuals as the bifurcation parameter.Finally，a numerical example is also provided to verify the obtained results.It is found that the disease can be controlled by putting off the occurrence of the Hopf bifurcation.

SIQS model；stability；Hopf bifurcation；delay

1009-4822(2016)05-0561-05

10.11713/j.issn.1009-4822.2016.05.001

2016-03-27

安徽省高等学校省级自然科学研究项目(KJ2015A144).

刘娟(1979-)，女，副教授，主要从事生物数学研究，E-mail:my7216@163.com.

O175.12

A