两类非线性三阶四点边值问题解的存在性
2016-10-17林东海裴明鹤
林东海,裴明鹤
(北华大学数学与统计学院,吉林 吉林 132013)
两类非线性三阶四点边值问题解的存在性
林东海,裴明鹤
(北华大学数学与统计学院,吉林 吉林132013)
利用Leray-Schauder度理论,得到了非线性三阶微分方程x‴=f(t,x,x′,x″),t∈[0,1]分别满足下列四点边界条件x(0)=0,x′(0)=αx′(ξ),x′(1)=βx′(η)和x′(0)=αx′(ξ),x(1)=0,x′(1)=βx′(η)的两类边值问题解的存在性,并且作为应用给出了一个例子.
Leray-Schauder度理论;Nagumo条件;四点边值问题;存在性
【引用格式】林东海,裴明鹤.两类非线性三阶四点边值问题解的存在性[J].北华大学学报(自然科学版),2016,17(5):572-576.
1 引 言
本文考虑两类非线性三阶四点边值问题,即非线性三阶微分方程
x‴=f(t,x,x′,x″), t∈[0,1],
(1)
逐一满足下列四点边界条件
x(0)=0, x′(0)=αx′(ξ), x′(1)=βx′(η),
(2)
x′(0)=αx′(ξ), x(1)=0, x′(1)=βx′(η)
(3)
的边值问题解的存在性,这里f(t,x0,x1,x2)在[0,1]×3上连续,ξ,η∈(0,1),0<α≤1,0<β≤1,并且α+β≠2.
三阶微分方程出现于应用数学和物理学的许多领域,例如挠度具有常数或横断面发生变化的弯曲梁,三层梁以及电磁波或重力驱动流等[1-2].因此,三阶边值问题受到微分方程学者的广泛关注[1,3-17].而上述提到的成果大多是关于两点或三点边界条件的,而关于四点及其以上边界条件的成果较少见到[1,7,12-13].本文的目的是利用Leray-Schauder度理论,建立非线性三阶四点边值问题(1)-(2)和(1)-(3)的解的存在性结果.
2 主要结果
首先利用Leray-Schauder度理论建立非线性三阶四点边值问题(1)-(2)的解的存在性定理.
定理1假设
(ⅰ)f(t,x0,x1,x2)∈C([0,1]×3),并且对每一个固定的(t,x1,x2)∈[0,1]×2,f关于x0单调递减;
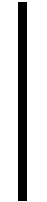
xf(t,x,x,0)>0;
(ⅲ)f(t,x0,x1,x2)满足Nagumo条件,即存在一个定义于[0,+)上的正值连续函数h(s),使得∀(t,x0,x1,x2)∈[0,1]×[-M,M]2×,有
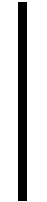
则三阶四点边值问题(1)-(2)至少存在一个解x=x(t)满足
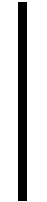
证明:首先验证下面的边值问题族
x‴=λf(t,x,x′,x″),t∈[0,1],λ∈[0,1],
(4)
x(0)=0,x′(0)=αx′(ξ),x′(1)=βx′(η),
(5)
在C2[0,1]中先验有界.为此,设x(t)是BVP(4)-(5)的任意一个解.我们将证明
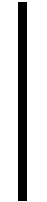
(6)
以及
(7)
首先证明
(8)
注意到,如果在方程(4)中λ=0,则BVP(4)-(5)只有平凡解,从而式(6)和(7)成立.因此可设λ∈(0,1].假设式(8)不成立,则存在t*∈[0,1],使得
x′(t*)>M或x′(t*)<-M.

x′(t0)x‴(t0)=λx′(t0)f(t0,x(t0),x′(t0),0) ≥λx′(t0)f(t0,x′(t0),x′(t0),0)>0,
从而x‴(t0)>0,这与x′(t)在t=t0处达到其正的最大值以及x″(t0)=0矛盾,故式(8)成立.
于是由式(8)和边界条件(5),有
综上,不等式(6)成立.
兹断定存在t1∈(0,1),使得
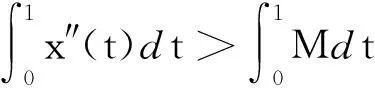
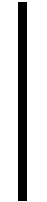
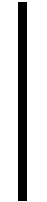
因此x″(t)在(t3,t4)内恒正或恒负.于是由假设条件(ⅲ)和N的定义,可得下面的矛盾:

故不等式(7)成立.于是由式(6)和(7),有
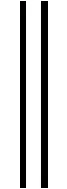
(9)
最后,我们将证明BVP(1)-(2)的解的存在性.为此,定义线性映射L:D(L)⊂C2[0,1]→C[0,1]如下:
(Lx)(t)=x‴(t),x∈D(L),
这里D(L)={x∈C3[0,1]:x(t)满足(5)},则L是一对一映射.又定义非线性映射N:C2[0,1]→C[0,1]如下:
(Nx)(t)=f(t,x(t),x′(t),x″(t)),x∈C2[0,1].
则N是有界连续映射.再定义线性映射K:C[0,1]→C2[0,1]如下:

这里G(t,s)是x‴(t)=0满足边界条件(5)的格林函数.则易见,LKx=x,∀x∈C[0,1],并且KLx=x,∀x∈D(L).更进一步,由Arzela-Ascoli定理可知,K将C[0,1]中的有界集映成C2[0,1]中的相对紧致集.因此KN:C2[0,1]→C2[0,1]是全连续的.
注意到x∈C3[0,1]是BVP(4)-(5)的解当且仅当x∈C2[0,1]是算子方程
Lx=λNx
的解.而算子方程Lx=λNx等价于算子方程
[I-λKN]x=0,
这里I:C2[0,1]→C2[0,1]是恒同映射.
degLS(I-KN,Br,0)=degLS(I-λKN,Br,0)=degLS(I,Br,0)=1.
故KN在Br内有不动点x(t).易见,此不动点x=x(t)即为BVP(1)-(2)的解,并且满足
证毕.
对于三阶四点边值问题(1)-(3),类似于定理1证明,可得如下结果:
定理2假设
(ⅰ) f(t,x0,x1,x2)∈C([0,1]×3),并且对每一个固定的(t,x1,x2)∈[0,1]×2, f关于x0单调递增;
xf(t,x,-x,0)<0;
(ⅲ) f(t,x0,x1,x2)满足Nagumo条件,即存在一个定义于[0,+)上的正值连续函数h(s),使得∀(t,x0,x1,x2)∈[0,1]×[-M,M]2×,有
则三阶四点边值问题(1)-(3)至少存在一个解x=x(t)满足
这里N与定理1中的相同.
3 例 子
考虑三阶四点边值问题
x‴=-tx3+x′ex′2+x″2, t∈[0,1],
(10)
x(0)=0, x′(0)=αx′(ξ), x′(1)=βx′(η),
(11)
这里ξ,η∈(0,1),0<α≤1,0<β≤1,并且α+β≠2.
令
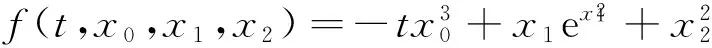
xf(t,x,x,0)=-tx4+x2ex2≥-x4+x2ex2.
而
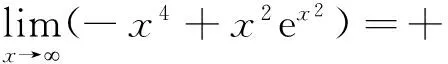
xf(t,x,x,0)>0.
此外,易见函数f(t,x0,x1,x2)满足定理1的假设条件(ⅰ)和(ⅲ).因此由定理1,三阶四点边值问题(10)-(11)至少存在一个解.
[1] H H Alsulami,S K Ntouyas,SA Al Mezel.A study of third-order single-valued and multi-valued problems with integral boundary conditions[J].Boundary Value Problems,2015,2015:25.
[2] M Gregus.Third order linear differential equations[M].Dordrecht:Reidel Publishing Co,1987.
[3] R P Agarwal.Boundary value problems for higher order differential equations[M].Singapore:World Scientific,1986.
[4] A Boucherif,N Al-Malki.Nonlinear three-point third-order boundary value problems[J].Appl Math Comput,2007,190:1168-1177.
[5] A Cabada,M R Grossinho,F M Minhós.On the solvability of some discontinuous third order nonlinear differential equations with two point boundary conditions[J].J Math Anal Appl,2003,285:174-190.
[6] C P Gupta,V Lakshmikantham.Existence and uniqueness theorems for a third-order three-point boundary value problem[J].Nonlinear Anal,1991,16:949-957.
[7] Z Du,X Lin,W Ge.On a third-order multi-point boundary value problem at resonance[J].J Math Anal Appl,2005,302:217-229.
[8] J R Graef,J Henderson,R Luca,etal.Boundary value problems for third-order Lipschitz ordinary differential equations[J].Proceedings of the Edinburgh Mathematical Society,2015,58:183-197.
[9] M R Grossinho,F M Minhós,A I Santos.Existence result for a third-order ODE with nonlinear boundary conditions in presence of a sign-type Nagumo control[J].J Math Anal Appl,2005,309:271-283.
[10] J Henderson.Best interval lengths for third order Lipschitz equations[J].SIAM J Math Anal,1987,18:293-305.
[11] B Hopkins,N Kosmatov.Third-order boundary value problems with sign-changing solutions[J].Nonlinear Anal,2007,67:126-137.[12] W Jiang,F Li.Several existence theorems of monotone positive solutions for third-order multipoint boundary value problems[J].Boundary Value Problems,2007,2007:1-9.[13] S Jin,S Lu.Existence of solutions for a third-order multipoint boundary value problem with p-Laplacian[J].Journal of the Franklin Institute,2010,347:599-606.
[14] R Ma.Multiplicity results for a third order boundary value problem at resonance[J].Nonlinear Anal,1998,32:493-499.
[15] M Pei,S K Chang.Existence and uniqueness of solutions for third-order nonlinear boundary value problems[J].J Math Anal Appl,2007,327:23-35.
[16] M Pei,S K Chang.Solvability of nth-order Lipschitz equations with nonlinear three-point boundary conditions[J].Boundary Value Problems,2014,2014:239.
[17] H Shi,M Pei,L Wang.Solvability of a third-order three-point boundary value problem on a half-line[J].Bull Malays Math Sci Soc,2015,38:909-926.
【责任编辑:陈丽华】
Existence of Solutions for Two Classes of Nonlinear Third-Order Four-Point Boundary Value Problems
Lin Donghai,Pei Minghe
(School of Mathematics and Statistics,Beihua University,Jilin 132013,China)
By using the Leray-Schauder degree theory,we obtained the existence of solutions for nonlinear third-order differentialx‴=f(t,x,x′,x″),t∈[0,1]with one of the following sets of four-point boundary conditionsx(0)=0,x′(0)=αx′(ξ),x′(1)=βx′(η);x′(0)=αx′(ξ),x(1)=0,x′(1)=βx′(η).Meanwhile,as an application of our results,an example is given.
Leray-Schauder degree theory;Nagumo condition;four-point boundary value problem;existence
1009-4822(2016)05-0572-05
10.11713/j.issn.1009-4822.2016.05.003
2016-06-15
吉林省教育厅科学技术研究项目(2016-45).
林东海(1982-),男,硕士研究生,主要从事微分方程边值问题研究,E-mail:limdonghae@163.com;通信作者:裴明鹤(1963-),男,博士,教授,主要从事微分方程定性理论研究,E-mail:peiminghe@163.com.
O175.8
A
