含时微扰论中的一个基本定理及其在分析非周期含时项的作用

陈冰瑾，刘全慧

(湖南大学 物理与微电子科学学院 理论物理研究所，湖南 长沙　410082)



含时微扰论中的一个基本定理及其在分析非周期含时项的作用

陈冰瑾，刘全慧

(湖南大学 物理与微电子科学学院 理论物理研究所，湖南 长沙410082)

文献常常在一般意义下认为含时微扰论仅仅在短时间内成立，其实是不对的，其错误在于把一些非周期时间项直接计算对概率的贡献所致.本文首先介绍了含时微扰论中的一个基本定理，进而发现很多非周期含时项，其实是相位因子的微扰展开的结果.

量子力学；含时微扰论；相因子

含时微扰论中有如下基本问题：设系统在初始时刻处在原来未扰动系统某一个能量本征态上，初始时引入微扰，问这个系统处在这个本征态上状态的改变.

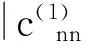
本文从基本而简单的角度讨论这个问题.发现对于一大类系统，时间的影响本质来之相位，“扰动的效果依赖于(微扰)强度和延续时间的乘积”之类的观点来自于我们在近似处理不当导致的错觉.

接下来的第1节讨论含时微扰论的一个基本定理，第2节利用该定理讨论了一个典型的二能级系统，第3节讨论和结论.

1　含时微扰论的一个基本定理

考虑含有小扰动项的哈密顿量H=H0+H′(t)，其中H0不含时间，而含时部分H′(t)为小量.零级近似哈密顿量H0可以严格处理，其本征函数集构成Hilbert空间的一组完备基：

H0φm=Emφm

(1)

含时薛定谔方程：

(2)

的解ψ(t)可以用H0给出的完备集{φm}展开：

(3)

展开系数cm(t)其实就是在H0表象中的概率幅.

薛定谔方程(2)可以改写为另外一种形式：

(4)

其中

(5)

方程(4)往往无法严格求解，需要求助于微扰近似方法.微扰近似的含义是cn(t)可以逐级展开：

(6)

(7)

这个方程的零级解即初始条件ψ(0)：

(8)

需要处理的一个典型问题是，初始时刻系统处于H0的某个定态，例如

(9)

然后再看t≥0加入微扰后系统跃迁到其他态的概率幅cm(t)(m≠n).准确到一级近似，有

(10)

此式又称为跃迁概率幅，它表示从初态φn到末态φm(m≠n)的概率幅的主要部分.

对这一典型问题，有如下基本定理.

定理：t时刻系统处于初始能量本征态φn上概率幅相位因子，其主要贡献来自第1、2级修正.

证明：

注意到态矢量的归一化条件：

1=〈ψ(t)|ψ(t)〉=

(11)

由于式(10)中的矩阵元〈n|H′|m〉中的非对角部分不可能全都为零，即cm(t) (m≠n)不可能全都为零.于是有

(12)

即

(13)

注意这个结果可以从两个角度来分析.第一，问题的出发点不是展开到二级，而是说cn(t)的主要部分一定来自二级修正.第二，从展开到二级的角度看，相位必须也要展开到二级，也就是

(14)

证毕.

下面给出两个推论.

推论一：t时刻系统处于初始定态的一级修正只可能是一个相位因子，其明显形式是

(15)

其中

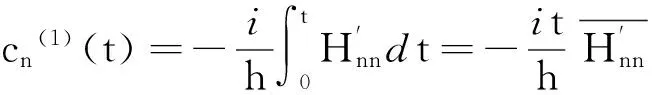
(16)

推论二：一般而言，如果在全部时间范围内总是满足

(17)

则|cn(t)|在全部时间范围内都不会发散.

这个推论看似平庸，其实极不平凡.关键是，如果全部时间范围内，式(17)成立，则cn(t)中的非周期贡献要么本质来自周期性要么是来自相因子.可参考后面[式(24)]对含时项ωt的处理.

(18)

也就是

(19)

2　对含时微扰论的一个典型问题的讨论

国内的量子力学教科书常编有如下一道习题或者其变形[4-8]，这道题目也经常出现在高校和科研院的硕博研究生的《量子力学》考题中.

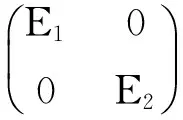
下面利用含时微扰论的标准理论计算试求t时刻系统依然处在基态上的概率，准确到第二级近似.

零级近似哈密顿量H0的本征函数可以记为

(20)

它张开了一个完备的Hilbert空间，在这个空间中，可以在任意精度上，求得这个问题的解.ω≡(E2-E1)/h.

利用微扰法，很容易得一级近似的解为

(21)

所以，系统处于激发态的概率(准确到一级近似)是

(22)

从式(19)可知，c1(t)不会出现和时间的整数幂增长的项.可是，微扰论的一般理论给出的c1(t)的二级近似是

(23)

最后得到c1(t)(准确到二级近似)

(24)

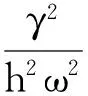
(25)

和式(19)相比较，完全符合基本定理.

下面和严格结果比较.

严格结果是[4-8]

(26)

(27)

由于只对处在基态上的二级近似感兴趣，故需要对Ω展开到二级近似：

(28)

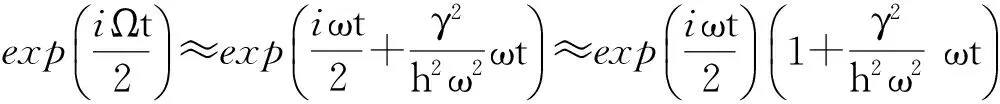
(29)

(30)

得二级近似，

(31)

(32)

3　讨论和结论

设一个系统没有简并，在初始时刻处在原来未扰动系统某一个能量本征态上，初始时引入微扰.如果微扰不大，系统在足够长的时间内跃迁到其他态的概率还是周期性的.系统会处在原来的能量本征态，和初始态的主要差别应当体现在相位因子上.

为了证明这一点，本文首先证明了一个定理，然后发现了文献中普遍忽视了非周期时间项本质来自相位，“扰动的效果依赖于(微扰)强度和延续时间的乘积”之类的观点的确来自于我们在近似处理导致的错觉.

注意到这个含时因子exp(i(γ/(hω)2ωt)其实导致了对能级的改变即重整化.这个重整化过程的一般性方法应该是微扰论中的Poincaré-Lindstedt方法.[9]在今后的研究中，我们将更深入研究这个问题.

有文献注意到含时相因子的一级修正，但是几乎没有文献注意到相因子中的二级修正.也有文献[10]分析了简并系统中，非周期时间项对概率的非周期贡献，这个问题不在本文的主题之内.

还有一些问题值得进一步研究，这些问题包括：问题更一般的讨论，周期性扰动，非简并系统等等.

[1]BallentineLE.QuantumMechanicsAModernDevelopment[M].Singapore：WorldScientific, 1998:354.

[2]Cohen-TannoudjiC,DiuBLaloeF.QuantumMechanics(Volume2)[M]，NewYork：JohnWiley，1977:1290.

[3]张永德.量子力学[M].北京：科学出版社，2006：336.

[4]曾谨言.量子力学(卷Ⅰ) [M].5版.北京：科学出版社，2013：410, 习题12.4.

[5]曾谨言.量子力学教程[M].3版.北京：科学出版社，2014：226, 习题11.3.

[6]钱伯初.量子力学[M].北京：高等教育出版社，2006：295, 习题11.3.

[7]钱伯初，曾谨言.量子力学习题精选与剖析 [M].3版.北京：科学出版社 2008：382, 习题13.4.

[8]张鹏飞，阮图南，朱栋培，等.量子力学习题指导[M].中国科技大学出版社，2009：235，习题11.3.

[9]https://en.wikipedia.org/wiki/Poincaré-Lindstedt_method

[10]SakuraiJJ,NapolitanoJ.ModernQuantumMechanics(SecondEdition) [M].NewYork：AddisonWesley, 2011:360.

Afundamentaltheoremintime-dependentquantumtheoryanditsapplicationtoanalysisofnon-periodicalterms

CHENBing-jin，LIUQuan-hui

(InstituteofTheoreticalPhysics,SchoolofPhysicsandMicroelectronicScience,HunanUniversity,Changsha,Hunan410082,China)

Textbooksonquantummechanicsusuallyassertthatperturbationtheoryholdstrueonlyforsufficientshorttime.Thismistakeresultsfromdirectcontributionofthenon-periodicaltimetermintoprobabilities.Wefirstintroduceafundamentaltheoreminthetime-dependentquantumtheory,thenpointoutthatthenon-periodicaltimetermsareinfactperturbationexpansionsoftime-dependentphasefactor.

quantummechanics;time-dependentquantumtheory;phasefactor

2015-11-16；

2016-01-30

国家自然科学基金资助课题(11175063)；湖南大学教改基金资助课题

陈冰瑾(1992—)，女，山东青岛人，电子科学与技术学士，湖南大学理论物理研究所研究助理.

O413.1

A

1000- 0712(2016)08- 0014- 04