一维氢原子模型中的空间分离

王　鑫，刘天贵，刘全慧

(湖南大学 物理与微电子科学学院 理论物理研究所，湖南 长沙410082)



一维氢原子模型中的空间分离

王鑫，刘天贵，刘全慧

(湖南大学 物理与微电子科学学院 理论物理研究所，湖南 长沙410082)

一维氢原子模型原始的定义在全空间x∈(-∞,∞)，多年的研究发现，由于势～-1/|x|的奇异性比想象严重，空间被分割成为了两个独立的半无限空间.在这两个独立的空间中，分别定义了两个半空间中的氢原子.

一维氢原子模型；空间分离；奇异势能

1　一维氢原子模型，通常教科书中“标准”处理及其结果

一维氢原子模型指的是一个负电荷(-q)在一个质量无限大的正电荷Q中的运动，最简单的情况是Q=q=e为电子电荷的绝对值.电势能为

(1)

其中k=qQ/(4πε0)→e2/(4πε0)为一正常数，|x|为正负电荷间的距离.在量子力学中，哈密顿算符为

(2)

定态薛定谔方程为

Hψ=Eψ

(3)

物理学界第一次注意到这个问题是1952年[1]，后来又反复回到这一问题.2009年的一篇《论一维库仑问题》[2]的短文，列出了54篇相关文献，而这篇论文现有15篇引用(2015年10月3日google数据).当然，这些论文不全是、也不可能是这个问题的全部研究论文.对这个问题的研究兴趣持续不减，至今(2015年)仍是[3,4]，既有理论上的原因，例如它涉及到很现代的概念例如超对称[2]、重整化[5]等；也由于多种物理问题可以用相互作用进行近似处理，详情可参见文献[2]中的综述部分.

从教学研究的角度看，对于一维体系，有3个相关的定理.定理之一是：基态无简并且没有节点.定理之二是：粒子在对称势场中运动，那么对于某一能级的定态，如果没有简并，则该态具有确定的宇称.定理之三是：粒子在充分规则的势场中运动，如果有束缚态，则必定不是简并的.

由于一维氢原子模型的势能在x=0处奇异，故不满足定理三；由于定理二处理的是一般情况，本质上也要求势函数充分规则，所以定理二也不适用.只剩下定理一，似乎不能不满足，但是问题远比预期复杂.

从表面上看，方程(3)的解可以通过如下过程而获得.

1) 对于非奇异态，波函数本身及其导数连续，故ψ(0)=0. 证明如下.

现在处理的是全一维空间x∈(-∞,∞)，而x=0是势能V(x)的奇点，也就是系统哈密顿算符的奇点，这一点的态只能由边值关系来确定.对式(3)的两边同时积分，得

(4)

第二个积分是一个广义积分，需要研究其积分主值

(5)

这个积分有意义要求满足条件：

ψ(0-)+ψ(0+)=0

(6)

另一方面，波函数本身必须连续，即

ψ(0-)=ψ(0+)=ψ(0)

(7)

故得

ψ(0)=0

(8)

证毕.

2) 基态可能是奇异态，可以利用各种渐近过程去逼近这个奇异态.一种方式就是利用如下势能：

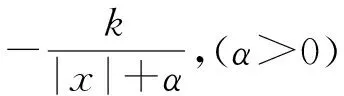
(9)

先求出基态，然后让参量α→0，或者β→0，发现可能存在一个奇异态：

(10)

这个态对应的能量为负无穷大，即

E0=-∞

(11)

3) 哈密顿算符(2)具有一个明显的性质：宇称算符P和哈密顿H对易，即

[H,P]=0

(12)

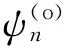
(13)

(14)

它们构成二重简并态，对应的能量本征值为

(15)

也就是通常的氢原子能级.

2　“标准”结果中的一些数学上的困难

1) 数学上，哈密顿算符(2)不是一个自伴算符[4,5].这个算符从形式上看，是如下算符的极限：

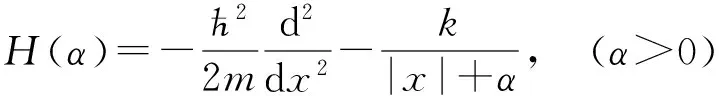
(16)

这两个算符是自伴算符！但是，H(α→0)≠H(α=0)，也就是自伴算符的极限完全可以是非自伴算符.如何理解这个“怪异”的现象呢?

一般来说，数学上，极限有3种情况.下面用定义在一个圆域r∈[0,1)内的函数f(r)的数值和它在边界r=1点处函数值f(1)之间的关系来说明.第一种情况最简单，f(1)极限存在，而这点的极限数值可以通过逼近来获得，有

f(1)=f(0.999…)

(17)

第二情况是，f(1)极限存在，而这点的极限数值不可以通过逼近来获得，即

f(1)≠f(0.999…)

(18)

一个半径为1的圆形的筛子，就属于这种情况.注意这个筛子是一个理想的数学抽象，边沿不连续地直立向上而底面是圆面，这个边沿的厚度为零.

第三情况是，r=1根本没有定义，谈论这点的极限数值无意义.一个例子是上面的圆形筛子把边齐根剪掉之后的情况.

很明显，我们碰到一个极为容易忽视的问题，表面上看来，式(2)是式(15)的极限，也就是属于上面的第一种情况，其实不是！当a=β=0时，算符不是自伴算符，根本不属于自伴算符族H(α)或者H(β)中a→0或者β→0的极限情况.故属于第二种情况式(18).

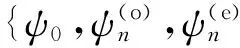
(19)

也就是有

ψ′(0+)-ψ′(0-)=0

(20)

而把式(14)代入后发现[6,7]：

ψ′(0+)-ψ′(0-)≠0

(21)

故而应该剔除偶宇称解.

以上3点，不是数学困难的全部，有些问题超出了大学物理的范围，例如来自超选择规则(superselection rule)[6]，超对称势伴(supersymmetric partner)势[6]，等等，可以参看有关专业文献.

3　“标准”结果中的一些物理上的困难

1) 任何波包都不随时间演化.任意构造一个波包：

(22)

直接计算可得它不仅概率流密度为零，而且位置和动量的期待值为零：

j(0)=0,〈x〉=0,〈p〉=0

(23)

这个结果暗示，从这个系统中读不出任何信息.要么这是一个完全非物理的模型；要么它是一个物理的模型，但我们可能忽视了某个重要的原则.

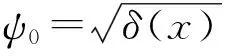
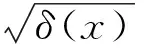
(24)

把这个结果延拓到E<0(复γ)能域，T的简单极点对应的束缚态能量正好是E=-μγ2/(2ћ2).

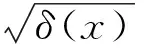
3) 一个不是很严重的困难是基态解的负无穷能量问题.任何高能级上的粒子会由于自发跃迁而向基态跃迁，如果这样，系统将一直呆在基态上.反过来，如果粒子已经在基态上，似乎就无法跃迁到激发态去.不过，自发跃迁要求有物理真空的存在，而对一维系统如何定义这一真空，且这一真空是否可导致通常的自发跃迁不是很清楚；反过来，如果存在一维真空，而真空中有无限大的能量，这个能量足够把基态上的粒子激发出来.

4) 另外一个不是很严重的困难是，这个问题没有经典对应.在经典力学中，这个问题的解认为粒子只能分别局限在两个半空间中运动，而不能从左半空间运动到右半空间去.为什么这个困难也不是很严重? 这是因为，经典力学中不存在的东西，量子力学中可以存在.

4　“标准”结果的数学和物理的困难导致必须正确理解一维氢原子模型

定义在一维全空间x∈(-∞,∞)中的一维氢原子模型，有许多困难，但是根本的困难在于x=0时，势的奇异性太厉害，以至于把空间分割成为了两个独立的半无限空间.这样，一维氢原子模型变得异常简单，

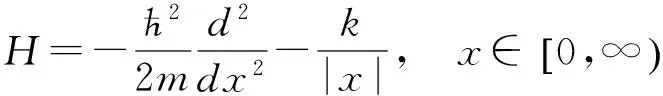
(25)

这个系统的能量就是氢原子能级式(15)，定态为φn(x),(x>0)或者φn(-x),(x<0).它本质上就是三维氢原子中零角动量的解.

如果考虑到核半径的有限性，一维氢原子模型的势能最好由式(9)来描述，这个时候，奇宇称和偶宇称的解同时存在，但是不简并[10].关于一维体系的许多量子力学定理都平庸地适用.

5　结论和讨论

尽管形式一样，二维、三维空间中库仑势-1/r的奇异性和一维势-1/|x|的奇异性完全不同.一维氢原子模型不能定义在全空间x∈(-∞,∞)，由于势的奇异性太严重，以至于x=0处，空间被分割成为了两个独立的半无限空间.每个半空间中都有一个一维氢原子.

对于奇异系统，不是一些已知的定理能不能用的问题，而是根本不在同一框架中.这说明在物理学中，每碰到特异性时，往往需要单独研究.

[1]Flügge S,Marschall H.Rechenmethoden der Quantentheorie [M].Berlin: Springer-Verlag,1952:69.

[2]Benjamín Jaramilloa,Martínez-y-Romerob R P,Núez-Yépezc H N,et al. On the one-dimensional Coulomb problem[J]，Phys Lett A，2009,374(2):150-153.

[3]Carrillo-Bernal M A,Núez-Yépez H N,Salas-Brito A L,et al. Comment on “Calculations for the one-dimensional soft Coulomb problem and the hard Coulomb limit” [J].Phys Rev E,2015,91: 027301.

[4]Daniel H Gebremedhin,Charles A Weatherford.Calculations for the one-dimensional soft Coulomb problem and the hard Coulomb limit [J].Phys Rev E,2014，89:053319；Reply to “Comment on ‘Calculations for the one-dimensional soft Coulomb problem and the hard Coulomb limit’ ” [J].Phys Rev E,2015,91: 027302.

[5]Mineev V S.The Physics of Self-Adjoint Extensions: One-Dimensional Scattering Problem for the Coulomb Potential [J].Teoret Mat Fiz,2004,140(2): 310-328.

[7]Dai Xianxi，Dai Jixin，Dai Jiqiong.Orthogonality criteria for singular states and the nonexistence of stationary states with even parity for the one-dimensional hydrogen atom [J].Phys Rev A,1997,55: 2617.

[8] Oseguera U,de Llano M.Two singular potentials: The space-splitting effect [J].J Math Phys,1993,34: 4575.

[9]曾谨言.量子力学(卷I)[M].5版.北京：科学出版社，2013：91；240.

[10]Daniel H Gebremedhin，Charles A Weatherford.Calculations for the one-dimensional soft Coulomb problem and the hard Coulomb limit [J].Phys Rev E，2014,89: 053319.

Space-splitting in the one-dimensional hydrogen atom model

WANG Xin，LIU Tian-gui,LIU Quan-hui

(School for Theoretical Physics,School of Physics and Microelectronic Science,Hunan University,Changsha,Hunan 410082,China)

The potential energy for one-dimensional hydrogen atom is usually modelled by-1/|x|over the entire spacex∈(-∞,∞).Studies over years reach a consensus that the space is separated into two impermeably semi-infinite spaces due to the serious singularity of the potential.In the two spaces, there exist two independent one-dimensional hydrogen atoms.

one-dimensional hydrogen atom;space-splitting;singular potential

2015-08-00；

2015-10-08

国家自然科学基金资助课题(批准号：11175063)；湖南大学教改基金资助课题.

王鑫(1966-)，女，河南舞阳人，湖南大学物电院副教授，博士.

O 413.1

A

1000- 0712(2016)03- 0030- 04