基于ANSYS Workbench的面齿轮传动固有特性分析
2016-10-15王其雷何国旗邓澍杰
王其雷,何 瑛,何国旗,邓澍杰,孙 能
(1. 湖南工业大学 机械工程学院,湖南 株洲 412007;2. 湖南理工职业技术学院 资源工程系,湖南 湘潭 411104)
基于ANSYS Workbench的面齿轮传动固有特性分析
王其雷1,何瑛2,何国旗1,邓澍杰1,孙能1
(1. 湖南工业大学 机械工程学院,湖南 株洲 412007;2. 湖南理工职业技术学院 资源工程系,湖南 湘潭 411104)
以正交面齿轮传动为研究对象,建立面齿轮传动的有限元模型,运用有限元软件ANSYS Workbenck对该模型进行模态分析,提取该模型的前6阶固有频率和振型进行分析;并研究压力角、齿数差及面齿轮孔径对面齿轮传动固有频率的影响。研究结果表明:面齿轮传动的模态振型以面齿轮振动为主,面齿轮传动固有频率随压力角、齿数差及面齿轮孔径的增大而增大,其中面齿轮孔径对其影响最大,其次是压力角,而齿数差对其影响不大。
面齿轮;ANSYS Workbench;模态分析;固有频率;振型
0 引言
面齿轮传动是一种新型的齿轮传动形式,具有重合度高、噪声低、振动小等许多优点[1-3]。随着科技的不断发展,面齿轮传动因其独特的分流特性,使其在新型战斗直升机主减速器系统中已逐渐得到应用。齿轮传动时,内外部激励会使系统产生机械振动,振动系统的固有特性对系统的动态响应、振动形式以及动载荷的产生与传递等都有重要影响[4]。齿轮传动的固有特性研究是齿轮结构动态设计及故障诊断的重要方法[5-6]。
目前,对于圆柱齿轮和锥齿轮传动固有特性的分析,已有较多的学者进行了研究[7-10];而对于新型的面齿轮传动,相关研究文献较少,张乐等[11]建立了面齿轮传动分扭系统的动力学模型,分析了啮合刚度对系统固有频率的影响。
本文以正交面齿轮传动为研究对象,根据面齿轮切齿啮合关系和空间啮合原理,推导出正交面齿轮齿面方程,运用MATLAB和Pro/E软件建立面齿轮传动三维实体模型,基于ANSYS Workbench软件对该模型进行模态分析,提取该模型的前6阶固有频率和振型进行分析,并研究压力角、齿数差及面齿轮孔径对面齿轮传动固有频率的影响。
1 面齿轮传动系统微分方程
设面齿轮传动系统为具有n个自由度的线弹性振动系统,其运动微分方程[12]为
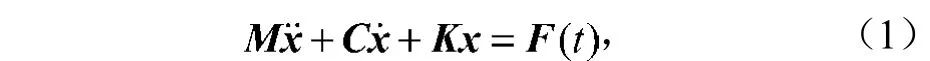
式中:M为质量矩阵;C为阻尼矩阵;K为刚度矩阵;F(t)为力矢量;x为位移矢量;为速度矢量;为加速度矢量。
在模态分析中,不考虑阻尼和外力作用,该系统无阻尼运动方程为
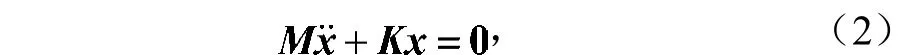
一般假设系统结构的自由振动为简谐振动,即位移为正弦函数,则方程(2)化简为
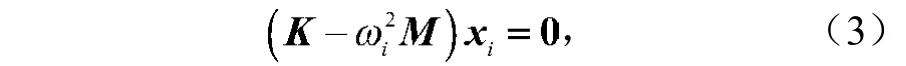
式中:xi为第i阶模态的主振型;
因此,模态分析中系统的固有频率和振型由系统的质量和刚度确定。
求解面齿轮传动系统微分方程,一般采用振型叠加法或逐步积分法,运用有限元软件ANSYS Workbench可以实现繁琐的求解过程,操作简单、计算时间短且计算稳定。
2 基于Workbench的模态分析
2.1几何模型的建立
由于面齿轮齿面结构比较复杂,为得到精确的面齿轮几何模型,根据范成原理,利用刀具插齿加工得到面齿轮,所用刀具的尺寸与实际啮合的渐开线圆柱齿轮相同或相近,具体插齿加工坐标系如图1所示。图中:zf0(zf)与zs0(zs)分别为面齿轮与刀具的旋转轴,坐标原点为两轴线的交点;坐标系Sf0-Of0xf0yf0zf0与Sf-Ofxfyfzf分别为面齿轮的固定与转动坐标系,Ss0-Os0xs0ys0zs0与Ss-Osxsyszs分别为刀具的固定与转动坐标系。f与s分别为加工中面齿轮和刀具转过的角度。
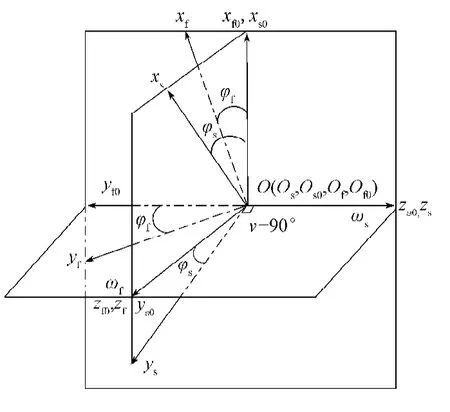
图1 正交面齿轮插齿加工坐标系示意图Fig. 1 The schematic for coordinate system of orthogonal face-gear shaping machining
根据面齿轮切齿啮合关系和空间啮合原理,借助矩阵法推出面齿轮齿面方程[13]为
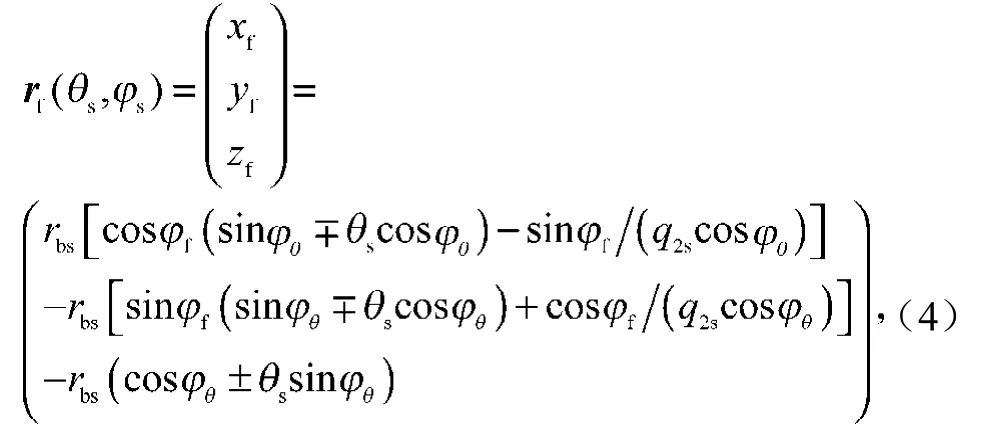
式中:rbs为刀具渐开线的基圆半径;
q2s=Nf/Ns,其中Nf为面齿轮的齿数,Ns为刀具齿数。
应用MATLAB软件求解面齿轮齿面方程(4)的离散点三维坐标数据,通过Pro/E软件进行重构,获得面齿轮三维实体模型。
标准渐开线直齿圆柱齿轮采用Pro/E参数化建模,所建圆柱齿轮一般比刀具齿数少1~3个[14],并对面齿轮和圆柱齿轮进行啮合装配。面齿轮传动模型主要参数:面齿轮齿数1=80,圆柱齿轮齿数2=22,模数m=5,齿宽b=40 mm,压力角 =20°,面齿轮孔径d1=90 mm,圆柱齿轮孔径d2=40 mm,面齿轮轮毂厚度T=20 mm,如图2所示。

图2 面齿轮传动三维实体模型Fig. 2 The 3D model of face-gear drive
2.2有限元模型的建立
利用Pro/E与ANSYS Workbench软件接口将三维实体模型导入到ANSYS Workbench中,建立有限元模型需要进行以下设置。
1)定义材料属性:弹性模量E=2.06×1011Pa,泊松比=0.3,密度=7 850 kg/m3。
2)创建接触:对于一对啮合轮齿,需要建立2个齿轮之间的接触关系,采用面面接触单元定义接触齿面,修改接触类型Bonded为Frictionless。
3)网络划分:选择智能网络划分,面齿轮采用四面体单元,圆柱齿轮采用六面体单元,划分后Node数为52 106,Elements数为20 625,如图3所示。
4)加载约束:面齿轮设置绕 轴的旋转自由度,其余自由度固定;圆柱齿轮设置绕x轴的旋转自由度,其余自由度固定。由于是模态分析,因此无需添加外载荷。
图3 面齿轮传动有限元模型Fig. 3 The finite element model of face-gear drive
2.3模态分析与计算
考虑到模型规模和实际硬件条件,本模型的模态计算选择了迭代求解器Iterative的求解方法,计算模型的6阶模态,提取模型的前6阶固有频率与振型,如表1和图4所示。

表1 面齿轮传动固有频率Table 1 The natural frequency of face-gear drive

图4 面齿轮传动模态振型Fig. 4 The modal shapes of face-gear drive
由表1和图4可以看出:面齿轮传动模型的前6阶固有频率主要分布范围为310~1 100 Hz,对应的振型以面齿轮振动为主。第1阶模态振型为绕y轴的左右摆动,第2阶模态振型为绕x轴的前后摆动,第3阶模态振型为绕y轴的弯曲变形,第4阶模态振型为绕x轴的扭转变形,第5阶模态振型为绕y轴的弯曲、扭转组合变形,第6阶模态振型为绕x轴的弯曲、扭转组合变形。
根据上述分析,当面齿轮传动的工作频率与其某阶模态振型接近时,就需要在设计时采取措施避免对应的部位可能出现破坏。比如面齿轮传动的工作频率及啮合频率要避开其各阶固有频率,以防止在运行中发生共振现象,导致机器故障,并造成一定的经济损失。
3 设计参数对固有频率的影响
为验证面齿轮压力角 、圆柱齿轮与刀具的齿数差d及面齿轮孔径d1对面齿轮传动固有频率的影响,取面齿轮齿数1=80,刀具齿数3=25,模数m=5,齿宽b=40 mm,圆柱齿轮孔径d2=40 mm,面齿轮轮毂厚度T=20 mm;以压力角、圆柱齿轮齿数、面齿轮孔径等设计参数分别作为单一变量进行分析,如表2所示。

表2 面齿轮传动参数变化Table 2 The parameter variation of face-gear drive
根据表2中第1组参数,分别得出不同压力角的面齿轮传动固有频率,如表3所示。
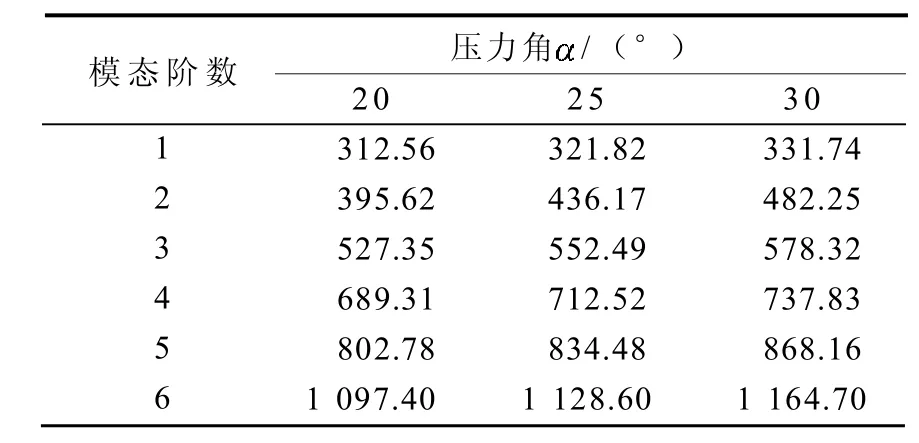
表3 不同压力角的面齿轮传动固有频率Table 3 The natural frequency of face gear drive with different pressure angles
由表3中的数据可知:随着压力角增大,面齿轮传动固有频率也增大,其中1阶模态频率增幅最小,2阶模态频率增幅最大。
根据表2中的第2组参数,分别得出不同孔径的面齿轮传动固有频率,如表4所示。
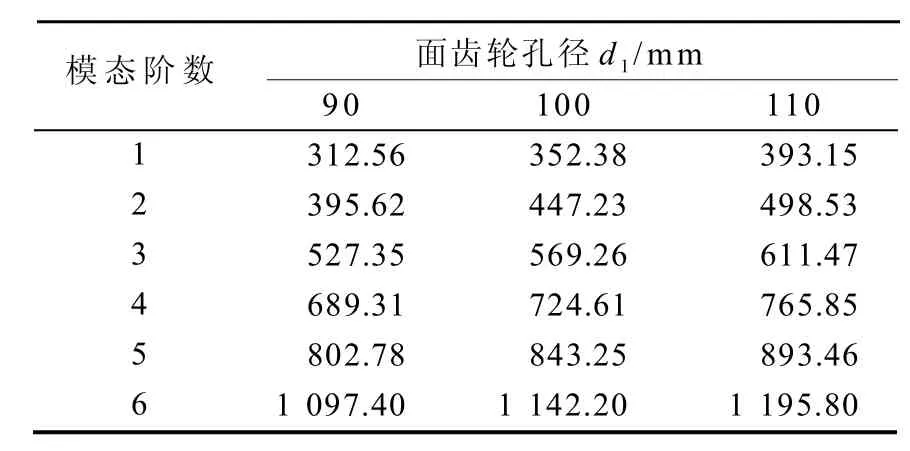
表4 不同孔径的面齿轮传动固有频率Table 4 The natural frequency of face gear drive with different apertures
由表4中的数据可知:随着面齿轮孔径增大,面齿轮传动固有频率增大。对比表3和表4可知:孔径变化比压力角变化对面齿轮传动固有频率的影响更大。
根据表2中的第3组参数,分别得出不同齿数差的面齿轮传动固有频率,如表5所示,其中齿数差分别为3, 2, 1时,对应的圆柱齿轮齿数分别为22, 23, 24。
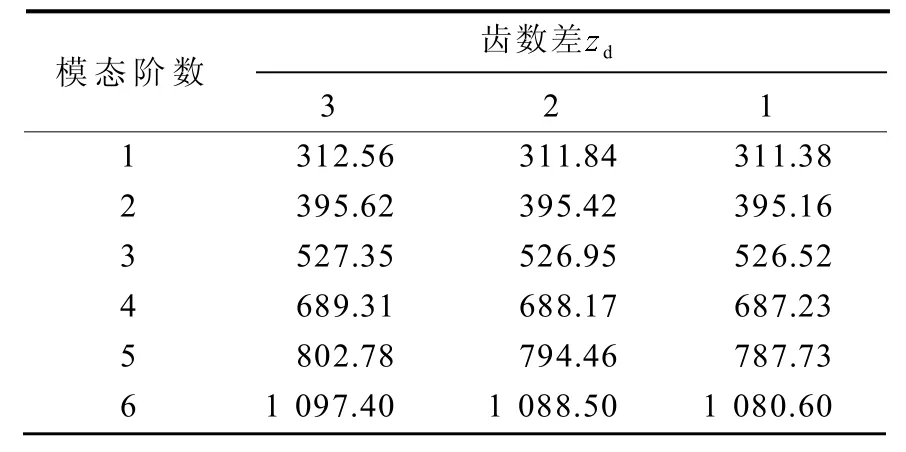
表5 不同齿数差的面齿轮传动固有频率Table 5 The natural frequency of face gear drive with different tooth number difference
由表5中数据可知:随着齿数差增大,面齿轮传动固有频率略有提高,其中低阶(1~4阶)模态频率几乎没有变化,高阶(5~6阶)模态频率有较小程度增幅,这说明齿数差对面齿轮传动固有频率影响不大。
4 结语
本文建立了面齿轮传动模型,运用有限元分析软件ANSYS Workbench对模型进行模态分析,得出模型的前6阶固有频率与振型。为避免传动过程中发生共振现象,应使激励响应的频率避开固有频率。研究了压力角、面齿轮孔径及齿数差对面齿轮传动固有频率的影响,并得出了相应的规律:面齿轮传动固有频率随压力角、齿数差及面齿轮孔径的增大而增大,其中孔径变化对其影响最大,其次是压力角,而齿数差对其影响不大。此结论可为面齿轮传动的优化设计提供理论参考。
[1]HANDSCHUH R,LEWICKI D,BOSSLER R. Experimental Testing of Prototype Face-Gears for Helicopter Transmissions[R]. Solihull:NASA Technical Memorandum 105434,1992:1-10.
[2]LITVIN F L,CHEN N X,CHEN J S. Computerized Determination of Curvature Relations and Contact Ellipse for Conjugate Surfaces[J]. Computer Methods in Applied Mechanics and Engineering,1995,125(1):151-170.
[3]LITVIN F L,ZHANG Y,WANG J C,et al. Design and Geometry of Face-Gear Drives[J]. Journal of Mechanical Design,1992,114(4):642-647.
[4]万凯宇. 行星齿轮传动系统动力学分析研究[D]. 南京:南京航天航空大学,2004. WAN Kaiyu. Research on Dynamic Analysis of Epicyclic Gear Drive System[J]. Nanjing:Nanjing University of Aeronautics and Astronautics,2004.
[5]张振峰,王筱,王帅,等. 基于ABAQUS的减速器齿轮的模态分析[J]. CAD/CAM与制造业信息化,2010(12):62-64. ZHANG Zhenfeng,WANG Xiao,WANG Shuai,et al. Modal Analysis of Gear Reducer Based on ABAQUS[J]. Intelligent Manufacturing,2010(12):62-64.
[6]王春光. 行星齿轮传动动态特性的研究[D]. 北京:中国舰船研究院,2005. WANG Chunguang. Investigation of Dynamic Characteristic of Planetary Gear Transmission[D]. Beijing:China Ship Research and Development Academy,2005.
[7]沈允文,邵忍平. 齿轮结构振动固有特性研究[J]. 机械强度,2000,22(1):12-15. SHEN Yunwen,SHAO Renping. Study of Natural Characteristic for Structural Vibration of Gears[J]. Journal of Mechanical Strength,2000,22(1):12-15.
[8]吴文光,朱如鹏. 基于Workbench的斜齿轮固有特性分析[J]. 机械传动,2010,34(4):54-56. WU Wenguang,ZHU Rupeng. Analysis on Natural Vibration Characteristics of Helical Gear Based on Workbench[J]. Journal of Mechanical Transmission, 2010,34(4):54-56.
[9]任海果,吴斌. 弧齿锥齿轮固有振动特性分析[J]. 机械设计与制造,2012(2):51-53. REN Haiguo,WU Bin. Analysis for Natural Vibration Characteristics of Spiral Bevel Gears[J]. Machinery Design & Manufacture,2012(2):51-53.
[10]王佳威. 船用大型齿轮传动的振动分析和动力学研究[D].武汉:武汉理工大学,2012. WANG Jiawei. An Analysis of Gear Transmission Vibration & Dynamic Study of Marine Gear[D]. Wuhan:Wuhan University of Technology,2012.
[11]张乐,朱如鹏,李政民卿. 面齿轮传动分扭系统扭转振动的固有频率分析[J]. 机械制造与自动化,2012,41(5):21-24. ZHANG Le,ZHU Rupeng,LI ZHENG Minqing. Research on Natural Frequency of Torsional Vibration of Torque-Split Face Gear Transmission System[J]. Machine Building & Automation,2012,41(5):21-24.
[12]师汉民. 机械振动系统:上册[M]. 武汉:华中科技大学出版社,2004:154-164. SHI Hanmin. Mechanical Vibrating System:Part 1[M]. Wuhan:Huazhong University of Science and Technology Press,2004:154-164.
[13]舒陶亮,何国旗,孙晓,等. 面齿轮啮合过程中齿面接触应力分布研究[J]. 湖南工业大学学报,2012,26(3):52-57. SHU Taoliang,HE Guoqi,SUN Xiao,et al. Research on the Distribution of Face-Gear Tooth Surface Contact Stress in Meshing Process[J]. Journal of Hunan University of Technology,2012,26(3):52-57.
[14]唐进元,刘艳平. 直齿面齿轮加载啮合有限元仿真分析[J]. 机械工程学报,2012,48(5):124-131. TANG Jinyuan,LIU Yanping. Loaded Meshing Simulation of Face-Gear Drive with Spur Involute Pinion Based on Finite Element Analysis[J]. Journal of Mechanical Engineering,2012,48(5):124-131.
(责任编辑:邓光辉)
Analysis on Natural Vibration Characteristics of Face-Gear Drive Based on ANSYS Workbench
WANG Qilei1,HE Ying2,HE Guoqi1,DENG Shujie1,SUN Neng1
(1. School of Mechanical Engineering,Hunan University of Technology,Zhuzhou Hunan 412007, China;2. Department of Resources Engineering,Hunan Vocational Institute of Technology,Xiangtan Hunan 411104,China)
With orthogonal face-gear drive as the research object, a finite element model of face-gear drive is established. The FEA software of ANSYS Workbenck is used to analyze the model and the first 6 natural frequencies and mode shapes of the model are extracted. The influences of pressure angle, tooth number difference and face-gear aperture on the natural frequency of face-gear drive is studied. The results show that the modal vibration mode of the face-gear drive is mainly based on face-gear vibration, the natural frequency of face-gear drive increases with the increment of pressure angle, tooth number difference and face-gear aperture. In these factors, the impact of face-gear aperture is the greatest, followed by pressure angle, and tooth number difference has little effect.
face-gear drive;ANSYS Workbench;modal analysis;natural frequency;vibration mode
TH132.41
A
1673-9833(2016)01-0001-05
10.3969/j.issn.1673-9833.2016.01.001
2015-12-03
国家自然科学基金资助项目(51375159),湖南省自然科学株洲联合基金资助项目(2015JJ5020),湖南省高等学校科学研究基金资助项目(12A038,13C379)
王其雷(1989-),男,山东济南人,湖南工业大学硕士生,主要研究方向为机械设计与制造,E-mail:58657408@qq.com
何瑛(1969-),女,湖南湘潭人,湖南理工职业技术学院高级工程师,主要从事数字化制造理论与技术方面的教学与研究,E-mail:503904249@qq.com
