基于DOE与MPI的注塑成型工艺稳健优化设计

林权

（武夷学院 机电工程学院，福建 武夷山 354300）

基于DOE与MPI的注塑成型工艺稳健优化设计

林权

（武夷学院 机电工程学院，福建 武夷山 354300）

翘曲变形量是评价卡扣塑料平板装配质量合格性的重要指标。应用田口正交试验法（DOE），结合模流工程分析模块（MPI），对制品进行翘曲变形研究。通过对注塑成型工艺参数进行稳健优化设计，经过试验分析获取最优工艺参数组合，并利用置信区间计算验证了最优参数组合的可靠性。研究结果表明：保压时间为最显著的影响因子，其次为冷却时间、塑料温度以及保压压力；保压时间和冷却时间较长易造成制品内应力增加，有导致翘曲变形的可能性。

翘曲变形；田口正交试验；Moldflow；稳健优化

0　引言

在注射成型中，影响制品翘曲变形的因素很多，主要与注塑模具浇注系统设计、冷却系统设计以及成型工艺参数设计密切相关［1］。随着人们环保意识的加强，现代塑料制品设计越来越精巧化，薄壁设计也越来越多。但是薄件塑料产品不仅需要更大的注射压力，而且容易引起翘曲变形，尤其是薄件平板类塑料制品［2-4］。

卡扣塑料平板是连接装配件，翘曲变形量是评价卡扣塑料平板装配质量合格性的重要指标。本文基于田口正交试验法（DOE），结合Moldflow 模流工程分析软件，通过对注塑工艺参数进行稳健优化设计及系统试验分析，探讨注射成型工艺条件对制品翘曲变形的影响，进而求得最小翘曲量的注射成型参数组合，最终使制品获得较高的几何形状精度，以提高制品质量，降低其研发成本。

1　创建分析模型与材料选择

在进行模型分析之前，必须创建网格模型［5］。首先应用Solidworks 创建卡扣塑料平板制品的3D模型，再导入模流工程分析模块（Moldflow plastics insight，MPI），使用双层面网格对模型进行网格划分与修改，将纵横比修复至6 以下，配向和交叉元素个数都为0，且匹配率达到95%以上，才可以进行流动+保压+翘曲分析。最后通过浇注系统设计和创建冷却系统建立的卡扣塑料平板有限元分析模型如图1所示。图中制品外观尺寸长为260 mm，宽为104 mm，平均厚度约为2 mm。制品上表面中心线上均匀分布3个卡扣，下表面左右对称4个角均匀分布4个卡扣。浇注系统采用梯形分流道，分流道顶部宽度为5 mm，底部宽度为4 mm，厚度为4 mm。系统为四点点浇口进料，浇口形状为椎体，始端直径为2 mm，锥体角度为2°。冷却系统为直流循环式，冷却水道直径为8 mm，平行等距分布于制品上下表面，距离约为25 mm。

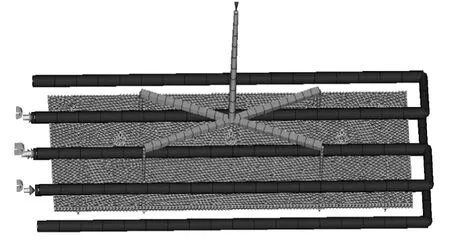
图1　卡扣塑料平板有限元分析模型Fig. 1　Finite element analytical model for snap-in plastic plates

试验材料为台湾奇美实业股份有限公司生产的丙烯腈-丁二烯-苯乙烯共聚物（acrylonitrile butadiene styrene，ABS），牌号为一般注塑级Polylac PA-757。材料呈浅象牙色，外形为粒状或珠状，210 ℃即可达到材料的熔融温度，250 ℃即可达到材料的降解温度。ABS树脂具有优良的力学性能，故而在电子仪器仪表、汽车制造、建材工业等领域得到了广泛应用［6］。依据实际经验，ABS材料成型参数选取恒模温度为80 ℃，熔料温度为210～250 ℃，注射压力为80～150 MPa，由于保压时间相对较短，保压压力可取注射压力的50%～80%。

2　田口试验设计与优化

田口试验设计方法的特点是：设计的产品质量稳定，波动性小，且生产过程对各种噪声不敏感［7-8］。田口方法是依照控制因子及水平数选择适当的直交表，并以信噪比（signal to noise，S/N）作为试验数据的来源，再讨论选择的控制因子对指标特性影响的显著性。

2.1确定制品质量指标

理想的注射产品尺寸形状精度与模具型腔型芯尺寸是一致的，也就没有变形翘曲或者缩水等现象；但实际上，由于模具各个部分温度不一致导致制品各个方向收缩不均，常存在翘曲现象［9-11］。本制品也不例外，卡扣塑料平板为连接装配件，翘曲变形程度对其合格性影响较大，且为望小特性，即非负数值且其值越小越好的特性，因此翘曲变形量为本制品的质量特性指标。

2.2选定控制因子与水平

因子又称为自变量，也就是在成型过程中会影响质量特性的参数，因子可分为控制因子、信号因子和干扰因子［8］。控制因子是在设计或制造上选取用以改善质量目标稳健性的因子，是设计人员可以掌控与决定的参数。信号因子是评价S/N 比值信号的因子，设计者可以通过调整信号因子，从而改变产品质量特性值。干扰因子是指由于内部、外部等所有造成变异的原因。

选定控制因子为：塑料温度（℃）、充填时间（s）、保压时间（s）、冷却时间（s）、开模时间（s）、注射压力（MPa）、保压压力（MPa）。除了塑料温度取2个水平，其他分别赋予3水平，控制因子水平如表1所示，表中相关参数为实际现场依照经验法则测试而定，其中保压压力分别选取注射压力的60%，70%和80%，因子A～G的工艺参数可以根据实际需求进行合理选择。

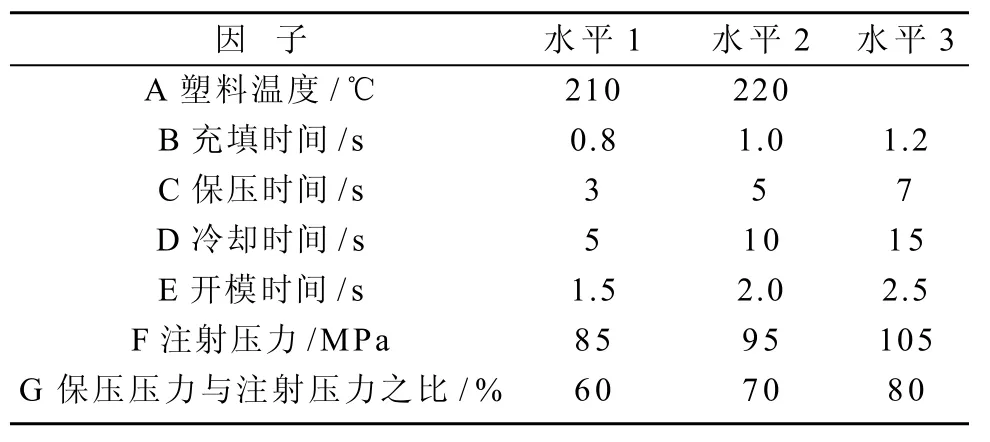
表1　控制因子及水平Table 1　Controlling factors and levels

2.3选定直交表

田口试验直交表可利用较少试验次数求得所需结果，并且试验获得的结论在整个试验范围内都是成立的，通过各因子计算简单的平均值，又可获知每个控制因子的效果［10］。直交表中任2行内积为0，各因子水平出现次数均相同。直交表的使用方式有2种，一种为使用单纯直交表，根据表内配置组合进行试验，需重复试验获得客观数值；如果遇到不可控制的干扰因素时，就必须使用另一种方式，使用两直交表的组合，控制因子放置于内侧直交表，而干扰因子放置于外侧直交表。在此选定7 个控制因子、3 水平数且不考虑交互作用，采用田口试验法所推荐的L18（21×37）表，根据表1所设计出原始成型参数试验数据，如表2所示。

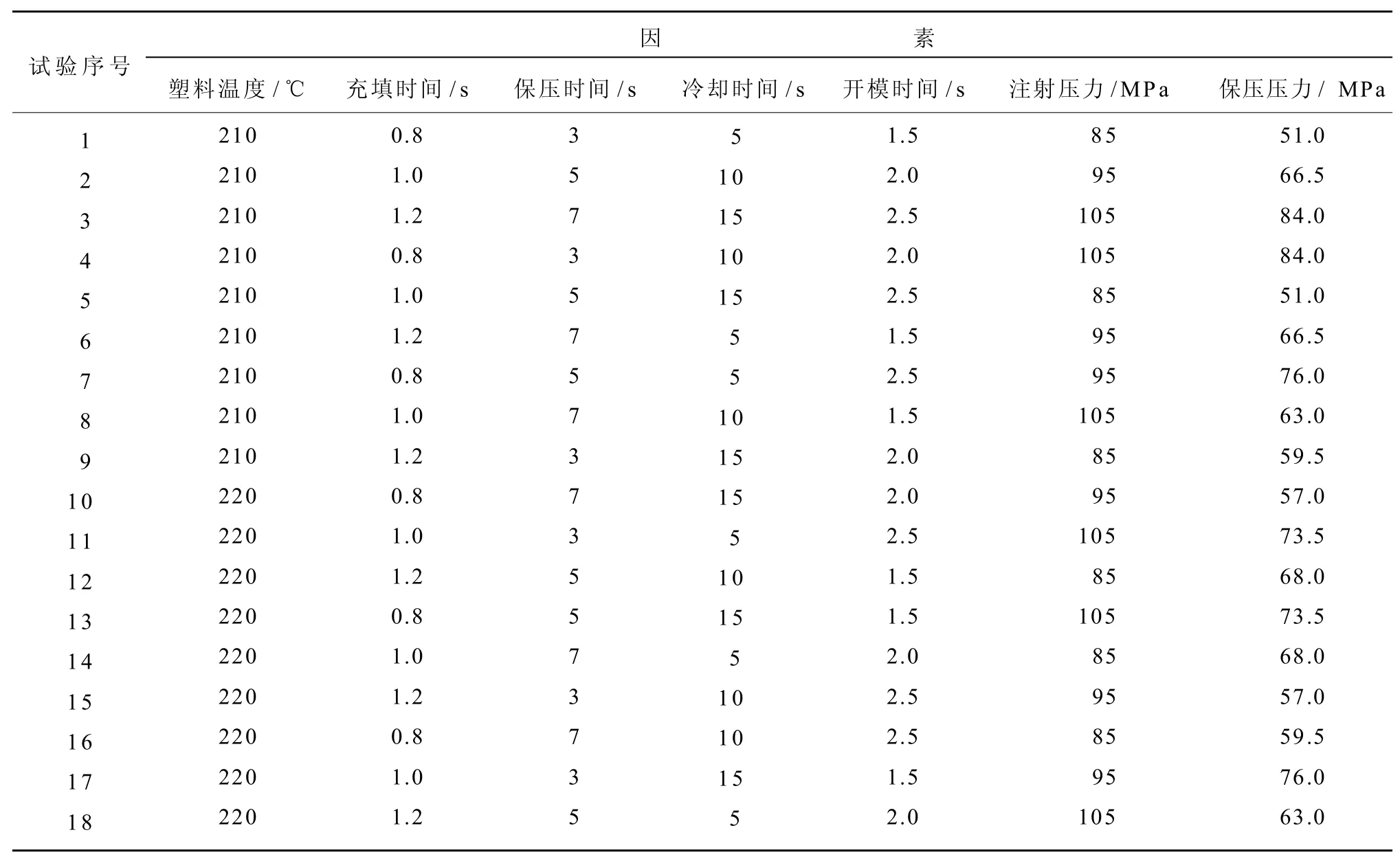
表2　原始成型参数试验数据Table 2　The original molding parameter experiment data

2.4稳健优化设计

干扰因子和控制因子可能存在着交互作用，当干扰因子的效应随某一控制因子的变动而有所不同时，可选择此控制因子的某一水平，使得干扰因子对质量特性的影响最小，以达到稳健的目的［12］。稳健的目的就是要减少质量特性的变异，当信噪比S/N 越大，所得到的变异量就越小，所以在一个试验直交表中的每一组试验都必须要有2个或2个以上的试验数据代表干扰因子影响所产生的变异。S/N 的意义就是评估干扰因子引起的变异，并把干扰因子合成主试验的单一干扰因子。干扰试验通常只取2个水平值，而且大部分的情况下会忽略交互作用，在此可以选用L12（211）直交表，并将干扰因子配置于表内进行相关试验分析。在此以表1中控制因子水平2的参数作为干扰试验设定基准，再分别将选定的7个控制因子加入干扰，干扰因子及水平如表3所示，干扰试验反应数据如表4所示。表4 中，sum为各因素对应水平试验结果总和，avg为各水平试验结果均值，effect为水平极差值（表示各因素的影响大小）。

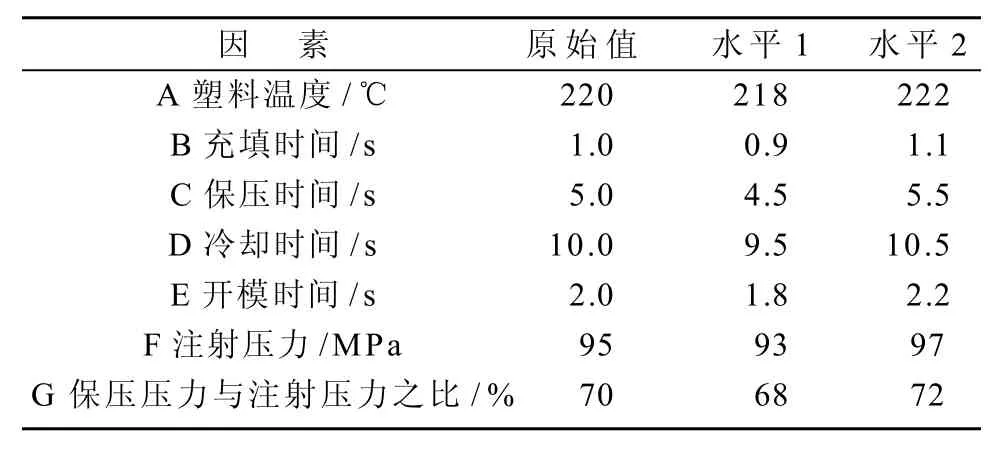
表3　干扰因子及水平Table 3　Interference factors and levels

从表4的分析结果可以得知干扰因子对于质量特性的影响程度：除了塑料温度外，其他6个因素对翘曲变形量的影响趋势相同，都是负方向，即随着控制参数数值的增加，翘曲变形量变大，故有利于减少翘曲的干扰因子组合为塑料温度（+2 ℃）、充填时间（-0.1 s）、保压时间（-0.5 s）、冷却时间（-0.5 s）、开模时间（-0.2 s）、注射压力（-2 MPa）和保压压力（-2%）。表5为加入干扰因子成型参数试验数据表。

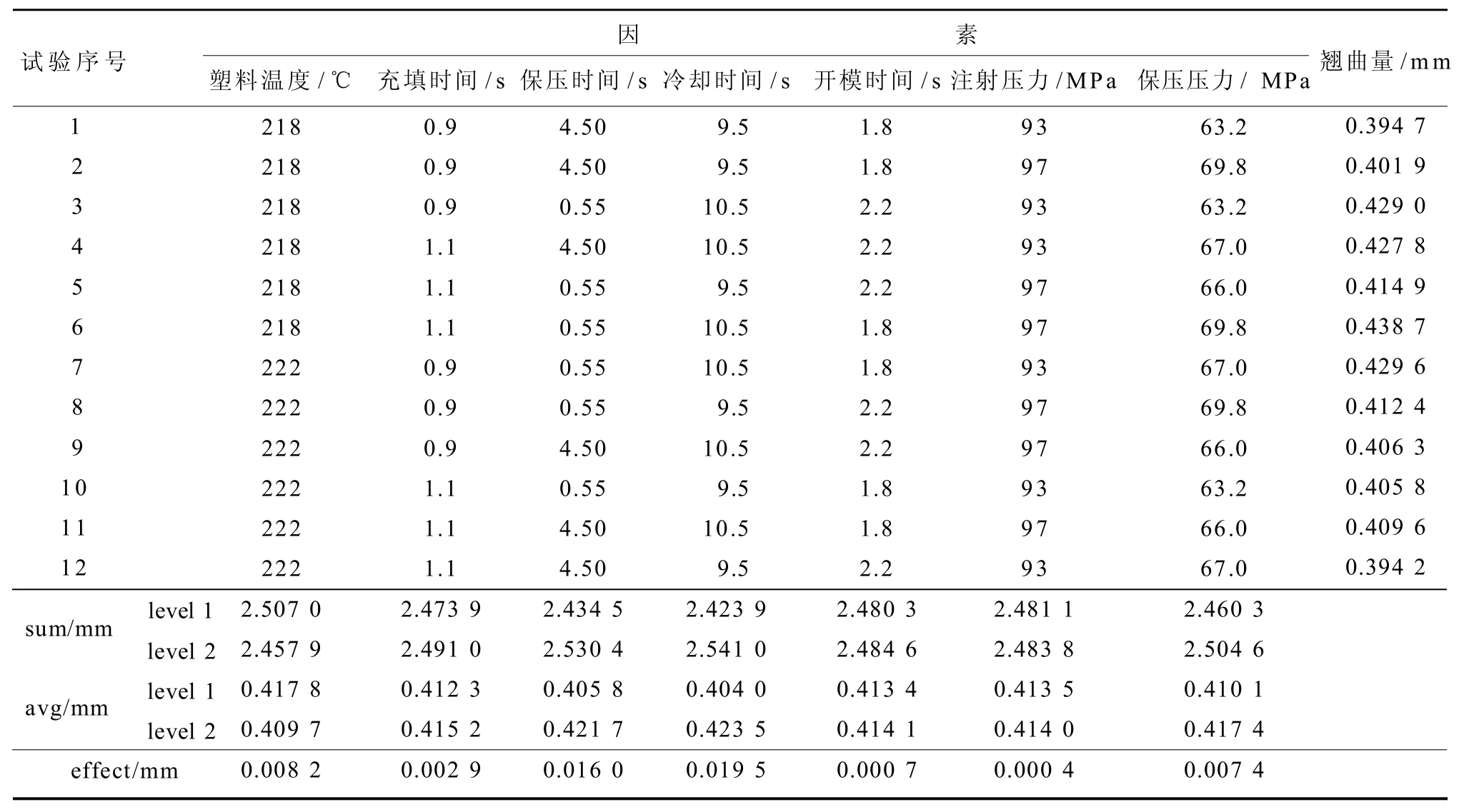
表4　干扰试验反应数据Table 4　Reaction data for interference experiment

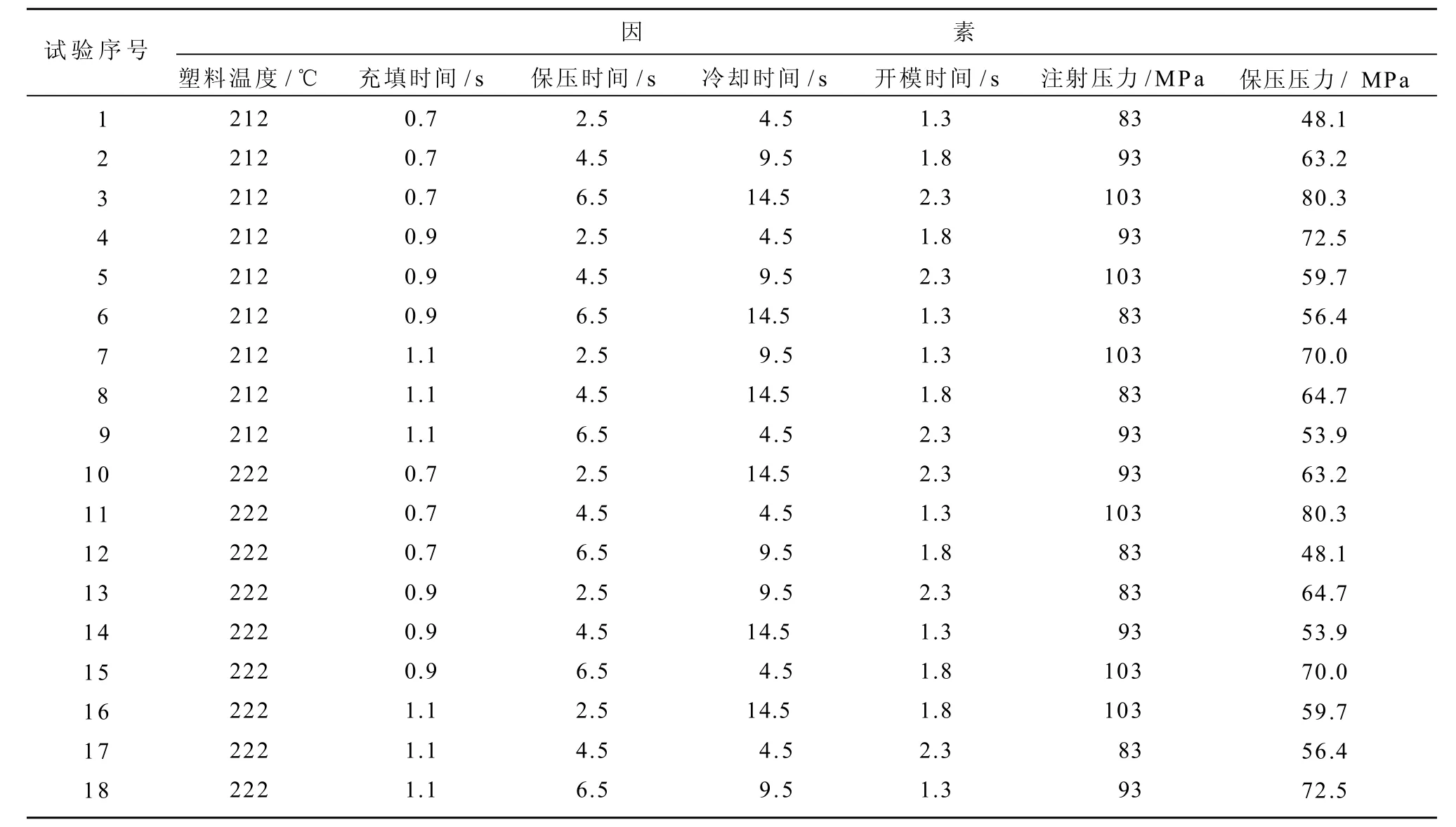
表5　加入干扰因子成型参数试验数据Table 5　Molding parameter experiment data with interference factors

2.5田口试验结果

翘曲变形量的大小及分布状况是评价卡扣塑料平板装配质量合格性的重要指标。为了获得更加准确的翘曲变形量，分别对表1中的原始成型参数和表3中加入干扰因子后的成型参数进行数值模拟试验。表6为模拟试验结果数据表，表7为控制因子对S/N的反应值。表6中：Y1为由原始成型参数获得的翘曲变形量，Y2为由加入干扰因子后成型参数获得的翘曲变形量，yavg为目标质量特性平均值，S/N为信号噪声比，即为平均值与标准偏差的比值，此值越大表示质量越好，作为田口试验衡量产品质量的统计量，T为S/N 的总和，为S/N的均值。表7中：|Δ|表示水平极差，rank表示各因素的影响大小顺序。

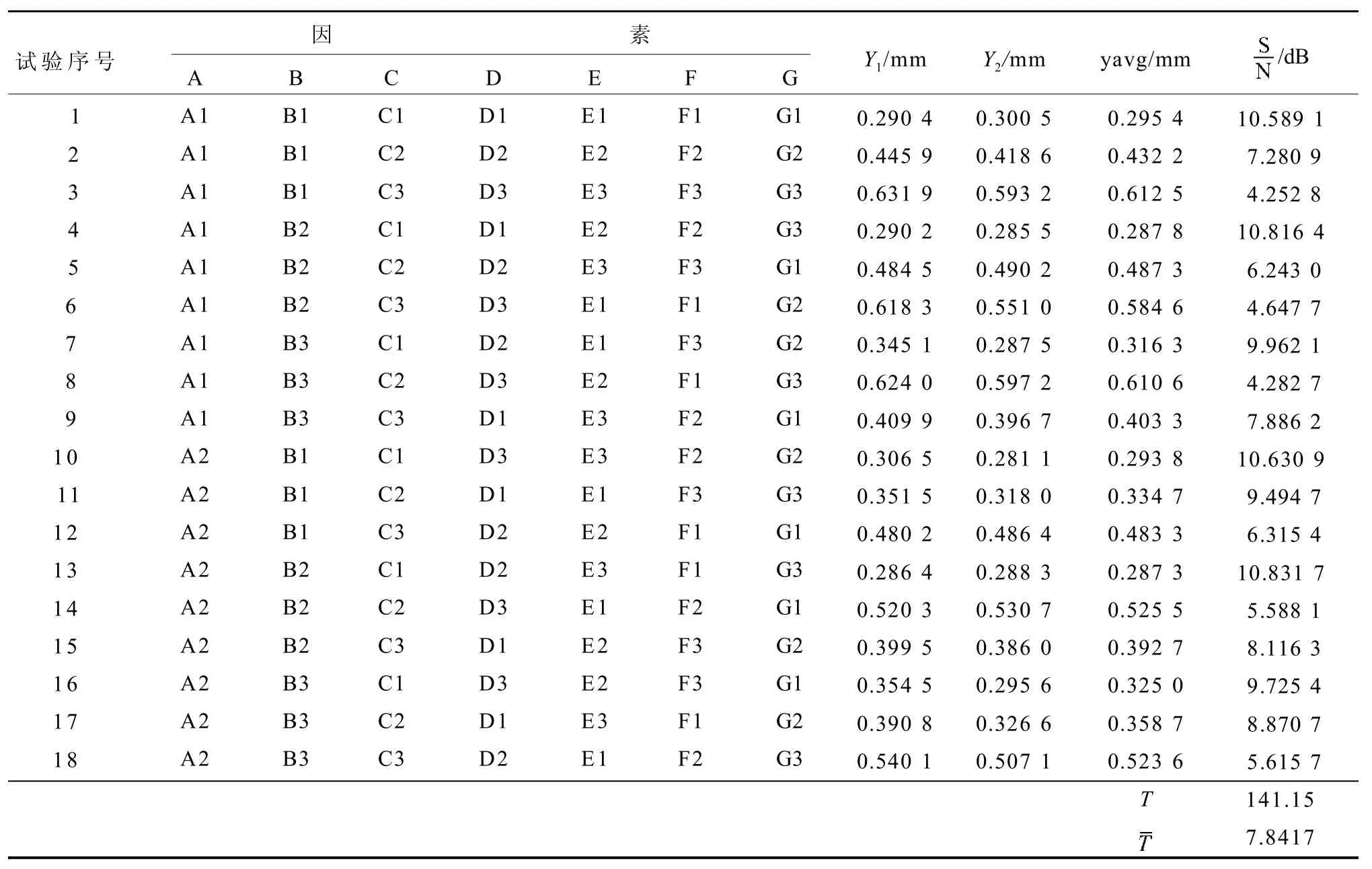
表6　 模拟试验结果数据Table 6　Data of simulation test results

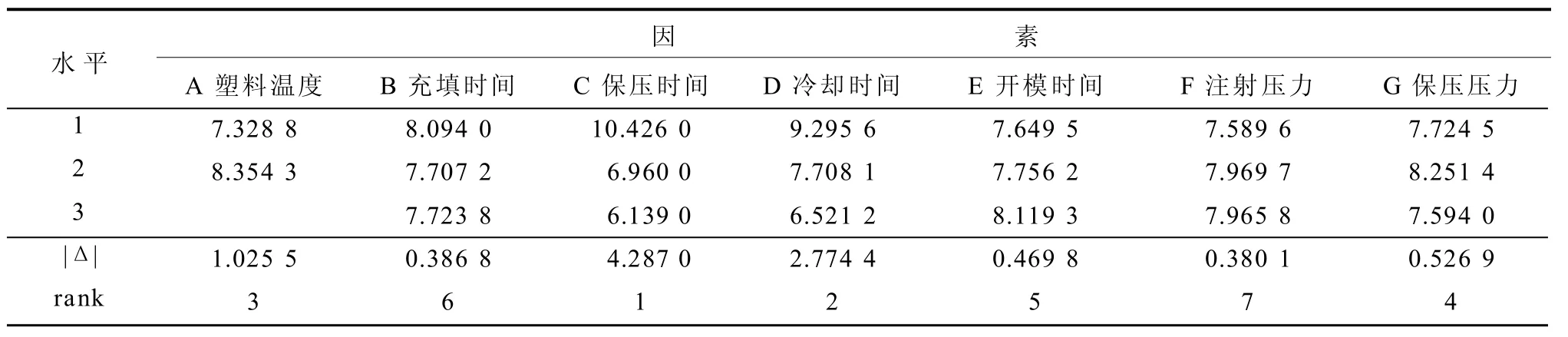
表7　控制因子对S/N的反应值Table 7　Reaction values of controlling factors to S/N

根据表7中相关数据可以得知，控制因子对质量特性所产生效应的大小顺序为：保压时间、冷却时间、塑料温度、保压压力、开模时间、充填时间、注射压力；再由控制因子所得到S/N的数值，并从各个水平当中挑选最高的S/N的水平数，可以得到优化参数组合为：A2B1C1D1E3F2G2。但是这个参数组合并不在直交表中，所以必须另行验证。通过Moldflow进一步模拟分析，所得结果如表8所示。

表8　最优组合参数模拟验证结果Table 8　The simulation verification results for the optimal combined parameters

由表8可知，原控制因子最优组合获得的制品翘曲变形量Y1=0.285 1 mm；加入干扰因子后控制因子最优组合获得的制品翘曲变形量Y2=0.298 4 mm，模拟试验获取的S/N=10.697 6。因此卡扣塑料平板最优工艺参数组合为：塑料温度220 ℃、充填时间0.8 s、保压时间3.0 s、冷却时间5.0 s、开模时间2.5 s、注射压力95 MPa、保压压力76.0 MPa。

2.6方差分析

方差分析是从观测变量的方差入手，研究诸多控制变量中哪些变量是对观测变量有显著影响的变量［12］。方差分析有2个目的，其一是以试验误差为基准来评估每个控制因子的效应，判断其是否有意义；其二是测试控制因子的显著性，一般采用F 分布的测试方式，在直交表试验中，当F值很大时，表示控制因子是有影响力的，是重要的，且远大于试验误差或是交互作用产生的影响。本试验中方差分析的结果如表9所示，进行显著性检验时，选取显著性因子为0.05，F临界值可在F检验表中查到。

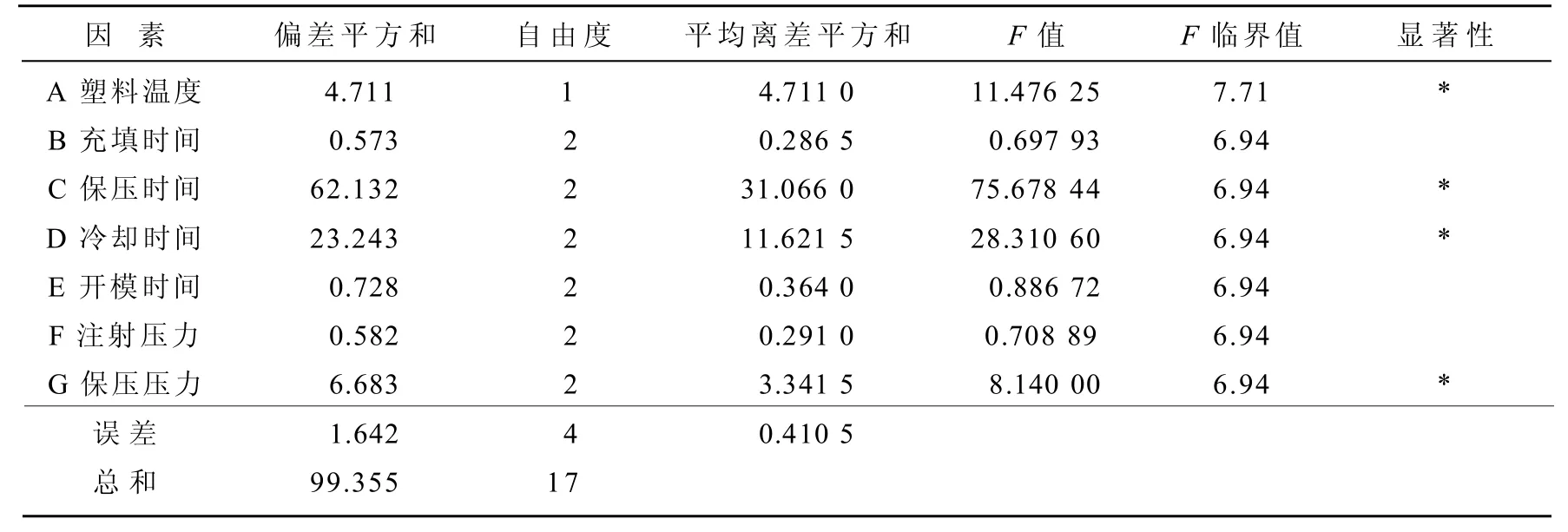
表9　方差分析Table 9　Variance analysis

比较表9中的 F值和F临界值可知，各个因素的影响差异较大，塑料温度、保压时间、冷却时间以及保压压力为显著影响因素，其他因素作用较小，是不重要的因素。因此把影响作用较小的因子并入误差项，并重新计算误差平方和。表10为误差合并后的方差分析表，表中进行显著性检验时，选取显著性因子为0.01，F临界值可以在F检验表中查到。

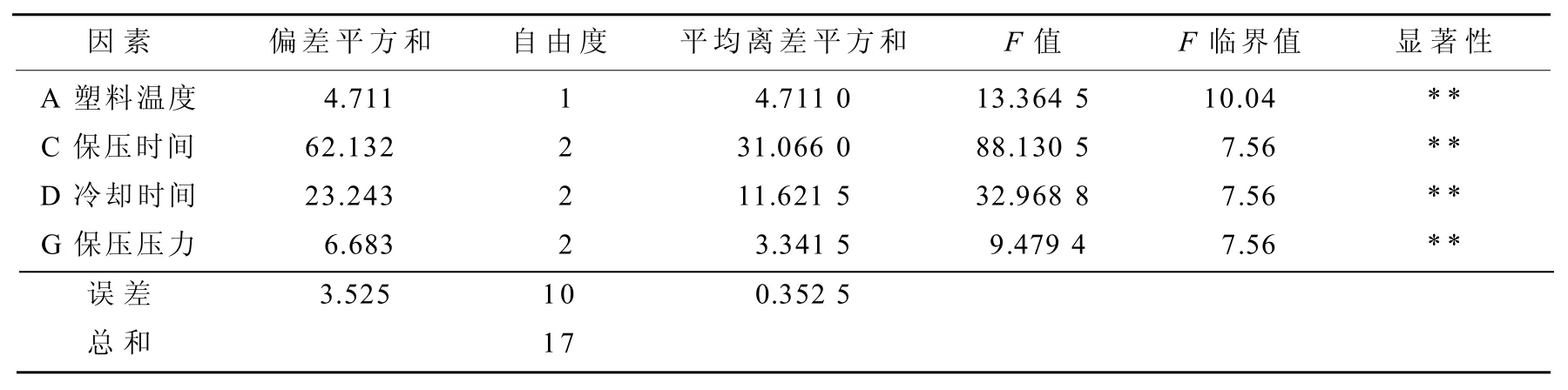
表10　误差合并方差分析Table 10　Pooled error variance analysis

由表10可知，塑料温度、保压时间、冷却时间、保压压力这4个影响因素的F值均大于临界值，且都为高度显著性，其中保压时间对制品的总变异贡献最大，冷却时间、塑料温度、保压压力的贡献依次减小。由此说明保压时间与冷却时间较长时，容易造成制品内应力增加，导致翘曲变形度上升。

2.7置信区间计算

在田口试验中，无论是用计算分析法还是效应计算分析法都能确定最优的组合，但如果直交表中没有这个最优组合，则需要按照这个组合再进行一次试验，并得出所需要的指标值［12］。本例就是如此，因此按表8再次进行试验，但为了确认试验数据的可靠性，对指标值的估计以置信区间的计算来进行验证。

置信区间可检验预测值及试验计算值的误差［12］，并判断两者是否足够接近。因为预测值是由试验的方式计算得出，如果预测值与试验值相当一致，说明置信区间有重叠，就可以确认试验的方式可行；反之，如果预测值与试验值相差较大，则说明试验的每个步骤都需要进行检讨，包括质量特性、控制因子选择等。

根据文献［12］可知，在95%置信水平下置信区间可按如下步骤计算。

1）因子取值的置信区间

偏差

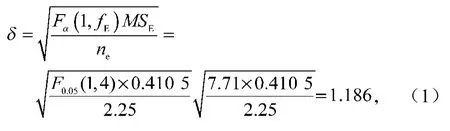
式中：fE表示误差自由度；

MSE表示误差方差，且MSE= SE/fE，其中SE表示误差平方和；

ne是有效试验次数，有效试验次数=试验总次数/（1+显著因素自由度和）；

为检验水平，此处取值为0.05。

2）验证试验值置信区间

偏差

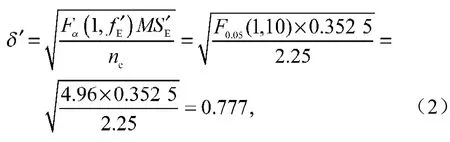
根据表8最佳组合参数模拟验证可知，验证试验值S/N为10.697 6 dB，因此验证试验值的置信区间为9.920 6 ～11.474 6 dB。

3）最佳预测值置信区间

在优化参数组合的控制下，采用一半准则，从表7控制因子对S/N反应表中挑选一半反应较大的控制因子按式（3）进行最佳预测值计算。

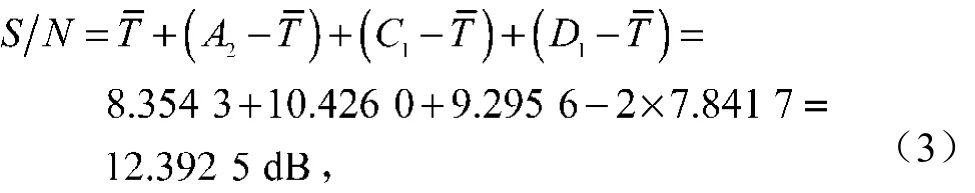
式中：A2为控制因子A在水平2下对S/N的反应值；

C1为控制因子C在水平1下对S/N的反应值；

D1为控制因子D在水平1下对S/N的反应值。

偏差

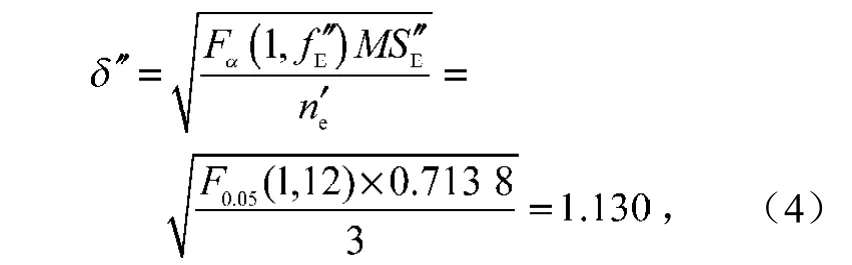
因此，最佳预测值置信区间为11.262 5～13.522 5 dB。

综上所述，在95%置信水平下，验证试验值与最佳预测值的S/N置信区间高度重合，这表明试验验证值和预测值两者一致性高。

3　最优组合参数成型模拟分析

将最优组合工艺参数作为Moldflow成型条件，进行注塑成型模拟分析。图2为卡扣塑料平板总体翘曲变形云图。经模流分析可知，制品总变形最大量为0.285 1 mm，而收缩不均引起的变形量就达到了0.252 7 mm。制品发生翘曲变形的主要原因是注塑成型过程中发生了收缩不均现象。

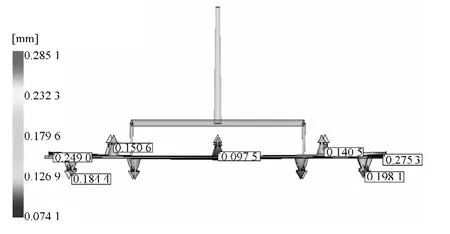
图2　卡扣塑料平板总体翘曲变形云图（放大20倍）Fig. 2　Nephogram of total warping deformation of snap-in plastic plates（20×）

从图2中可以看出，制品发生翘曲严重的地方分布在平板两侧，尤其是制品的左上角与右下角边缘处，变形量达到0.25 mm左右；而卡扣的变形量随着分布位置不同也不同，面板上方中间位置卡扣几乎没有变形，面板上方两侧的卡扣变形量为0.15 mm左右，翘曲方向主要是向着制品的中心，另一边面板下方左右对称各布置4个卡扣，靠边缘的卡扣最大变形量接近0.20 mm，靠中心的卡扣变形量不到0.10 mm，与面板上方卡扣不同之处在于它们是背离制品中心发生翘曲，但总体上制品的翘曲幅度不大，符合几何形状误差要求。

另外模流分析结果显示，制品的顶出体积收缩率分布较均匀，较大的收缩率位于制品的边缘与制品的中心，分别约为2.9%和2.5%，面板总体收缩率不超过3%，符合制品几何尺寸误差要求。

4　结论

影响注射成型制品翘曲变形的因素很多，大多数注射产品在脱模静置一段时间后，都会由于成型内部应力释放导致原本平稳的平面向里面或是外面弯曲。产品的外观、浇注系统、冷却系统的合理设计以及成型工艺参数的正确选择是改善制品翘曲的重要手段。

本文以卡扣塑料平板为例，运用Moldflow 结合田口试验方法进行了取样分析，可得如下结论：

1）田口直交表可以有效地降低试验次数，搭配方差分析可以找出影响质量的显著因子，并能区分各因子对质量影响程度的高低。保压时间是影响制品翘曲变形最具有影响力的因子，其次为冷却时间、塑料温度以及保压压力。

2）由计算机辅助工程（CAE）优化参数模拟结果可知，各因素的最佳参数为：塑料温度220 ℃、充填时间1.0 s、保压时间3.0 s、冷却时间5.0 s、开模时间2.5 s、注射压力85 MPa 和保压压力取80%注射压力。

3）最优组合数值模拟结果显示，保压时间和冷却时间都选择较小参数值，这表明保压时间和冷却时间较长易造成制品内应力增加，有导致翘曲变形的可能性。

4）通过置信区间计算，肯定了验证试验值和预测值两者的一致性，说明该方法对提高注射产品质量和降低研发成本具有可行性。

［1］赵苗，辛勇. 注塑制品翘曲变形的研究进展［J］. 中国塑料，2012，26（4）：66-71. ZHAO Miao，XIN Yong. Research Progress in Warpage of Injection Molded Parts［J］. China Plastics，2012，26（4）：66-71.

［2］张继祥，秦海涛，钟厉，等. 薄壁件注塑翘曲变形综合优化分析［J］. 塑料工业，2014，42（5）：56-61. ZHANG Jixiang，QIN Haitao，ZHONG Li，et al. Comprehensive Optimization Analysis of Injection Moulding Warp Deforming of the Thin-Wall Plastic Parts［J］. China Plastics Industry，2014，42（5）：56-61.

［3］王桂龙，赵国群，李辉平，等. 薄壁注塑制品翘曲影响因素分析与工艺优化［J］. 中国机械工程，2009，20（4）：488-492. WANG Guilong，ZHAO Guoqun，LI Huiping，et al. Influence Factor Analysis of Warpage and Optimization of Process Parameters in Plastic Injection Molding of Thin-Wall Plastic Parts Based on Taguchi Optimization Method［J］. China Mechanical Engineering，2009，20（4）：488-492.

［4］沈洪雷，刘峰. 基于CAE热流道注塑件翘曲变形的研究［J］. 工程塑料应用，2014，42（4）：62-65. SHEN Honglei，LIU Feng. Study on the Warpage of Injection Molded Parts Injected by Hot Runner Based on CAE［J］. Engineering Plastics Application，2014，42（4）：62-65.

［5］林权，林铮，陈冲. 应用 Moldfolw 及 ABAQUS 进行注塑模结构优化设计［J］. 塑料，2011，40（6）：106-110. LIN Quan，LIN Zheng，CHEN Chong. Optimization of the Injection Mold Design Based on Moldflow and ABAQUS［J］. Plastics，2011，40（6）：106-110.

［6］王立恒，游珊珊. 2014年ABS树脂生产与市场分析［J］. 化学工业，2015，33（7）：31-35. WANG Liheng，YOU Shanshan. The Analysis of ABS Resin Production and Market［J］. Chemical Industry，2015，33（7）：31-35.

［7］曾亚森，何和智. 基于翘曲的注塑成型工艺参数优化组合［J］. 高分子材料科学与工程，2009，25（6）：163-166. ZENG Yasen，HE Hezhi. Optimal Combination of Injection Molded Process Parameter Based on Warp［J］. Polymer Materials Science and Engineering，2009，25（6）：163-166.

［8］刘瑞江，张业旺，闻崇炜，等. 正交试验设计和分析方法研究［J］. 实验技术与管理，2010，27（9）：52-55. LIU Ruijiang，ZHANG Yewang，WEN Chongwei，et al. Study on the Design and Analysis Methods of Orthogonal Experiment［J］. Experimental Technology and Management，2010，27（9）：52-55.

［9］肖良红，胡建强. 基于翘曲变形的薄壁塑件成型工艺优化［J］. 中国塑料，2014，28（3）：106-111. XIAO Lianghong，HU Jianqiang. Forming Process Optimizing for Injection Molding of the Thin-Walled Plastic Parts Based on Warping Deformation［J］. China Plastics，2014，28（3）：106-111.

［10］陈昌乾，刘斌，王桂林. 电视机小后壳注射成型工艺的优化设计［J］. 工程塑料应用，2015，43（2）：51-54. CHEN Changqian，LIU Bin，WANG Guilin. Optimization Design of TV Deputy Shell Injection Molding Process Parameters［J］. Engineering Plastics Application，2015，43（2）：51-54.

［11］钱秋波. 基于模拟的注塑模浇注系统及成型工艺参数优化研究［D］. 苏州：苏州大学，2011. QIAN Qiubo. Optimization Study on Gating System and Molding Process Parameters of Injection Mold Based on Simulation［D］. Suzhou：Soochow University，2011.

［12］李云雁，胡传荣. 试验设计与数据处理［M］. 2版. 北京：化学工业出版社，2008：83-98. LI Yunyan，HU Chuanrong. Experiment Design and Data Processing［M］. 2nd ed. Beijing：Chemical Industry Press，2008：83-98.

（责任编辑：邓光辉）

DOE and MPI-Based Robust Optimal Design for Injection Molding Process

LIN Quan
（School of Mechanical and Electrical Engineering，Wuyi University，Wuyishan Fujian 354300，China）

The warping deformation is an important index to evaluate the quality conformance of snap-in plastic plate assembly. Applies the Taguchi's Design of Orthogonal Experiment （DOE） with the combination of mold flow project analysis module to study the warping deformation of the products. Through robust optimal design of injection molding process parameters and the experimental analysis， obtains the optimal process parameter combination， and by utilizing the calculations in the confidence intervals， verifies the reliability of the optimal parameter combination. The research results show that the dwell time is the most significant influencing factor， followed by cooling time， the plastic temperature and dwell pressure. The long dwell time and cooling time is easy to cause the increase of internal stress in products， which may leads to the possibility of warping deformation.

warping deformation；Taguchi's orthogonal experiment；Moldflow；robust optimization

TQ320.66

A

1673-9833（2016）01-0070-08

10.3969/j.issn.1673-9833.2016.01.013

2015-12-01

福建省教育厅A类科技基金资助项目（JA13323），南平市科技计划基金资助项目（N2013X01-7）

林权（1980-），男，福建福州人，武夷学院讲师，硕士，主要研究方向为塑料成型工艺与模具设计，E-mail：12959392@qq.com