非线性时间序列B样条优化网络预测模型及工业应用

孔玲爽，龚小龙，周维龙

（湖南工业大学 电气与信息工程学院，湖南 株洲 412007）

非线性时间序列B样条优化网络预测模型及工业应用

孔玲爽，龚小龙，周维龙

（湖南工业大学 电气与信息工程学院，湖南 株洲 412007）

为有效实现非线性时间序列的实时预测，建立了一种B样条优化网络预测模型。在网络结构的设计中，将各个样条基函数的权值参数和节点位置同时视为待优化的独立变量，并选择预测误差平方和为评价函数，设计了一种全局优化算法，对网络结构进行优化。工业仿真实验结果表明，所提出的优化网络预测模型具有较高的预测精度，而且结构简单，待优参数少，是一种有效的非线性时间序列预测方法。

非线性时间序列；B样条网络；预测模型；工业过程

1　背景知识

时间序列预测问题广泛存在于经济、金融、气象、气候、环境以及工业生产等领域。时间序列是将某种统计指标的数值按时间先后顺序排列所形成的数列。时间序列预测方法通过编制和分析时间序列，根据其所反映出来的发展过程、方向和趋势，进行类推或延伸，借以预测下一段或以后若干时间可能达到的水平［1］。由于时间序列本身的随机特性，许多预测方法都是基于统计学原理的，比如自回归（autoregressive，AR）模型、滑动平均（moving average，MA）模型和差分自回归滑动平均（autoregressive integrated moving average，ARIMA）模型等。这些预测方法主要适用于同方差和单变量的线性问题。尽管在许多实际应用中，线性模型基本上可行，然而近些年来，研究者越来越清楚地看到它们诸多的局限性（例如它们无法产生带有非堆成周期的数据，它们通常是时间可逆的）。现实问题要求人们不得不以“非线性”来看待时间序列，并不断地改进模型。

针对时间序列的非线性建模方法主要有门限自回归（self-exciting threshold autoregressive，SETAR）模型、双线性（bilinear，BL）模型和指数自回归（exponential artoregressive，EAR）模型等［2］。其中，SETAR是最简单的一种非线性时间序列模型。

随着智能技术的发展和优势，人工神经网络逐渐成为非线性时间序列预测的有效工具［3-8］。理论上，如果隐层神经元数目足够多，人工神经网络可以以任意精度逼近非线性系统。然而，通常的神经网络具有多层感知，结构复杂且难于理解。为此，研究者提出一种基于网格的径向基函数网络来近似非线性系统，但对于如何选择网格点没有进一步的讨论和研究。另一类人工神经网络是模糊联想记忆神经网络，它采用基函数的线性组合来近似非线性系统，这类网络的结构更容易理解。对于这类网络，基函数有多种选择，最常用的基函数是径向基核函数，但径向基核函数难以确定中心值和宽度参数［9-11］。另一类常用的基函数是B样条基函数，它是用分段多项式来表示的函数，网络结构为B样条基函数的线性组合［12-13］。在B样条网络的结构设计中，节点的选择对于网络的预测精度非常重要。但在大多数研究中，由于理论的缺乏，节点往往被预先设定，或者当近似精度不能满足要求时，均匀地增加节点，这2种方法都不能实现节点的最优设置，所以网络的近似精度往往不如人意［14-15］。

本文拟采用一种节点优化B样条神经网络实现某冶金过程非线性时间序列参数的预测。该网络将B样条基函数的节点视为独立决策变量，在网络训练过程中，与网络参数一起优化；为避免优化过程陷入局部最小，设计了一种随机优化算法进行全局寻优计算。仿真结果表明，在具有相同精度的条件下，与径向基核函数网络相比，B样条优化网络具有更简单的结构和更低的计算成本。

2　B样条函数

B样条函数是一个分段多项式，它可表示为B样条基函数的线性组合。为了简单，本研究先讨论一维样条函数。

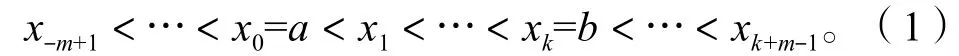
式中k和m均为正整数。

这样，在［a， b］上，m阶的标准样条基函数可表示为i，m，i=-m+1， -m+2， …， k。其定义为

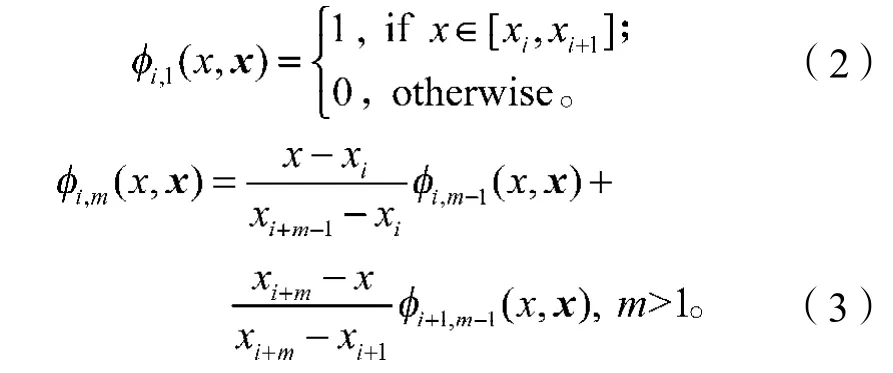
对于任意m≥1，B样条基函数满足：

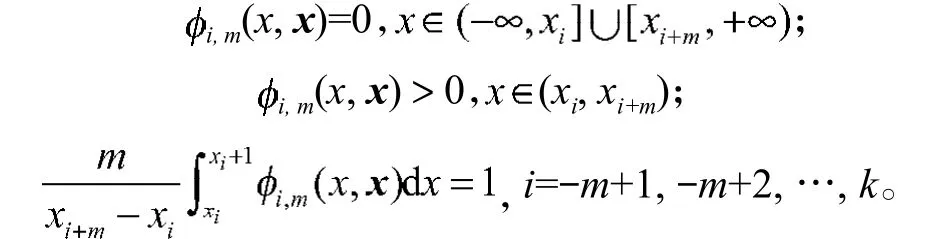
实质上，基函数是对单位1的一种分割，即有

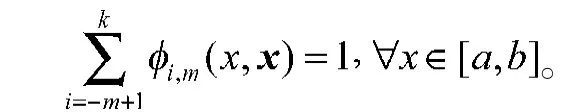
当m≥3时，基函数在（-∞， +∞）上是光滑的。

这样，一个m阶的一维B样条函数 （x， x）定义为基函数的线性组合，即：

式中ci是待定常数，其中i=-m+1，-m+2，…， k。

3　非线性时间序列B样条优化网络

设有一非线性时间序列｛y1， y2， …， yn｝，有

式中：n+1为预测误差；

f（·）为预测函数。

时间序列预测问题就是如何构建预测模型f（·）使其能够利用过去的时间序列数据预测现在或将来的结果。在这里，采用多维B样条函数网络逼近f（·）。一个n维B样条网络函数f（·）可以用式（2）和式（3）的一维样条基函数的张量积表示，即

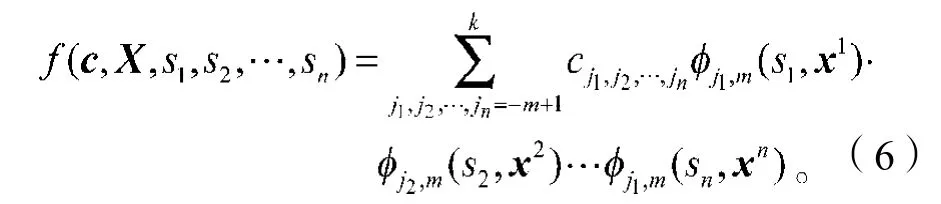
X=（x1， x2， …， xn）为节点矩阵；

sj（j=1， 2， …， n）为第j维变量值域内的值。

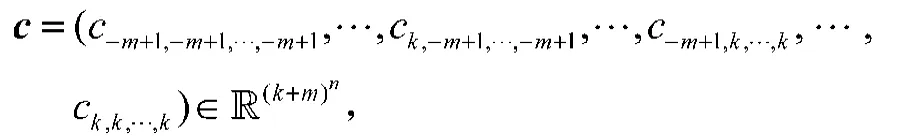
在现有大多数的研究中，式（6）的网络结构都是被预先设定，也就是说，各维变量的节点xj是预先设定好的。在训练网络过程中，仅将视为变量，这种被预先固定结构的B样条网络性能往往是不理想的。为了优化网络结构，将网络（6）中的xj和同时视为决策变量，并进行全局寻优，获得一种带有优化节点的样条网络结构。算法步骤如下。

1）选定一组序列 ｛ y1， y2， …， yn， yn+1， … ， yN｝，令，在超立方体［a， b］n上， 随机初始化节点矩阵X ；给定一个常数 c，随机初始化

2）选定最大优化次数M，令M0=0，初始化1个小正数=random（-1， 1）。

3）根据式（5）计算预测误差的平方和，即

4　工业仿真实验

为检验模型的有效性，采用某冶金配料过程的数据进行仿真验证。在该配料过程中，由于生产条件和检测技术的限制，原料质量参数无法在线检测，只能进行离线分析，检测结果非常滞后，无法及时指导生产。但这些滞后的检测数据是按时间顺序排列的，构成了时间序列，因此，如何利用这些时间序列进行原料质量参数的实时预测非常有意义。在该工业仿真实验中，对一种原料中氧化钙和氧化硅的百分含量进行预测，分别取200组数据点训练网络。其中，样条基函数为三阶，即m=3；网络为二维，即n=2；在训练过程中，设定M=10 000。网络训练完成后，另取50组数据验证模型的泛化能力，如图1和图2所示。从2个图中可以看出，预测结果非常接近实际值，说明了模型的有效性。

图1　氧化钙含量预测结果Fig. 1　Prediction results of calcium oxide content

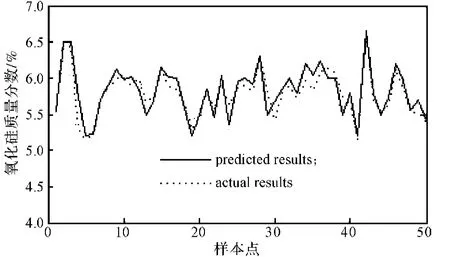
图2　氧化硅含量预测结果Fig. 2　Prediction results of sodium oxide content

为进一步评价方法的性能，将所提出的网络和径向基函数网络进行比较，结果如表1所示。表1中采用预测值与实际值的最大相对误差和均方根误差作为评价指标，可看出所提出网络的2种误差明显小于径向基网络的误差，说明其具有较好的预测效果。

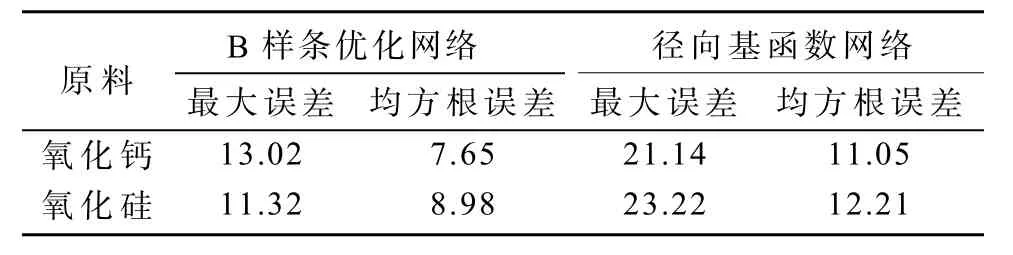
表1　2种网络预测性能比较Table 1　Prediction performance comparison of 2 kinds of network %

5　结语

本文将一种B样条优化网络用于非线性时间序列预测，该网络在参数优化中，结构也同时被优化，克服了结构固定网络的不足。工业应用仿真实验结果表明，所提出的优化网络具有较好的泛化能力，且结构简单，优化参数少，是一种有效的非线性时间序列预测方法。

［1］张美英，何杰. 时间序列预测模型研究综述［J］. 数学的实践与认识，2011，41（18）：189-195. ZHANG Meiying，HE Jie. Summary on Time Series Forecasting Model［J］. Mathematics in Practice and Theory，2011，41（18）：189-195.

［2］张浒. 时间序列短期模型研究与应用［D］. 武汉：华中科技大学，2013. ZHANG Hu. The Research and Application of Short-Term Forecasting Model for Time Series［D］. Wuhan：Huazhong University of Science and Technology，2013.

［3］牛家洋. 基于神经网络的非线性系统时间序列的预测方法研究［D］. 济南：山东师范大学，2013. NIU Jiayang. Forecast Method Research of Nonlinear System Time Series Based on Neural Network［D］. Jinan：Shandong Normal University，2013.

［4］李哲敏，许世卫，崔利国，等. 基于动态混沌神经网络的预测研究：以马铃薯时间序列价格为例［J］. 系统工程理论与实践，2015，35（8） ：2083-2091. LI Zhemin，XU Shiwei，CUI Liguo，et al. Prediction Study Based on Dynamic Chaotic Neural Network：Taking Potato Time-series Prices as an Example［J］. System Engineering-Theory & Practice，2015，35（8）：2083-2091.

［5］张大斌，李红燕，刘肖，等. 非线性时间序列的小波-模糊神经网络集成预测模型［J］. 中国管理科学，2013，21（S2）：647-651. ZHANG Dabin，LI Hongyan，LIU Xiao，et al. A Integrated Prediction Method of Wavelet-Fuzzy Neural Network for Nonlinear Time Series［J］. Chinese Journal of Management Science，2013，21（S2）：647-651.

［6］杨娟丽，徐梅，王福林，等. 基于BP神经网络的时间序列预测问题研究［J］. 数学的实践与认识，2013，43（4）：158-164. YANG Juanli，XU Mei，WANG Fulin，et al. Research Based on BP Neural Netword Time Series Forecastin［J］. Mathematics in Practics and Theory，2013，43（4）：158-164.

［7］洪嘉灏，李雄英，王斌会. 基于人工神经网络和随机游走模型的汇率预测［J］. 经济数学，2016，33（1）：30-35. HONG Jiahao，LI Xiongying，WANG Binhui. Exchange Rate Forecast Based on Artificial Neural Network and Random Walk Model［J］. Journal of Quantitative Economics，2016，33（1）：30-35.

［8］宋怡霖，陈新楚，郑松. 对角递归神经网络在控制系统中的应用现状分析［J］. 电气传动和自动控制，2016，38（2）：41-43，68. SONG Yilin，CHEN Xinchu，ZHENG Song. An Analysis on the Status of Application of Diagonal Recurrent Neural Network in Control Systems［J］. Electric Drive & Automatic Control，2016，38（2）：41-43，68.

［9］佩世鑫，李仲怡，催芬萍，等. 基于RBF人工神经网络的X级以上太阳耀斑预报研究［J］. 西北师范大学学报（自然科学版），2014，50（6）：26-32. PEI Shixin，LI Zhongyi，CUI Fenping，et al. A Study of the Prediction for X-Class and Above Flares Based on RBF Artificial Neural Network［J］. Journal of Northwest Normal University（Natural Science），2014，50（6）：26-32.

［10］李光，杨韵. 基于RBF神经网络的柔性机械臂位置控制［J］. 湖南工业大学学报，2014，28（3）：41-46. LI Guang，YANG Yun. Flexible Manipulation Position Control Based on RBF Neural Network［J］. Journal of Hunan University of Technology，2014，28（3）：41-46.

［11］陈帝伊，柳烨，马孝义. 基于径向基函数神经网络的混沌时间序列相空间重构双参数联合估计［J］. 物理学报，2012，61（10）：22-31. CHEN Diyi，LIU Ye，MA Xiaoyi. Parameter Joint Estimation of Phase Space Reconstruction in Chaotic Time Series Based on Radial Basis Function Neural Networks［J］. Acta Physica Sinica，2012，61（10）：22-31.

［12］张浩，张代远. 基于三次样条权函数神经网络的股价预测［J］. 计算机技术与发展，2014，24（6）：28-31. ZHANG Hao，ZHANG Daiyuan. Stock Prediction Based on Neural Networks with Cubic Spline Werght Functions［J］. Computer Technology and Development，2014，24（6）：28-31.

［13］王世东，王焕宝. 基于SOM网络的三次B样条曲线重建［J］. 计算机工程与应用，2012，48（15）：192-244. WANG Shidong，WANG Huanbao. Cubic B-Spline Curve Reconstruction Based on SOM［J］. Computer Engineering and Applications，2012，48（15）：192-244.

［14］YIU K F，WANG S，TEO K L，et al. Nonlinear System Modeling Via Knot-Optimizaing B-Spline Networks［J］. IEEE Transaction on Neural Networks，2001，12（5）：1013-1022.

［15］WANG S，SHAO Q，ZHOU X. Knot-Optimizing Spline Networks（KOSNETS） for Nonparametric Regression［J］. Journal of Industrial & Management Optimization，2008，4（1）：33-52.

（责任编辑：申剑）

An Optimized Model Based on Nonlinear Time Series for B-Spline Networks Prediction and Its Industrial Application

KONG Lingshuang，GONG Xiaolong，ZHOU Weilong
（School of Electrical and Information Engineering，Hunan University of Technology，Zhuzhou Hunan 412007，China）

An optimizing model for B-spline networks prediction has been proposed for the effective realization of the real-time prediction based on nonlinear time series. A global optimization algorithm has been adopted for the optimization of the design of the network structure， with the weight parameters and node location of spline functions synchronous independent variables to be optimized. The industrial simulation results show that the proposed optimized model for networks prediction has a relatively higher prediction accuracy. With its structure much simpler and less parameters to be optimized， this is an effective prediction method based on nonlinear time series.

nonlinear time series；B-spline networks；prediction model；industrial process

TP274

A

1673-9833（2016）03-0082-04

10.3969/j.issn.1673-9833.2016.03.015

2016-03-27

国家自然科学基金资助项目（61203136），湖南省自然科学基金资助项目（2015JJ5025）

孔玲爽（1979-），女，河北邢台人，湖南工业大学副教授，博士，主要从事复杂工业过程建模与优化控制方面的研究，E-mail：konglingsh@126.com

周维龙（1978-），男，湖南邵阳人，湖南工业大学讲师，硕士，主要研究方向为无线传感器网络与嵌入系统设计，E-mail：604085429@qq.com