双相机工业摄影测量系统测量性能测试方法研究

黄桂平，轩亚兵，马彤彤

（1.华北水利水电大学，河南 郑州 450045；2.辰维科技股份有限公司，河南 郑州 450001）

双相机工业摄影测量系统测量性能测试方法研究

黄桂平1，2，轩亚兵1，马彤彤1

（1.华北水利水电大学，河南 郑州 450045；2.辰维科技股份有限公司，河南 郑州 450001）

双相机工业摄影测量系统的广泛应用使其测量性能越来越受到关注，如何准确合理地评价系统的测量性能，并制定相应检定规范是目前亟待解决的问题。针对双相机系统测量性能的测试问题提出一套系统的方法：首先对双相机系统的摄影距离和基线长度等结构参数进行实验，并选择最佳参数进行系统的测量性能测试；然后对双相机的测量重复性、三维坐标测量准确度与长度测量准确度进行测评；最后通过以上3个评价指标对双相机系统测量性能进行总体分析与评价。该方法测得某型双相机的自身测量重复性为0.027mm，三维坐标测量准确度为0.060mm，长度测量准确度为0.062mm。据此推荐用测量重复性、三维坐标测量准确度、长度测量准确度3个指标对系统进行评价。

双相机；工业摄影测量；测量重复性；坐标测量；长度测量

0　引　言

双相机工业摄影测量系统是数字近景工业摄影测量系统的一种联机测量模式［1］。国内双相机工业测量系统最早于1999年开始应用于三维尺寸检测［2］，之后，在双相机的应用逐步拓展，众多学者开始关注理论研究。黄桂平［3］对双相机工业摄影测量系统的测量原理进行了分析；于英［4］对双相机工业摄影测量系统的相机标定、图像获取、特征提取与匹配等关键技术进行了研究。但是，由于我国双相机工业摄影测量系统起步较晚，现阶段相机结构的构建多根据经验而定。在测量性能测试方面，多采用仿真的方法进行研究［5-6］，在具体应用方面有很大的局限性。因此，如何对双相机工业摄影测量系统进行系统合理的测量性能的测试与评价，成为研发者和用户共同关心的重要问题。

本文以郑州辰维科技公司自主研发的MPS/M04双相机工业摄影测量系统为例，在研究双相机系统测量性能影响因素的基础上，提出一套测试与评定的方法。该方法用测量重复性、三维坐标测量准确度、长度测量准确度3个指标对双相机系统的准确度进行测试与评价。

1　评定的原理与指标选择

系统的测量性能从精密度和测量准确度两个方面进行评价。精密度是指在一定条件下，对同一或类似被测对象重复测量所得示值或测得值间的一致程度［7］；测量准确度是指测量值与其真值间的一致程度。衡量测量精密度和准确度的指标有很多，结合双相机系统自身特点和实验条件本文选择了3个指标对双相机系统的测量性能进行评价，分别是测量重复性、坐标测量准确度、长度测量准确度。

1.1测量重复性

测量重复性是双相机系统内部检核评定指标，反映的是系统结构的稳定性。对测试墙面进行连续多组测量，然后以其中一组（一般选用第1组）为标准，进行公共点转换，将其他各组与第1组转换到同一坐标系下，然后进行公共点坐标值的比对。设各组测量值的坐标为（Xij，Yij，Zij），其中i=1，2，…，m；j= 1，2，…，n；m为测量组数，n为同名点的个数。则有：

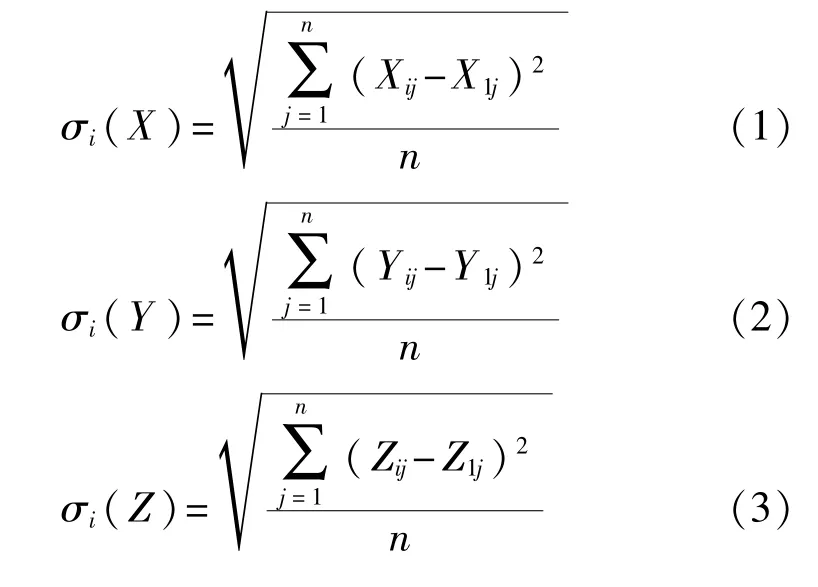
式中σi（X）、σi（Y）、σi（Z）为第i组测量值相对第1组在X、Y、Z方向上的点位偏差。

则点位标准偏差：

最后求取所有组点位标准偏差的平均值就是双相机系统的测量重复性的表征量。该值越小双相机系统的稳定性和测量重复性越好。

1.2三维坐标测量准确度

三维坐标测量准确度是指双相机测量系统测量的点位坐标与其真值的一致程度，属于外部检核评价指标。由于坐标真值未知，所以被测试系统的测量准确度由坐标测量性能较优且测量误差已知的系统测量值作为比对标准，通过误差原理推理得到。

设单相机测量系统的坐标测量结果（Xi，Yi，Zi），双相机的坐标测量结果（Xi＇，Yi＇，Zi＇），进行公共点转换，将两组测量结果转换到同一坐标系下，然后计算双相机系统的三维坐标测量准确度。

具体的推导公式为

式中i=1，2，…，n；n为公共点的个数；Δdi表示双相机相对于单相机的第i个公共点的点位偏差。

式中σ表示双相机相对于单相机的点位偏差的均方根值，近似等于双相机相对于单相机的中误差。

由式（5）和误差合成公式可知：

式中：md——单相机的三维坐标测量误差；

ms——双相机的三维坐标测量误差。

在本文测试中，所选择的单相机的误差已知，且小于双相机测量误差，所以按照式（9）由测得的点位偏差的均方根值σ可计算得到ms作为双相机系统的三维坐标测量准确度的表征量。推理并得到，点位偏差的均方根值σ越小，双相机的三维坐标测量准确度越高。

1.3长度测量准确度

长度测量准确度是指双相机测量系统测得长度值与被测长度值的标准值之间的一致程度。由于激光干涉仪的长度测量误差远小于被测试系统的长度测量误差，因此采用激光干涉仪的长度测量值作为标准长度代替真值。

设第i次测量中，测量长度与标准长度的差值为ΔLi，其中i=1，2，…，n，n为测量次数。将长度测量的均方根误差记为mΔL，则：

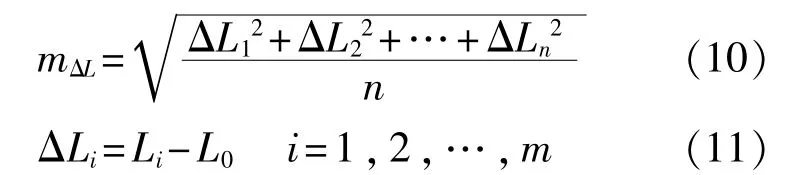
式中：Li——第i次测量时标准长度的测量值；

L0——标准长度的标称值。

由于标准长度有标定的误差，设其为mL0。由式（11）和误差合成原理可知：

因为标准长度标定的误差远小于双相机系统的测量误差，所以观测值的均方误差mΔL2近似等于相机的测量误差mL2。所以，测量中误差mΔL2的值越小，相机的长度测量准确度越高。

2　测试方案的设计与优化

根据评定的原理与指标的选择，本文将双相机系统的测量性能测评方案按下面4步进行：1）进行试验场标志点的布设；2）单相机测量；3）对双相机系统测试时的几何结构参数进行优化；4）根据评定的指标与原理进行测试。

2.1试验场的布设

测试方案的试验场测量对象选择的是一面稳定的水泥墙面，在上面均匀布设有135个编码标志点和400多个单点（见图1）。标识点均采用摄影测量系统中的回光反射标志点。

图1　试验场测试墙面

2.2单相机测量

试验场布设完成以后，在墙面上架上摄影测量基准尺，用单相机按照9点法［8］网形对墙面进行测量，得到标志点的三维坐标。为双相机测量系统的定向和三维坐标测量准确度测试提供基准。测试实验中所用单相机是郑州辰维科技自主研发的MPS/S36工业摄影测量单相机系统，点位测量误差为5 μm+ 5μm/m，测量重复性为0.020mm［9］。

2.3结构参数优化

本文结合现场测试条件，通过3个实验从3个方面对双相机系统测试时的结构参数进行优化［10］，使测试时的几何结构达到最优。

2.3.1最佳摄影距离的选择

首先根据测试墙面的长度和宽度，按照工程经验，将基线长度固定为3m。改变摄影距离，同时调整闪光灯指数，使每次拍摄标志点灰度值保持一致，并保持两台相机相对墙面中轴线对称。将测量得到标志点坐标通过公共点转换与单相机测得的标志点坐标进行对比，分析对比结果，选择最佳摄影距离。具体实验结果如图2所示。

图2　点位偏差随摄影距离的变化曲线图

可以很清晰地看到当摄影距离为2～3.5m时，双相机相对于单相机的点位偏差最小，而且变化不大，说明在此段距离内双相机点位测量准确度最高。已知被测试墙面的长度为3.3m，结合实验结论和实际工程实践，可以得到摄影距离应该近似等于或略小于被测物体长度的结论。

2.3.2最佳摄影基线长度的选择

基于实验一的结果，将摄影距离固定为3 m，改变摄影基线长度，不改变其他影响因素。分析对比结果，选择最佳摄影基线长度，实验结果如图3所示，可以看到当摄影基线长度在5～6m范围内，双相机相对于单相机的点位偏差最小，说明此时双相机点位测量准确度最高。同时可以得到，在摄影基线变化的过程中，双相机的摄影光轴的交会角也在不断地发生变化，变化区间约为20°～112°，最佳交会角在80°～90°。

图3　点位偏差随摄影基线长度的变化曲线图

2.3.3相机位置偏离检定墙中轴线距离

在实验1和实验2的结果将摄影距离固定为3m，基线长度固定为5 m，将两台相机同时向左（设为-）或向右（设为+）偏移（如图4所示），每偏移一个距离进行一次测量，将测量结果与单相机测量结果进行比对可得到图5所示结果。

图4　相机架设位置示意图

图5　点位偏差随相机位置偏离距离的变化曲线图

通过上述3个实验，可以总结得到双相机系统精度受系统几何结构（网形）变化的影响非常明显。分析上述3个结构因素，发现3个因素相互联系相互制约。首先根据被测物体大小确定摄影距离，然后根据最佳交会角度区间确定最佳基线长度，再根据2.3.3结论适当调整双相机系统的位置。根据上述原则，即使测试对象发生变化也能分析得到最佳的测试条件。

2.4测试方案设计

根据2.3中的实验结论，在对双相机系统的测量性能进行测试与评定时应该将各影响因素设置到对测量性能影响最小的条件下。具体测试条件为：摄影距离为3 m，摄影基线长度为5 m，两台相机关于墙面的中轴线对称，同时将闪光灯指数调到最佳，使标志点灰度值达到200以上且不曝光过度（本文测试时闪光灯指数设为11）。按照评定的原理，本文从以下3个方面对双相机系统进行测试评定。

1）测量重复性。在上述实验条件下，对测试墙连续测量10组数据，在MPS软件中以第1组为基准进行公共点转换，计算测量重复性。

表1　双相机系统测量重复性测试结果　mm

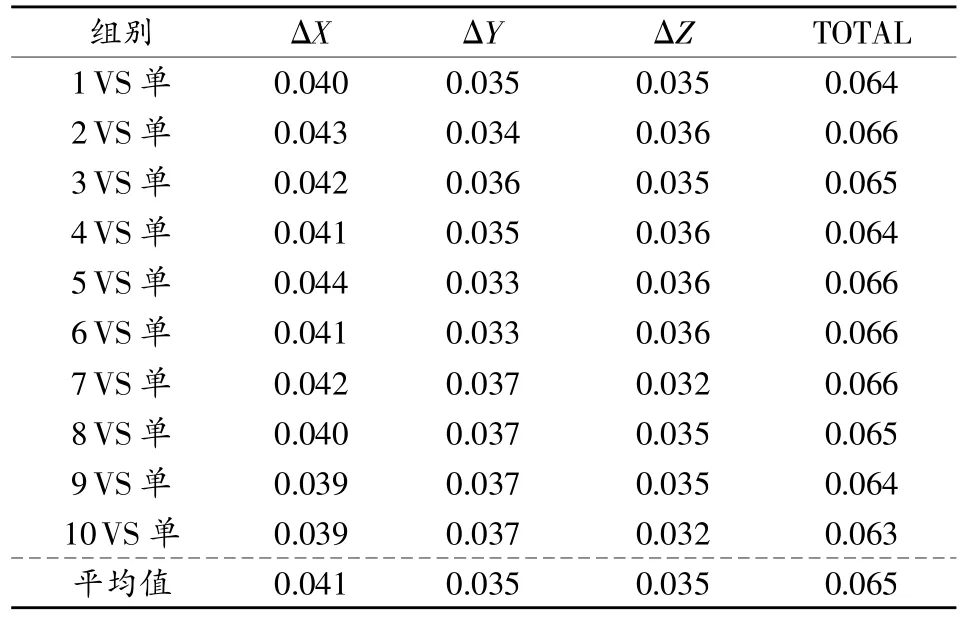
表2　双相机系统相对于单相机系统的点位偏差　mm

2）三维坐标测量准确度。在最佳测试条件下，对测试墙面进行10次测量，将得到的三维坐标以单相机系统的坐标测量结果为基准进行公共点转化，计算得到双相机系统相对单相机系统的点位偏差。

3）长度测量准确度。在最佳测试条件下，对一具有标准长度的目标（如基准尺）进行10次重复测量。已知在实验条件下标准值的标定误差为0.4μm［11］，远小于双相机的测量误差，可忽略不计，直接将双相机测量值相对标准长度的测量误差作为双相机系统的长度测量准确度的表征值。

3　可行性研究实验

按照所设计的测试方案进行可行性研究实验，并对结果进行统计。测量重复性测试实验结果见表1。由表可得，在最佳实验条件下，被测试的双相机系统的自身测量重复性为0.027mm。

双相机系统三维坐标测量准确度测试实验结果如表2所示。可以得到，双相机系统相对于单相机系统的点位偏差为0.065 mm，已知单相机在此实验条件下三维坐标测量误差为0.024mm，由式（9）可以计算得到双相机系统的三维坐标测量误差为0.060 mm，并以此评价被测试系统的三维坐标测量准确度。

双相机系统长度测量准确度测试实验结果如表3所示。由表可知，双相机在最佳实验条件下长度测量值相对于标准值的差值均方根误差平均值为0.062mm，所以双相机系统的长度测量准确度为0.062mm，并以此评价被测试系统的长度测量准确度。

表3　双相机系统标准长度测量准确度　mm

4　结束语

本文结合工程实际应用的需求，根据准确度评定原理，提出以测量重复性、三维坐标测量准确度、长度测量准确度为评价指标的双相机系统测量性能的测评方法。测量重复性能够很直观地评价系统自身的稳定性，三维坐标测量准确度与长度测量准确度则分别基于不同的外部标准对双相机的测量准确度进行了直观准确地外部检核与评价。从测试方案的可行性研究实验结果可以看出，该方法能够快速准确地给出双相机测量性能的评价的结果，为双相机系统相关检定规范的制定和应用提供了良好的基础。

［1］冯其强，李广云，李宗春.数字工业摄影测量技术及应用［M］.北京：测绘出版社，2013：2-5.

［2］张建新，段发阶.用于三维尺寸检测的双目视觉传感器［J］.计量学报，1999，20（2）：96-100.

［3］黄桂平.数字近景工业摄影测量关键技术研究与应用［D］.天津：天津大学，2005.

［4］于英.双目动态摄影测量技术研究与实现［D］.郑州：解放军信息工程大学，2010.

［5］刘亚菲，郭慧，聂冬金，等.双目立体视觉系统测量精度的分析［J］.东华大学学报（自然科学版），2012，38（5）：572-576.

［6］GUOYB，YAO Y，DI X G.Researchon structural parameteroptimizationofbinocularvisionmeasuring system for parallel mechanism［J］.IEEE International Con ference on Mechatronics&Automation，2006，6（2）：1131-1135.

［7］倪育才.实用测量不确定度评定［M］.北京：中国质检出版社，2014：13-14.

［8］黄桂平，王伟峰，轩亚兵，等.工业摄影测量系统检定方法研究进展［J］.中国测试，2015，41（7）：10-15.

［9］轩亚兵，王伟峰，高亚伟，等.国产工业摄影测量相机精度测评［J］.宇航计测技术，2015，35（4）：14-18.

［10］刘俸材，谢明红，颜国霖.双目立体视觉系统的精度分析［J］.计算机工程，2011，37（19）：280-285.

［11］甘晓川，赫明钊，李连福，等.一种摄影测量基准尺的校准方法及不确定性分析［J］.计量学报，2012（5）：33-37.

（编辑：李刚）

Study on measurement performance test method of dual camera industrial photogrammetry system

HUANG Guiping1，2，XUAN Yabing1，MA Tongtong1
（1.North China University of Water Resources and Electric Power，Zhengzhou 450045，China；2.Chenwei Technology Co.，Ltd.，Zhengzhou 450001，China）

The measurement performance of dual camera industrial photogrammetry system has attracted increasingly wide attentions.How to evaluate its measurement performance precisely and rationally and make a corresponding verification specification are current problems demanding prompt solution.A systematic method has been proposed to test the measurement performance of the dual camera industrial photogrammetry system：Firstly，the structural parameters such as shooting distance and baseline length were analyzed and the best results among them chosen to test the measurement performance of the system.Secondly，the measurement repeatability，the 3D coordinate measurement accuracy and the length measurement accuracy were tested and evaluated.Thirdly，the measurement performance was analyzed and evaluated through the three indicators above in general.The experimental results show that the measurement repeatability of the dual camera is 0.027mm，the 3D coordinate measuring accuracy is 0.060mm，and the length measurement accuracy is 0.062mm.It is recommended that the accuracy of the system is evaluated by three indexes，which are the measurement repeatability，the 3D coordinate measurement accuracy，and the length measurement accuracy.

dual camera；industrial photogrammetry；repeated measurement accuracy；coordinate measurement；length measurement

A

1674-5124（2016）05-0006-05

10.11857/j.issn.1674-5124.2016.05.002

2015-11-07；

2016-01-19

黄桂平（1973-），男，江苏常州市人，副教授，博士，研究方向为工程与工业摄影测量。