银行信贷、房地产价格与经济增长的非线性关系研究

段进+曾琦+张乐天

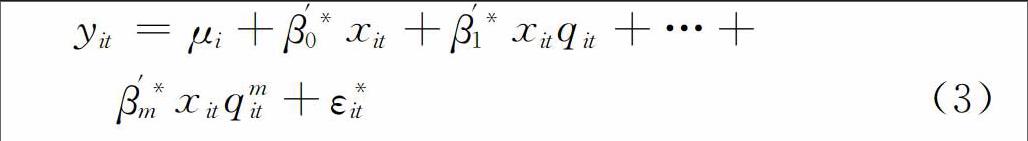
摘要：选用中国2000～2014年31个省的面板数据，以银行信贷为转换变量，通过构建面板平滑转换模型对我国房地产价格与经济增长的非线性关系进行考察。研究发现：当信贷增长率低于28.74% 时，房价增长率对经济增长产生比较显著的正向影响；当信贷增长率高于28.74%时，房价增长率对经济增长起到了明显的阻碍作用。因此，为了实现“稳定房价和保持经济平稳增长”的目标，央行应将信贷增速维持在低增长体制的最优区间中。同时，央行还应该改善信贷结构，鼓励和引导金融资源进行合理配置。

关键词： 房地产价格；银行信贷；经济增长；面板平滑转换模型

中图分类号：F830.572 文献标识码： A 文章编号：1003-7217（2016）04-0018-07

一、引 言

房地产业横跨生产、流通、消费三大领域，是我国的支柱产业和先导产业，在国民经济中具有重要的地位。房地产业不仅对于经济发展具有高度的敏感性和超前性，成为极为重要的经济增长点，而且与人民的生活也息息相关。中国自1998年实施住房货币化改革以来，大量银行信贷资金以住房消费贷款、房地产开发贷款、土地储备贷款等多种形式流入房地产市场，金融支持下的房地产市场获得了空前的繁荣，成为推动我国经济持续高速增长的重要因素。然而，由于房地产市场机制不完善、供需失衡等多种因素影响，我国房地产市场呈现出较大的区域性差异，一线城市房地产价格上涨过快，不得不实行限购；但与此同时，三、四线城市却房屋库存严重，使得以往促进经济增长的引擎失去了动力。为了应对经济下滑并化解房屋库存，我国从2015年1月～2016年3月期间共6次降低法定存款准备金率，5次降低金融机构人民币贷款利率，2次降低二套房贷款首付比例，多重直接或间接放松银行信贷的政策是否会促使房价再次上涨，从而对宏观经济的稳定造成威胁？银行信贷、房价波动与经济增长之间的相互作用机制如何？尝试回答这些问题成为本文研究的主要目标。

二、文献综述

关于房地产价格与经济增长的实证研究，一直是国内外学者研究的热点。然而，对于“房地产价格如何影响经济增长”，学者们并未达成广泛的共识，形成了以下几种观点：第一种认为，房地产价格的上涨对经济增长有显著的促进作用。Chirinko，De Haant and Sterken（2004）研究发现，如果房价上涨1.5个百分点，生产总值将上涨0.4个百分点[1]。崔光灿（2009）的研究认为，房地产价格明显影响到宏观经济的稳定，房地产价格上升会增加社会总投资和总消费，房地产投资通过“财富效应”对消费的影响始终明显，对社会总投资的影响也非常显著，因此促进经济增长[2]。高东胜（2011）指出，在短期内房价上涨对我国经济增长的拉动作用十分明显[3]。杨俊杰（2012）实证检验了房地产价格波动对宏观经济波动的作用机制，认为房地产价格的正向冲击对GDP具有快速拉升作用[4]。第二种认为，房地产价格过度上涨对经济增长有负面影响或影响不显著。Gelain、Lansing 和Mendicino（2013）研究发现，房价偏离宏观经济的过度上涨会通过影响公司和投资者对价格信号的反应，导致资本没有得到合理配置而对经济产生不利的影响[5]。孔煜（2009）实证分析表明，过度的金融支持使东中部地区的房价偏离了经济基本面，成为阻碍经济增长的隐患[6]。王擎、韩鑫韬（2009）发现房价波动以及房价与货币供应量的联动会显著导致GDP增长率的下降，但房价的波动对经济增长的波动没有显著影响[7]。第三种认为，房地产价格上涨对经济增长的影响可能是非线性的。沈悦和刘洪玉（2002）对我国房地产价格与城市经济指标的相关性进行了分析，认为保持适度的房地产价格上涨速度，对于宏观经济的发展能够起到一定的促进作用，一旦价格增长过快，超过国民经济和社会发展的承受能力和消化能力，将带来非常严重的后果[8]。段忠东（2012）运用非线性的门限自回归模型刻画了房价与未来通胀与产出的非线性关系，结果发现，房价与产出存在一个房价增长率门限效应，当房价处于低增长阶段时，房价增长率对于产出有比较显著的正向影响；而当房价处于高增长时期，房价实际增长率对产出的影响效果不显著[9]。

国内外学者在房地产价格与经济增长波动关系的研究方面取得了一定的成果，但是，现有研究中较少从银行信贷的角度去分析房价波动如何影响经济增长。发掘银行信贷冲击影响房地产价格的内在机理，将是深入研究房地产价格与经济增长关系的重要突破口。Hofman（2003）认为将银行信贷因素纳入房地产价格模型的研究是十分有必要的，银行信贷因素的冲击会对房地产价格产生明显的正向影响[10]。Iacoviello（2005）在一般均衡分析框架下分析信贷约束、房地产价格和经济周期的互动影响，结果发现信贷约束和房地产价格的互动反馈使经济冲击的影响被不断放大和扩散[11]。Jarociński和 Smets（2008）对英国经济周期中的住房投资和房价进行了研究，结果表明货币政策是引起住房投资增加和房价上涨的重要原因[12]。Chen、Chou和Wu（2013）研究发现，银行信贷的冲击对房价的影响是非线性的。在低增长体制下，房价对银行信贷冲击的反应比在高增长体制下更强烈[13]。Baldi（2014）在研究央行的货币政策对房价反应的经济效应时，认为央行如果不控制投入房地产的信贷资金总量，则房价上涨会更加明显[14]。

综上所述，国内外学者在研究银行信贷、房地产价格与经济增长的关系时，大多集中在研究其中两个变量之间的关系上，而将三个变量置于模型中进行研究的较少；大多数研究忽视了房地产价格不同程度的上涨可能会诱致经济增长出现非线性的机制转换，房地产价格与经济增长的关系并不是简单的线性关系，这也导致了以前研究的结论存在较大分歧。鉴于此，本文试图建立面板平滑转换模型研究房地产价格与经济增长的非线性关系，并将对房地产价格影响较大的银行信贷作为转换变量纳入模型的分析框架进行实证检验。

三、理论分析

银行信贷作为国民经济的资金纽带，为各行各业的高速发展提供了金融支持。长期以来，我国房地产企业的资金高度依赖于银行信贷，房地产行业所取得的成就与银行信贷的支持与配合是密不可分的。银行信贷投向房地产的资金主要包括房地产开发投资资金以及个人住房按揭贷款。2000～2015年房地产投资中直接来源于银行信贷的比例最低为22.7%，最高为53.2%。另外，银行信贷还会借助理财产品、房地产信托产品、民间借贷等影子银行通道间接流入房地产市场。实际上，银行信贷投向房地产市场的这一比例会更高。正是因为银行信贷的支持与配合，在一定程度上推动了我国房地产价格的持续上涨。

在复杂的现实经济环境中，银行信贷、房地产价格与经济增长的关系更可能表现为非线性动态的特征。宽松的银行信贷政策推动了房地产价格的持续上涨，房价的上涨又主要通过消费和投资两个途径对经济增长产生影响，由于投资和储蓄是此消彼长的关系，故投资与储蓄的对比决定了房价对产出的影响方向和力度。因此，可以将不同信贷增速下，房地产价格对经济增长的影响分为两个阶段来讨论：

第一阶段，信贷规模在低增长体制中，房价处于温和上涨的阶段，房价上涨对总需求起到稳定的正向推动作用。（1）信贷扩张，房价温和上涨。由于房屋存量资产不足和融资约束的存在，当银行信贷扩张时，房地产企业融资成本下降，这在一定程度上使房地产行业整体投资门槛降低，引起市场投资需求的增加从而吸引更多的资金流入到房地产市场中。对消费者而言，在宽松的信贷政策和快速城市化进程的推动下，越来越多的中低收入家庭通过个人住房抵押贷款加入到购房的行列，增加了对住房的需求量。此时市场上需求大于供给，房地产价格上涨。（2）随着房价的上涨，房地产行业的繁荣必将带动相关上下游行业的高速发展，促使整个社会的投资稳定增长。同时，房产财富效应①逐渐显现出来，房价上涨的预防性储蓄效应②逐渐减弱，住房资产的增值使房屋所有者的租金收入、房屋转让收入和住宅抵押贷款收入上升，从而带动房产所有者增加消费。在这一阶段，投资大于储蓄，所以房价对总需求起到稳定的正向推动作用，经济高速增长。

第二阶段，信贷规模在高增长体制中，房价处于高速上涨的阶段，房价对经济增长的推动作用减弱或阻碍经济增长。（1）银行信贷进一步扩张，房价泡沫日益突显[15，16]。房地产业高额的投资收益和消费者形成的房价将持续上涨的非理性预期，会扩大房地产开发商和住房消费者对银行的贷款需求。而对银行来说，房地产作为银行一种重要的贷款抵押品，在房价上涨的情况下，银行所拥有的抵押物的价值上升，银行自身的资金质量和整体财务情况得到改善，也会更加倾向于提高贷款额度，从而进一步扩大贷款规模[18，19]。由此将进一步推动房地产价格上涨，使房地产市场走向非理性繁荣。（2）在这一阶段，融资约束逐渐弱化至零，房地产市场投资超过一定的规模出现过热时，房地产市场的消费需求和投机需求由于过高的价格、预期转变或者其他因素影响而难以继续增长甚至出现下降。市场供求的不平衡导致房屋存量急速增加、新建房屋空置率较高，房价上涨对投资的刺激作用受到反向抑制而开始弱化；同时，伴随着房价的快速上涨，居民预防性储蓄和负收入效应快速增强，房价对消费的促进作用逐渐减弱，或者可能出现房价高涨对消费的挤出。当银行信贷扩张过度，使得房价脱离基础价值快速上升至泡沫阶段，房地产业将吸纳社会资本长期停留进行投资和投机活动，使实体经济中其他行业可用资金变少，这也会降低实际产出和总产出[9]。因此，房价对产出的边际影响可能会出现两种情况：一是房价对产出的边际影响为正，但影响力度较小或不显著；二是出现储蓄大于投资的极端情况，房价对产出产生抑制作用，阻碍经济增长。

四、经验模型与变量选取

（一）模型设定与估计方法

面板平滑转换模型（Panel Smooth Transition Regression Models，简称PSTR模型）是一个非线性面板数据模型，最早由González、Tersvirta and Dijk（2004）提出，该模型能够较好地处理异质面板数据，这种异质性主要是指模型的系数可以随时间与截面的变化而变化，这种变化主要是通过转换函数在不同的体制之间平滑转换来完成[19]。该模型改进了Hansen（1999）面板门限回归模型（PTR）从一种体制突变为另一种体制的严格假设，使不同体制的转换变为一个连续的平滑过程，更贴近于经济现实[20]。实际上，面板平滑转换模型是面板门限回归模型的一般形式。基本的PSTR模型如下：

（二）变量选取与数据说明

本文采用我国31个省市2000～2014年的年度面板数据，数据样本以1999年为基期剔除了通货膨胀的因素。所有的数据来源于《中国统计年鉴》、《中国金融年鉴》和wind数据库。各变量的代理变量选取如下：（1）被解释变量：经济增长率（ggdpit）采用各省市的实际GDP增长率衡量。（2）解释变量：房价增长率（hpit）采用各省市住宅商品房的实际价格增长率作为代理变量。（3）转换变量：信贷增长率（loansit）采用各省市全部金融机构各项贷款余额的实际增长率来衡量。（4）控制变量：消费增长率（consumeit）采用各省市消费总量的实际增长率来衡量。其中，消费总量不仅包括居民的消费，还包括政府的消费即政府购买。净出口增长率（netexportit）采用各省市净出口的实际增长率来衡量。投资增长率（investmentit）采用各省市全社会固定投资的实际增长率作为代理变量。

五、实证分析

（一）Hausman检验

在处理面板数据时，究竟使用固定效应还是随机效应模型是一个基本的问题。为此，采用Hausman检验来确定模型的形式。希望检验原假设：随机效应模型为正确模型，Hausman检验显示F检验统计量为18.29，p值为0.0026，说明强烈拒绝原假设，应该使用固定效应模型。

（二）面板单位根检验

本文的数据为面板数据，有可能存在不平稳问题，会使得回归结果出现偏差和不一致。为了避免伪回归现象，采用LLC和FisherADF检验方法对各变量进行单位根检验，发现在5%的显著性水平下，所有变量均可以拒绝存在单位根的原假设，即所有变量均为平稳序列。

（三）模型的非线性检验

在估计面板平滑转换模型之前，首先必须对假设方程进行非线性检验，确定其是否存在异质性。但由于模型中含有未识别的参数γ，c，所以，不能直接对模型进行非线性检验。本文借鉴Golletaz，Hurlin的做法，将转换函数g（qit；γ，c）在γ=0处一阶泰勒展开，得到辅助回归方程：

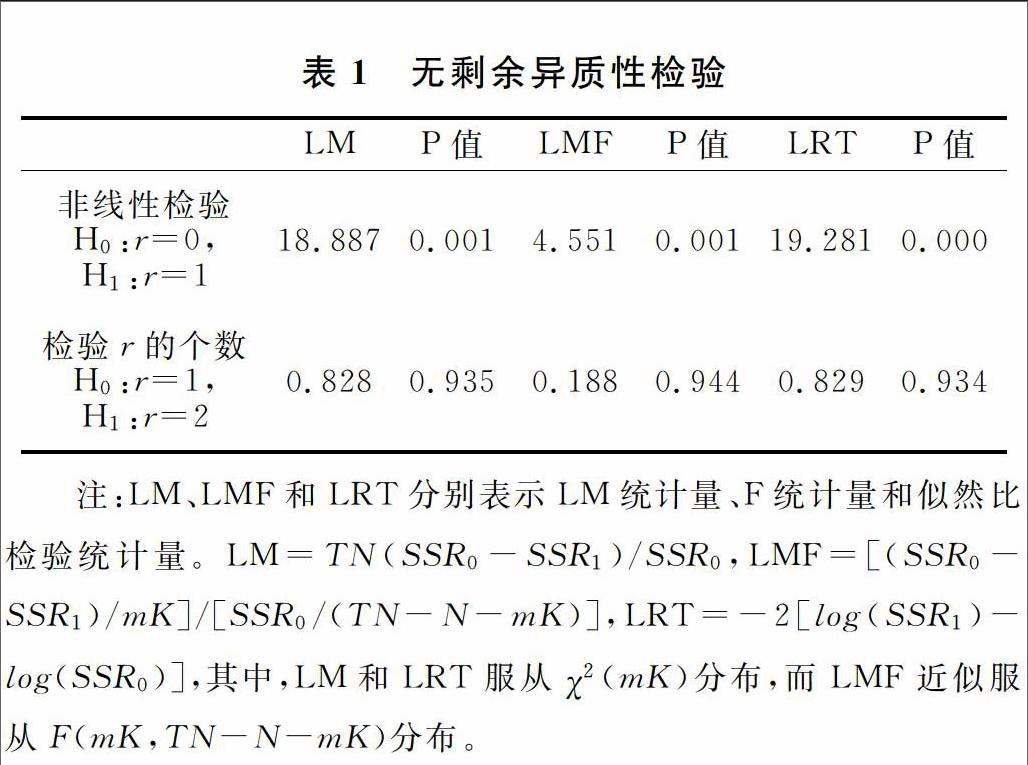
在辅助回归方程中，检验假设H*0：β′*1=…=β′*m=0，然后将辅助回归方程所估计的残差平方和与线性固定效应所估计的残差平方和，联合构造统计量对原假设进行检验，如果拒绝原假设，表示模型具有非线性关系。在确定了非线性关系后，要对模型进行“无剩余异质性检验”，进一步确定模型中转换函数的个数。在实际检验过程中，首先对原假设H0：r=r*以及相应的备择假设H1：r=r*+1进行检验，如果拒绝原假设H0，则继续对H0：r=r*+1以及相应的备择假设H1：r=r*+2进行检验，依次类推，直到无法拒绝原假设H0为止。

由表1的检验结果可知，当银行信贷作为转换变量对房地产价格与经济增长之间的关系进行非线性检验，LM、LMF与LRT检验统计量的P值分别为0.001、0.001和0.000，显著地拒绝了两者为线性关系的原假设。这表明面板数据存在异质性，使用银行信贷作为转换变量能够较好地捕捉房地产价格与经济增长的非线性关系。接着，进行“无剩余异质性检验”以考察PSTR模型中转换函数（体制转换区间）的最优个数。由表1的结果分析可得，三个检验统计量p值均较大，无法拒绝H0：r=1的原假设，所以本文用到的模型中，非线性转换函数的最优个数应为1。

接下来，利用AIC与BIC准则选择适当的位置参数的个数，表2结果显示转换变量loansit的最优位置参数个数为1。

（四）模型的参数估计

采用González、Tersvirta and Dijk（2004）提出的网格点搜索法进行参数估计，首先通过去均值的方式消除固定效应，然后用网格点搜索的方式得到使模型残差平方和最小时所对应的参数γ、c，即为最优的参数估计。确定了平滑参数和位置参数后，最后运用非线性最小二乘法（NLS）估计模型[19]。上述方法具体的实现通过MATLAB7.11.0编程完成，得到各参数的结果见表3。

2.房地产价格对经济增长的影响。从表3和图2可以看出，房地产价格与经济增长的关系因银行信贷增速的不同而呈现出显著的变化。由于模型只有一个转换函数，对应一个位置参数，所以，该模型是一个两体制模型。当信贷增长处于低体制状态下（loansit≤28.74%），房地产价格上涨对经济增长的影响系数为0.1063，并且在1%的显著性水平下显著；当信贷增长处于高体制状态下（loansit>28.74%），房地产价格影响经济增长的系数突变为-0.0022，在5%的显著性水平下显著。这意味着银行信贷控制在一定的范围时，房地产价格的上涨有利于促进经济增长；而随着银行信贷的扩张，房价也随之上涨，一旦信贷增长率超过28.74%，房地产价格的持续高速上涨将显著地阻碍经济增长。这一结论与我国近年来的实际情况基本上是一致的。这是因为房地产产业具有关联度强、带动系数大的特点，房地产业的正常发展，能够拉动上下游如钢铁、建材、机械、化工、纺织、家电、家具等一系列产业的发展，但当其价格太高成为投机品后，则会形成大量的空置房或房屋库存，这样会产生两方面的负作用：一是积压和占用了大量金融资源，使金融资源不能得到有效配置；另一方面是空置房和库存房不能有效带动其他行业的发展。在这种情况下，房地产价格不仅没有拉动经济增长，反而对宏观经济产生了负面影响。3.控制变量对经济增长的影响。当信贷增长率从低于28.74%的低体制状态转变为高体制状态时，控制变量也发生了相应的变化。（1）消费增长率（consumeit）对经济增长的影响系数由0.2003变为0.1593，消费对经济增长的促进作用有所减弱。原因是房价上涨一方面吸引居民将资金投向房地产市场进行投资投机活动从而减少消费，另一方面由于流动性约束效应的存在，房价上涨导致消费者为购房而增加储蓄，降低消费。（2）在信贷增速处于不同的体制下，投资（investmentit）对经济增长的影响系数由0.1564突变为0.0830，尽管系数都为正，但前后的影响力度发生了较大的变化。由于全社会固定资产投资中房地产投资占比较大，房地产过度积压金融资源使实体经济中其他投资项目可用资金变少，这在一定程度上削弱了投资对经济增长的拉动作用。（3）净出口（netexportit）对经济增长的影响系数由-0.0005变为0.0012，尽管在统计意义上是显著的，但影响力度很小。

（五）稳定性检验

通过改变样本容量，采用2000～2012年、2000～2013年、2000～2014年的数据分别进行实证检验，求出的门槛值分别为0.2868、0.2872、0.2874。可见，2000年至最近三年期间门槛值趋于稳定，表明门槛值具有较好的持续性。由于本文的转换变量为银行信贷，当银行信贷受政策等因素影响时，门槛值也会发生变化，但总体来说是稳定的，能较好地解释房地产价格与经济增长的非线性关系。

六、结论与政策建议

以上基于我国31个省市2000～2014年的年度面板数据，以银行信贷增长率为转换变量，运用面板平滑转换模型考察了我国房地产价格与经济增长之间的非线性关系。结论显示：我国房地产价格与经济增长之间的关系存在非线性的信贷增长率门限效应，信贷增长率的门槛值为28.74%。这意味着银行信贷是影响我国房地产价格与经济增长关系的一个重要因素。当信贷增长率处于低于28.74%的低体制状态时，房地产价格上涨对经济增长有显著的促进作用；而当信贷增长率高28.74%处于高体制状态时，房地产价格上涨对经济增长的影响系数为负，表明信贷增长率过高引发的房地产泡沫将阻碍经济增长。

我国经济正处在增速换挡和转变发展方式的阶段，经济结构调整的阵痛与四万亿投资的后遗症交织，经济增长引擎减弱与房地产价格泡沫的问题并存，因此，我国要维持房地产价格稳定，防止房地产价格的大幅度波动对经济产生不利影响，重点是央行调控好信贷增速。在房地产市场泡沫膨胀的阶段，可采取稳中偏紧的货币政策，抑制房地产市场泡沫的进一步扩大，引导房地产价格逐步回归理性状态，控制经济风险；在房地产市场成交低迷、房价增速放缓的阶段，为了实现经济平稳增长的目标，央行即便采取宽松的信贷政策，也应控制好力度，将信贷增长率控制在低于28.74%的最优区间内。

央行的货币政策除了要控制好信贷增速外，还应该坚持“总量稳定、结构优化”的取向。盘活存量，优化增量，改善融资结构和信贷结构，鼓励和引导金融机构更多地将信贷资源配置到经济生活中的重点领域和薄弱环节，防止房地产业过多地积压和占用银行的信贷资金，造成银行信贷资金对实体经济其他领域支持不足的现象。

注释：

①Ludwing和Slock（2002）[21]将“房产财富效应”细分为“兑现的财富效应”与“未兑现的财富效应”两种：前者指住房资产的增值使房屋所有者的租金收入、房屋转让收入或住宅抵押贷款收入上升，从而带动房产所有者消费的上升；后者指房产财富一定程度上代表房屋所有者的“持久收入”，房产价格上升时，房产财富的价值上升，房屋所有者会因“持久收入”增加而消费。

②房价的预防性储蓄效应：房地产价格的上涨会促使租房者和潜在购房者为买房进行更多的储蓄，降低当期消费。

③是本文解释变量hpit在低体制下的系数β01，其余解释变量类似。

④是本文解释变量hpit在高体制下的系数，由β01+β11g（loansit；γ，c）计算得出，其余解释变量在高体制下的系数类似计算。

⑤Fouquau et al.（2008）[22]、Omay和kan（2010）[23]、Delatte和Fouquau（2011）[24]等人指出，面板平滑转换回归模型（PSTR）是面板门限回归模型（PTR）的普遍化形式，即面板门限回归模型仅为面板平滑转换回归模型的一种特例，当平滑参数较大时，面板平滑转换回归模型则转变为面板门限回归模型。

参考文献：

[1]Chirinko R S， L De Haan， E Sterken . Asset price shocks， real expenditures， and financial structure： a multicountry analysis[D].University of Groningen， 2004.

[2]崔光灿. 房地产价格与宏观经济互动关系实证研究基于我国31个省份面板数据分析[J]. 经济理论与经济管理，2009，（1）：57-62.

[3]高东胜. 我国房地产价格波动的宏观经济效应研究[J]. 统计与决策，2011，（19）：116-119.

[4]杨俊杰. 房地产价格波动对宏观经济波动的微观作用机制探究[J]. 经济研究，2012，（S1）：117-127.

[5]Gelain， P. ， K. J. Lansing， and C. Mendicino. House Prices， Credit growth， and excess volatility：implications for monetary and macroprudential policy[J]. International Journal of Central Banking， 2013， （9）： 219-268.

[6]孔煜. 房价波动、银行信贷与经济增长[J]. 财经理论与实践，2009，（5）：12-16.

[7]王擎，韩鑫韬. 货币政策能盯住资产价格吗？来自中国房地产市场的证据[J]. 金融研究，2009，（8）：114-123.

[8]沈悦，刘洪玉. 房地产价格与宏观经济指标关系的研究[J]. 价格理论与实践，2002，（8）：20-22.

[9]段忠东. 房地产价格与通货膨胀、产出的非线性关系基于门限模型的实证研究[J]. 金融研究，2012，（8）：84-96.

[10]Hofmann B. Bank lending and property prices： Some international evidence[R]. HKIMR Working Paper ， 2003， （22）.

[11]Iacoviello M. House Prices， borrowing constraints and monetary Policy in the business cycle[J]. The American Economic Review， 2005， （95）： 739-764.

[12]Jarociński M， F Smets. House prices and the stance of monetary policy[R]. ECB Working Paper （European Central Bank）， 2008， No.891.

[13]Chen N K，Y H Chou， J L Wu. Credit constraint and the asymmetric monetary policy effect on house prices[J] . Pacific Economic Review， 2013， （18）： 431-455.

[14]Baldi G. The economic effects of a central bank reacting to house price inflation[J]. Journal of Housing Economics， 2014， （26）： 119-125.

[15]袁志刚， 樊潇彦. 房地产市场理性泡沫分析[J]. 经济研究，2003，（3） ：34-43.

[16]周京奎. 房地产泡沫生成与演化基于金融支持过度假说的一种解释[J]. 财贸经济，2006，（5） ：3-10.

[17]Davis E P， H Zhu . Bank lending and commercial property cycles： some crosscountry evidence [J]. BIS Working Papers ， 2004，（150）：1-37.

[18]Stefan G， W Peng.Bank lending and property prices in Hong Kong[J]. Journal of Banking & Finance， 2005，（29）：461-481.

[19]González A， T Tersvirta，D Dijk. Panel smooth transition regression model and an application to investment under credit constraints[R]. Working Paper of Stockholm School of Economics， 2004.

[20]Hansen B E.Threshold Effects in Nondynamic Panels： Estimation， Testing， and Inference[J]. Journal of Econometrics， 1999， （93）：345-368.

[21]Ludwing A， T Slok. The Impact of Changes in Stock Prices and House Prices on Consumption in OECD Countries[R]. IMF Working Paper ，2002，No.1.

[22]Fouquau J， Hurlin C， Rabaud I. The FeldsteinHorioka puzzle： a panel smooth transition regression approach[J]. Economic Modelling， 2008， 25（2）： 284-299.

[23]Omay T， znur Kan E. Reexamining the threshold effects in the inflationgrowth nexus with crosssectionally dependent nonlinear panel： Evidence from six industrialized economies[J]. Economic Modelling， 2010， 27（5）： 996-1005.

[24]Delatte A L，Fouquau J. The determinants of international reserves in the emerging countries： a nonlinear approach[J]. Applied Economics， 2011， 43（28）： 4179-4192.

（责任编辑：宁晓青）

Abstract：Based on China's 31 province-level panel data from 2000 to 2013， setting bank credit as the transition variable and applying the Panel Smooth Transition Regression Model， this paper investigates the nonlinear relationship between house price and economic growth in China. The results indicate that the effects of house price on economic growth change over the level of bank credit rate. Housing price is positively correlated with economic growth when bank credit rate below the threshold 28.72%； while bank credit rate is above the threshold， housing price is negatively correlated with economic growth. Thus， in order to realize the target of stabilizing housing price and maintaining stable economic growth， the policy authorities will not only have to keep the increasing speed of bank credit to low growth stage， but also optimizing the credit structure and allocation of financial resources rationally.

Key words：Housing price； Bank credit； Economic growth； Panel smooth transition regression model