具有无穷时滞和反馈控制的离散互惠系统的持久性

张杰华，余胜斌

（阳光学院 基础教研部，福建 福州　350015）

具有无穷时滞和反馈控制的离散互惠系统的持久性

张杰华，余胜斌

（阳光学院 基础教研部，福建 福州350015）

提出并研究具有无穷时滞和反馈控制变量的离散互惠系统模型，通过运用差分不等式得到保证该系统持久的一组充分条件。

离散；持久性；无穷时滞；反馈控制；互惠系统

得到了一组保证该系统持久的充分性条件。考虑到生态系统一直受到外界的干扰，如人类的开发等因素，则必须研究具有反馈控制的模型，如Chen［2］就研究了如式（2）单种群反馈控制模型的持久性问题

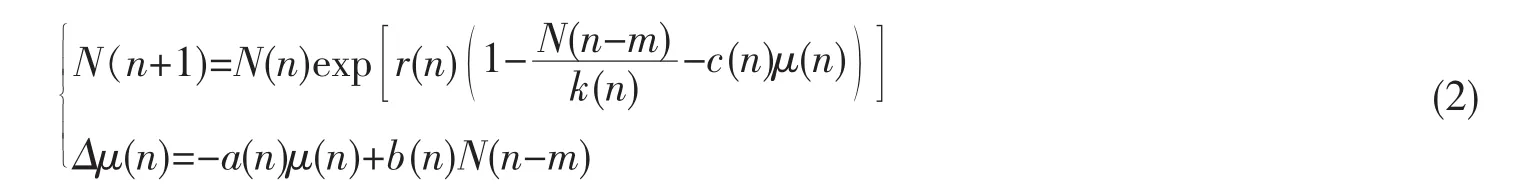
据笔者所知，尚未有学者针对模型［1］提出差分反馈控制模型，因此研究如式（3）模型

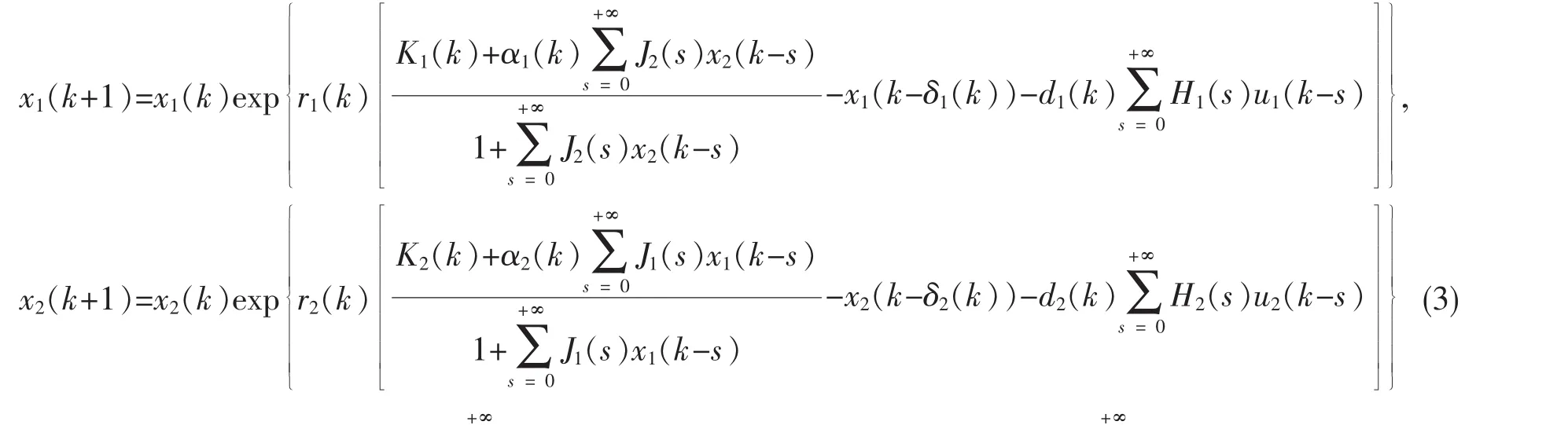
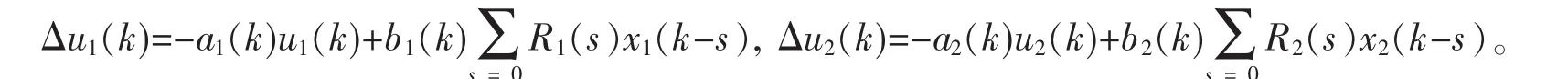
其中xi（k）（i=1，2）是第i个种群密度，ui（k）（i=1，2）是控制变量，且满足下列条件：

（H1）ri，Ki，αi，δi，Ji，Hi，Ri，ai和bi，i=1，2是非负的有正的上下界的序列，

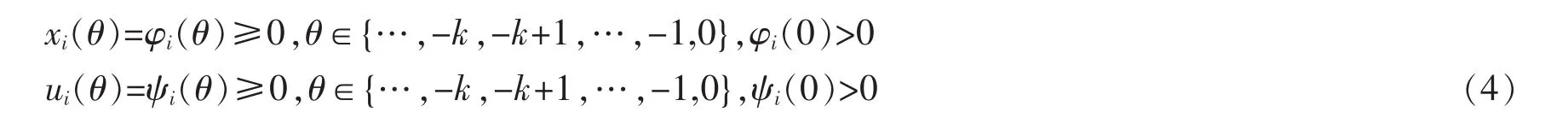
易知系统（3）满足初始条件（4）的解对任意k∈N均有定义且是恒正的。本文通过文献［2-3］的分析手法来探讨系统（3）的持久性。

1　相关引理

引理1［3］假设序列｛x（k）｝满足x（k）＞0，a（k），b（k）均为有正的上下界的非负序列，若x（k+1）≤x（k）exp｛a（k）-b（k）x（k）｝，k∈N，则

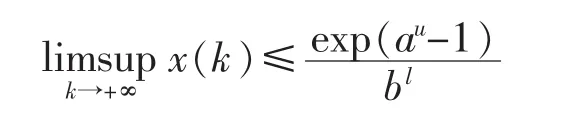
引理2［4］假设序列｛x（k）｝满足，且x（N0）＞0，N0∈N，其中a为常数且满足ax*＞1，则

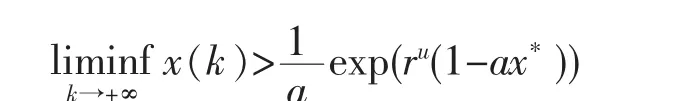
引理3［5］设x：Z→R是非负有界序列，J：N→R是非负序列，且，则

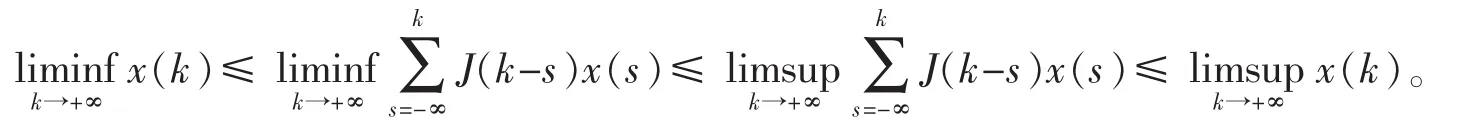
引理4［7］假设A＞0，且y（0）＞0，y（k+1）≤Ay（k）+B（k），k=1，2…，则有

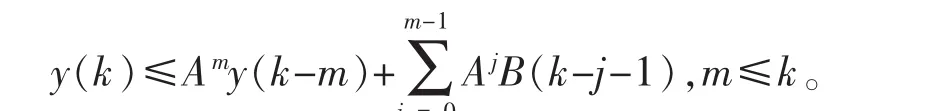
引理5［7］假设A＞0，且y（0）＞0，y（k+1）≥Ay（k）+B（k），k=1，2…，则有

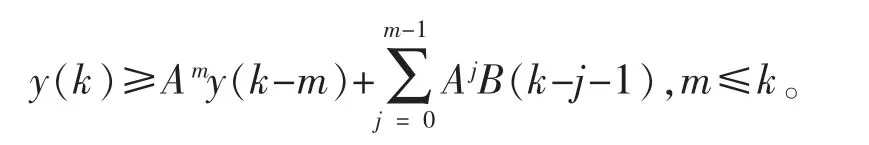
2　持久性

（H2）Kil＞diuNi

定理1若（H1）及（H2）成立，则系统（3）持久的。

证明设（x1（k），x2（k），u1（k），u2（k））T是系统（3）满足初值条件（4）的任一解。由系统（3）的前两个方程可得

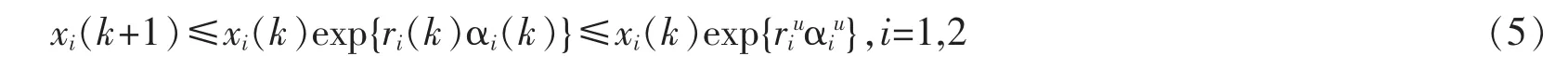
由（5）式可得

将（6）代入系统（3）的前两个方程得

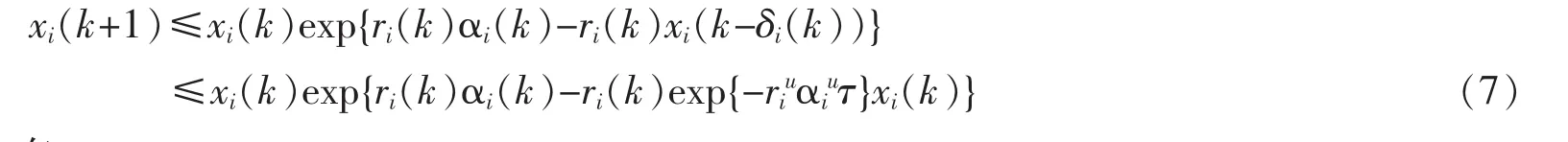
应用引理1有

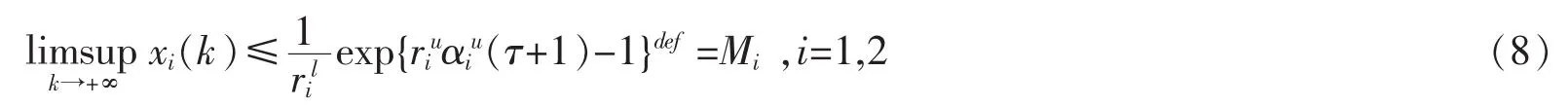
所以，由引理 3有

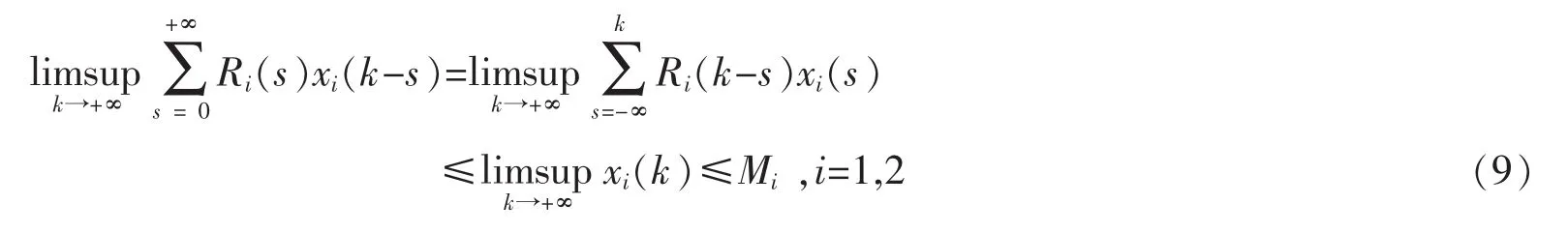
因此，对任意的ε＞0，存在T1＞0，当k≥T1时，有

将（10）代入系统（3）的第3个和第4个方程得到

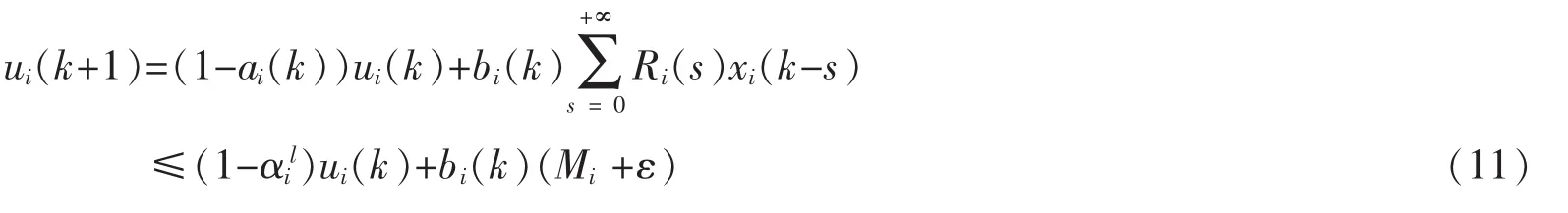
应用引理4可得

目前市场上的中药挥发油提取设备型号多样、功能各异，其质量关系到中药挥发油的质量。相关部门应尽快加强提取设备标准化管理，完善《药品生产质量管理规范》（GMP）或建立相关政策法规。由于在提取挥发油的过程中普遍存在提取工艺与提取设备不适宜的问题，因此在研发自动化、智能化挥发油提取设备的同时，必须加强提取工艺与设备的适宜性研究，从而使传统的低效、高耗能挥发油提取设备升级成高效、低耗、绿色的现代中药挥发油提取设备。

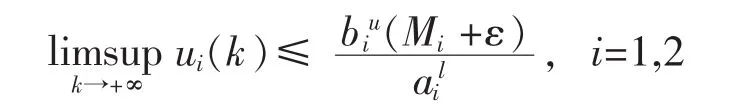
在上面的不等式中，令ε→0得到

则由引理3有

对任意的ε＞0，不失一般性，由（H2）不妨假设，由（8）和（13）式知，存在T2＞T1，使得当k≥T2时，有

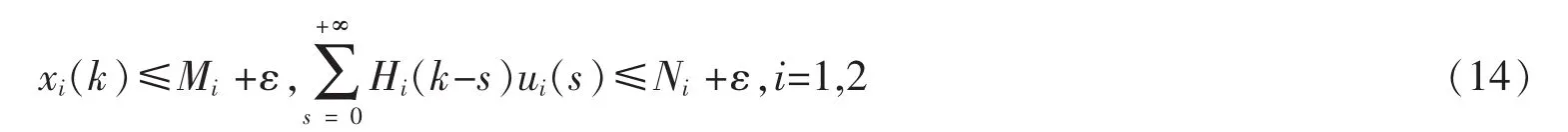
将（14）代入系统（3）的前两个方程可得，当k≥T2+τ时，

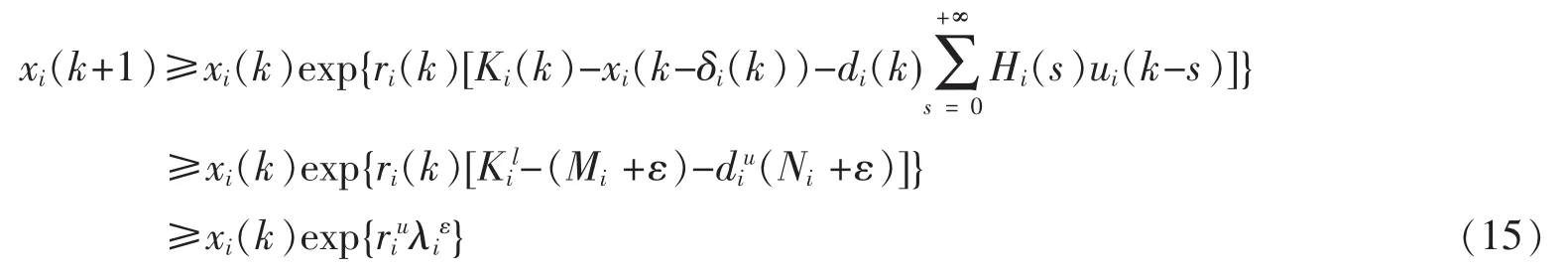
其中λiε=Kil-（Mi+ε）-diu（Ni+ε），i=1，2。显然，

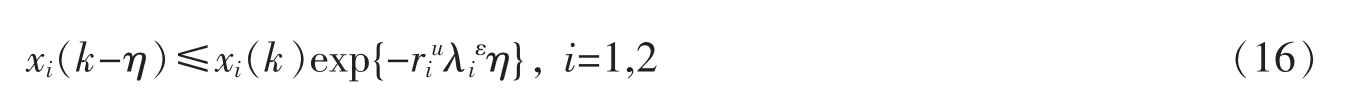
当k≥T2+τ时，将（14）和（16）式代入系统（3）的前两个方程得到

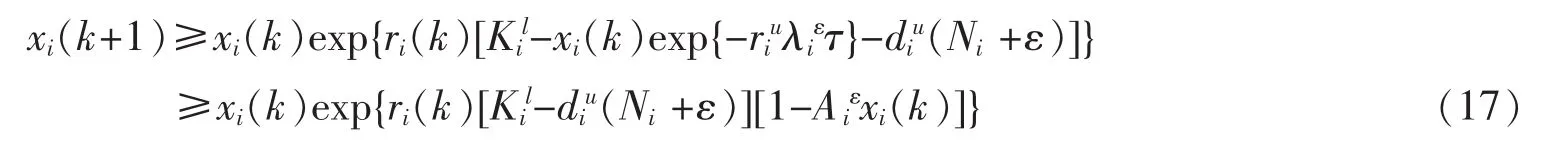
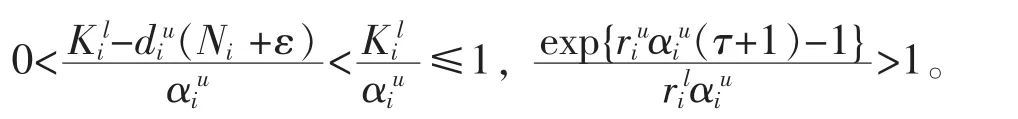
因为λiε＜0，所以

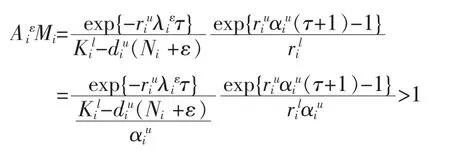
以上分析表明，如果（H2）成立，那么（17）满足引理 2的条件，由引理 2可得

令ε→0，得

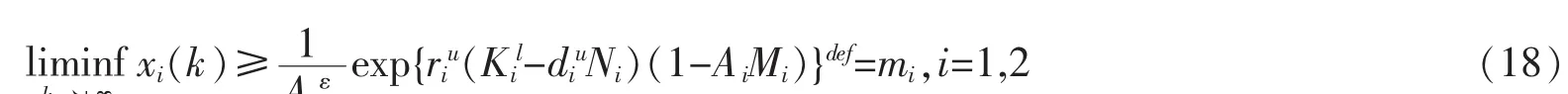
由引理3，有

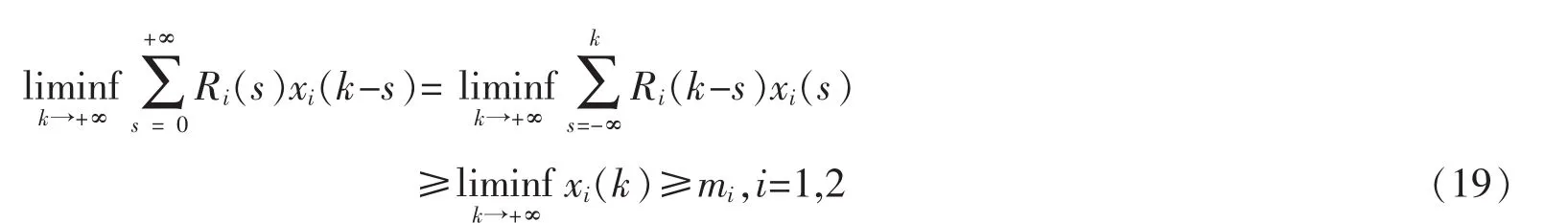
由（19）知，对任意的ε＞0，存在T3＞T2，当k＞T3时，有

将（20）代入系统（3）的第3个和第4个方程可得，当k＞T3时，

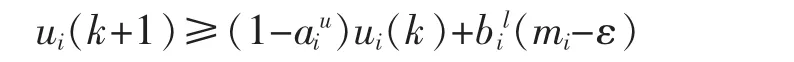
应用引理4得到i

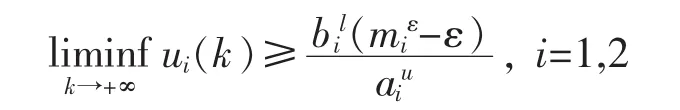
在上面的不等式中，令ε→0得到

（8），（12），（18）和（21）表明当（H1）和（H2）成立时，系统（3）是持久的。证毕。

［1］李忠.具时滞离散互惠系统的持久性［J］.数学研究，2010，43（1）：50-54.

［2］CHEN F D.Permanence of a single species discrete model with feedback control and delay［J］.Appl Math Lett，2007，20（7）：729-733.

［3］CHEN L J，LI Z.Permanence of a delayed discrete mutualism model with feedback controls［J］.Math Comput Model，2009，50：1083-1089.

［4］YANG X T.Uniform persistence and periodic solutions for a discrete predator-prey system with delays［J］.J Math Ana Appl，2006，316（1）：161-177.

［5］CHEN F D.Permanence in a discrete Lotka-Volterra competition model with deviating arguments［J］.Nonlinear Anal Real World Appl，2008，9（5）：2150-2155.

［6］XU J B，Teng Z D.Permanence for a nonautonomous discrete single-species system with delays and feedback control［J］. Appl Math Lett，2010，23：949-954.

［7］FAN Y H，WANGLL.Permanenceforadiscretemodelwithfeedbackcontrolanddelay［J］.DiscreteDynNatSoc，2008，8pages，Article ID 945109.

［8］LI Y K，Zhu L F.Existence of a positive periodic solutions for difference equations with feedback control［J］.Appl Math Lett，2005，18：61-67.

［9］余胜斌，张杰华.具时滞和反馈控制的修正Leslie-Gower离散系统的持久性［J］.应用泛函分析学报，2014，16（3）：244-249.

［10］HUO H F，LI W T.Positive periodic solutions of a class of delay differential system with feedback control［J］.Appl Math Comput，2004，148（1）：35-46.

（责任编辑：朱联九）

Permanence of a Discrete Mutualism Model with Infinite Delay and Feedback Controls

ZHANG Jie-hua，YU Sheng-bin
（Department of Basic Teaching and Research，Yango College，Fuzhou 350015，China）

In this paper，a two species discrete mutualism model with infinite delay and feedback controls is presented. Sufficient conditions which ensure the permanence of the system are obtained by difference inequality.

discrete；permanence；infinite delay；feedback controls；mutualism systems

O175.7

A

1673-4343（2016）02-0001-05

10.14098/j.cn35-1288/z.2016.02.001

2015-10-15

福建省自然科学基金项目（2015J01012，2015J01019）

张杰华，女，山东金乡人，讲师。主要研究方向：微分方程。