两个带有已知或未知参数的复杂网络的改进函数投影同步

杜洪越 李春双 公利滨



两个带有已知或未知参数的复杂网络的改进函数投影同步

杜洪越*李春双 公利滨

(哈尔滨理工大学自动化学院 哈尔滨 150080)

近年来复杂网络在科学与工程各个领域受到了广泛关注，其中复杂网络同步问题是复杂网络研究的热点之一。该文研究两个复杂网络实现改进函数投影同步的方法。分别基于复杂网络模型参数已知和未知两种情况，利用李雅普诺夫稳定性理论和自适应控制技术，设计自适应同步控制器，使两个复杂网络达到改进函数投影同步。最后分别基于这两种情况利用数值仿真验证所提方法的有效性。

复杂网络；改进函数投影同步；自适应控制；未知参数

1 引言

复杂网络是一个多学科交叉的热点研究领域，其可描述自然界和人类社会中的很多复杂系统，如万维网、生态网、神经网络，电力网络、城市交通网、社会关系网络等等，因此其研究引起学者们的广泛关注[1,2]。网络同步机制能解释很多自然现象，如在Internet和WWW上信息的同步交换，通信网络中的数字或模拟信号的同步交换等，所以复杂网络的同步问题是复杂网络研究的热点之一。文献[3]研究了一类具有时变时滞的复杂网络同步问题。文献[4]研究了复杂网络同步态与孤立节点解的关系。文献[5]利用牵制控制法研究了非时延和时变耦合时延的复杂网络自适应同步问题。文献[6]进一步利用间歇控制法研究非时延和耦合时延的复杂网络的同步问题。文献[7]研究了带有时延的有向复杂网络的自适应簇同步问题。文献[8]研究带有未知参数和未知拓扑结构的复杂网络的结构辨识问题。文献[9]研究了不同分数阶节点的复杂网络的投影同步问题。文献[10]研究了有向复杂网络的最优牵制控制问题。文献[11]研究了带未知参数的分数阶驱动-响应复杂网络的自适应同步问题。

目前已有的关于复杂网络同步的理论成果，主要集中在复杂网络各结点的动力学行为恒同的完全同步上，部分少数文献研究了具有常数尺度因子的投影同步问题[9]。本文研究复杂网络中的一种新的同步方式，即改进函数投影同步。由于改进函数投影同步在同步的混沌系统中引入了尺度函数矩阵，其使同步后的混沌系统的复杂程度及混沌程度增加，根据密码学原理，复杂度越大，系统越难破译，因此利用改进函数投影同步进行保密通信可进一步增加信息的安全性。考虑到网络信息安全是现代信息化社会的一个难题，而利用改进函数投影同步进行保密通信可进一步增加信息的安全性，因此在复杂网络中研究改进函数投影同步理论具有重要的理论意义和实际应用价值。文献[17]首次基于部分线性化的驱动-响应网络实现了函数投影同步。文献[18]研究具有不同混沌节点的复杂网络函数投影同步问题，文献[19]进一步研究了带有时滞的复杂网络实现函数投影同步的方法。文献[20]利用鲁棒控制法研究驱动-响应网络中的改进函数投影同步问题。文献[21]利用自适应开环加闭环控制法，研究驱动-响应网络中的改进函数投影同步问题。文献[22]研究带时变耦合时延的复杂网络的有限时间函数投影同步问题。文献[23]研究带转换拓扑结构和随机影响的复杂网络的函数投影同步问题。

本文的内容安排如下：第2节给出模型描述和改进函数投影同步的定义；第3节分别在系统模型参数已知和未知两种条件下，给出两个复杂网络实现改进函数投影同步的控制器设计方法；第4节给出两组仿真实例验证所提控制方法的有效性；第5节给出结论。

2 改进函数投影同步定义

考虑两个复杂网络模型描述如下：

取式(1)为驱动网络，带有非线性控制器的响应网络按式(2)选取。

定义1 对于驱动网络式(1)和响应网络式(2)，如果存在一个尺度函数矩阵，其中，是连续可微的函数，使式(3)成立：

本文研究的是在复杂网络模型中系统参数已知和未知两种条件下，如何设计控制器使驱动网络和响应网络达到改进函数投影同步。

3 控制器设计

3.1 两个确定复杂网络模型的改进函数投影同步法

本节研究在复杂网络模型参数已知的条件下，驱动网络式(1)和响应网络式(2)实现改进函数投影同步的控制器设计方法。

定理1 对于任意给定的尺度函数矩阵和初始条件，驱动网络式(1)和响应网络式(2)在式(4)所示控制器作用下可实现改进函数投影同步。

证明 定义每一个节点的误差向量为

将式(1)和式(2)代入式(7)有

将式(4)代入式(8)有

构造李雅普诺夫函数

将式(5)和式(9)代入式(11)有

证毕

注1 本文所设计的同步控制器是在两个复杂网络的所有状态变量全部已知的条件下获得的，若状态变量不可直接获取时，无法直接利用本文所提的控制器设计方法，此时可先构造状态观测器重构系统的状态信息，之后再利用本文所提的控制器的设计思想设计所需的控制器。

3.2 两个带有未知参数的复杂网络模型的改进函数投影同步法

本节研究复杂网络模型存在未知参数的条件下，驱动网络和响应网络实现改进函数投影同步的控制器设计方法。带有未知参数的复杂网络模型描述为

取式(15)作为驱动网络，带有非线性控制器及未知参数估计器的响应网络按式(16)选取。

定理2 对于任意给定的尺度函数矩阵和初始条件，带未知参数的驱动网络式(15)和响应网络式(16)在式(17)所示控制器和式(18)所示参数估计器的作用下可实现改进函数投影同步。

证明 把式(15)和式(16)代入式(7)有

定义系统参数误差为

把式(17)和式(21)代入式(20)有

构造李雅普诺夫函数

把式(18)，式(19)和式(22)代入式(24)有

4 数值仿真

在本节中，以由混沌Lorenz系统组成的两个复杂网络为例证实所提定理的有效性，其数学描述为

图1 Lorenz系统混沌吸引子

4.1 确定模型的同步仿真例子

本节以两个由3个节点组成的全局耦合网络为例，证实所提定理1的有效性，其中网络节点由混沌Lorenz系统式(29)组成。

驱动网络的模型被描述为

相应的响应网络的数学模型取为

图2 3节点复杂网络同步误差随时间变化图

由图2我们可以看到所有误差分量随着时间的变化而渐近趋近于零，因此驱动网络式(30)和响应网络式(32)在我们所设计的控制器的作用下达到改进函数投影同步。另外，通过大量的仿真实验，我们发现越大，复杂网络同步的速度越快，相反越小，复杂网络同步的速度越慢。因此获得结论：的取值影响复杂网络达到同步的速度。

4.2 带未知参数模型的同步仿真例子

本节以两个由10个节点组成的全局耦合网络为例证实所提定理2的有效性，其中网络节点仍由混沌Lorenz系统组成。驱动网络的数学模型为

相应的响应网络的数学模型按式(35)选取。

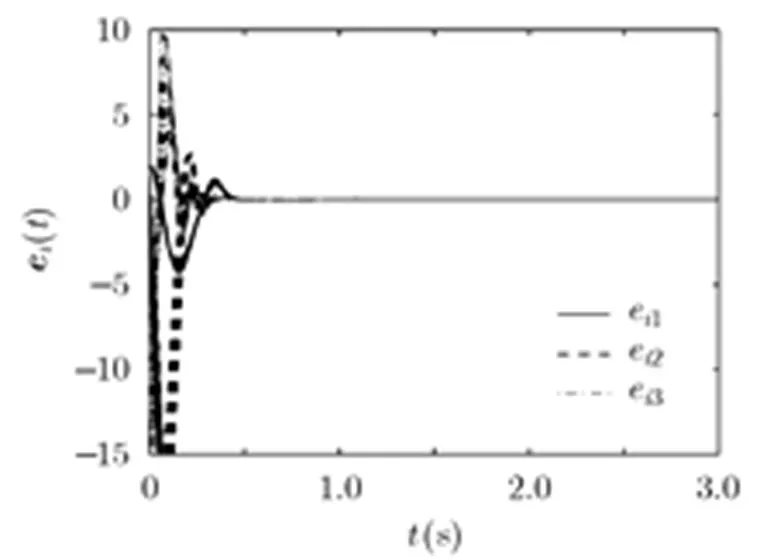
图3 10节点复杂网络同步误差随时间变化图

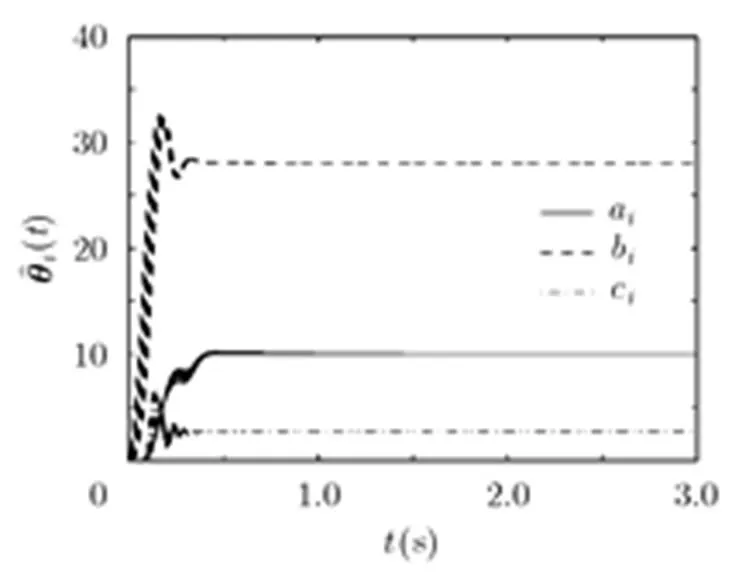
图4 10节点复杂网络参数估值随时间变化图

由以上两个仿真结果可得通过所提定理对响应网络进行控制时，响应网络的状态变量从任意初始条件出发能很快地与驱动网络达到改进函数投影同步。同时，只需修改尺度函数矩阵，便可得到其他的同步方式，如当修改所有尺度函数为1时可获得完全同步[6,7]，修改所有尺度函数为其他常数时可获得投影同步[8,9]。与研究外同步的文献[24-27]相比，本文方法不仅可以实现完全同步或投影同步，还可以实现更为一般的改进函数投影同步。

5 结束语

本文研究在两个复杂网络中实现改进函数投影同步的控制器设计方法。基于李雅普诺夫稳定性理论和自适应控制技术，给出在模型参数已知和未知两种情况下，如何设计自适应同步控制器使两个复杂网络达到改进函数投影同步。并在复杂网络模型参数未知时，给出了未知参数的估计方法。最后利用两组数值仿真例子验证了所提方法的有效性。

[1] PANDIT S A and AMRITKAR R E. Characterization and control of small-world networks[J]., 1999, 60(2A): 1119-1122. doi: 10.1103/PhysRevE.60.R1119.

[2] STROGATZ S H. Exploring complex networks[J]., 2001, 410: 268-276. doi: 10.1038/35065725.

[4] 陈娟, 陆君安, 周进. 复杂网络同步态与孤立节点解的关系[J]. 自动化学报, 2013, 39(12): 2111-2120. doi: 10.3724/SP.J.1004. 2013.02111.

CHEN Juan, LU Jun’an, and ZHOU Jin. On the relationship between the synchronous state and the solution of an isolated node in a complex network[J]., 2013, 39(12): 2111-2120. doi: 10.3724/SP.J.1004.2013.02111.

[5] LIANG Yi, WANG Xingyuan, and EUSTACE J. Adaptive synchronization in complex networks with non-delay and variable delay couplings via pining control[J]., 2014, 123: 292-298. doi: 10.1016/j.neucom. 2013.06.040.

[6] LIANG Yi and WANG Xingyuan. Synchronization in complex networks with non-delay and delay couplings via intermittent control with two switched periods[J]., 2014, 395: 434-444. doi: 10.1016/j.physa.2013. 10.002.

[7] LIU Heng, WANG Xingyuan, and TAN Guozhen. Adaptive cluster synchronization of directed complex networks with time delays[J]., 2014, 9(4): e95505. doi: 10.1371/ journal.pone.0095505.

[8] LIU Heng, WANG Xingyuan, and TAN Guozhen. Structure identification of uncertain complex networks based on anticipatory projective synchronization[J]., 2015, 10(10): e0139804. doi: 10.1371/journal.pone.0139804.

[9] WANG Mingjun, WANG Xingyuan, and NIU Yujun. Projective synchronization of a complex network with different fractional order chaos nodes[J]., 2011, 20(1): 010508.10.1088/1674-1056/20/1/010508.

[10] NIAN Fuzhong and WANG Xingyuan. Optimal pinning synchronization on directed complex network[J]., 2011, 21(4): 043131. doi: 10.1063/1.3665699.

[11] YAND Lixin and JIANG Jun. Adaptive synchronization of drive-response fractional-order complex dynamical networks with uncertain parameters[J]., 2014, 19(5): 1496-1506. doi: 10.1016/j.cnsns.2013.09.021.

[12] 孙海义, 李宁, 张庆灵. 时延复杂网络的自适应周期间歇同步控制[J]. 控制与决策, 2013, 28(5): 797-800.

SUN Haiyi, LI Ning, and ZHANG Qingling. Synchronization of delayed complex dynamical networks via adaptive periodically intermittent control[J]., 2013, 28(5): 797-800.

[13] 刘歌群, 许晓鸣. 非耗散耦合复杂网络受控同步能力分析[J]. 电子与信息学报, 2012, 34(3): 722-727. doi: 10.3724/SP.J. 1146.2011.00753.

LIU Gequn and XU Xiaoming. Controlled synchronizibility analysis for non-diffusively coupled complex networks[J].&, 2012, 34(3): 722-727. doi: 10.3724/SP.J.1146.2011.00753.

[14] 褚衍东, 李红敏, 张建刚, 等. 带有时变时滞和非线性耦合的复杂网络同步[J]. 安徽大学学报(自然科学版), 2012, 36(2): 9-14.

CHU Yandong, LI Hongmin, ZHANG Jiangang,. Synchronization of nonlinear complex network with time- varying delays[J].(), 2012, 36(2): 9-14.

[15] 张丽丽, 王银河, 王钦若. 不同维数非线性节点非线性耦合复杂动态网络渐近同步[J]. 控制与决策, 2014, 29(3): 537-540.

ZHANG Lili, WANG Yinhe and, WANG Qinruo. Asymptotic synchronization for nonlinear coupled complex dynamical networks with different-dimension nonlinear nodes[J]., 2014, 29(3): 537-540.

[16] 吴雪飞, 徐晨. 基于牵制控制的一类线性耦合复杂网络同步[J]. 深圳大学学报理工版, 2011, 28(5): 460-465.

WU Xuefei and XU Chen. The synchronization of a dynamic complex network with linear coupling[J]., 2011, 28(5): 460-465.

[17] ZHANG Rong, YANG Yongqing, XU Zhenyuan,. Function projective synchronization in drive-response dynamical network[J]., 2010, 374(30): 3025-3028. doi: 10.1016/j.physleta.2010.05.041.

[18] DU Hongyue. Function projective synchronization in drive- response dynamical networks with non-identical nodes[J].,, 2011, 44(7): 510-514. doi: 10. 1016/j.chaos.2011.04.002.

[19] DU Hongyue, SHI Peng, andNing. Function projective synchronization in complex dynamical networks with time delay via hybrid feedback control[J].:, 2013, 14(2): 1182-1190. doi: 10. 1016/j.nonrwa.2012.09.009.

[20] CHEN Ying, CAO Long, and SUN Mei. Robust modified function projective synchronization in network with unknown parameters and mismatch parameters[J]., 2010, 10(1): 17-23.

[21] DU Hongyue. Adaptive open-plus-closed-loop control method of modified function projective synchronization in complex networks[J]., 2011, 22(12): 1393-1407. doi: 10.1142/S0129183111016956.

[22] WANG Weiping, PENG Haipeng, LI Lixiang,. Finite-time function projective synchronization in complex multi-links networks with time-varying delay[J]., 2015, 41(1): 71-88. doi: 10.1007/s11063- 013-9335-4.

[23] JIN Yunguo and ZHONG Shouming. Function projective synchronization in complex networks with switching topology and stochastic effects[J]., 2015, 259(15): 730-740. doi: 10.1016/j.amc. 2015.02.080.

[24] LI Changpin, SUN Weigang, and KURTHS J. Synchronization between two coupled complex networks[J]., 2007, 76(4): 046204. doi: 10.1103/ PhysRevE.76.046204.

[25] TANG Hongwu, CHEN Liang, LU Junan,. Adaptive synchronization between two complex networks with nonidentical topological structures[J]., 2008, 387(22): 5623-5630. doi: 10.1016/j.physa.2008.05.047.

[26] WU Xiangjun and LU Hongtao. Outer synchronization of uncertain general complex delayed networks with adaptive coupling[J]., 2012, 82: 157-166. doi: 10.1016/j.neucom.2011.10.022.

[27] 毛芳芳, 蒋国平. 具有不同节点动态和拓扑结构的两个复杂网络之间的同步[J]. 南京邮电大学学报(自然科学版), 2012, 32(5): 130-134.

MAO Fangfang and JIANG Guoping. Synchronization between two complex dynamical networks with different node-dynamics and topological structure[J].(), 2012, 32(5): 130-134.

Modified Function Projective Synchronization Between Two Complex Networks with Known or Unknown Parameters

DU Hongyue LI Chunshuang GONG Libin

(,,150080,)

Recently, the complex networks have been more and more popular in various areas of science and engineering. Synchronization is one of the hot topics in the investigation of complex networks. This paper focuses on modified function projective synchronization of two complex networks with known or unknown parameters. Based on Lyapunov stability theory and the adaptive control technique, an adaptive synchronization controller is developed to realize modified function projective synchronization in two complex networks. Numerical examples are provided to show the effectiveness of the proposed method.

Complex network; Modified function projective synchronization; Adaptive control; Unknown parameter

TP273

A

1009-5896(2016)07-1816-07

10.11999/JEIT150864

2015-07-20；改回日期：2016-04-22；网络出版：2016-05-31

杜洪越 du_hong_yue@163.com

黑龙江省教育厅科学技术研究项目(12541106)

The Scientific Research Fund of Heilongjiang Provincial Education Department of China (12541106)

杜洪越： 女，1975年生，教授，研究方向为复杂网络同步、混沌同步、非线性控制等.

李春双： 女，1990年生，硕士生，研究方向为复杂网络同步.

公利滨： 男，1965年生，高级工程师，研究方向为复杂网络同步、非线性控制等.