中国地区能源强度与经济的同步收敛性研究

陈 迅，王春宝，张 勇，蒲勇健,2



中国地区能源强度与经济的同步收敛性研究

陈 迅1，王春宝1，张 勇1，蒲勇健1,2

（1.重庆大学经济与工商管理学院，重庆，400044； 2.重庆大学可持续发展研究院，重庆，400044）

各地区一直致力于缩小经济发展差距，然而作为经济发展的关键要素，能源强度及其收敛性也是至关重要的。如果地区能源强度与经济能够同时趋于收敛，那么经济发展中能源消耗总量控制的目标则是可行的。本文基于中国31个省份1997-2011年的数据，通过空间面板模型，实证分析了地区经济的收敛性以及能源强度与经济的同步收敛性。研究结果表明，中国地区经济存在条件收敛性，并且收敛速度达到每年1.98%-2.12%；伴随着地区经济收敛，能源强度也存在显著的收敛性，而且收敛轨迹呈现螺旋状；两个同步收敛过程中，地区经济收敛过程大约会提升0.02%的能源强度增长率，从而会提高能源强度的收敛水平，不过这一效应并不明显；而且，地区经济增长率和能源强度增长率均具有一定的正向外溢效应，但前者更突出。最后，基于研究结论，本文认为能源消费总量非增长目标具有现实可行性，宏观层面可以形成能源强度与能源消费总量双控机制，地方则可以因地制宜步入能源强度与经济同步收敛的路径当中。

能源强度；经济增长；收敛性；空间面板模型

0 引言

能源作为经济社会可持续发展的重要动力和关键，能源强度①的演变规律是非常重要的。它不仅能够反映经济结构转型和经济系统管理面临的能源需求，为能源政策的制定提供参考，而且还预示着经济增长过程中能源消耗总量零增长的现实可行性。从另一个角度来看，第二点的关键在于中国地区经济增长与能源强度是否具有同步收敛性。如果不同省份经济能够保持适度的收敛性增长，能源强度也能实现较快的收敛，那么能源消耗总量有可能实现非增长②。

以Solow[1]为代表的新古典增长理论认为，由于资本边际收益递减等原因，区域经济将最终呈现收敛性特征。此后，经济收敛性问题便成为学者们联系理论与实际的阵地，形成了大量的研究成果。从概念来看，经济增长的收敛性被区分为收敛、收敛和“俱乐部”收敛三大类。其中，收敛又包括绝对收敛和条件收敛两种，而且部分学者又将“俱乐部”收敛纳入条件收敛的范畴当中。尽管有关经济增长的收敛性特征并没有得到全面地证实，但条件收敛及“俱乐部收敛”现象则获得了现有研究的大量支持。例如，早期学者不仅证实拥有相似储蓄率和人口增长率的国家或地区存在收敛性，还发现其收敛速度达到每年2%左右[2] [3]，近来的研究则发现经济收敛的速度可能不止如此[4] [5]。针对中国经济增长的收敛性问题，部分学者认为自改革开放以来中国区域经济增长具有某种收敛性特征[6] [7] [8] [9]，也有学者发现这种收敛性特征很弱甚至不存在[10] [11] [12]。从研究方法来看，早期以截面回归模型或时间序列回归模型为主，近年来面板数据模型以及分布动态方法等较为流行，其中面板数据模型由于在信息使用方面的优势成为当前研究主要采取的办法。总体上，由于研究视角、研究方法和样本区间的不同，关于中国经济增长的收敛性问题并没有取得一致的结论。

如果经济增长趋于收敛，那么能源强度是否也能同时趋于收敛？近年来，这个问题引起了学者的高度重视并在多个方面取得了重要进展。在能源强度的影响因素方面，现有研究发现经济增长过程中产业结构、能源价格、技术进步等诸多因素起主要作用，但产业结构升级等因素的作用方向还未有定论[13] [14]。在能源强度收敛方面，史丹等[15]发现增长方式趋同的东部地区，其能源效率①也存在显著的收敛趋势，而中西部能源效率的差异则具有波动性特点。在能源强度与经济增长的关系方面，赵进文、范继涛[16]发现中国经济增长与能源消费的关系在改革开放前后呈现由非线性向线性转化的特征，而且经济增长对能源消费的影响具有非对称性和阶段性特征。在能源强度与经济增长的收敛性方面，Markandya et al[17]最早构建了检验能源强度差异与人均收入差异二者关系的理论模型，实证发现欧盟新老成员国之间不仅存在人均收入的收敛性特征，能源强度也同样存在收敛性特征。在同样的分析框架下，学者对中国地区经济增长与能源强度收敛性特征的研究发现，随着中国地区人均收入差异的收敛，地区能源强度差异也存在收敛[18]，而且中国与八个发达国家也存在同样的收敛性特征[19]。但是，中国区域部门间劳均GDP差异与能源强度差异的敛散性并不一致[20]。

如果能源强度能够同经济增长实现同步收敛，这就意味着，能源节约与缩小区域经济差距只是同一个发展过程的两个方面，可以通过一定的政策与措施同时加以实现。因此，针对经济增长与能源强度的时间和空间关联性，本研究将采用当前在同时考虑时间和空间因素上较具优势的空间面板计量方法，在Markandya et al[17]的基础上，构建中国区域经济增长条件收敛的空间面板模型和能源强度与经济增长同步收敛性的空间面板模型，以期推进经济增长收敛性以及能源强度与经济增长同步收敛性问题的研究，并为相关政策制定提供建议。

1 研究设计

1.1 地区经济收敛性的空间计量模型

经济增长不仅具有时间上的前后连贯性，还具有地区之间的空间关联性。不过，将时间、空间以虚拟变量的方式进入经典计量模型（1），进而对每个省份逐一进行估计，也有其不足:一是降低了模型估计的自由度；二是空间虚拟变量往往设定为东、中、西三个地区，并不能很好地反映省份之间尤其是相邻省份之间经济增长的空间关联性。相比之下，空间计量面板模型不仅同时考虑了时间和空间效应，而且不需要单独设置虚拟变量，因而更为合适。空间面板数据模型又区分为固定效应模型与随机效应模型，二者的区别在于个体效应与回归变量是否相关。本研究以特定省份作为研究对象，因而固定效应模型更为合适[24]。固定效应模型主要控制时间效应与空间效应，以此考察背景变量在控制时间、空间效应情形下对稳态水平的影响。据此，地区经济收敛性的固定效应空间计量模型可设定为：

1.2 能源强度与经济增长同步收敛性的空间计量模型

参照Markandya et al[17]的做法，将地区第期预期的能源强度与所有地区平均能源强度的差异，视为地区人均收入与所有地区平均人均收入差异的函数，弹性系数为，且伴有常数。那么，地区第期期望的能源强度与地区平均的能源强度的差异函数可定义为：

为了能够反映地区实际的能源强度的演变轨迹，有必要考虑其滞后一期的变量。参照Markandya et al，假设期实际的能源强度与前期能源强度间的差异，同期预期的能源强度与前期能源强度间的差异具有弹性系数为的函数关系，其表达式为：

（4）

综合函数关系式（3）和（4）可得到能源强度与经济增长同步收敛性的经典计量模型如下：

鉴于地区间经济增长以及能源分布同时存在的某种空间关联性，在经典计量模型（5）基础上，采用含义如前述模型相同的变量，本研究设定地区能源强度与经济增长同步收敛性的固定效应模型如下：

1.3 样本与数据

为了能够尽量全面地考察近年来中国地区经济增长的收敛性以及能源强度与经济增长的同步收敛性，本文选取1997-2011年中国31个省份（不含香港、澳门和台湾地区），总样本数为434个。其中，由于西藏缺乏历年能源消耗总量数据，因此在实证分析能源强度与经济增长的同步收敛性时予以剔除，最终样本数为420个。由于统计年鉴中宁夏缺失2001年能源消耗总量数据，本文采用前后均值予以插值补齐。其中，各地区GDP、人口总量以及能源消费总量等数据均来自《中国统计年鉴》和《中国能源统计年鉴》，并以1997年为基期对历年各地区GDP总量予以调整测算。在空间距离权重的设定方面，本文以0-1邻接矩阵作为空间距离矩阵，即空间距离矩阵中相邻地区取值为1，否则取值为0，在模型使用中则采用标准化的空间距离矩阵。其中，本文默认海南省与广东、广西省相邻。

2 实证分析

2.1 最优模型确定

在验证地区经济收敛性以及能源强度与经济增长同步收敛性方面，选择使用一般面板模型还是使用空间面板模型，需要对普通最小二乘法回归得到的残差进行空间相关性检验。如果残差具有空间依赖性，这意味着空间滞后项或空间误差项不宜忽视，空间面板模型则是较优选择。检验面板数据的空间相关性主要有五项指标，分别是：指数、以及和等统计量。其中，指数对于空间依赖性做出直接检验，后四个指标则主要为具体空间计量面板模型的选择提供依据。总体原则为：如果和统计值均不显著，则使用OLS回归模型即可；如果（或）显著而对应的（或）统计值不显著，则选择空间误差模型（或空间滞后模型）；如果和统计值均显著，此时应通过比较和的显著性做出判别，若（或）显著，那么空间误差模型（或空间滞后模型）更为合适。

鉴于此，本部分首先采用OLS以及空间相关性的检验方法，对不包括虚拟变量的地区经济收敛性模型（1）以及能源强度与经济增长同步收敛性模型（5）进行传统面板数据模型估计，以此探讨控制固定效应的必要性及空间相关的存在性。其中，估计方式依次包含混合效应面板数据模型、地区固定效应面板数据模型以及双向固定效应面板数据模型三类（见表1）。

可知，本研究中固定效应的控制是非常必要的。这是因为，不论是从表（1）列示的拟合优度还是对数似然函数值来看，地区经济收敛性模型（1）的地区固定效应与双向固定效应面板模型的统计值均高于混合效应面板模型对应的统计值，拥有更好地解释能力，而能源强度与经济增长同步收敛性模型（5）的估计结果亦是如此。综合来看，在研究地区经济收敛性以及能源强度与经济增长同步收敛性问题时，固定效应面板模型比混合面板效应模型更优。这也论证了前述根据Baltagi[24]得出的观点，即本研究选择固定效应模型更为合理。

比较混合效应模型与固定效应模型的统计检验结果根据拟合优度与似然对数值统计检验结果，可进一步对地区固定效应面板模型与双向固定效应面板模型的估计效果进行比较。对于地区经济收敛性问题，双向固定效应面板模型同时拥有比其他模型更高的拟合优度和似然对数值，因而双向固定效应模型是分析地区经济收敛性的最佳选择。对于能源强度与经济增长同步收敛性问题，双向固定效应面板模型的对数似然值略比地区固定效应面板模型高，但地区固定效应面板模型的拟合优度比双向固定效应面板模型的拟合优度高约5个百分点，因而地区固定效应模型是分析能源强度与经济增长同步收敛性的较优选择。

根据空间相关性统计检验的结果则可知，经济收敛性与能源强度同经济增长的同步收敛性均存在空间相关性，但也有所差异。首先，从混合效应面板模型的统计检验结果来看，模型（1）与模型（5）的、以及均通过了1%的显著性水平，这表明经济收敛性问题与能源强度同经济增长同步收敛性问题的研究均不能忽视空间相关性。所以，对于两个问题的研究，采用空间计量经济学的研究方法更为合适。其次，对于地区经济收敛性问题，根据双向固定效应面板模型的统计检验来看，以及和等四个统计量均显著，只是的显著性略强于，即空间滞后效应可能比空间误差效应更为突出，但两种效应均显著存在，因此在研究地区经济收敛性时，当前还不能确定应当使用双向固定效应SEM还是双向固定SAR模型。再次，对于能源强度与经济增长同步收敛性问题，根据地区固定效应面板模型的统计检验来看，只有与中只有显著，因此可以确定，地区固定效应SAR模型是分析能源强度与经济增长同步收敛性的最佳选择。

表1传统面板数据模型的估计与空间相关性检验结果

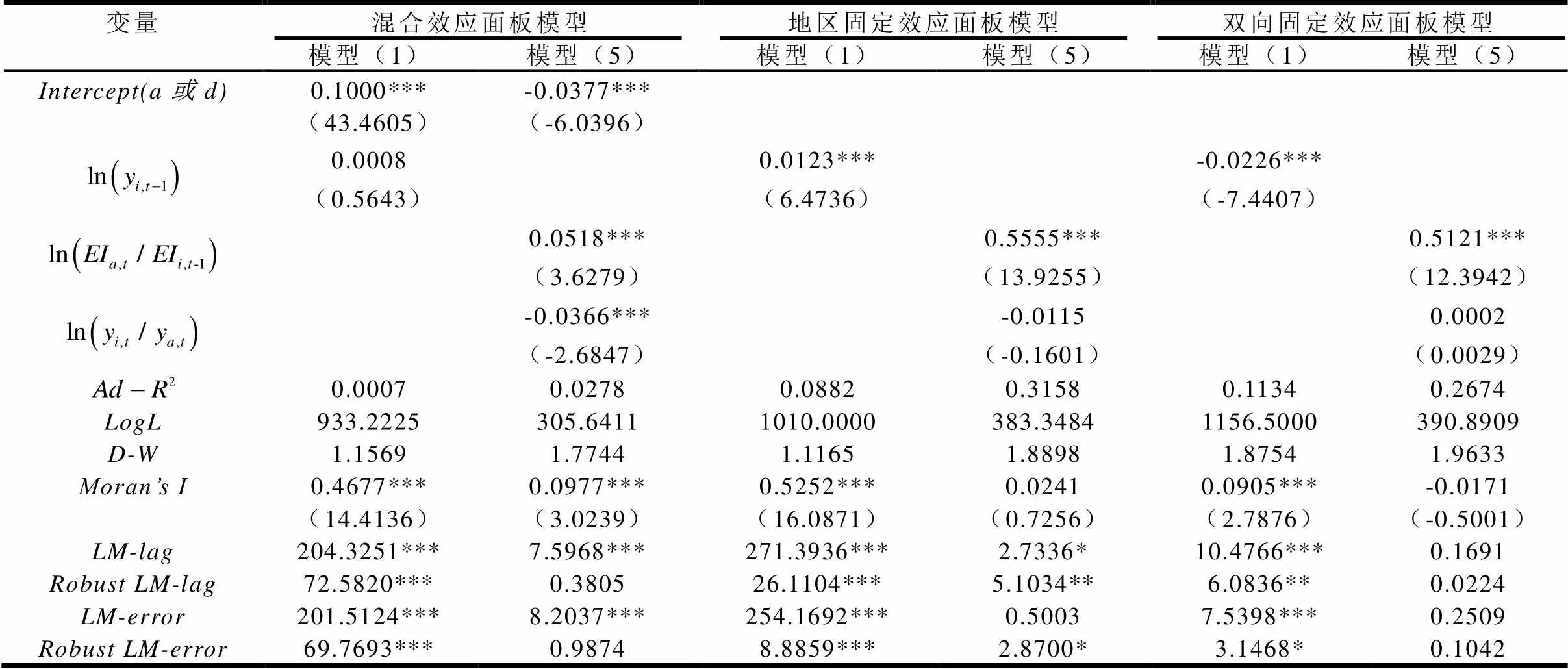
变量混合效应面板模型地区固定效应面板模型双向固定效应面板模型 模型（1）模型（5）模型（1）模型（5）模型（1）模型（5） Intercept(a或d)0.1000***（43.4605）-0.0377***（-6.0396） 0.0008（0.5643）0.0123***（6.4736）-0.0226***（-7.4407） 0.0518***（3.6279）0.5555***（13.9255）0.5121***（12.3942） -0.0366***（-2.6847）-0.0115（-0.1601）0.0002（0.0029） 0.00070.02780.08820.31580.11340.2674 LogL933.2225305.64111010.0000383.34841156.5000390.8909 D-W1.15691.77441.11651.88981.87541.9633 Moran’s I0.4677***（14.4136）0.0977***（3.0239）0.5252***（16.0871）0.0241（0.7256）0.0905***（2.7876）-0.0171（-0.5001） LM-lag204.3251***7.5968***271.3936***2.7336*10.4766***0.1691 Robust LM-lag72.5820***0.380526.1104***5.1034**6.0836**0.0224 LM-error201.5124***8.2037***254.1692***0.50037.5398***0.2509 Robust LM-error69.7693***0.98748.8859***2.8700*3.1468*0.1042

备注：表中括号内为统计值，***、**与*分别表示1%、5%和10%的显著性水平。

2.2 地区经济收敛性

前文分析得到，双向固定效应面板模型是分析地区经济收敛性问题的最佳选择，而且空间相关性不宜忽视，但还未能断定双向固定效应SEM与双向固定效应SAR模型的优劣性。鉴于此，本部分同时给出模型（6）在双向固定效应下的SEM与SAR模型估计结果并做具体分析（见表2）。

从表2显示的模型统计检验来看，双向固定效应下的空间误差模型（SEM）与空间滞后模型（SAR）的解释能力相差不大。具体表现为，双向固定效应下的SEM与SAR在模型的拟合优度上均在65%左右，经调整后均大幅下降至同一水平即11%左右，而且似然对数值也显示二者相差不大。因此，这表明在地区经济收敛性分析方面，双向固定效应下的SEM与SAR确实不存在明显的优劣之分，二者均有较好地解释能力。

表2 地区经济收敛性的双向固定效应空间面板模型回归结果

备注：表中括号内为统计值，***、**与*分别表示1%、5%和10%的显著性水平。

进一步，通过双向固定效应SEM模型估计结果可知，空间误差相关性系数显著不为零且高达0.1670，即地区间的经济增长具有显著的异质性；空间和时间固定效应系数虽然为正，但不显著，因此地区经济增长率的空间和时间效应并不明显；从地区经济上期绝对水平对本期经济增长率的影响来看，系数显著为负，这表明人均收入绝对水平较高的地区其增长率相对较低，而绝对水平较低的地区拥有更高的经济增长率，即地区之间经济增长存在条件收敛性。

根据本研究的时间间隔为一年期，结合Barro & Sala-i-Martin[2]对地区经济收敛速度的算式可知，双向固定效应SEM模型估计的收敛速度为，双向固定效应SAR模型估计的收敛速度则为。这表明，在1997-2011年的14年期间，以1997年为基期调整的人均收入衡量的地区经济正在以每年以1.98%-2.12%的速度趋于收敛。

2.3 能源强度与经济增长的同步收敛性

根据前文的分析，地区固定效应SAR模型是分析能源强度与经济增长同步收敛性的最佳选择。因此，本部分将采用地区固定效应SAR模型对模型（6）进行估计分析（结果见表3）。

从表3第2列反映的地区固定效应SAR模型统计检验来看，调整的模型拟合优度约为32%，自然对数值高达384.2548，这说明该模型具有较好地解释能力。接下来注重分析具体参数的估计结果及其反映的含义。

表3 能源强度与经济增长同步收敛性的地区固定效应SAR模型估计结果

备注：表中括号内为统计值，***、**与*分别表示1%、5%和10%的显著性水平。

当该地区在本期拥有一个低于平均的或者负的能源强度增长率（即处在图1中的第三象限），这意味着本期该地区能源强度与平均能源强度的差异将会扩大，根据系数的正定性可知，如果这个差距扩大1个百分点，下一期该地区能源强度增长率将会增加0.5491个百分点，因此很有可能在某一期该地区能源强度增长率突然变为正。随着能源强度增长率变为正，那么该地区能源强度将会转向增长，从而同平均能源强度的差距逐渐缩小，而当差距没缩小1个百分点时，该地区能源强度的增长率又会降低0.5491个百分点，即该地区能源强度的增长态势会逐渐放缓。

另一种情况则是该地区虽然上期能源强度低于平均能源强度，但在本期有一个高于平均的或者正的能源强度增长率（即处在图1中的第二象限），那么随着能源强度的本期增长，该地区能源强度与平均能源强度的差异将会缩小，如果二者的差距相比上一期缩小1个百分点，那么该地区能源强度增长率将会比上期缩小0.5491个百分点，即该地区虽然期初的能源强度低于平均能源强度，但随着能源强度的上升，差距的不断缩小使得该地区能源强度增长率将会逐渐放缓。同样地，如果某地区期初能源强度高于平均能源强度（即处在图1中的第一或第四象限），那么该地区的能源强度增长率会逐渐减小甚至变为负增长，但都存在某种调整的趋势。这种趋势，即能源强度高于平均值的地区其能源强度增长率将会逐渐减小甚至变为负增长，而能源强度低于平均值的地区其能源强度增长率则会逐渐提高。总之，每个地区的能源强度将会逐渐形成一个属于自身但类似的趋于拥有相同能源强度以及能源强度增长率的收敛轨迹。

鉴于此，本文在去掉模型（6）中不显著的经济增长收敛性变量之后，再次采用地区固定效应SAR模型进行最大似然估计，其结果如表3中第3列所示。这种处理方式不仅可以弱化不显著变量对模型估计造成的影响，而且还可以一定程度上避免能源强度收敛性与经济增长收敛行之间可能存在的内生性关系造成的估计偏误。对比表3中第2列与第3列结果可发现，包含经济增长收敛性变量与否的两种情况下，各个变量的系数、显著性以及模型统计量的估计值几乎完全一致。因此，这表明模型（6）中经济增长收敛性变量对于模型的回归估计并没有产生明显的影响。这同时也表明，能源强度收敛性的估计结果是较为稳健的，能源强度与经济增长确实存在同步收敛性现象。

图1 地区能源强度与平均能源强度差异及能源强度增长率的演变路径

当然，模型（6）主要来自类似于Markandya et al[17]所做的假设，即地区能源强度与地区平均能源强度的差异，是地区人均收入与地区平均人均收入的差异的单向函数。所以，直接在模型（6）中去掉经济增长收敛性变量的检验方法还值得商榷。因此，为了更好地避免经济增长与能源强度两个收敛过程之间的内生作用，本文参照模型（2），将能源强度的演变视为一个相对独立的系统发展过程，建立如下能源强度收敛性的空间面板模型：

模型（7）中的变量与前文变量含义一致。进一步，类似前文有关地区经济收敛性的最优模型确定方法，模型（7）的指数和LM统计量估计结果表明，地区固定效应下的空间误差模型(SEM)是最优选择①。进一步，地区固定效应下的SEM估计结果显示，为0.1668但不显著（统计值为0.1344）；为0.1370并在5%水平上显著（统计值为2.0676）；为-0.1057，对应的统计值为-5.3438，因而在1%水平上显著；为0.0634，LogL达到319.7822。类似于地区经济收敛性中的分析可知，地区能源强度增长率与初始能源强度之间呈现显著的负相关关系表明，地区间能源强度也在1998-2011年期间呈现了良好的收敛性，这在一定程度上也论证了图1所示的能源强度演变路径。因此，地区间能源强度与经济增长之间确实存在同步收敛性。

对于造成这种同步收敛性现象的客观原因，本文认为可能主要有两个方面。一方面，能源强度收敛性与经济增长收敛性之间可能存在一定的内生性关系。本文遵照Markandya et al[17]所做假设，设定了函数关系式（3），这实质上强调的是经济增长对能源强度的影响作用，与赵进文、范继涛[16]的研究结论在一定程度上是一致的，但是能源强度也可能会对经济增长具有反馈作用。尤其是，能源强度的政策目标控制和分解，可能对不同产业部门的增长速度从而整体经济增长造成影响。因此，能源强度与经济增长之间很有可能存在着某种程度的互动作用，即二者存在着内生关系。那么，这种内生性关系也可能会在能源强度收敛性与经济增长收敛行之间具有一定程度的体现。如此，模型（2）和模型（7）所反映的经济增长与能源强度两个相对独立的收敛过程，实质上则是一个互动的收敛过程。从模型（6）的估计来看，经济增长收敛性变量并没有体现出对能源强度增长率的显著影响作用，这很有可能正是因为二者之间的内生性关系所致。因此，分析能源强度与经济增长之间的相互影响，明确能源强度收敛性过程与经济增长收敛性过程之间的内生关系，值得后续研究深入探讨。另一方面，能源强度收敛性与经济增长收敛性可能共同受到诸多其他因素的影响。例如，在不考虑其他因素情况下，随着科技的发展，地区经济将会以相对较小的能耗为代价实现更快的增长，然而技术进步在区域之间具有一定的外溢性，这又会使得地区之间的技术趋同，从而推动地区间同步实现能耗下降条件下的经济增长。因此，在这些类似因素的作用下，地区间的经济增长与能源强度将逐步呈现共同的收敛性特征。从现有研究来看，有关经济增长收敛性的影响因素研究较多，但有关能源强度收敛性及其影响因素的研究则较为少见。因而，能源强度收敛性的影响因素研究，对于揭示能源强度与经济增长呈现同步收敛性的客观原因极为重要。

3 研究结论与启示

本文综合考虑经济增长自身收敛性以及经济增长与能源强度的关系基础上，构建了探讨地区经济收敛性以及能源强度与的经济增长同步收敛性的空间面板计量模型。通过对1997-2011年中国31个省份（不含港澳台地区）经济收敛性以及能源强度与经济增长同步收敛性的实证分析，本文发现地区经济和能源强度均具有收敛性，即存在同步收敛性，具体结论如下：

（1）地区经济收敛性方面，双向固定效应空间误差模型与双向固定效应空间滞后模型是最佳选择。采用这两个模型对地区经济收敛性问题的研究表明，中国地区经济增长不仅存在条件收敛性，并且收敛速度为每年1.98%-2.12%。同时，相邻地区的快速经济增长对本地区的经济增长率具有正的外溢效应，将会刺激本地区获得更快的经济增长。而且，经济增长的具有显著的空间异质性，造成模型估计误差具有强烈的空间相关性。但是，双向固定效应下的空间误差模型与空间滞后模型估计均表明，经济增长率的空间和时间固定效应并不明显。

（2）能源强度与经济增长同步收敛性方面，地区固定效应空间滞后模型是最佳选择。地区固定效应空间滞后模型的估计表明，中国地区能源强度存在着显著的收敛性，并且通过了稳健性检验。虽然每个地区的能源强度起点不同，但统一呈现一种逐渐趋于拥有相同能源强度以及能源强度增长率的螺旋状的收敛轨迹。而且，能源强度增长率呈现了显著的空间固定效应。不过，相邻地区的能源强度增长率将会给本地区带来并不明显的正向溢出效应。

（3）地区经济收敛过程可能会影响能源强度的收敛过程。从地区固定效应空间滞后模型的估计来看，地区经济收敛的过程对能源强度收敛过程中的能源强度增长率具有一定的正向作用，幅度为每年大约提升能源强度增长率0.0218%。这种影响不仅将干扰能源强度自身的收敛过程，还将提升能源强度的收敛水平，包括收敛状况下的能源强度以及能源强度增长率。但是，地区经济收敛过程与能源强度收敛过程之间是否存在双向互动的内生性关系，以及造成二者呈现同步收敛性现象的共同影响因素等，则有待后续深入研究。

基于上述研究结论，本文有着丰富的政策含义。

首先，缩小地区经济发展差距与推动各地节约能源并不矛盾，地区经济与能源强度是一个同步收敛的过程，因而能源消费总量非增长目标具有现实可行性。2012年中国能源消费总量为36.2亿吨标煤，根据目前能源消费总量预期，2015年将达到40亿吨标煤。因此，在宏观政策制定方面，可以逐渐调低预期能源消费总量的增长速度甚至在某个时间点上制定总量非增长目标，同时根据能源强度的收敛程度制定能源强度的控制目标，从而形成经济发展过程中的能源强度与能源消费总量双控机制。

其次，地区经济与能源强度虽然存在同步收敛性，但每个地区的当前状态不同，因而在趋于收敛过程中必须因地制宜加以调节。中国经济增长与能源消耗的宏观目标任务必须分配落实到每个地区，每个地区又面临自身的初始状态。因此，宏观层面和地方层面都必须要通盘考虑与因地制宜相结合，从自身当前人均收入、能源强度以及二者的增长率的实际出发，制定相应的政策配套措施，在完成当期发展目标的同时，推动经济和能源强度步入自身良性的收敛路径当中。

[1] Solow R. A Contribution to the theory of economic growth[J]. Quarterly Journal of Economics, 1956, 70(1): 65-94.

[2] Barro R J., Sala-i-Martin X. Convergence [J]. Journal of Political Economy, 1992, 100(2):223~251.

[3] Mankiw N., Romer D., Weil D. A contribution to the empirics of economics growth[J]. Quarterly Journal of Economics, 1992, 107: 407-437.

[4] Pfaffermayr M. Spatial convergence of regions revisited: a spatial maximum likelihood panel approach[J]. Journal of Regional Science, 2012, 52(5): 857-873.

[5] Próchniak M., Witkowski B. Time stability of the beta convergence among EU countries: bayesian model averaging perspective[J]. Economic Modeling, 2013, 30: 322-333.

[6] Chen J., Fleisher B M. Regional income inequality and economic growth in China[J]. Journal of Comparative Economics, 1996, 22: 141-164.

[7] 魏后凯.中国地区经济增长及其收敛性[J]. 中国工业经济,1997,(3):31-37.

[8] 刘强.中国经济增长的收敛性分析[J]. 经济研究, 2001,(6):70~77.

[9] 沈坤荣,马俊.中国经济增长的“俱乐部收敛”特征及其成因研究[J]. 经济研究, 2002,(1):33-39.

[10] 刘夏明,魏英琪,李国平.收敛还是发散？——中国区域经济发展中争论的文献综述[J]. 经济研究, 2004,(7):70-81.

[11] 王志刚.质疑中国经济增长的条件收敛性[J]. 管理世界, 2004,(3):25-30.

[12] 许召元,李善同.近年来中国地区差距的变化趋势[J]. 经济研究, 2006,(7):106-116.

[13] 史丹.我国经济增长过程中能源利用效率的改进[J]. 经济研究, 2002,(9):49-56.

[14] Hang L M., Tu M Z. The impacts of energy prices on intensity: evidence from China[J]. Energy Policy, 2007, 35: 2978-2988.

[15] 史丹,吴利学,傅晓霞,吴滨.中国能源效率地区差异及其成因研究——基于随即前沿生产函数的方差分解[J]. 管理世界, 2008,(2):35-43.

[16] 赵进文,范继涛.经济增长与能源消费内在依从关系的实证研究[J]. 经济研究, 2007,(8):31-42.

[17] Markandya A., Pedroso-Galinato S., Streimikiene D. Energy intensity in transition economics: is there convergence towards the EU average[J]. Energy Economics, 2006, 28: 121-145.

[18] 齐绍洲,罗威.中国地区经济增长与能源消费强度差异分析[J]. 经济研究, 2007,(7):74-81.

[19] 齐绍洲,云波,李锴.中国经济增长与能源消费强度差异的收敛性及机理分析[J]. 经济研究, 2009,(4):56-64.

[20] 齐绍洲,李锴.区域部门经济增长与能源强度差异收敛分析[J]. 经济研究, 2010,(2):109-122.

[21] Sala-i-Martin X. The classical approach to convergence analysis[J]. The Economic Journal, 1996, 106: 1019-1036.

[22] Baumol W J. Productivity growth, convergence and welfare: what the long-run data show[J]. American Economic Review, 1986, 78(5): 1072-1085.

[23] Abreu M., de Groot H L F., Florax R J G M. A meta-analysis of beta-convergence: the legendary 2% [J]. Journal of Economic Surveys, 2005, 19(3): 389-420.

[24] Balatagi B H. Econometric analysis of panel data(second edition) [M].John Wily & Sons Chichester, United Kingdom,2001.

The Simultaneous Convergence of Energy Intensity and Economy in China

CHEN Xun1, WANG Chun-bao1, ZHANG Yong1, PU Yong-jian1,2

(1. School of Economics and Business Administration, Chongqing University, Chongqing 400044, China;2. Institute for Sustainable Development, Chongqing University, Chongqing 400044, China)

Regions in China have always been committed to reducing the economic development gap. However, energy intensity and its convergence are also key elements of economic development. The region's energy intensity (EI) and economy tend to converge simultaneously. Energy conservation and reduction of regional economic disparities are two aspects of the same development process, which means that non-growth target of total energy consumption in the economic development is feasible.Based on Markandya et al.’s (2006) study, our research constructed two spatial panel econometric models for inspecting conditional convergence of regional economy and simultaneous convergence between regional EI and economic growth. The study collected data from 31 provinces of China in from years 1997 to 2011. Overall, this paper is mainly organized into four parts. The first part is introduction and literature review. The second is model construction. The third is an empirical analysis of economic convergence and simultaneous convergence of EI and economy. The main conclusions are summarized in the last part as follows: I. Regional economic growth in China shows conditional beta convergence at a rate of 1.98% to 2.12 % per annum. Meanwhile, the rapid economic growth in adjacent areas has a significant positive spillover effect on certain areas, which will stimulate the region for faster economic growth.II. There is also a significant convergence characteristic for regional EI in China. Regional EI presents one kind of spiral convergence trajectory for the same EI level and growth rate. However, for a certain area the positive spillover effect of EI growth in adjacent areas is not obvious.III. The convergence process of regional economy has a weak and positive effect on increasing at about 0.02% rate per year for EI and EI convergence. This effect will not only influence the process of EI convergence, but also the convergence level of EI.Based on the above conclusions, we propose two policy implications. First, we can gradually reduce the target of total energy consumption even for a non-growth target on the macro level. A dual control mechanism for regional EI and total energy consumption can also be developed. Second, local conditions in regions must be seriously considered for simultaneous convergence of EI and economy.

energy intensity; economic growth; convergence; spatial panel model

中文编辑：杜 健；英文编辑：Charlie C. Chen

F206

A

1004-6062(2016)03-0216-08

10.13587/j.cnki.jieem.2016.03.027

2013-10-14

2014-03-08

国家社会科学基金重大资助项目(12&ZD209)；中央高校基本科研业务费资助项目(CDJXS12021106)；重庆市“两江学者”计划专项经费特聘教授资助项目

陈迅（1950—），男，河南巩义人，重庆大学经济与工商管理学院教授，硕士，研究方向：数量经济、产业经济与区域经济。

①能源强度（Energy Intensity，EI）采用同年地区能源消耗总量除以地区GDP得到，即单位产出的能源消耗量（万吨标准煤/亿元）。

②一个简单的例子予以说明。假设仅有2个地区A和B。第0期，GDPA为1.6单位，EIA为2，GDPB为2单位，EIB为1，那么第0期A与B的能源消耗分别为3.2单位和2单位，合计5.2单位。第1期，A地区和B地区经济分别实现增长率gA为10%，gB为7%，能源强度EIA和EIB分别演变为1.65和1.07，可得到第1期A与B的能源消耗分别为2.904单位和2.2898单位，合计5.1938单位。第2期，A和B地区经济增长率gA和gB分别演变为9%和8%，能源强度EIA和EIB分别演变为1.35和1.12，可得到第2期A与B的能源消耗分别为2.58984和2.588544单位，合计5.178384单位。持续下去，经济增长和能源强度实现同步演变（收敛），A和B地区经济发展过程中能源消耗的总量不仅没有实现增长，反而逐年减少。

① 原文所指的“能源效率”即“地区产出—能源效率”（地区GDP与能源消耗总量的比值）。因此，实质上原文的“能源效率”与本文的“能源强度”内涵一致，只是二者互为倒数关系，此处沿用原文名称。

① 限于篇幅，本处未详列模型（7）的传统面板数据模型估计结果与空间相关性检验结果，有兴趣的读者可向作者索取。