多车型多车槽VRP的混合导引反应式禁忌搜索算法

王 茜，吉清凯, ，胡祥培



多车型多车槽VRP的混合导引反应式禁忌搜索算法

王 茜1，吉清凯1, 2，胡祥培2

（1.中山大学管理学院，广东广州，510275；2.大连理工大学系统工程研究所，辽宁大连，116023）

多车槽多车型VRP问题在燃油、食品等行业的应用变得越来越普遍。本文充分考虑多车槽多车型双重属性，在构建HFFMCVRP的三下标流数学模型基础上，将反应机制与导引机制有机结合，提出一种混合的导引反应式禁忌搜索算法予以求解。该算法不仅利用反应机制有效增加禁忌搜索的灵活性，而且改进的导引机制可修正寻优过程中潜在的“误导”性。实验结果表明，该算法可通过反应机制与导引机制动态调整算法深度搜索与多样搜索的平衡，从而有效地求解HFFMCVRP问题。

多车槽；多车型；导引机制；反应机制；禁忌搜索

0 引言

车辆路径问题(Vehicle Routing Problems，VRP)[1]是实现物流配送系统高效、低成本运作的难点和热点问题，自1959年由Dantzig和Ramser提出后备受学术界关注。随着VRP自身理论与现代物流业的高速发展，实际应用中的VRP呈现出复杂形态，即所谓的“复杂VRP(rich VRP)”，从而衍生出诸多侧重研究不同因素的VRP模型。

在物流配送中，为满足排斥性货物低成本准时送达到客户，多车槽车辆路径问题(Multi-Compartment Vehicle Routing Problems, MCVRP)的应用较为常见，如牲畜饲料配送中，对病毒极其敏感的兔子饲料不能使用曾经装载过牛科动物饲料的车槽装载，以免发生感染；同样，为满足各类生鲜冷热、易腐、易溶食品对不同温度、湿度的需求，便利店的食品配送中也需要提供不同环境的独立车槽(或某种可移动、封闭的容器)；此外，还有可回收垃圾运输以及不同燃油配送等。多车槽车辆除能满足不同情况下货物“隔离”的要求外，在节约配送成本上相对于独立运输也有较为明显的优势[2-3]。而物流配送企业往往会在不同时期购买不同的车型以满足自身发展、灵活响应不同的运输需求，从而形成了配送车队车型的异质属性，即车队中有多种型号的车辆。因此，现实的物流配送中，尤其对于燃油类、食品类、环卫部门等企业，多车型与多车槽两种属性共存的车辆路径问题，即多车型多车槽的车辆路径问题(Heterogeneous Fixed Fleet Multi- Compartment Vehicle Routing Problem, HFFMCVRP)越来越普遍。

而目前的VRP研究中，往往侧重于多车槽[2-4]或多车队[5-17]某一方面的研究，较少综合考虑二者在实际物流运输中关联性的研究，相关企业难以找到运营决策的理论依据。本文综合考虑多车型与多车槽双属性的VRP问题，提出了求解HFFMCVRP问题的混合的禁忌搜索算法。本文研究成果在一定程度上扩展了VRP的研究，具有一定的理论价值；也为燃油、食品运输等实际HFFMCVRP应用企业提供了运营决策支持，提高物流企业运营效率，改善顾客服务质量具有广泛的现实意义。

1文献综述

近年来，学者们对经典VRP 进行了大量卓有成效的研究工作。本文主要对“多车槽”与“多车型”国内外学者的研究进展进行了梳理与归纳。

1.1多车槽车辆路径问题及其算法综述

尽管早在80年代就有研究者对燃油配送中的“多车槽”运输进行了研究，但直至2008年多车槽车辆路径问题(MCVRP)才由El-Fallahi等[3]正式提出。在MCVRP研究中，客户可以有多种货物需求，而车辆有多个负责装载不同货物的车槽。车辆的装货车柜由隔离壁(Separator)分隔为多个车槽。针对车槽数的VRPC问题，Fallahi等采用等分和随机分割两种方式，将CVRP经典算例中的客户需求一分为二，而获得所需算例，并将MCVRP按货物种类数分解为个经典VRP问题,通过C-W节约法求解得个VRP初始解，从而获得MCVRP的初始解；同时并用迷因算法(Memetic Algorithm，MA)与禁忌搜索（Tabu Search, TS）两种算法分别对其进行优化；最后，通过比较同一客户的可分开运输与必须同时运输两种订单的运输成本，结果发现前者比后者成本更小。尽管El-Fallahi等提出的“分解、组装”策略较好地解决了MCVRP的“多车槽”约束，但其过程略显费解与耗时。Muyldermans等[2]于2010年根据MCVRP的“多需求多车槽”特性，引入一个客户及订单的组合结点方法，改进了El-Fallahi提出的“分解、组装”的步骤，直接应用经典VRP的改进算法，将邻域表标记(Neighbor Lists and Marking)以及导引式局部搜索算法(Guided Local Search)结合，前者用于提高搜索速度，后者用于提高搜索质量；求解相同算例的结果表明，其GLS比El-Fallahi等的MA与TS更快，解的质量也有1%-2%的提高；这一研究成果成功被应用于城市垃圾回收过程的“共同回收 (co-collection) ”，有效节约回收成本。此外，Muyldermans等学者的研究还发现，在货物种类更多、车载量增加、更多客户有多种货物需求等情况下“共同回收”带来的成本节约更显著。2010年，Derigs等[4]基于前人的研究，提出较完善的、可方便扩展的MCVRP数学模型。该模型首次考虑车槽与货物的排斥性与车槽结构，将订单而非客户作为MCVRP中的最小操作单元，将多种算法模块，如大邻域搜索(Large Neighborhood Search)、局部搜索与亚启发式算法——包括基于属性的爬山算法(Attribute Based Hill Climber)、大洪水法(Great Deluge Algorithm) 、纪录更新算法（Record-to-Record Travel algorithm）、模拟退火算法(Simulated Anealing)——进行组合实验，寻求最佳的算法模块组合。与El-Fallahi等、Muyldermans等的算法相比，Derigs等的算法求得的结果平均约有1%的提高。

上述文献中使用的MCVRP算例有部分是通过对VRP算例进行需求二等分获得的，即VRP算例的解空间包含了相应MCVRP算例的解空间。但是，由于多车槽的约束，上述针对MCVRP提出的算法在求解相应的VRP算例时，均无法全部求得VRP的已知最优解（Best Known Solution, BKS），而求解MCVRP的结果相对于VRP的BKS则有更大的偏差，这也表明了MCVRP的求解质量仍有提高的空间。目前国内学者暂无有关MCVRP方面的研究。

1.2多车型车辆路径问题及其算法综述

在实际的物流配送中，配送中心车队可能由多种运输成本和装载量不同的车型组成，称为混合车队车辆路径问题(Mixed Fleet VRP, MFVRP)或多车型车辆路径问题(Heterogeneous Fleet VRP，HVRP)[5]。HVRP一般根据车队规模分为规模固定的多车型车辆路径问题 (Heterogeneous Fixed Fleet Vehicle Routing Problem, HFFVRP) 与车队规模与组合车辆路径问题(Fleet Size and Mix Vehicle Routing Problem, FSMVRP)两类。Taillard[6]于1999年首次研究HFFVRP问题。HFFVRP中车队的异构表现为装载量、固定成本与可变成本、速度、最大旅行时间与可用性等多方面，而目前的研究主要是装载量与成本方面的异构。在实际应用中，FSMVRP适用于战略决策支持，即配送中心购买何种组成结构的车队最实惠；而HFFVRP适用于战术层和操作层的决策支持，即如何高效地调用已有规模固定多车型车队。Taillard对HFFVRP的“拆分、组合”的处理思路与Fallahi等对VRPC的处理思路相似，而二者都是对新问题的首次研究。然而，这种处理方式因为比较复杂，所以在后续研究中研究者都较少使用。

Tarantilis是研究HFFVRP较深入的学者之一。其最初应用可回溯式门槛接受法(Backtracking Adaptive Threshold Accepting algorithm, BATA)[7,8]求解HFFVRP。与传统门槛接受算法不同，在BATA算法中，门槛值不单可以逐渐下降，当门槛接受条件一次都不满足时它还可以上升，或称回溯。在回溯过程中，上升值必须比回溯执行前的那一个门槛值小。相对传统门槛接受算法，BATA更灵活而且更有效地向全局最优收敛，在解的质量上平均提高了0.31%。基于列表的门槛接受法(List Based Threshold Accepting algorithm, LBTA)是Tarantilis等[9]提出的求解HFFVRP的第二种算法，是对传统门槛接受算法的另一种改进。LBTA在局部搜索的过程中，利用解的信息不断更新门槛值列表，并依此列表更新门槛值。在使用相同的邻域结构的情况下，BATA比LBTA求解效果更优，前者能够求得T-8算例6个较优解。在实际物流配送中，Tarantilis等[10]提出一种混合算法用以求解鲜奶配送与预混混凝土运输中的HFFVRP问题。该算法使用禁忌搜索改进，由GEROCA (Generalized Route Construction Algorithm)构造初始解，并利用AMP组合优秀解特性形成不完全解，再用GEROCA补充得完整解。该算法对实际案例的求解优于LBTA和BATA。但关于T-8算例，该文献中并没有相关求解结果。Tarantilis等[11]人提出导引式禁忌搜索(Guided TS, GTS)是目前求得T-8算例最优解的算法之一。GTS的初始解构造方法与LBTA、BATA相同，Tarantilis等先将其模拟成装箱问题，即逐个计算尚未被服务客户的需求与各车辆空余装载量的差值，并将最小差值所对应的客户分派给相应的车辆，直到所有客户都被服务。这种初始解构造法能构造出T-8算例的初始可行解。此外，除了经典的2-opt外，GTS还应用了新颖的邻域结构——对每一对路径，交换两条路径中的客户结点序列(Bone，从长度可从0至整条路径)。通过为候选解中的每条边定义一个客户结点到各连接结点的距离平均值改进效用函数，重新定义“不被期望的长边”并通过惩罚这些边以摒弃非期望解的特性，对TS进行引导。

2007年，Li等[12]提出的纪录更新算法(其简称HRTR)，亦是目前求解T-8算例效果最佳的算法之一。HRTR将Relocate、Swap、2-opt与Or-opt四种邻域结构分别以纪录更新(record-to-record travel)与下坡(downhill)两种方式执行，并针对HFFVRP复杂的解空间，在传统纪录更新算法基础上增加全局纪录与全局偏差量，用以接受扰动解，增强算法跳出局部最优解的性能，并能求出T-8算例的7个所知最优解。Li等[13]于2010年应用一种混合路径重连(path re-linking，PR)算法的“多重启动”的适应性记忆规划法(multi-start adaptive memory programming, MAMP)来求解HFFVRP。其中，MAMP每一次迭代构造多个有潜力的初始解，进而由禁忌搜索进行改进；PR算法则作为强化搜索的策略融入MAMP中，以增强其构造优质解的能力。在求解T-8算例的表现上，该算法求得的可变成本比GTS、HRTR稍差，只求得5个可变成本的所知最优解，但在总成本方面较GTS、HRTR稍强(平均约0.3%的成本降低)。

HFFVRP除了有重要的理论研究意义外，还有广泛的实际应用价值，其研究成果往往作为核心模块被嵌入DSS中，以支持企业配送中心的运营管理。如Prindezis等[14]于2005年为雅典中心食物市场公司开发了一个基于网页浏览器的物流管理系统，其核心是禁忌搜索求解HFFVRP；Tütüncü[15]于2010年提出基于一种新的贪婪式随机自适应记忆规划搜索算法(Greedy Randomized Adaptive Memory Programming Search)的可视化交互方法，并将其嵌在ADVISER的决策支持系统的应用中。

国内最早由郭耀煌等[16]于1992年对HFVRP进行研究，并同时考虑了多车场的属性，其工作主要是围绕如何将HFVRP按“优先分配装载量大的车辆”原则并用里程控制方法将HFVRP化简为多个单一车型VRP，然后分别进行求解。2001年，李嘉等人[17]针对城市货运出租公司车辆分派管理、搬家公司搬运车辆分派管理等领域展开研究。研究中车辆有统一的最大允许工作时间限制，各个客户也有时间窗等要求。且每个客户单次可能需要不只一辆车为其服务且对车型有所限制。针对此特殊问题，他们提出了两阶段方法，即第一阶段采用枚举的办法用启发式每次生成一个车队模式；第二阶段在“车队+客户”的组合染色体编码结构下，用一种混合算法(TS对GA产生的后代进行预改进)求解。同时，袁庆达等[18]研究了带软时间窗的HFFVRP(HFFVRP with Soft Time Windows)。其先用GENIUS(GENeralized Insertion & Unstring and String)算法按加入时间坐标的三维距离来构造初始路径，然后为每条初始路径构造一个辅助图，在中确定每段边使用何种车型服务能获得的最小服务成本和求解的最短路，确定所对应初始路径的最优车辆组合，用TS算法进行优化，使用按均匀独立分布生成的算例对算法进行验证。2008年，李建等人[19]研究第三方物流中的带硬时间窗的HFFVRP(HFFVRP with Hard Time Windows，HFFVRPHTW)。鉴于第三方物流的复杂性与“优先分配装载量大的车型”的原则，其在研究中没有考虑到车辆的运输可变成本，而优先满足最小费用车型策略来分配车辆，再用融合SA的混合GA来对车辆的再分配和路径优化，最后使用随机生成的算例验证其算法与车辆分配策略的合理性。

由于国内最先提出HFVRP时是伴随着多车场属性提出，因此国内学者对多车场HFFVRP(Multi-Depot HFFVRP，MDHFFVRP)关注颇多。在MDHFFVRP研究中，对于“多车场”的处理，普遍采用启发式算法与一定分配原则相结合，将多车场问题转化为单车场问题的策略。如郑丽英[20]等于2009年使用隶属度变异全局搜索聚类算法，针对染色体结构中客户排程与车辆安排两部分设计了5类交叉算子，并用GA求解。钟石泉等人认为，尽管简单的“化多为一”的作法可行，但却都没有从整体上来考虑多个车场，而且其使用的划分规则在约束比较多的情况下对车辆调度的全局优化有很大影响。因此，他提出了多车场同时优化的方法，而以随机分派的方式对多车型约束进行处理，并使用带局部禁忌表与全局禁忌表的改进TS优化求解。2009年，王晓博等[21]人针对多车场、多车型装卸一体化车辆路径问题(MDHFFVRP with Backhauls，MDHFFVRPB)研究。他们也认为由于MDHFFVRPB的特殊性，简单地“化多为一”容易导致配送和集货这两个因素权衡分析不充分，造成车辆资源的浪费、增加运输成本，并容易陷入局部最优解。因此他们提出符号和自然数混合的编码形式从整体上考虑MDHFFVRPB，并提出一种利用TS对GA的精英种群改进搜索的混合算法。实验结果表明其混合算法优于前人的多阶段启发式算法，并得出“多车场多车型”比“多车场单车型”运营策略更有效的结论。与本文研究内容较相近的是国内学者戴锡等[22]对油品配送的研究。其研究问题具有多车场、多仓库、多商品、多舱位（即车槽）、多车型、时间窗等诸多特性与约束，为应对其复杂性并提高应用开发的适用性，其以两阶段启发式算法为基础，给出了人机交互式的求解方法。戴锡等的研究深入说明了本文的现实意义，本文亦为相关的现实应用开发提供了理论基础。

2 数学定义与模型

HFFMCVRP问题的求解目标是在满足以下约束的情况下找到最小总成本的车辆分配与行车路线，其数学模型如下：

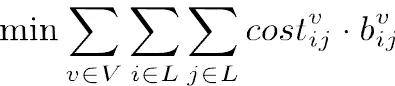
s.t.

(2)

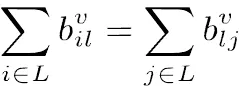
,,(4)

(5)

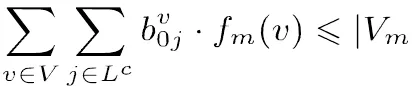
,(7)

(8)

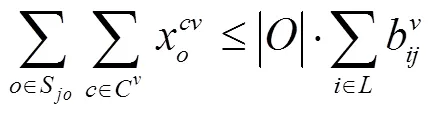
,,(10)

,,(11),,(12),,(13),(14),,(15)

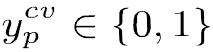
式(1)为模型的目标函数，表示所使用车的可变成本之和最小。表示车辆从客户直接到达客户，否则为0。式(2)表示每辆车最多只从配送中心出发一次。式(3)表示车进入结点，必然也从离开。式(2)和式(3)表明若车被分派任务，则必须从配送中心出发并最终回到配送中心。式(4)表示若车从驶到，则的“位置”比的“位置”高，即在车行驶路径中的位置。式(5) 将配送中心设在所有路径首端，以消除结点次序不同但实质相同的重复路径。式(4) 和式(5)用于共同消除子路径。式(6) 表示各种车型使用的车辆数不超过限制。是车辆关于车型的特征函数，若车辆，则，否则为0。（7）式表示车辆车槽装载货物量不能超过其限载量。表明订单由车的车槽运输，否则为0。式(8)表示每个订单只由某一辆车的某一个车槽为其服务。式(9)表示，若客户的某些或全部订单由车辆服务，则车辆必定访问客户。式(10)表示若某些或全部所订货物为的订单，由车辆的车槽负责运输，则货物由车辆的车槽负责运输，即。式(11)和式(12)描述货物不兼容的约束条件，式(13)~式(16)则定义模型的决策变量。

上述模型较完整地对HFFMCVRP进行了描述，但在实际物流运输中，存在不同的应用，从而模型的目标函数与约束条件均会发生细微变化。比如，在实际物流运输中，经常出现运力不足的情况。此时，需要决定哪些订单需求应优先处理，哪些订单暂时不处理。为此，可引入新的决策变量，表示订单暂时不处理，表示订单优先处理。若订单未被服务，则产生一个惩罚成本，与订单的需求量相关，或者可根据实际情况另外定义。此时，目标函数将发生变化，式(1)变为

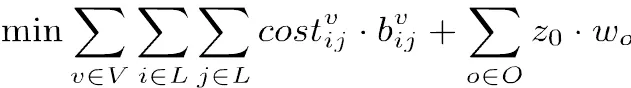
又如，在实际物流运输中，对需求、装载量的衡量可能有多个维度，比如不仅考虑重量还考虑体积约束。此时，无需添加新的决策变量，而只需增加类似式(7)的约束条件即可。此外，上述模型中不允许对一个订单进行切割，即每个订单只由一辆车一次性完成服务。但在实际物流运输中，存在将订单进行切割并分别在多个车槽或多辆车中完成运输的情况，则需定义一个订单的切割方式，即是任意切割为多个小订单还是按某种规则进行切割。此类扩展需定义更多的决策变量与约束条件。

3 算法设计

3.1初始解构造及邻域搜索

对于HFFMCVRP问题需要同时考虑多车型与多车槽的双重属性，与多车槽属性对应的是客户的多订单属性，客户的不同订单对应不同的货物。某客户的一个订单只能由一辆车一次完成服务，但一个客户的不同订单可以由同一辆车也可由不同的车服务。因此，HFFMCVRP中的最小服务单元应是订单结点而不应是客户结点。本文在Tarantilils等人[11]提出初始解构造法基础上，结合HFFMCVRP双属性特征，将HFFMCVRP模拟成一个装箱问题，为每一客户定义一个表示所有从某结点出发边的平均长度；然后对每一订单与符合装载约束车槽间计算“匹配度”，每次将最大“匹配度”对应的订单分派给相应的车槽，重复此操作，直至所有订单均被服务。在初始解的构造过程中，不仅考虑了车槽装载量与订单需求量间的匹配，而且能顾及到已服务订单与没有服务订单间的“匹配”。该改进的初始解构造法能快速构建HFFMCVRP的初始可行解。HFFMCVRP中的车队为异质且规模固定，现考虑一支由3辆A型、2辆B型的车辆组成的车队。首先，对应每一辆车，生成一条空路径，即生成“A, A, A, B, B”五条带有A型车、B型车特征的路径。然后按程序1生成可行初始解。具体如下：

程序1 初始解构造

(1)根据需求量大小将订单按升序排列；

(3)在保持可行性的条件下，使用最小成本插入法依次将未服务订单逐个插入中；

(4)更新各车槽剩余装载量，重复步骤(2)与(3)，直到所有的订单被服务。

确定初始解之后，需搜索解的邻域以寻求更优解。本文采用了2-1 move, 1-1 move, 1-0 move, 和 2-opt*以及swap, relocate 和 2-opt等经典的邻域结构。由于VPR问题的复杂性，即使是亚启发式算法在求解中-大规模问题时，寻求邻域最优解也需要巨大的计算量,耗时较长。学者们利用“邻域范围缩减策略”，过滤掉一些被认为潜在价值相对较小的邻域解，将计算集中在某些合意的邻域以减少计算量。本文在邻域搜索中允许一个非禁忌的操作当且仅当该操作连接的边满足订单对应的客户是订单对应的客户的邻居的条件，即

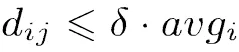
3.2导引反应式禁忌搜索算法

导引机制是一种依据设定效用函数识别并惩罚不良属性边，以导引搜索进入未开拓解空间搜索方法，其效用函数及惩罚参数设计不同，会存在误选或惩罚“过度”或“过轻”的问题。本文在Tarantilis[11]提出的引导机制的基础上，引入矩阵记录边在优良解中出现的频率，利用搜索过程的历史信息修正引导机制寻优过程中潜在的盲目性；同时将动态控制禁忌周期的反应机制与导引机制相结合，提出一种混合的导引反应式禁忌搜索算法。该算法利用反应机制直接调整邻域范围参数以有效引导禁忌搜索的方向；若TS连续表现良好，则调整该参数缩小邻域范围以深化搜索；反之调整该参数扩大邻域范围以放宽搜索，从而动态调整算法深度搜索与多样搜索的平衡，增强了算法的寻优能力。

在调度问题或VRP的求解中，长距离的边往往被认为具有不良属性并进行惩罚，从而在未来搜索中该边极有可能被避开。Tarantilis等人[11]对传统导引机制做了延伸，成功应用于HFFVRP问题。其效用函数为，不仅考虑了边的距离和惩罚次数，还考虑了结点和相对其它结点的平均距离，从而使边的选取更加科学。传统导引机制中，虽然效用函数使用、和等参数使边的选取更准确，但由于和两个参数是问题本身固有属性，也只是关于导引机制中惩罚操作的信息，其并未包含关于搜索过程的历史信息。而对历史信息的有效利用能够提高未来搜索的性能[23]。为有效利用历史信息，本文引入一个矩阵来记录边在优良解中出现的频率，根据搜索的历史信息来进行边的选取的效用函数。每个元素初始值为1，每次搜索到最优邻域解时，对中的每条边更新其对应的，即当时，，否则令, 其中是当前所发现的历史最优解。在程序3的步骤2中，当搜索被认为陷入循环时，被设置为其缺省状态，即全部元素为1的矩阵。这样做可进一步给予算法一定的自我改正功能。这一步骤亦是连接导引机制与反应机制的重要一步。

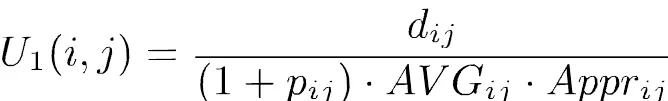
(19)

(20)

式(18), (19), 和 (20)定义了三个效用函数，无论在哪个效用函数中，若边多次出现在优良解中，其值就越高，从而越低，被选中进行惩罚的可能性就越低。

程序 2 导引机制

else

而反应式的禁忌搜索(Reactive TS，RTS)是Battiti与Tecchiolli[24]受动力系统理论启发后提出的一种禁忌搜索算法。本文根据搜索过程调整禁忌表长度以将搜索轨迹放宽，从而不受限于搜索空间的局部区域，其鲁棒性及参数变动对其性能的微弱影响已得到证明[25-28]。在本文中，反应机制除了动态调整禁忌表长度外，还调整邻域范围；当搜索陷入局部最优时，还通过开/关邻域范围缩减策略和缺省化导引机制中的矩阵来使搜索跳出局部最优。(见程序3中的步骤(2))。RTS流程及其参数描述如下：

参数 含义

程序3反应机制

else

当求解过程陷入混乱时，Battiti等人提出的反应机制中，逃脱程序实质上是一系列的随机搜索。而本文使用另一个较长含有历史最优解目标值的“禁忌表”来检测重复，即当在中时，则目标值的重复被检测。除了禁忌表长度动态调整外，本文用这个开关来开启/关闭邻域范围缩减策略。当搜索被认为是陷入混乱时，关闭邻域范围缩减策略，从而使搜索范围扩大以帮助搜索“逃脱”；若下次迭代未检测到重复，则重新开启邻域范围缩减策略，从而动态调整搜索深度与广度。现在给出算法 RGTS的整体框架：

启动程序1 获取初始解。

: 依次使用路线间操作,,改进当前解，再依次使用路线内操作,和改进当前解。每个操作后都更新当前解。最终返回一个未禁忌的邻域最优解。

启动程序 2。

启动程序 3。

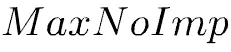
4 实验设计与分析

4.1 HFFMCVRP算例集

由于现有研究中尚无HFFVRPC的国际标准算例，本文根据Taillard[6]的HFFVRP标准算例，采用如文献[2][3]的算例生成方法，将HFFVRP的国际标准算例T-8做“二等切分”变换，即将车辆装载量与各个客户需求二等分，使每辆车有二个装载量相等的车槽，每个客户有两种数量相等的需求，而第个车槽只能装载第种需求，如此生成算例TC-8，详见表1。

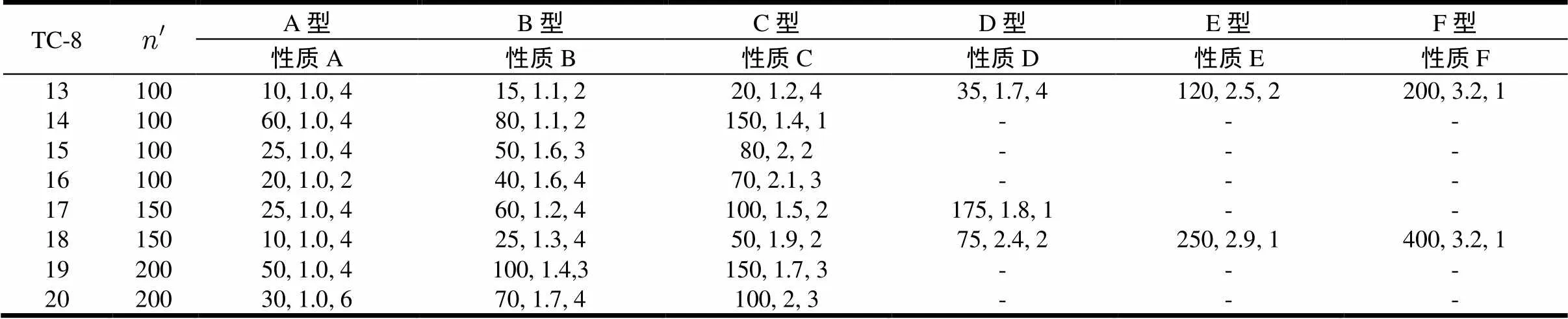
表 1 TC-8算例属性

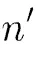
TC-8算例的复杂性不仅在于多车槽、多订单的约束，而且在结点规模上亦是T-8算例的两倍。将有个客户结点、条边的HFFVRP算例二等分后，生成一个有个订单结点、条边的HFFMCVRP 算例，如的情形如图1所示，其中正方形表示客户结点，圆形表示配送中心，三角形表示客户结点的订单。这意味着HFFMCVRP将会拥有更大的搜索空间与更多的局部最优解。同时，由于T-8算例将同一客户的两个需求同时派送，所以T-8的可行解也可认为是TC-8的可行解。TC-8算例解空间是将T-8算例解空间的多重细分，T-8算例中的每一个可行解在TC-8中可能以多种形态出现。

图1 HFFVRP算例与HFFVRPC算例的关系

4.2 实验结果与分析

算法RGTS在Windows XP系统下、Visual Studio 2008 C#编程环境中实现，并在配有主频为1.32GHz的Intel 奔腾双核T4300 处理器与1GB DDRII内存的笔记本电脑上运行。

4.2. 1参数设置

表 2 RGTS的参数设置

与许多亚启发式算法相似，RGTS需要对其参数进行调试以求计算量与求解质量间的平衡。由于反应机制多次成功应用于[25-28]文献中，因此本文反应机制参数设置基本参考上述文献参数设置。为避免早期迭代时过度频繁的禁忌表长度调整，本文经过测试将的初始值设为而不是 标准RTS中的“1”。关于导引机制的参数设置，本文生成5个随机算例，变动各个导引机制的参数，在中变动，在中变动，并记录其对应的求解质量，最后得到较优的参数组合。对于其它参数和亦在多次试验后确定参数值，具体如表2所示。

4.2. 2有无导引机制的TS求解TC-8算例的比较分析

为进一步了解导引机制的作用与效能（扩大算法的搜索广度），图2展示了标准TS（图中灰色）与有导引机制的TS（图中黑色）在求解TC-8中的问题19时的搜索迭代曲线。

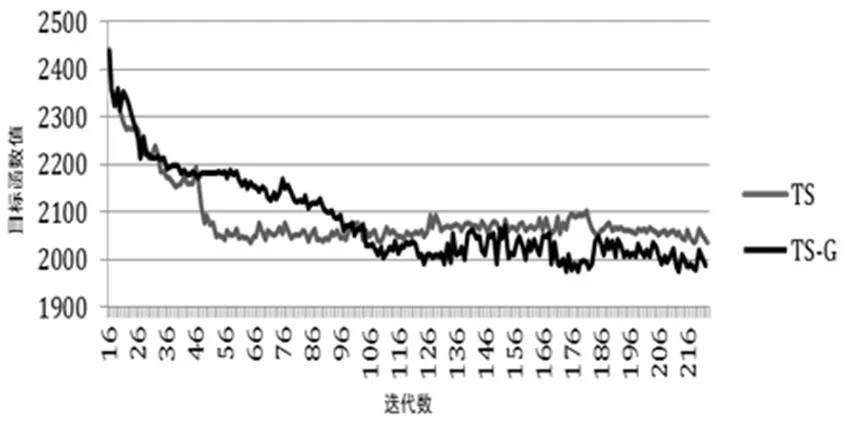
图2 导引机制的扩大算法搜索广度的能力展示

可见，由于没有导引机制的引导，标准TS很容易就困在局部最优解中无法逃离（为了让其运行足够久，标准TS下的设为100），与之形成鲜明对比的是，有导引机制的TS能有效避免过早地陷入局部最优解而将搜索引导到更宽广的空间，从而最终获得更优的解。在求解其它TC-8的问题时亦发现类似的鲜明对比。

4.2. 3不同效用函数对导引机制的影响

本文根据导引机制对固有属性信息与搜索历史信息的利用程度不同，定义了三种不同的效用函数“U1”, “U2”与“U3”。表3为在没有反应机制的前提下，不同效用函数对导引机制的影响，其均使用标准的惩罚方式。除效用函数与惩罚方式外，其它如初始解构造、邻域搜索与算法流程都与上文定义一致。表3中“OV”表示算法所能求得的最优解的目标值，“CPU”指其所需时间。

4.2. 4反应机制与导引机制求解TC-8算例的比较分析

由于HFFMCVRP的复杂性，即使是有“U2”导引机制的TS亦很难求得与HFFVRP已知最优解(BKS)足够接近的TC-8的解。因此，本文为检验两种机制是互相补充还是互相排斥，分别对RGTS、TS、有导引无反应机制的TS-G、有反应无导引机制的TS-R在求解TC-8问题进行比较。具体如表4所示。

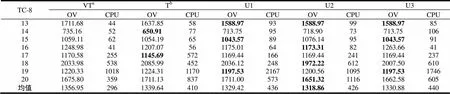
表 3 不同导引机制求解TC-8的比较

autility functionsbutility functionsTarantilis et al. (2008)

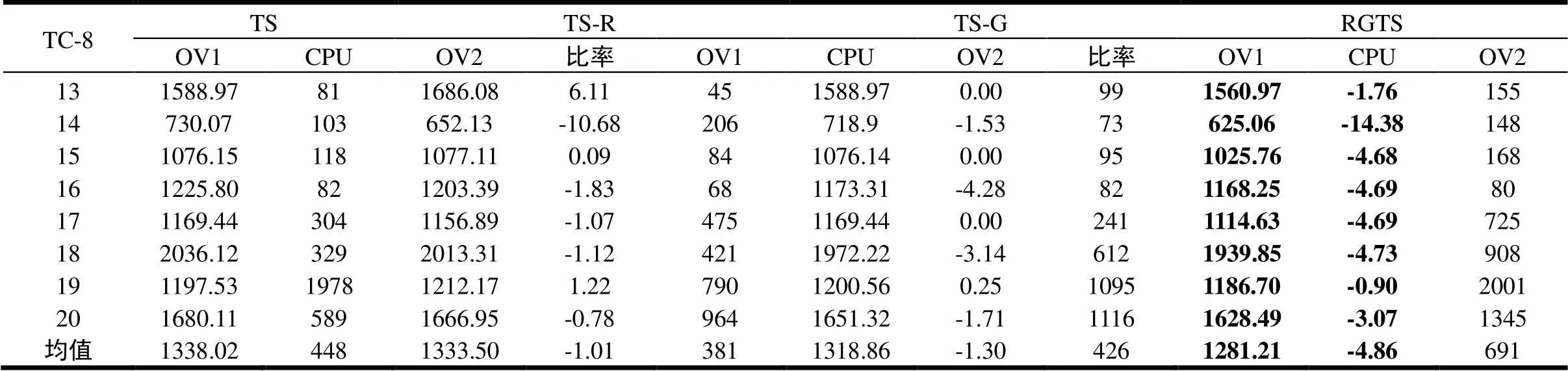
表 4 RGTS与TS-G及 TS-R 求解TC-8的比较

比率(%)：=100%*(OVi-OV1)/OV1

表4中RGTS求解效果最佳，表明反应与导引机制可相辅相成。上文提过HFFVRP的可行解可看作HFFMCVRP的可行解，故HFFVRP最优解可视为HFFMCVRP解的下界。

4.2. 5 RGTS与HFFVRP算法求解T-8的比较

与HFFVRP的标准算例T-8的已知最优解（BKS）相比，RGTS求得TC-8的解有一定距离，比率为4.06%，如表5所示。尽管这并非很小的比率，但由于TC-8算例远比T-8算例复杂，而且T-8的BKS是历经前人多次研究、通过精心编制的多种算法才获得的，所以比率属于可接受范围。

尽管RGTS并非针对HFFVRP设计的算法，但为进一步检验其鲁棒性，将其应用于求解T-8，并与HFFVRP的四个算法进行比较。根据表5的结果，RGTS具有一定的鲁棒性，因为它求得的最优解与T-8的BKS只有2.06%，等于(解-BKS)/BKS的距离。El- Fallahi 等[3]将其MCVRP算法应用于经典VRP时，其求得的最优解与经典VRP的BKS亦有1.02%的距离。他们认为使用 MCVRP算法求解VRP问题有一个困难，即在MCVRP框架下，VRP问题中虚拟的两个订单必须同时派送，这可能导致MCVRP算法在求解VRP问题时效率低下。从问题的继承性与困难度来看，本文中HFFMCVRP可对应MCVRP，而HFFVRP则对应经典VRP，因此El Fallahi 等[3]的解释亦适用于本文的情况。

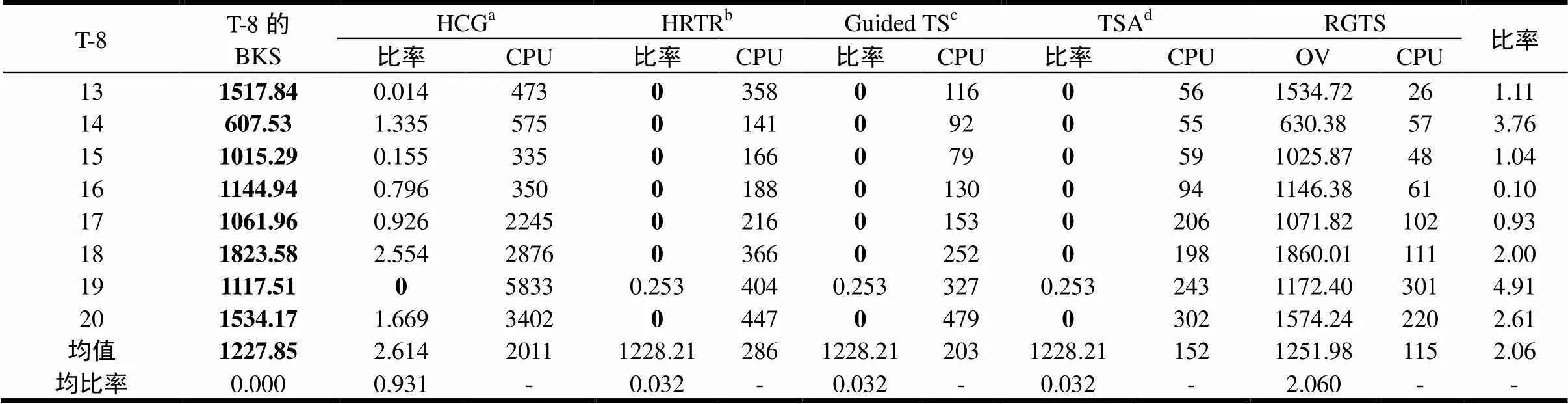
表 5 RGTS与HFFVRP算法求解T-8的比较

abcd

5 结论

本文围绕HFFMCVRP问题，提出一种混合的导引反应式禁忌搜索算法。为增强算法的寻优能力，该算法在求解过程中利用反应机制调整邻域范围参数以有效引导禁忌搜索的方向；同时改进的导引机制利用搜索过程的历史信息修正寻优过程中潜在的误导性。实验比较结果表明，本文提出的算法求解效果较优，在一定程度上实现深入搜索与多样搜索平衡。该研究成果在一定程度上扩展了VRP的理论研究，而且为燃油类、食品运输等实际HFFMCVRP应用企业的运营决策支持提供参考，具有理论与现实意义。

[1] Dantzig GB，Ramser JH. The truck dispatching problem[J]. Management Science，1959，6（1）：80-91.

[2] Muyldermans L，Pang G. On the benefits of co-collection: Experiments with a multi-compartment vehicle routing algorithm[J]. European Journal of Operational Research，2010，206：93-103.

[3] El-Fallahi A，Prins C，Calvo RW. A memetic algorithm and a tabu search for the multi-compartment vehicle routing problem[J]. Computers & Operations Research，2008，35：1725-1741.

[4] Derigs U，Gottlieb J，Kalkoff J et al. Vehicle routing with compartments: applications, modeling and heuristics[J]. OR Spectrum，2011，33（4）：885-914.

[5] Baldacci R，Battarra M，Vigo D. Routing a Heterogeneous Fleet of Vehicles[A].In： Golden BL，Raghavan S，Wasil EA. The Vehicle Routing Problem: Latest Advances and New Challenges [C]. New York：Springer，2008. 3-27.

[6] Taillard ED. A heuristic column generation method for the heterogeneous vehicle routing problem[J]. RAIRO，1999，33：1~14.

[7] Tarantilis CD，Kiranoudis CT. A meta-heuristic algorithm for the efficient distribution of perishable foods[J]. Journal of Food Engineering，2001，50：1-9.

[8] Tarantilis CD，Kiranoudis CT，Vassiliadis VS. A threshold accepting meta-heuristic for the heterogeneous fixed fleet vehicle routing problem[J]. European Journal of Operational Research，2004，152：148-158.

[9] Tarantilis CD，Kiranoudis CT. A List Based Threshold Accepting Meta-heuristic for the Heterogeneous Fixed Fleet Vehicle Routing Problem[J]. The Journal of the Operational Research Society，2003，54（1）：65-71.

[10] Tarantilis CD，Kiranoudis CT. A flexible adaptive memory-based algorithm for real-life transportation operations: Two case studies from dairy and construction sector[J]. European Journal of Operational Research，2007，179：806-822.

[11] Tarantilis CD，Zachariadis EE，Kiranoudis CT. A guided tabu search for the heterogeneous vehicle routing problem[J]. Journal of the Operational Research Society，2008，59：1659-1673.

[12] Li F，Golden B，Wasil E. A record-to-record travel algorithm for solving the heterogeneous fleet vehicle routing problem[J].Computers & Operations Research，2007，34：2734-2742.

[13] Li X，Tian P，Aneja YP. An adaptive memory programming metaheuristic for the heterogeneous fixed fleet vehicle routing problem[J]. Transportation Research Part E: Logistics and Transportation Review，2010，46（6）：1111-1127.

[14] Prindezis N，Kiranoudis CT. An internet-based logistics management system for enterprise chains[J]. Journal of Food Engineering，2005，70：373-381.

[15] Tütüncü GY. An interactive GRAMPS algorithm for the heterogeneous fixed fleet vehicle routing problem with and without backhauls[J]. European Journal of Operational Research，2010，201（2）：593-600.

[16] 郭耀煌，范莉莉，童淑惠. 多车型货运车辆优化调度[J].系统工程学报，1992，7（1）：111-117.

[17] 李嘉，王梦光，唐立新，等.一类特殊车辆路径问题(VRP)[J].东北大学学报(自然科学版)，2001，22（3）：245-248.

[18] 袁庆达，杜文，周再玲. 带软时间窗的混合车队车辆路线问题的模型和算法研究[J].西南交通大学学报，2001，36（4）：401-406.

[19] 李建，张永，达庆利.第三方物流多车型硬时间窗路线问题研究[J].系统工程学报，2008，23（1）：74-80.

[20] 郑丽英，贾海鹏.全局搜索聚类的多车场多车型调度算法研究[J].兰州交通大学学报，2009，28（6）：19-22.

[21] 王晓博，李一军.多车场多车型装卸混合车辆路径问题研究[J].控制与决策，2009，24（12）：1769-1774.

[22] 戴锡，叶耀华，吴勤旻，等. 油品配送车辆路径问题的交互式求解方法[J]. 系统工程学报，2009，24（6）：749-753.

[23] Glover F，Kochenberger GA，Alidaee B. Adaptive Memory Tabu Search for Binary Quadratic Programs[J]. Management Science，1998，44（3）：336-345.

[24] Battiti R，Tecchiolli G. The reactive tabu search[J]. ORSA Journal on Computing，1994，6：126-140.

[25] Osman IH，Wassan NA. A reactive tabu search meta-heuristic for the vehicle routing problem with backhauls[J]. Journal of Scheduling，2002，5：263-285.

[26] Wassan NA，Osman IH. Tabu search variants for the mix fleet vehicle routing problem[J]. The Journal of the Operational Research Society，2002，53：768-782.

[27] Wassan NA. A reactive tabu search for the vehicle routing problem[J]. The Journal of the Operational Research Society，2006，57：111-116.

[28] Wassan NA，Wassan AH，Nagy G. A reactive tabu search algorithm for the vehicle routing problem with simultaneous pickups and deliveries[J]. Journal of Combinatorial Optimization，2008，15：368-386.

A Hybrid Guided Reactive Tabu Search for Heterogeneous Fixed Fleet Multi-compartment Vehicle Routing Problem

WANG Qian1, JI Qing-kai2,1, HU Xiang-pei2

(1. Sun Yat-sen Business School, Sun Yat-sen University, Guangzhou 510275, China;2. Institute of System Engineering, Dalian University of Technology, Dalian 510275, China)

Heterogeneous fixed fleet multi-compartment vehicle routing problem (HFFMCVRP) prevails in industries such as oil and food industries. Such real life problems have not been well studied by scholars. In this paper, we propose a three-index mathematical model that can well characterize the features of multi-compartment and heterogeneous fleet. We then incorporate the reactive mechanism and guiding mechanism when designing the hybrid guided reactive tabu search (RGTS) to solve HFFMCVRP. By adapting the tabu list size and the neighborhood size according to search performance (i.e., generally speaking, shortening the tabu list size and increasing the neighborhood size when the search returns a series of new solutions, while lengthening the tabu list size and reducing the neighborhood size while the search returns many repetitions), the RGTS successfully utilize the upgraded reactive mechanism to increase the tabu search’s flexibility. More importantly, to decrease the chance of “misleading” during the classic guided search, an enhanced guiding mechanism is introduced into RGTS by efficiently applying history information of the search. More specifically, the utility function of our guiding mechanism is based on a continuously-updated matrix which records the appearance of edges in good solutions returned by the search. As a result, the selection of edge according to the utility function for penalization is more reasonable. Several well-known neighborhood operators including 2-1 move, 1-1 move, 1-0 move, 2-opt*, swap, relocate and 2-opt, are applied in the search. As for experimentation, since there is no public HFFMCVRP instance set, we derive instance set TC-8 by besetting the benchmark instance set T-8 of the heterogeneous fixed fleet vehicle routing problem (HFFVRP). Vehicles and orders in T-8 are “bisected” so that there are two compartments for each vehicle and two orders for each customer in TC-8. The first/second order of each customer can only be carried in the first/second compartment of vehicles. Firstly, three different guiding mechanisms characterized by different utility functions are numerically compared to assess their effectiveness. Our guiding mechanism with the utilization of search history information dominates others with only predetermined information (i.e. distances of edges). Secondly, the tabu search, the tabu search with reactive mechanism, the tabu search with guding mechanism and the tabu search with both mechanisms (i.e. RGTS) are compared to justify these two hybrid mechanisms. RGTS outperforms others by producing better solutions. Thirdly, in order to test the robustness of RGTS, we apply it to solve the heterogeneous fixed fleet vehicle routing problem (HFFVRP), even though RGTS is not specifically designed for HFFVRP. The results indicate that RGTS can produce solutions of an average gap 2.06% compared to the best-known solution of HFFVRP benchmark instances, which is acceptable since HFFMCVRP is much harder than HFFVRP. In summary, experiments demonstrate that our heuristic can dynamically balance the intensification and diversification of the search through the reactive mechanism and guiding mechanism in order to efficiently solve the complex HFFMCVRP.

multi-compartment; heterogeneous fleet; guiding mechanism; reactive mechanism; tabu search.

中文编辑：杜 健；英文编辑：Charlie C. Chen

U16

A

1004-6062(2016)03-0179-09

10.13587/j.cnki.jieem.2016.03.022

2013-09-28

2015-12-22

国家自然科学基金资助项目（70971141）；国家自然科学基金重点资助项目（71431007）

王茜（1971—），女，辽宁丹东人；中山大学管理学院教授，博士生导师，研究方向：电子商务，网络信息战略，物流管理。