基于需求依赖库存的多制造商供应链博弈与协调模型

付 娟，闵 杰，赵 菊，欧 剑



基于需求依赖库存的多制造商供应链博弈与协调模型

付 娟1，闵 杰2，赵 菊3，欧 剑2

(1.安徽建筑大学管理学院，安徽合肥，230601；2.安徽建筑大学数理学院，安徽合肥，230601；3.合肥工业大学管理学院，安徽合肥，230009)

考虑一个具有决策优先优势的零售商，如大型超市，同时销售两个制造商的同类产品，研究了这类两层非一体化供应链的博弈和协调问题。假设商品需求依赖自己的库存展示水平和竞争对手的库存水平。博弈过程中，零售商是决策的先行动者，首先宣布库存展示策略，两个制造商作为跟随者，然后决定相应的策略。根据两个制造商决策顺序的不同，建立了两个模型，一个是两制造商同时反应的Nash均衡博弈；另一个是两制造商先后反应的Stackelberg主从博弈。分析了制造商及其竞争对手的库存量对需求的影响和供应链各方利润变化情况，得到了一些管理启示。另外，给出了量折扣策略实现供应链协调。最后，数值算例结果验证了该模型的有效性。

需求依赖库存; 供应链；博弈; 协调

0 引言

很多模型已经考虑了多零售商的竞争对供应链决策的影响，但考虑上层制造商之间的竞争对供应链决策影响的研究不是很多。而实际中在不同的市场领域存在很多同类产品，例如饮料市场上的百事可乐和可口可乐，日化用品市场上的宝洁和联合利华等，这些由不同制造商所生产的同类产品会在同一零售商如沃尔玛出售。传统的供应链中制造商（或者供应商）占据着主导地位，但近年来供应链中的很多研究已经表明，在零售业供应链中零售商的影响力已经有所增加，甚至占据主导地位，如零售巨头沃尔玛，便利之王7-11。因此，零售商利用其优势地位使得制造商配合其库存展示策略，并且决定各种产品的库存展示量。而作为决策跟随者的多个制造商间往往要展开博弈或者合作，所以研究在零售商主导下多制造商供应链的协调与优化问题具有很强的实际意义。

考虑到现实中的零售业供应链销售终端大多是超市型卖场，而市场营销研究者Levin等人[1]、Assuncao等人[2]和Balakrishnan等人[3]发现，在超市型的销售终端中库存的展现常常对周围的人产生激励性的影响，在超市里向顾客展示的产品数量越多，就能吸引更多的顾客，这就是所谓的需求依赖库存模式。因此，许多学者对需求依赖库存的供应链优化问题展开了研究。

近期比较具有代表性研究是从零售商的角度研究的库存模型。一部分学者的研究是基于假设需求与展示的最高库存量有关。Alfares[4]通过考虑单位产品的库存费为存贮时间的函数而建立了相应的库存模型，但是此模型假设库存周期结束时系统的剩余库存水平为零，Urban[5]在模型中设想周期结束时剩余库存非零，以平均利润最大化重新研究了上述模型，得到了一些有意义的结论。徐贤浩和李锐娟[6]建立了存货影响销售率的短生命周期产品的库存模型，适用于电子元件、计算机、彩电、空调等产品。李根道等人[7]假设需求受库存水平影响建立了相应的库存模型，并利用Monte-Carlo模拟对文中所得价格策略和以往的研究中不考虑库存影响得到的价格策略进行比较，说明在制定决策时考虑库存对需求的影响的重要性。与以往文献研究单物品不同，Stavrulaki[8]针对两种可以互相替代的产品研究了需求依赖库存情形下的库存决策模型，研究表明通过运用必要的销售信息，量化替代和需求刺激能够产生较高利润。另有一些研究是基于假设产品的需求线性依赖于销售店铺当前的库存水平的。Goyal和Chang[9]在有最小库存展示量的条件下（当库存水平下降到一定量立即从货栈中心运送产品到达店铺），构造了平均利润最大化的库存模型，并提供了求解算法。Min和Zhou[10]研究了有存储空间限制的情况下短缺部分拖后的库存模型，其中需求拖后率与当时已经发生的缺货量有关。Chang等人[11]研究了短缺部分拖后的非立即变质性产品的库存模型。莫降涛等人[12]研究了易变质多产品库存问题，在总库存容量有限的条件下，以优化库存系统的平均成本为目标，建立相应的库存优化模型。Hsieh等人[13]则假设只有当库存高于一定水平时商品需求才依赖于库存而研究了相应的库存问题。

然而，以上这些研究通常从零售商的角度考虑了单节点企业的库存控制问题。Wang和Gerchak[14]首次讨论了需求受零售商库存展示水平影响下单制造商-单零售商和单制造商-多零售商的供应链协调问题，其协调手段是一种“价格+库存线性补贴”策略。但是需求依赖库存环境下多制造商-单零售商供应链管理领域的研究却鲜有报道。本文将针对需求受零售商库存水平影响的情形，研究由两个相互竞争的制造商和单个零售商组成的两层非一体化的供应链协调问题。在此供应链中，因为零售商往往能得到更多的消费者需求信息，从而能更准确地确定需求量，在这种情况下零售商处于主导地位，所以零售商首先宣布库存展示策略，制造商然后做出相应的策略。根据两个制造商决策顺序的不同，本文发展了两个不同的供应链博弈模型，第一个模型是当零售商提出库存策略时，两个制造商相互独立且同时反应；第二个模型则描述了面对零售商提出的策略，两个制造商是主从的竞争关系。通过讨论制造商及其竞争对手的库存量对该产品需求的影响和各方利润分析，分别给出了区别于价格和库存补贴的供应链协调手段—量折扣策略，最后用实例说明了模型的应用。

1 问题描述及符号与假设

考虑一个零售商，例如大型超市，同时销售两个制造商的同类产品。两制造商的产品需求受零售商库存水平影响。因此两制造商竞争展示库存水平，以增加利润。博弈过程中，零售商是决策的先行动者，首先宣布库存展示策略，两个制造商作为跟随者，然后做出相应的策略。两个制造商决策顺序有两种可能，一是当零售商提出库存策略时，两个制造商相互独立且同时反应；二是面对零售商提出的策略，两个制造商是主从的竞争关系。

模型假设：

（1）市场营销学研究者Levin等人(1972)[1]发现销售终端中商品展示水平的“选择效应”和“广告效应”，使得商品需求在很大程度上依赖其库存水平。所以本文假设产品的需求函数为以下形式：

其中，D表示市场需求，I表示第种产品的库存展示量。表示库存水平为零时的需求量,表示需求对本身库存的敏感度,表示需求对另一种同类品牌的库存敏感度，即市场需求在受到本身库存激励的同时也会受到其他同类产品库存的正面影响；

（2）考虑由两个制造商和单个零售商组成的两层供应链，其中两个制造商分别批发同一种但不同品牌的产品给同一零售商，由于类似沃尔玛、家乐福等大型零售企业在市场上往往处于主导地位，所以假定零售商为该供应链的核心主导企业，决定产品的库存展示水平I；

（3）由于市场价格属于商业机密，所以假设两制造商只能观测到对方产品在零售商处的库存展示水平，而不清楚对方批发产品给零售商的价格w；

（4）考虑到产品零售价格(p)高于批发价格(w)，而批发价格又高于生产成本(c)，所以假设p>w>c，其中p，c为固定的常数，而w是制造商需要决策的变量；

（5）由于零售商销售两种同类产品，市场销售价格差别不大，因此对于批发价格较低的产品零售商自然会给予较多的展示空间以促进销售，即零售商对每种产品库存展示水平的决策与制造商所提供的批发价格有关，所以本文假设I=-nw, 其中>0,>0.

符号变量：

2 模型构建

根据制造商之间的博弈关系不同，本文基于需求依赖库存发展两个供应链博弈模型，并分别给出相应的协调优化策略。第一个模型假设两个制造商面对零售商的策略相互独立且同时反应。第二个模型则假设两个制造商之间存在一种主从关系。两个模型都是假设零售商在供应链中处于主导地位。

2.1 两个相互竞争的制造商同时反应的模型

本文首先考虑由两个相互竞争的制造商和一个零售商组成的两层供应链结构。由两个不同的制造商生产的产品对消费者存在某种程度的互补性。两层供应链中的相互作用机制是这样一个过程，即零售商是主导者，两个制造商是跟随者。零售商参考制造商的批发价格(w)决定其生产商品的库存展示水平（I）。

由于零售商在供应链博弈中处于主导地位，根据斯坦伯格博弈过程，首先向两个制造商宣布自己的购买量或者需求量，然后两个制造商独立且同时反应，给出其批发价格w。两个制造商的利润函数可以用以下形式表示：

（3）

=（5）

从零售商的角度看，因为她处于主导地位，所以知道制造商的反应函数，并且她也要最大化自己的利润。而零售商的利润函数可以用以下形式表示：

（7）

再将(7)、(8)式代入(4) 、(5)式，则可以得到每个制造商的最优批发价格为：

（9）

（10）

将(7)、(8)式代入(1)，从而得到每种产品的生产量或者需求量为

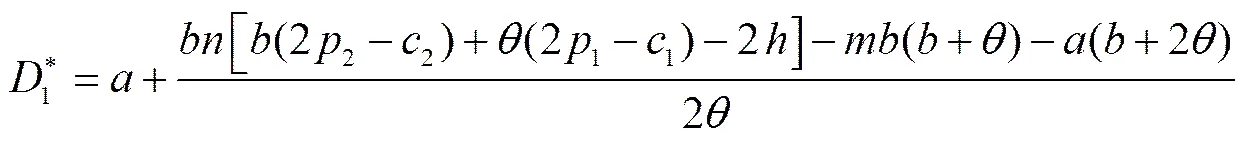
（12）

如同能得到(7)-(12)式，同样能解出两个制造商的利润，，以及零售商的利润，本文将在下一节中通过数值例子给出具体分析。

2.2 两个相互竞争的制造商有主从关系的模型

在第二个模型中，本文假设其中一个制造商（例如，制造商1）处于主导地位，另一个制造商处于从属地位（例如，制造商2）。根据动态博弈的逆推归纳法，对于任意给定的1，2和，跟随方（制造商2）通过一阶最优条件，得到最优的批发价格，其值为

制造商1要根据其竞争对手所给批发价格，最大化其自身利润，将(13)式代入(2)式并使得，可以得到的最优值为

（14）

同样，零售商知道制造商的决策并将最大化自己的利润，通过将（13）、（14）式代入零售商的利润函数(6)式并求解和，就可求得零售商关于两种商品库存量的最优策略1*，2*分别为

（16）

将(15)、(16)式代入(13)、(14)，可以得到每个制造商的最优批发价格为

（18）

同样，可以求得制造商1和制造商2的生产量或者产品的需求量和，以及两个制造商和零售商的利润，，。

3博弈模型分析

本节将通过数值例子来讨论各种情形下供应链各成员库存量（1*，2*）和批发价格w*的决策。模型中的参数取值为：=1.5,=0.4,=3.8,=3.8,=2,=2,=10,=5,=0.9.

为了检测以上模型中制造商本身产品库存量对该产品需求量的影响度和竞争对手的库存量对该产品需求量的影响度对模型的影响，本文通过调整,的值来观察实验结果，其余参数保持不变并且假设两个制造商有相同的生产成本。

3.1 对的讨论

表1给出了变化的情况下，两个模型中的最优库存量1*，2*和最优批发价格1*，2*以及该状态下的需求量的有关数据结果。第一个模型中，两个制造商面对零售商的策略时相互独立且同时反应，从表1中可看出，同一下，零售商对两种产品的最优库存量和两个制造商给予零售商的批发价格都相等。但是，第二个模型中，处于跟随地位的制造商比处于主导地位的制造商占优势，当零售商给予两种产品相同的销售价格时，跟随方的批发价格却高于主导方，其库存展示量也多于主导方，这会吸引更多的需求。还可以看出，第一个模型中，当增大即自身库存量对自身需求影响度增加时，零售商对两种产品的库存量都在增加，而且此时两个制造商对零售商的批发价格也都在增大，由此可见两种产品的需求量的增加，使得零售商在批发价格上升的情况下还要增加库存。第二个模型中，随着自身库存影响度的增大，两种产品的库存展示量都有所增加，但不同于第一个模型的是，占主导地位制造商的库存展示量小于跟随方的库存展示量，其需求量也低于跟随方，且二者之间的需求量之差有随着的增加而逐渐增大的趋势。换句话说，当自身库存对需求的影响增大时，消费者更倾向于展出量较多者，这与顾客在商店选购商品时的消费行为一致。在实际生活中，沃尔玛、家乐福等大型超市的顾客总是倾向在展示物品量多、广告力度大的商品中挑选商品，比如百事可乐和可口可乐这两种同类产品，由于可口可乐展示商品量大，因此销售量也高于百事可乐，这也进一步验证了本文的研究结论。

表1 不同的b值下两个模型的展出量、批发价格及需求量的最优解

图1 不同b下同等地位模型的库存展示量、批发价格及需求量的最优解

在上面计算结果的基础上，供应链各方利润情况如表2所示。供应链中每个成员的利润表示为，，，三者的利润之和表示为，跟随方与主导方的利润之比表示为，零售商占总利润的百分比表示为。

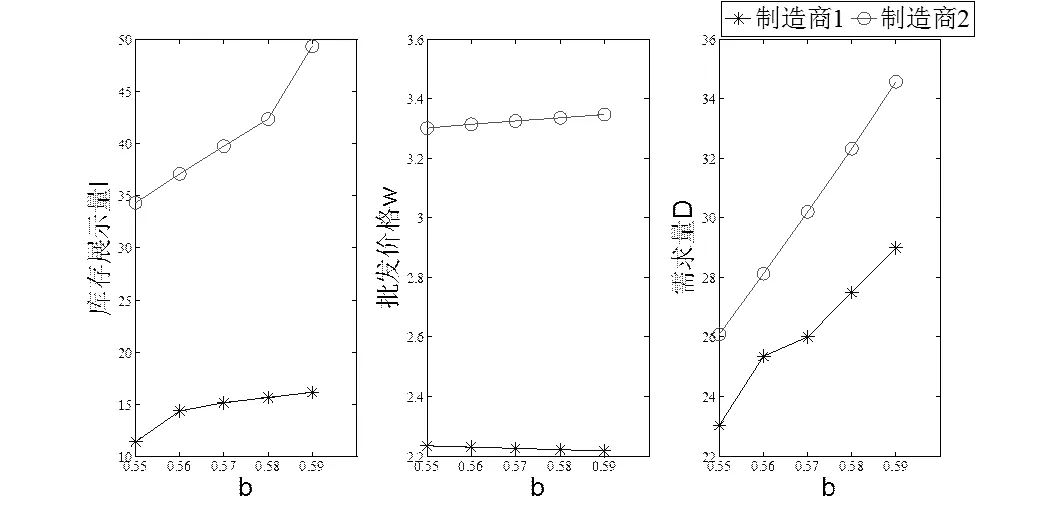
图2 不同b下主从关系模型的库存展示量、批发价格及需求量的最优解

表2 不同b下，两个模型中的各方利润

图3 不同b下同等地位模型的各方利润

从表2可看出，各方的利润及总利润也随着的变化而变化。第一个模型中，随着的增大，各方及总利润都在增加，零售商在总利润中所占比例却在减小，但始终高于两个制造商的利润，可见零售商的主导地位。还可看出，产品需求对库存的依赖越大，对制造商越是有利。第二个模型中，随着的增大，各方利润和总利润也在相应增加，但明显跟随方的利润高于零售商，而零售商的利润又高于主导方，且零售商在总利润中所占比例在减小，跟随方与主导方的利润之差越来越大。总之，本产品的库存对该产品的需求影响度的增大能增加供应链的整体利润，尤其对制造商有利。在两个制造商中虽然主导方处于强势，但是需要先决策，而从属方虽然处于弱势，但是需要后决策。根据博弈论的经典内容，后决策的一方具有后动优势，往往在收益方面占据更多的份额。

图4 不同b下主从关系模型的各方利润

3.2 对的讨论

表3给出了变化的情况下，两个模型中的最优库存量1*，2*和最优批发价格1*，2*以及该状态下的需求量的有关数据结果。模型的参数取值如下：=1.5,=0.6,=3.8,=3.8,=2,=2,=10,=5,=0.9.

表3 不同q下的两个模型的库存展示量、批发价格及需求量的最优解

图5 不同q下同等地位模型的库存展示量、批发价格及需求量的最优解

图6 不同q下主从关系模型的库存展示量、批发价格及需求量的最优解

从表3中可看出，第一个模型中由于两个制造商面对零售商的策略时独立且同时反应，同一值下二者的最优库存量和批发价格都相等。但是在第二个模型中，处于跟随地位的制造商比处于主导地位的制造商占优势，当零售商给予两种产品相同的销售价格时，跟随方的批发价格却高于主导方，其库存展示量也多于主导方。另外，第一个模型中，当增大时即自身库存对竞争对手的需求影响度增大时，两种产品的需求在减小，零售商对两种产品的库存量在减少，制造商批发给零售商的批发价格也在减少。可见需求量的减小，使得零售商减小了库存，从而迫使制造商降低批发价格来吸引零售商。第二个模型与第一个模型的不同之处在于批发价格随着的增加也增加，这点很有趣，可能是由于订购量的减少使得制造商不能给予优惠。

一旦最优库存展示量给出，供应链各方利润情况如表4所示。从表4中可看出，第一个模型中，随着的增大，两个制造商的利润都在减少，但零售商的利润和三者的总利润都在增加，可见的增大对零售商有利。第二个模型中，随着的增大，各方的利润都在减少，但跟随方的利润高于零售商，零售商的利润又高于主导方，且零售商在总利润中所占比例在增加，主导方与跟随方的利润差距在缩小。总之,越大对制造商越不利。

表4 不同q下两个模型中的各方利润

图7 不同q下同等地位模型的各方利润

图8 不同q下主从关系模型的各方利润

4 供应链协调策略

通过上面分析可知由于供应链各成员都是各自为政，所以整个供应链处于一种失调状态。为了提高供应链的效率，可以为占据供应链主导地位的零售商设计如下协调策略：

其中>1,0<r<1，

由于在该协调策略中，若制造商的批发价格达不到“资格”得到优惠展出量kI*，制造商仍然享受原有的正常产品展出量，因此该策略并不损害制造商的利益。但同时若要使得制造商乐意接受此策略，必须要保证其利润还要有一定的增加。本文假设只有在制造商的利润增量的百分比至少为的时候此策略才会被接受。可见该策略如果还能提高零售商及其供应链的整体利润，那么它将是合理的、可行的。下面将给出该策略的设计过程。

在此策略下，制造商的利润函数为：

（20）

零售商的利润函数为：

（22）

下面本文通过一个例子来说明此供应链协调策略在实际中的应用。

表5 两个模型中协调前后的各方利润比较

图9 不同b下同等地位模型协调前后的各方利润

图10 不同b下主从关系模型协调前后的各方利润

5结束语

现实中商品的库存水平影响需求是普遍的现象，这意味着零售企业的订货决策会影响商品的销售，最终也会影响商品制造企业的利润。因此供应链需要能够根据需求随库存水平的实际变化情况适时地科学地制订激励契约，以诱使零售商加大订货量来刺激更多的潜在需求，但已有的相关研究成果（通常忽略库存水平对需求的正向影响）没有很好解决这一问题。本文利用库存水平拟弹性需求函数去逼近产品的实际需求，研究了需求受库存影响下由两个相互竞争的制造商和一个占据主导地位的零售商所组成的两层供应链的协调问题，主要讨论了两个制造商之间的不同竞争形式下制造商与零售商之间的博弈情况，给出了相应的决策模型和方法，并且为供应链设计了可行的协调策略-量折扣机制，为实际企业的供应链管理提供了决策参考。但是本文考虑的是确定性需求情况，而事实上随机性需求现象在实际生活中大量存在，因此未来模型进一步的拓展方向之一是在随机需求环境下对复杂供应链协调问题展开研究。

[1] Levin R I, McLaughlin C P, Lamone R P, Kottas J F. Production / Operations Management: Contemporary Policy for Managing Operating Systems[M]. New York:McGraw-Hill, 1972: 1- 229.

[2] Assuncao J L, Meyer R J. The rational effect of price promotions on sales and consumption[J]. ManagementScience, 1993, 39(5): 517– 535.

[3] Balakrishnan A, Pangburn M S, Stavrulaki E. “Stack them high, let 'em fly”: lot-sizing policies when inventories stimulate demand[J]. Management Science, 2004, 50(5): 630–644.

[4] Alfares H K. Inventory model with stock-level dependent demand rate and variable holding cost [J]. International Journal of Production Economics, 2007, 108(1-2): 259–265.

[5] Urban T L. An extension of inventory models with discretely variable holding costs [J]. International Journal of Production Economics, 2008, 114(1): 399–403.

[6] 徐贤浩,李锐娟. 存货影响销售率的短生命周期产品库存管理[J].系统管理学报,2007, 16(2): 135– 138.

[7] 李根道,熊中楷,聂佳佳. 库存和价格影响需求的易逝品动态定价[J].系统管理学报,2009, 18(4): 402– 409.

[8] Stavrulaki E. Inventory decisions for substitutable products with stock-dependent demand [J]. International Journal of Production Economics, 2011, 129(1): 65–78.

[9] Goyal S K, Chang C T. Optimal ordering and transfer policy for an inventory with stock dependent demand [J]. European Journal of Operational Research, 2009, 196(1): 177–185.

[10] Min J, Zhou Y W. A perishable inventory model under stock-dependent selling rate and shortage- dependent partial backlogging with capacity constraint[J]. International Journal of Systems Science, 2009, 40(1): 33–44.

[11] Chang C T, Goyal S K, Teng J T. Optimal replenishment policies for non-instantaneous deteriorating items with stock-dependent demand [J].International Journal of Production Economics, 2010, 123(1): 62–68.

[12] 莫降涛,陈桂梅,范婷,毛宏. 需求依赖即时库存水平的易变质多产品最优订购策略[J].系统工程,2011,29(5): 98-101.

[13] Hsieh T P, Dye C Y, Ouyang L Y. Optimal lot size for an item with partial backlogging rate when demand is stimulated by inventory above a certain stock level [J]. Mathematical and Computer Modelling, 2010, 51(1-2): 13–32.

[14] Wang Y, Gerchak, Y. Supply chain coordination when demand is shelf-space dependent[J]. Manufacturing and Service Operations Management, 2001, 3 (1): 82–87.

Game and Coordination Models for Supply Chains with Multiple Manufacturers under Inventory-Dependent Demand

FU Juan1,MIN Jie2,ZHAO Ju3, OU Jian2

(1.School of Management, Anhui Jianzhu University, Hefei230601, China; 2.Department of Mathematics& Physics, Anhui Jianzhu University, Hefei230601, China;3. School of Management, Hefei University of Technology, Hefei 230009,China)

This paper considers the game and coordination issues of a two-echelon supply chain consisted of two manufacturers and a dominant retailer, such as supermarket. Two manufacturers produce similar items and sell them by the same retailer. Assume that the demand of each item is not only dependent on its own inventory level displayed on shelf but also on its competitor’s. Therefore, the two manufacturers compete for the same shelf space. First，the retailer declares its shelf display policy. The two manufacturers, as followers, then make their actions. According to the different order of making decision, two supply chain game models are developed, namely Nash equilibrium game, in which they take actions at same time, and Stackelberg game, in which they take actions in sequence. We then analyze the effect of a manufacturer’s own and its competitor’s inventories on production’s sale rate and profit of supply chain players. Some managerial insights are shown as follows: (1) With the increasing of the impact factor of its own inventory on the demand (denoted by), both the displayed quantities and the demands of the two productions increase, and the wholesale prices also increase. (2) The increasing ofwill benefit the supply chain as a whole, especially for manufacturers. (3) With the increasing of the impact factor of its competitor’s inventory on the demand (denoted by), both the displayed quantities and the demands decrease. The wholesale prices decrease in Nash game but increase in Stackelberg game. (4) The increasing ofwill be unfavorable for manufacturers. (5) The late-mover advantage is proven. In addition, quantity discount policy is given to coordinate the supply chain. Numerical examples show that the models are considerable effective in improving supply chain efficiency and coordinating supply chains.

inventory-level-dependent demand; delay in payments; supply chain coordination

中文编辑：杜 健；英文编辑：Charlie C. Chen

O221

A

1004-6062(2016)03-0195-07

10.13587/j.cnki.jieem.2016.03.024

2013-01-27

2014-03-11

国家自然科学基金资助项目（71101002，71201044，71072165）；合肥工业大学博士学位专项基金资助项目（2012HGBZ0197）

付娟(1990—)，女，安徽庐江人，硕士研究生，主要从事库存控制理论和供应链管理研究。