中国金属期货市场高频波动率预测模型比较研究

陈晓东



中国金属期货市场高频波动率预测模型比较研究

陈晓东

（重庆文理学院数学与财经学院，重庆，402160）

文章选取上海期货交易所铜、铝期货价格指数日内10分钟高频收益数据，构造了经调整的已实现极差波动率估计序列，利用6类GARCH族模型建模分析，描述了沪铜、沪铝期货价格指数的波动特征。运用多种损失函数比较了GARCH族模型样本外波动率预测精度的优劣，并在此基础上，采用Diebold－Mariano检验法评估了GARCH族模型的预测效果。结果显示，沪铜、沪铝期货市场上已实现极差波动率估计序列具有尖峰厚尾、集聚性、持续性等特征。对于沪铜期货市场，EGARCH模型具有相对较好的的波动率预测能力，在某些损失函数标准下，FIGARCH模型以及GJR模型也体现出了较好的波动率预测能力，但FIGARCH模型的预测能力和其它模型相比较并不显著；对于沪铝期货市场，EGARCH和HYGARCH模型具有相对较好的的波动率预测能力，而在某些损失函数标准下，FIGARCH以及IGARCH模型也体现出了较好的波动率预测能力。

金属期货；波动率；GARCH模型；DM检验

0引言

作为重要的金属品种，铜和铝被广泛应用到了电子电器、机械、建筑、国防等多个领域，在我国经济发展中起着重要的作用。自90年代改革开放以来，铜、铝消费便进入了一个快速发展时期，经济增长的高速化、基础建设的规模化都是促进铜、铝消费快速增长的主要原因。2001年，我国成为世界最大铝生产和消费国；2002年，我国成为超越美国的最大铜消费国。而随着西方发达国家逐步把制造业向新兴发展中国家转移，我国铜、铝消费还会进一步快速增长。我国有大量铜、铝消费和生产企业，这些企业都有套期保值的迫切需要。因此，自上海期货交易所成立以来，铜、铝便成为金属期货市场最主要的交易品种，而沪铜期货合约也是我国目前交易最为活跃的合约之一。2008年，随着全球金融危机的全面爆发，国际铜、铝价格出现了巨幅波动，也自然波及到了商品期货,对我国金属期货市场产生了较大冲击。铜、铝期货价格不仅会受到国际国内经济形势的影响，还会受到汇率、进出口政策、、基金的交易方向等因素影响。随着影响因素的不断增多,铜、铝期货价格出现剧烈波动的特征也越发明显，把握铜、铝期货价格的波动特征,对期货市场进行更好的风险管理则显得尤为突出。

目前，学者们针对金属期货市场的价格波动描述和模型预测进行了相关的研究。郑丰，崔积钰，马志伟(2013)[1]应用自相关函数检验法和GARCH模型检验方法，对沪铜期货收益率序列进行实证研究，通过移动窗口法引入了波动聚集指数度量沪铜期货市场的波动聚集程度，并对其波动聚集的相关特征做了研究。结果表明不同时间标度的沪铜连续合约收益率序列都存在波动聚集现象，铜期货表现出自相似的特征，沪铜期货市场具有分形特征，存在记忆性。朱学红, 沈玉芳, 邵留国(2012)[2]采用三个GARCH族中的两因素波动模型研究金、铜和铝在原油和汇率冲击下的价格波动行为。标准GARCH模型的结果表明铜和铝几乎有着一样的波动持续性且都比金的波动持续性强。CGARCH模型估计结果表明三种金属波动的短期成分收敛到0的速度由快到慢依次为: 铝、金、铜。EGARCH结果表明只有铜存在杠杆效应而且显著。石油冲击对三种金属都有正影响, 汇率的上升对金、铜和铝的波动都有减弱效应。武琳,丁浩（2012）[3]通过Granger因果检验法分析了国内外主要市场铜期货价格与国内铜现货价格间的长期均衡关系，通过建立误差修正模型和方差分解方法研究了铜期货波动对国内铜现货的价格引导作用。结果表明铜期货现货价格之间存在长期均衡关系。程慧,黄健柏,郭尧琦(2012)[4]采用V统计量和经验模态分解方法，以铜、铝价格为例实证分析我国有色金属价格波动的周期性特征，并根据研究结论提出相关对策建议，以期能够规避有色金属价格周期性波动对工业及国民经济带来的不利影响。崔海蓉,何建敏,张京波(2012)[5]以上海期货交易所的期铜和期铝为例，运用多变量GARCH-BEKK模型研究了我国有色金属期货之间的波动溢出关系，并分别在标准残差服从正态分布和学生t-分布假设下，进行模型拟合效果检验。研究结果表明，期铜和期铝收益率序列存在显著的条件异方差特征，两者之间存在较强的双向波动溢出效应，t-分布假设下GARCH-BEKK模型拟合效果更好。李丹宁和穆铮等（2012）[6]针对非参数模型的三种估计方法，将其应用于沪铜期价与LME现价的相关关系分析。最后与最小二乘法的结果进行比较分析，证实了非参数估计在不同历史时期有预测精度高的优点。张保银和陈俊（2012）[7]通过采用ADF 检验、协整性检验及Granger因果检验对近年来上海铜期货市场的价格发现功能进行全面深入的动态实证分析，表明铜期货价格具有良好的价格发现功能。通过动态向量误差修正模型检验，铜现货市场和期货市场价格波动相关性趋于加强，但呈现出非线性规律，说明企业在进行套期保值决策时能以期货价格波动作为决策依据之一，但不能对期货价格波动反应过度，致使套期保值行为失当，需要综合分析外部市场环境和期货市场运行规律，做出全面科学的套期保值决策。胡龙和胡太军（2011）[8]对上证指数和沪铜指数分别进行了平稳性检验、协整关系检验。并运用VECM 模型和二元GARCH 模型对二者是否存在联动关系以及存在怎样的联动关系进行了实证分析。结果表明，上证指数和沪铜指数的波动在短期内的关系并不明显，但在长期二者之间有着很强的相关性，而且这种关联性随着时间的推移呈现出越来越强的态势。王泰强，侯光明，赵宏（2011）[9]利用GARCH模型和半参数方法对上海期货交易所铝期货和铜期货的市场风险进行了测度。研究结果表明，沪铝期货和沪铜期货收益率序列不服从正态分布，具有尖峰厚尾、波动聚集的特征；沪铝期货的市场风险较沪铜期货更小。李莎姗(2010)[10]采用了GARCH族模型来描述沪铜期货市场收益率数据的条件异方差性，并对期铜市场的风险溢价和杠杆效应进行检验。结论表明我国沪铜期货市场存在明显的波动聚集性和时间可变性，不存在明显的风险溢价。方燕和庞小利(2010)[11]主要从铜期货与现货价格的变动关系出发，研究两者的走势特征，得出了沪铜期货价格与现货价格之间在长期和短期不同的影响系数的结论。赵伟雄，崔海蓉，何建敏(2010)[12]以沪铜期货为例，研究了4类GARCH模型的波动率预测效果。采用M-Z回归和损失函数进行预测效果检验，结果表明4类GARCH模型预测效果有显著差异。方伟正, 张卫国(2012)[13]以沪铝期货市场为研究对象, 针对金融市场的有偏性、尖峰厚尾性, 结合条件极值理论与SKST分布刻画金融市场的极端风险, 同时运用滚动时间窗口方法对不同波动率模型进行样本外动态VaR预测，并引进一种新的风险检验方法——MRC-SPA检验, 实证结果显示EVT有效提高了GARCH模型的样本外动态VaR预测精度, 其中GARCH-SKST-EVT -POT模型以较小的市场风险资本实现风险规避, 预测效果最优。

虽然以往研究已较为丰富和深入，但仍存在不足。和以往研究相比较，本文的研究特点在于：(l)采用上海期货交易所铜、铝期货价格指数日内高频数据（每10分钟）为研究样本；(2)构造了在期货市场较少运用到的经调整的已实现极差波动率估计序列；(3)运用6种损失函数来比较GARCH族模型波动率预测精度的优劣；(4) 采用了一种渐进正态分布检定法评估6类GARCH族模型的预测效果。

1 数据说明与描述分析

1.1数据说明

长期以来，由于受到各种条件限制，对金融时间序列的研究大都是针对低频数据（以日、周、月等为抽样频率）进行的。随着信息技术快速发展，数据采集难度及成本已大大降低，对高频金融数据（以小时、分钟、秒为抽样频率）的研究成为可能，高频率数据已逐渐成为研究金融市场资产价格波动的重点。为了更好反映沪铜、沪铝期货市场信息，本文采用上海期货交易所铜、铝期货价格指数的高频数据作为研究样本，抽样频率为10分钟。样本区间为2011年12月7日到2013年9月30日，剔除掉节假日以及异常信息交易点，共计438个交易日。每个交易日可记录的10分钟高频交易数据为25个，总体样本合计10950个，记为。

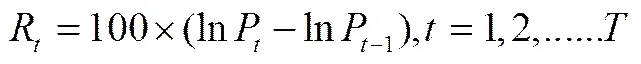
（2）

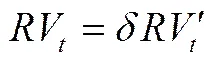
虽然，已实现波动是积分波动的一致估计[17]。但遗憾的是, 已实现波动率的一致性却因为抽样频率的限制以及市场微噪声干扰等因素影响而不能实现。为了更加精确的度量波动率，在极差理论的基础上，Christensen等人给出了新的估计量（已实现极差）[18]。首先将每日间隔标准化为1，将第天划分为个长度为的时间段，其中。在的时间段内，定义最后一个价格为，最高价格为，最低价格为，令，已实现极差则定义为日内对数价格的平方和：

（4）

研究表明，当证券价格服从几何布朗运动时,已实现极差波动也是积分波动的一致估计[19], 由于已实现波动的方差达到已实现极差方差的5倍，因此在理论上已实现极差比已实现波动至少高效5倍。Hansen和Lunde研究指出[20]，由于金融市场不能够连续24小时交易, 因此在无交易时段，采集的高频数据无法较好反映市场真实波动情况。因此, 需要对已实现极差进行调整。根据Marten等人的建议[21]，可以对已实现极差进行调整，经调整的已实现极差定义为：

1.2 数据描述分析

图1分别给出了沪铜、沪铝期货价格指数、日收益率以及已实现极差序列的波动情况。在全球金融危机的冲击下，由于国际大宗商品价格大幅波动以及内部需求的放缓，对沪铜、沪铝期货价格造成了巨大的冲击，导致价格波动幅度较大，相对于沪铜而言，沪铝期货价格出现了一定程度单边下跌的态势。两类期货日收益率以及已实现极差序列存在波动聚集性效应。表1给出了两类期货已实现极差序列的统计特征结果。

从表1结果可以看出，两类期货已实现极差序列偏度均为正，呈右偏分布；峰度值远远大于正态分布峰度值3，并且峰度系数和J-B统计量均在1%的水平下显著，表明两类期货已实现极差序列不是正态分布，表现出明显的“尖峰厚尾”的特点，且沪铜比沪铝的特征更明显；滞后阶数为20阶的Ljung-Box的Q统计量均在1%水平下显著，两类序列存在自相关性，说明波动存在长期记忆性或持续性特征；对残差进行滞后阶数为20阶的ARCH –LM检验，均在1%水平下显著，说明两类序列存在ARCH效应，具有条件异方差波动性；从phillips-perron检验以及ADF单位根检验看出，在1%水平下，两类序列显著拒绝了存在单位根的原假设，表明两类序列都是平稳的时间序列，从而可以进一步利用异方差模型进行金融计量分析。

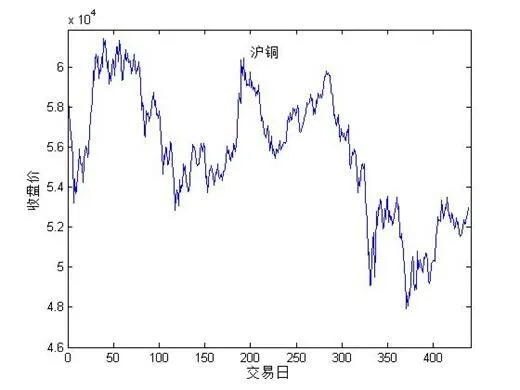
图1沪铜、沪铝期货价格指数、日收益率、已实现极差序列波动图

表1已实现极差序列的统计特征

均值标准差偏度峰度J-B统计量Q (20)ADF值P-PARCH(20) 沪铜沪铝0.02190.01120.03430.2124.848***3.747***16.634 ***11.360***1644.141 ***1481.707***32.381***26.391***-2.868***-2.671***-20.154***-13.688***303.965***289.021 ***

说明：***代表在1%水平上显著，Q(20)表示滞后阶数为的Ljung-Box Q统计量，ADF和P-P表示Augmented Dickey-Fuller单位根检验以及Phillips-Perron单位根检验结果。

2 GARCH族模型描述

在金融市场，描述市场波动特征较多的模型是Engle的自回归条件异方差模型（ARCH）、Bollerslev的广义自回归条件异方差模型（GARCH）[22-23], 随后在此基础上又发展出了其他非线性的GARCH族模型。下面是本文所要考察的6类GARCH族模型：

IGARCH()模型：

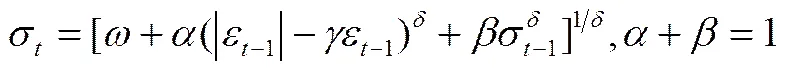
在金融市场中,研究者们发现，市场价格下跌所造成的市场波动比价格上涨更大,为了更好描述这种非对称冲击，Nelson（1991）提出了指数GARCH模型，即EGARCH模型。

EGARCH() 模型：

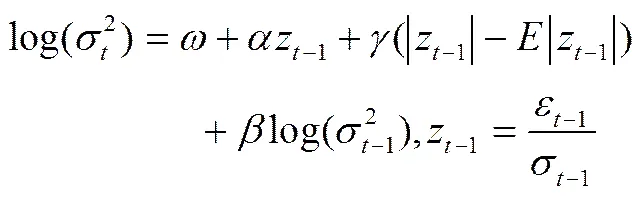
GJR() 模型：

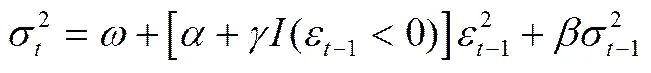
(.)为指示函数，当( )中条件成立时，取值为1，否则取值为0。如果，表明前一期的负收益率将导致本期有更高的收益波动。

Ding，Granger 和Engle(1992) 提出了一类不对称幂ARCH模型，及APARCH模型。

APARCH()：

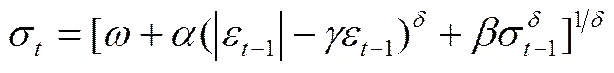
在GARCH模型的基础上, 为了模拟波动率的长记忆性以及自相关性, Baillie, Boller-slev和Mikkelsen(1996) (简记为BBM)引入了FGARCH -BBM模型。

FIGARCH()模型：

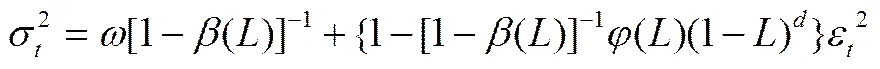
Davidson(2001)提出了广义FIGARCH模型，称为Hyperbolic GARCH模型。在HYGARCH模型中，参数d可以用来度量模型的双曲线记忆。

HYGARCH() 模型：

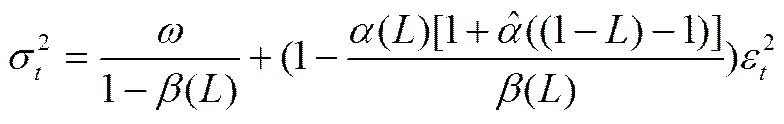
3 模型预测能力检验方法说明

3.1模型预测精度比较方法说明

本节利用上述6类GARCH族模型对两类期货的样本数据做样本外估计。将438个数据样本划分为两部分：“观测样本”和“预测样本”。其中，前300个（）数据为观测样本，而最后138个数据（）为预测样本。然后在保持观测样本长度不变的情况下，采用递推方式，以1作为递推周期连续向后递推，每递推1次，就重新估计模型参数，从而可以得到未来1天的波动率预测值。即对上述6类GARCH族模型，都分别重复进行了138次模型估计，这样每个模型就可以得到138个未来1天的样本外波动率估计值，记为，。同理，在预测样本区间内，记已实现极差估计为，并把它作为市场波动率的参考标准，用来比较6类GARCH模型的预测精度。

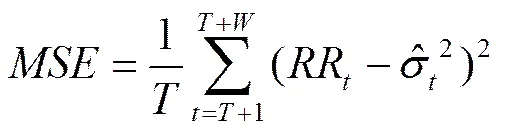
（12）

，

，

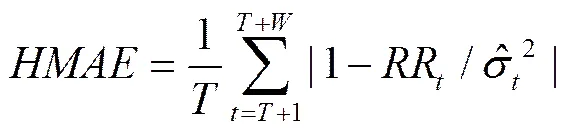
（14）

3.2 Diebold-Mariano检验方法说明

虽然采用损失函数作为比较标准,可以对比模型的预测精度，并以此判断不同模型的优劣,但无法检验比较结果在统计上是否具有显著性。为解决这一问题，Diebold和Mariano提出了一种渐进正态分布检验法（简称DM）。DM检验法不要求损失函数的形式及误差的限制，使这个检验方法具有相当强的检验力，因此受到广泛的应用。其实现过程简介如下：

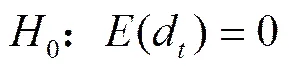
（16）

其中：

（18）

4实证结果

4.1模型参数估计结果

表2给出了6类GARCH族模型假设下的沪铜和沪铝期货的参数估计结果。表中每一个参数都对应了两行参数估计结果,其中第一行代表的是沪铜期货的参数估计结果,第二行代表的是沪铝期货的参数估计结果。

由表2结果获知：（1）IGARCH模型假设下的沪铜、沪铝参数估计结果+之和为1，满足IGARCH模型的约束条件；（2）IGARCH、EGARCH、GJR和APARCH模型参数均大于0，表明两类期货序列波动呈现出集聚性，由于国内期货投资者对国家出台的相关政策过于敏感，所以造成在利空或利好消息的刺激下，产生期货价格过度下跌或上涨的现象，体现了期货价格波动的集聚性；（3）六个模型参数+之和都接近于1,表明两类期货序列波动剧烈且具有较大的持续性,波动率的衰减较缓慢，风险较大。铜、铝作为一种国际大宗商品，价格很容易受到国内外多种因素的影响，比如国内外宏观经济政策的变化、国际期货交易价格的变化、美元对人民币汇率的变化等，特别需要注意的是，这些因素的变化往往也具有一定的持续性；（4）EGARCH、GJR和APARCH模型参数均小于0，且杠杆系数均在5％的水平下显著，表明沪铜、沪铝期货市场存在杠杆效应。和国外成熟市场相比较，我国期货市场发展还存在许多不完善的地方，投资者在期货市场进行投资的时候，其投资行为容易受到国内外各种消息的影响，投资者更加关注的往往不是“好消息”对市场的冲击，而是“坏消息”对市场的冲击，“坏消息”所引起的市场波动比“好消息”所引起的市场波动幅度还要大；（5）模型参数显著，表明沪铜、沪铝期货市场的预期收益会受到风险水平的影响；（6）FIGARCH和HYGARCH模型参数均满足的条件，表明沪铜、沪铝期货市场波动存在长记忆性，而且沪铝的长记忆参数均大于沪铜的长记忆参数，说明在长记忆性方面，沪铝期货市场强于沪铜期货市场。

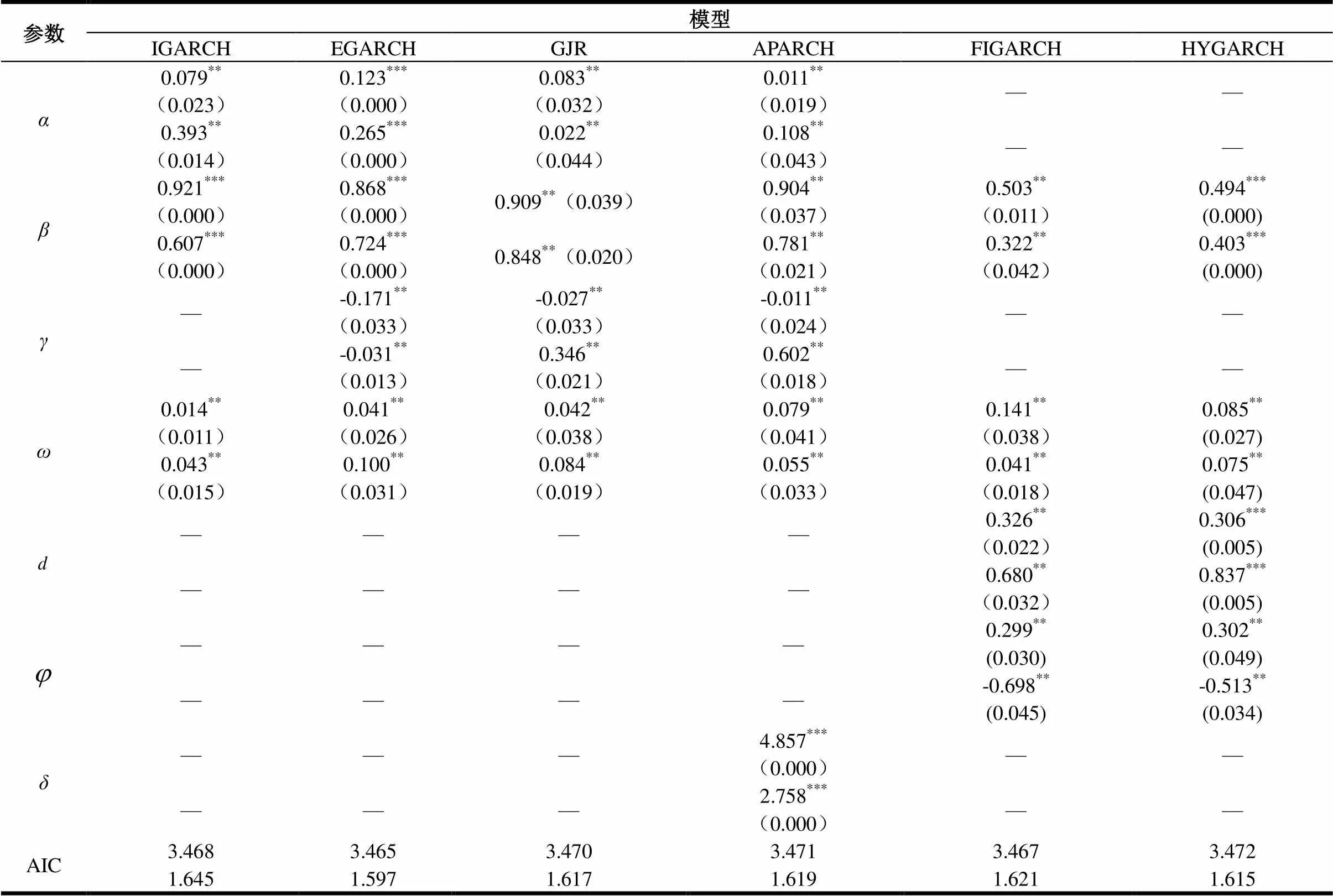
表2 模型参数估计结果

说明：**和***分别代表在5％以及1％水平上显著，数字下方的圆括号中是对应检验的值， AIC 是平均赤池信息。

采用最小赤池准则(AIC)进行模型拟和优劣判别,对于沪铜期货市场而言，EGARCH模型拟合效果最好, FIGARCH模型次之；对于沪铝期货市场，同样，，EGARCH模型拟合效果最好, HYGARCH模型次之。总体来说，各模型之间差距并不大，定量的判断结果还需要通过下面各类损失函数值的计算。

4.2 波动率模型预测精度及DM检验结果

表3和表4给出了基于6类损失函数的GARCH族模型预测精度及DM检验结果。

表3模型预测精度比较及DM检验结果

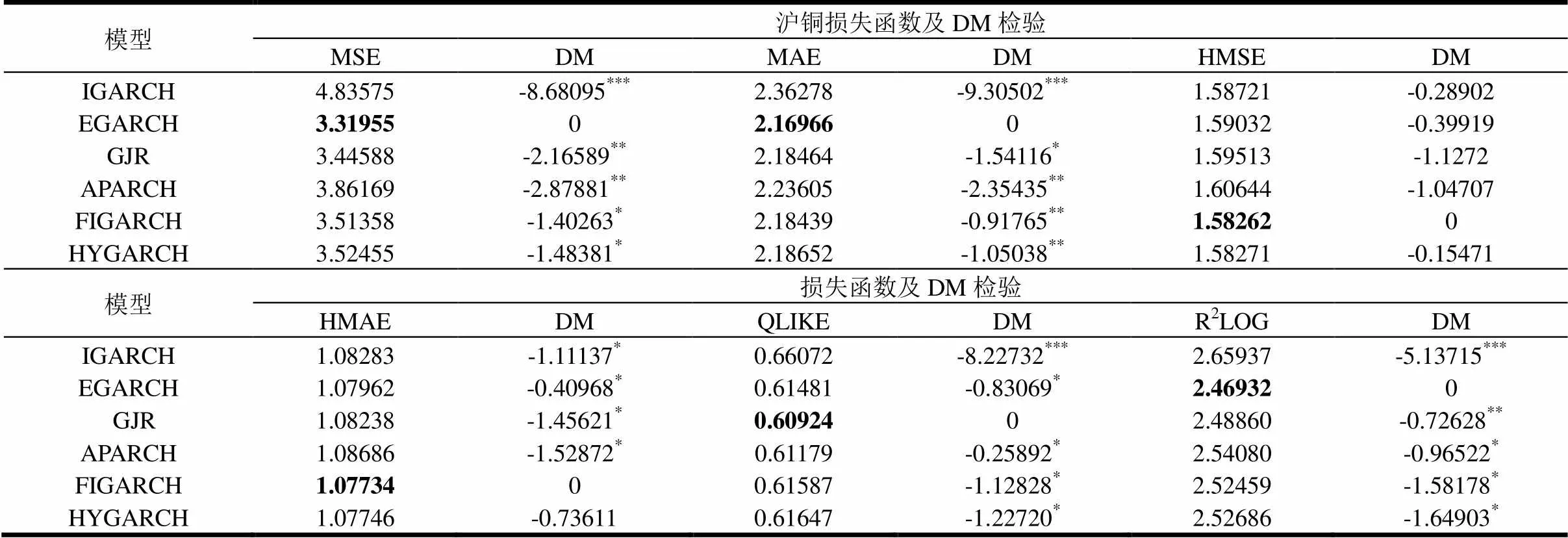
模型沪铜损失函数及DM检验 MSEDMMAEDMHMSEDM IGARCH EGARCH GJR APARCHFIGARCHHYGARCH4.835753.319553.445883.861693.513583.52455-8.68095***0-2.16589**-2.87881**-1.40263*-1.48381*2.362782.169662.184642.236052.184392.18652-9.30502***0-1.54116*-2.35435**-0.91765**-1.05038**1.587211.590321.595131.606441.582621.58271-0.28902-0.39919-1.1272-1.047070-0.15471 模型损失函数及DM检验 HMAEDMQLIKEDMR2LOGDM IGARCHEGARCH GJR APARCHFIGARCHHYGARCH1.082831.079621.082381.086861.077341.07746-1.11137*-0.40968*-1.45621*-1.52872*0-0.736110.660720.614810.609240.611790.615870.61647-8.22732***-0.83069*0-0.25892*-1.12828*-1.22720*2.659372.469322.488602.540802.524592.52686-5.13715***0-0.72628**-0.96522*-1.58178*-1.64903*

说明：表中*、**以及***分别代表DM检验统计量在10％、5％以及1％水平上显著，黑体数字表示在不同损失函数标准下的最小损失值。

表3结果显示：（1）在MSE、MAE、R2LOG这3种损失函数标准下，EGARCH模型具有最小损失函数值，获得了最高的波动率预测精度；（2）在HMSE和HMAE损失函数标准下，FIGARCH模型获得最高的波动率预测精度；（3）在QLIKE损失函数标准下，GJR模型获得最高的波动率预测精度。

由上可知，在不同损失函数标准下，EGARCH、FIGARCH以及GJR模型具有最高的波动率预测精度，但总体来说，EGARCH模型预测精度相对最好。为了更好评估模型的预测能力，这里利用EGARCH、FIGARCH以及GJR模型在各自对应的损失函数标准下分别和其它模型进行DM检验，检验结果表明：（1）在MSE、MAE、R2LOG以及QLIKE损失函数标准下，所有检验结果拒绝零假设，说明EGARCH和GJR模型的预测能力和各自对应的其他模型相比较，具有显著差异；（2）在HMSE损失函数标准下，所有检验结果没有拒绝零假设，说明FIGARCH模型的预测能力和其他模型相比较，不具有显著差异；而在HMAE损失函数标准下，FIGARCH模型和HYGARCH模型的检验结果表明其预测能力不具有显著差异。

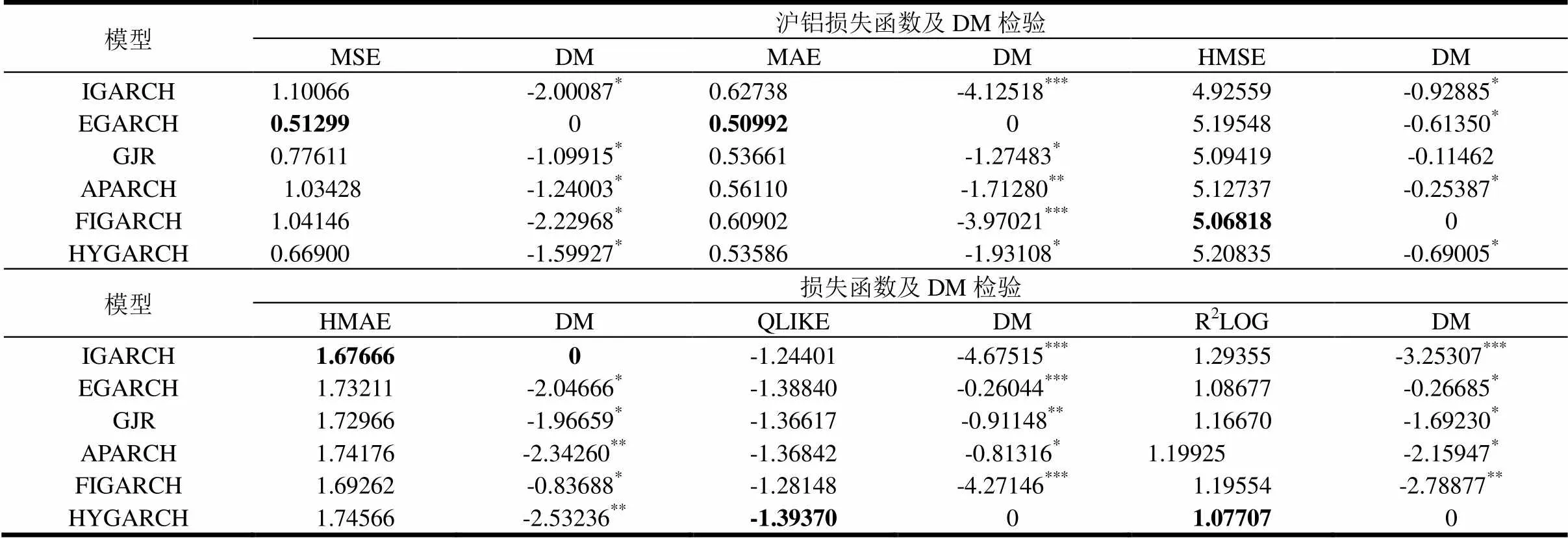
表4 模型预测精度比较及DM检验结果

说明：表中表中*、**以及***分别代表DM检验统计量在10％、5％以及1％水平上显著，黑体数字表示在不同损失函数标准下的最小损失值。

表4结果显示：（1）在MSE、MAE损失函数标准下，EGARCH获得最高的波动率预测精度；（2）在HMSE损失函数标准下，FIGARCH模型获得最高的波动率预测精度；（3）在HMAE损失函数标准下，IGARCH模型获得最高的波动率预测精度。（4）在QLIKE、R2LOG损失函数标准下，HYGARCH模型获得最高的波动率预测精度。总体来说，，EGARCH模型和HYGARCH模型预测精度相对最好。

和沪铜期货相类似，这里利用EGARCH、FIGARCH、IGARCH以及HYGARCH模型在各自对应的损失函数标准下分别和其它模型进行DM检验，检验结果表明：（1）在MSE、MAE、HMAE 、QLIKE 以及R2LOG损失函数标准下，所有检验结果拒绝零假设，说明EGARCH、IGARCH、HYGARCH模型预测能力和各自对应的其他模型具有显著差异；（2）在HMSE损失函数标准下，FIGARCH模型和GJR模型的检验结果表明其预测能力不具有显著差异。

5 结论

中国自1990年创办期货市场以来，在期货市场研究中，对期货价格波动特征的研究一直是一项基础性工作，且具有非常重要的意义。只有充分认识到期货价格的波动特征，管理层才能加强期货市场的风险控制和管理。基于此，文章选取上海期货交易所铜、铝期货价格指数日内10分钟高频收益数据，构造了经调整的已实现极差波动率估计序列，针对6类GARCH族模型样本外波动率预测能力的比较进行了实证分析。实证结果显示，沪铜、沪铝期货市场上已实现极差波动率估计序列具有尖峰厚尾、集聚性、持续性等特征。对于沪铜期货市场，EGARCH模型具有相对较好的的波动率预测能力，在某些损失函数标准下，FIGARCH以及GJR模型也体现出了较好的波动率预测能力，但FIGARCH模型的预测能力和其它模型相比较并不显著；对于沪铝期货市场，EGARCH和HYGARCH模型具有相对较好的的波动率预测能力，而在某些损失函数标准下，FIGARCH以及IGARCH模型也体现出了较好的波动率预测能力。文章的研究方法和实证结果，对于填补针对期货市场，以极差波动作为基准波动进行实证研究的空白，更好的解释期货市场价格波动的特征，直接丰富GARCH族模型在中国期货市场的应用具有重要的现实意义。同时也希望管理层加强中国期货市场的监督管理与建设，管理层可以充分考虑放宽期货市场准入条件，鼓励多类型机构投资者进入期货市场，时加强对投资者的教育，遏制期货市较强烈的投机气氛。

[1] 郑丰,崔积钰,马志伟. 沪铜期货市场波动聚集现象研究[J]. 技术经济与管理研究, 2013,5(9): 76-80.

[2] 朱学红, 沈玉芳, 邵留国. 石油和汇率冲击下的中国金属价格波动行为[J]. 系统工程, 2012,30(11): 30-35.

[3] 武琳,丁浩. 铜期货市场波动对国内现货价格影响的实证研究[J]. 价格理论与实践, 2012,10(3): 53-55.

[4] 程慧,黄健柏,郭尧琦. 我国有色金属价格波动周期性研究[J]. 价格理论与实践, 2012,30(9): 50-51.

[5] 崔海蓉,何建敏,张京波. 我国有色金属期货波动溢出效应研究[J]. 北京理工大学学报（社会科学版）, 2011,13(4): 29-32.

[6] 李丹宁,穆铮.基于非参数估计方法的沪铜期货价格研究[J]. 经济数学, 2012,29(3): 17-21.

[7] 张保银,陈俊.基于动态VECM 的我国铜期货的价格发现功能研究[J]. 天津大学学报（社会科学版）, 2012,14(6): 492-496.

[8] 胡龙,胡太军.基于VECM-GARCH 模型的沪铜指数与上证指数的联动分析[J] 金融与经济,2011,62(6): 62-70.

[9] 王泰强,侯光明. 基于VaR的中国有色金属期货市场风险测度研究[J].东北财经大学学报,2011,78(6):26-30.

[10] 李莎姗.沪铜期货市场收益率波动特征实证研究[J]. 企业研究,,2010,21(10):53-55.

[11] 方燕,庞小利.沪铜期货价格与现货价格波动关系的实证分析[J]. 价格理论与实践,2010,26(8):60-61.

[12] 赵伟雄，崔海蓉，何建敏.GARCH 类模型波动率预测效果评价——以沪铜期货为例[J].西安电子科技大学学报（社会科学版）,2010,20(4):27-32.

[13] 方伟正, 张卫国. 有偏分布下的动态风险测度及MRC-SPA 检验[J]. 系统工程,2012,30(7):8-13.

[14] Andersen T G, Bollerslev T, Meddahi N. Correcting the errors: volatility forecast evaluation using high frequency data and realized volatilities[J]. Econometrica, 2005, 73: 279-296.

[15] Andersen T G, Bollerslev T. Answering the skeptics: yes, standard volatility models do provide accurate forecasts [J]. International Economic Review, 1998, 39: 885-905.

[16] Hansen P R, Lunde A. Consistent ranking of volatilitymodels[ J ]. Journal of Econometrics, 2006, 131: 97 -121.

[17] 于亦文.实际波动率与GARCH 模型的特征比较分析[J].管理工程学报,2006,20(2):65-69.

[18] Christensen K, Po do lski M. Asym pto tict heory forrange-based est imation o f integ r ated var iance o f acontinuous semi-mar ting ale [ Z] . Aar hus Schoo l ofBusiness, 2005.

[19] 唐勇, 张世英. 高频数据的加权已实现极差波动及其实证分析[J]. 系统工程,2006,24(8):52-57.

[20] H ansen P R, Lunde A. A forecast comparison of volatility models: does anyth ing beat a GARCH ( 1, 1) [ J].Journa l o fApplied E conometrics, 2005, ( 20): 873-889.

[21] M artensM, D ijk D. M easuring volatility with the realized range[ J]. Journal o f Econom etrics, 2007, ( 138): 181-207

[22] Bonanno ,G1 ,F1Lillo ,R1N1Mantegna. Levels of complexi2ty in financial markets[J ]1Physica A , 2001 ,299 :16-27

[23] Mantegna,Stanley. An Introduction to Econo2physics :Correlations and Complexity in Finance[M] . Cam2bridge University Press ,Cambridge , 2001 ,199 :43-52

Comparative Study on Prediction Model of High-frequency Fluctuation of China's Futures Market

CHEN Xiao-dongn

(School of Mathematics and Finance ,School of Chongqing University of Arts and Science, Chongqing 402160, China)

The financial asset volatility has always been the focus in the field of financial economics. Selecting the appropriate volatility model of asset prices fluctuation to accurately estimate and forecast as accurately as possible has theoretical and practical significance in the fields of pricing model, portfolio allocation, risk measurement and risk management. China's financial market develops at rapid speed but in low maturity. The market often fluctuates drastically. In Chinese financial market, the realized range based volatility as a more accurate and effective estimation of volatility is noticeably absent from the empirical study on the futures market.Based on this, the present study selects high frequency data for 10 minutes of copper futures and aluminum futures price index in the Shanghai Futures Exchange. It structures the realized range based volatility for the measurement and comparison of GARCH group model’s prediction accuracy. It has important practical significance for better explanation of futures volatility and the application of GARCH models in Chinese futures market.The first part of this paper introduces the data sample and range volatility estimation method. The second part introduces the construction of GARCH family model. The third part describes the sample volatility forecasting method and DM test. The fourth part provides empirical analysis results, followed by the conclusion in the fifth section.The empirical results show that the realized range based volatility of copper, and aluminum futures market has the characteristics of fat-tail distribution, clustering and persistence. For the copper futures market, the EGARCH model has a better volatility forecasting ability. The FIGARCH model and GJR model also reflect the good volatility forecasting ability in terms of some loss function standards. For Shanghai aluminum futures market, the EGARCH model and HYGARCH model have a better volatility forecasting ability. The FIGARCH model and IGARCH model also reflect the good volatility forecasting ability in terms of some loss function standards.The test method and the empirical results of this paper have important reference values for Chinese futures market participants’ designing hedging strategy, which can help manage and control the market risk in Chinese futures markets. We suggest that the management should promote the development of domestic futures broker firms, open channels of business, and ease the limitation of business scope in the premise of enhancing administrative supervision. It is also important to establish modern financial service enterprise systems in compliance with international rules. In addition, these systems can help establish international rules of modern financial service enterprise systems, improve the management level of futures companies, provide professional consultation for Chinese enterprises to participate in international competition, and cultivate professional risk management talents for the society. Consequently, Chinese companies can perform better when facing the challenges of integrating with international financial environment.

metal futures; volatility;garch model; DM test

中文编辑：杜 健；英文编辑：Charlie C. Chen

F224

A

1004-6062(2016)03-0114-07

10.13587/j.cnki.jieem.2016.03.014

2013-10-15

2014-03-23

国家自然科学基金资助项目（71271227）, 重庆市高校创新团队建设计划资助项目（KJTD201321）

陈晓东（1977－），男，汉，重庆人；副教授，研究方向：金融工程、经济数学。