轨道交通SBOT项目特许期的合作博弈模型研究

吕俊娜，刘 伟，邹 庆，甘 琳



轨道交通SBOT项目特许期的合作博弈模型研究

吕俊娜1,2，刘 伟1，邹 庆1，甘 琳3

（1.重庆大学经济与工商管理学院，重庆，400030；2.重庆交通大学管理学院，重庆，400074；3.重庆大学建设管理与房地产学院，重庆，400045）

轨道交通SBOT模式是一种新的BOT衍生模式。特许期作为SBOT项目特许权协议的关键决策参数之一，对于轨道交通项目运作的成功与否至关重要。考虑到轨道交通SBOT项目的不确定性特征，在综合评估项目经济和社会效益的基础上，利用实物期权理论中经典的不可逆投资模型，构建了不确定条件下SBOT项目的特许期决策模型，其决策程序分为两步：首先，根据不可逆投资理论分别构建了项目各投资主体的最优投资时机决策模型，得到特许期的可行区间；为进一步讨论特许期的均衡解，根据合作博弈理论，利用公共部门/私营部门的扩展NPV函数，构建了以合作双方整体利益最大化为决策目标的特许期计算模型，求解出特许期的合作均衡解，并分析了均衡解的性质，最后通过算例对轨道交通SBOT项目特许期的合作博弈模型进行了验证。

SBOT项目；特许期；实物期权；扩展NPV

0 引言

轨道交通作为解决城市交通拥挤与排放问题的有效途径，成为我国城市基础设施建设和投资的重点领域。由于轨道交通项目投资规模大，传统的以政府公共资金为主导的投融资模式已不能完全满足我国城市基础设施建设发展的需要。利用社会资本进入基础设施领域最常用的方式是BOT模式，然而由于轨道交通项目造价高、运营成本高等特点，票款收入难以保障项目正常运作或不足以使得社会投资者获得合理回报，因此，政府采用BOT模式运作轨道交通项目时需要对其进行补偿。目前，在项目实践中，通常采用资本补偿即SBOT (Subsidize in Building，Operate and Transfer) 模式来运作轨道交通项目，SBOT是指公共部门通过对轨道交通项目进行资本补偿性投入来满足私营部门的盈利要求[1]。北京地铁4号线，杭州地铁1号线，北京地铁14号线等均采用SBOT模式建设。特许期作为SBOT项目特许权协议的关键决策参数之一对于轨道交通项目运作的成功与否至关重要。轨道交通SBOT项目特许期过短，私营部门将会制定较高的收费机制从而把部分风险转移给乘客，进而损害公众利益；而在项目经济寿命期一定的情况下，特许期过长会减少特许期期满后项目的运营期，进而损害公共部门的利益[2]。轨道交通项目投资一般具有投资成本部分或完全不可逆、预期收入的不确定性以及投资时机的可延迟性等特征[3-4]，忽视项目延迟期权的价值，会造成项目价值被低估，进而导致特许期过长[5]。因此，研究不确定条件下轨道交通SBOT项目的特许期决策模型具有重要的理论和实践意义。

现有文献对于资本补偿下轨道交通SBOT模式的研究尚处于初步探索阶段[6-8]，对SBOT项目特许期决策模型研究的报道，至今尚未见到。而有关特许期决策模型定量研究的文献主要集中在传统的BOT项目且主要是采用NPV (Net Present Value) 方法，依据项目预测现金流对BOT项目的特许期可行域进行计算，如Shen等[9]构建了公共部门/私营部门决策BOT项目特许期的基准条件。通过文献[9]，可方便计算出特许期的可行域，但文献[9]在对经济变量进行估计时并未考虑到风险及不确定性因素对其的影响，Shen和Wu[10]在文献[9]的基础上，借助蒙特卡洛模拟 (Monte Carlo) 技术，构建了考虑风险的BOT项目特许期决策模型。Wu等[11]认为项目移交给公共部门时的净残值是公共部门收入的一部分，修正了文献[9]中的政府决策边界条件。考虑到交通BOT项目的不确定性特征和NPV方法的局限性，刘伟等[12]利用实物期权理论，构建了不确定收益下高速公路BOT项目的特许期决策模型。但文献[12]在BOT项目特许期决策模型的构建中仅考虑了项目的财务可行性，而轨道交通项目作为一种低能耗、低污染的绿色交通方式，可减少交通拥挤、环境污染和交通事故，具有显著的社会效应，公共部门应该对其进行补偿，因此，在轨道交通SBOT项目的特许期决策模型研究中应该同时考虑项目的经济和社会效应[11]。基于此，考虑到轨道交通项目的社会效应特征，本文根据经典的不可逆投资理论构建了政府资本补偿下轨道交通SBOT项目特许期决策模型。

为了进一步缩小特许期的可行域，借助博弈论方法，可以得到BOT项目特许期的均衡解。BOT项目特许期决策过程可以看作是公共部门与私营部门之间的完全信息动态博弈问题[13-14]，如Shen等[15]根据讨价还价理论，在文献[9]的基础上，建立了特许期的博弈模型，缩小了特许期的可行域，但在文献[15]中，假定总投资成本不变，而项目实践中，不同的特许期可能会使总投资成本发生变化，鲍海君[16]从私营部门的角度，建立了总成本可变下特许期的博弈模型。Hanaoka和Palapus[17]在文献[10]和[15]的基础上，以菲律宾的交通BOT项目为研究对象，利用Monte Carlo模拟与博弈论相结合的方法构建了特许期的决策模型并对其进行了案例研究。刘伟等[12]构建了高速公路BOT项目特许期的Stackelberg博弈模型并求解出模型的均衡解。但文献[12]假定政府具备完全的讨价还价能力，而在轨道交通项目实践中，参与SBOT项目运营的社会投资者往往具有一定的技术优势，因此，Stackelberg博弈分析并不完全适合轨道交通SBOT项目的特许期决策模型研究，而且在Stackelberg博弈分析中，博弈主体追求的是自身利益最大化，而非系统整体利益最大化，会导致社会福利损失。基于此，本文提出在公共部门/私营部门合作情况下，以系统整体利益最大化为决策目标来构建轨道交通SBOT项目特许期的合作博弈决策模型。

综上所述，考虑到轨道交通SBOT项目的不确定性特征，在综合评估项目经济和社会效益的基础上，利用实物期权经典的不可逆投资理论，建立了公共部门/私营部门投资SBOT项目的投资决策模型，并求解出特许期的可行域；在此基础上，根据合作博弈理论，利用公共部门/私营部门的扩展NPV (Extended net present value) 函数，构建了以合作双方整体利益最大化为决策目标的特许期计算模型，求解出特许期的均衡解。研究结论为轨道交通SBOT项目特许权协议双方决策特许期的提供了一种新思路。

1 模型

1.1 问题描述

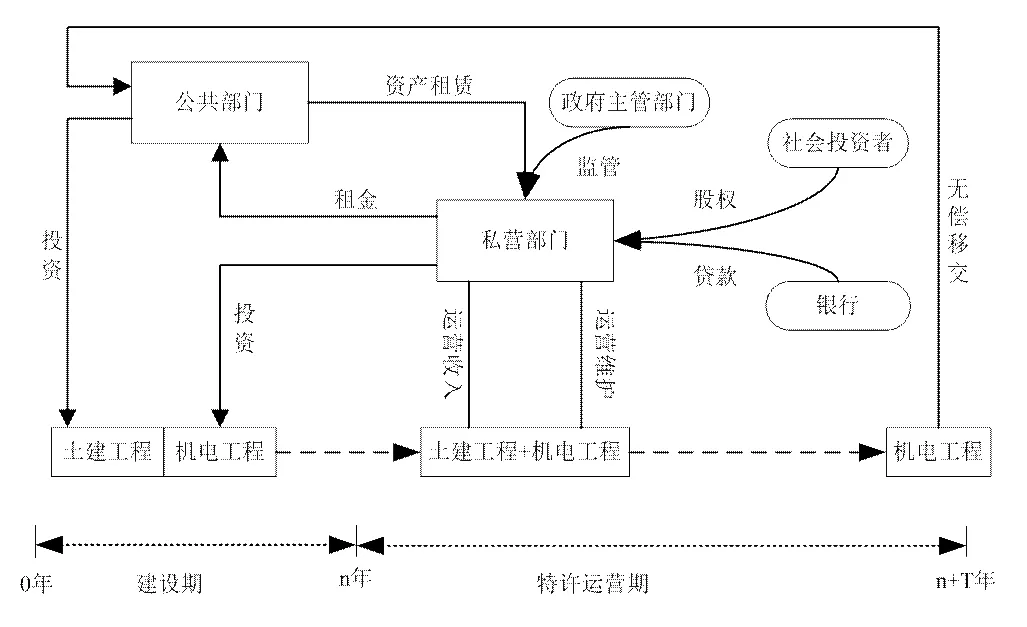
图1 城市轨道交通SBOT项目运作模式

假设某城市轨道交通项目拟采用SBOT模式融资建设，项目总投资为，其中公共部门投资为，主要负责土建工程部分的投资和建设；私营部门投资为，主要负责项目机电设备的投资和建设，。特许期内，私营部门负责轨道交通项目的运营和维护，并通过运营收入来回收投资，同时通过向公共部门缴纳租金来获得项目土建工程部分的使用权；租金用来表示，不仅可以回收公共部门的投资成本，而且可以防止私营部门通过垄断地位而获得超额收益。轨道交通项目运营收入包括票款收入、广告以及站内商业收入，其中票款收入是轨道交通项目最主要的收入来源，占运营收入的比重为。具体如图1所示。

1.2 基本假设

本文在建模之前，首先提出以下基本假设：

假设1：轨道交通SBOT项目的投资成本是部分或完全不可逆投资，且在项目建设初期（即“0”期）一次性投入。

假设2：轨道交通项目客流量的增长因受到居民出行方式、公共交通服务水平以及经济发展情况稳定性因素的影响，同时也受到大型活动举办等随机因素的影响，故假定轨道交通SBOT项目客流量服从几何布朗运动(GBM)[3]:，其中为常数，表示客流量的预期增长率，也为常数，表示客流量的波动程度，为维纳过程的增量，服从正态分布，其中，。

假设3：轨道交通项目可缓解交通拥挤，具有减少空气和噪音污染，降低能源消耗和交通事故等的社会效益[18-20]，用来表示，根据“谁受益，谁补偿”原则，本文的社会效益主要是指与非轨道交通相比，轨道交通在空气污染、噪音污染和交通事故方面所具有正的外部效益[20]，[3,18]，其中表示与非轨道交通相比，轨道交通项目减少的社会成本，表示第年的客流量，表示运输距离。

1.3 SBOT项目特许期的可行域分析

1.3.1 公共部门能接受的最大特许期

假定政府拟采用SBOT模式吸引私营部门参与某轨道交通项目的建设和运营，双方约定：公共部门负责项目土建工程部分的投资和建设，而项目的车辆、信号、自动售检票系统等机电设备部分则交由私营部门投资和建设，特许期内私营部门通过资产租赁形式获得项目土建工程部分的使用权，并通过运营整个项目来回收投资成本，特许期期满，私营部门将项目的机电工程部分无偿移交给公共部门，特许期期满后，公共部门负责整个项目的运营，并通过运营收益来保障整个项目的正常运作。根据实物期权经典的不可逆投资理论，项目投资主体可以获得一个在未来某一时刻以预先谈判价格投资项目价值波动的轨道交通SBOT项目的权利，其执行价格为投资主体的初始投资，如公共部门的执行价格为，这种投资机会被看作是美式看涨期权，投资者做出何时投资的决策即确定何时执行这一权利从而使得项目价值最大，这是一个连续时间的最优停止问题，即存在某个投资临界值，当时，等待是最优的，当时，投资是最优的，相应的最优投资时机为首次达到的时刻，即[21]。在上述假设下，公共部门投资城市轨道交通SBOT项目的项目价值函数可以表述如下：

根据项目初始条件，价值匹配（value matching）和平滑粘贴（smooth pasting）条件:

(3)

可得出公共部门投资SBOT项目的投资临界值为

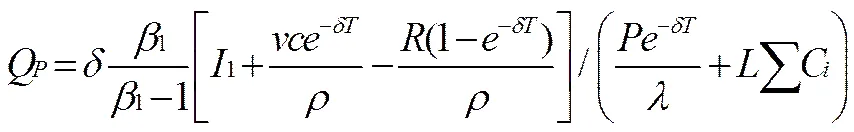
其中：(5)

(6)

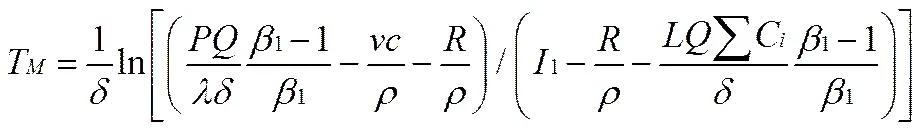
而

，

经推导，可得：

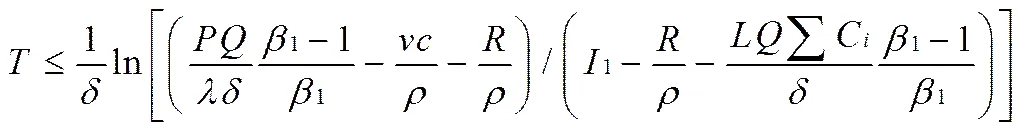
1.3.2 私营部门能接受的最小特许期

假定私营部门愿意投资轨道交通SBOT项目，则其须负责项目机电部分的投资，其投资额为，在特许期内，私营部门不仅负责SBOT项目的运营，同时还得负责整个项目(包括土建工程和机电工程部分)的运营维护，并向公共部门缴纳租金以获得项目土建工程部分的使用权，则私营部门投资城市轨道交通SBOT项目的项目价值函数可以表述为：

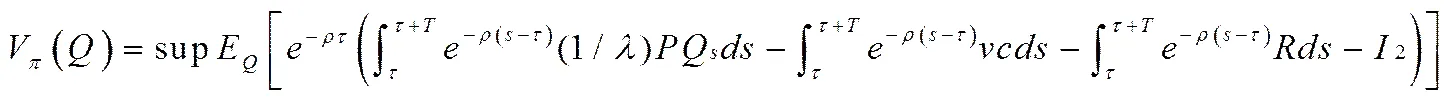
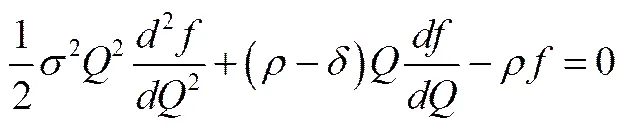
(10)

(12)

1.3.3 SBOT项目特许期的可行域

通过以上分析可知，为了使公共部门和私营部门在轨道交通SBOT项目投资上达成一致，其客流量须同时满足公共部门/私营部门的投资条件，由(7)式和(12)式，得

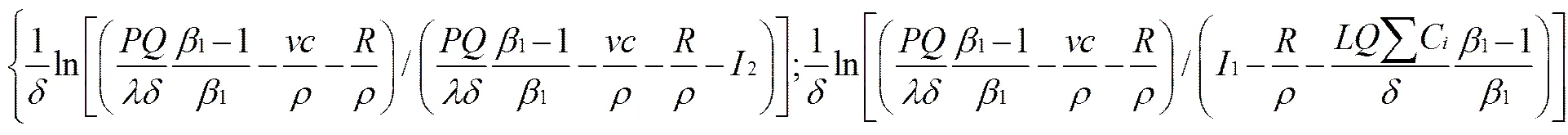
证明：显而易见，要使(13)式有意义，须满足

2 特许期的均衡解分析

为了进一步分析特许期的均衡解，首先以公共部门与私营部门各自的扩展NPV函数作为其投资决策的目标函数，这里扩展NPV等于项目预期净现值与期权价值之差[23]，分别以，表示公共部门、私营部门的扩展NPV函数。模型如下：

(15)

假定公共部门与私营部门在投资轨道交通SBOT项目的合作中，以系统的整体利益最大化为目标来决策项目的特许期，即有

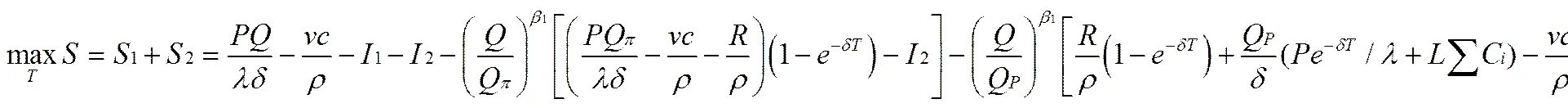
(17)

从(18)式可知，轨道交通SBOT项目特许期的合作均衡解与以下参数有关：公共部门的投资额，私营部门的投资额，特许价格，运营成本，贴现率，与非轨道交通相比，轨道交通项目减少的社会成本，运输距离等。在项目实践中，当公共部门与私营部门合作投资轨道交通SBOT项目时，利用项目基本参数，根据(18)式，可以方便地计算出SBOT项目特许期的合作均衡解。

3 均衡解的性质与讨论

证明：由（4）、(11)和（13）式，得

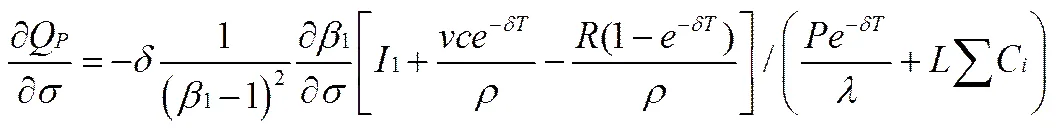
性质1表明了客流量的不确定性对轨道交通SBOT项目投资阈值的影响，即随着SBOT项目客流量波动率的增大，其投资阈值随之增大，使得项目投资主体的等待更有价值，项目投资主体更倾向于推迟投资。在项目实践中，投资主体在进行轨道交通SBOT项目投资决策时，由于面临各种风险如客流量风险、相关政策变动风险等，因此投资主体往往投入更多成本进行项目可行性论证，从而推迟投资。

证明：由（18）式，得

记

,

证明：由（18）式，得

证明：由（18）式，得

性质2-4分别表明了公共部门投资额、租金以及轨道交通项目社会效应系数对特许期合作均衡解的影响，即轨道交通SBOT项目特许期合作均衡解随着公共部门投资额的增大而减小，随着租金的增大而增大，随着社会效应系数的增加而增大。这和项目实践是吻合的，即根据“风险共担、利益共享”的原则，项目投资主体的利益分配要与其所承担的风险相匹配。

4 算例研究

以城市轨道交通SBOT项目为例，验证特许期决策模型的可行性以及均衡解的性质。国内某市计划采用SBOT模式吸引私营部门参与城市轨道交通项目建设，双方约定：项目土建部分由公共部门负责投资建设，其投资额为107亿元，项目设备部分由私营部门投资，其投资额为46亿元，根据项目收益测算，预计项目运营初期日客流量为98.63万人次，预期年均增长率为0.05，通过对相关项目历史数据的极大似然估计，得到运营收入的波动率为0.1。特许期内租金为0.42亿元，特许价格为3元，票款收入占运营收入的比重为0.7，项目年均运营成本为5.55亿元，项目的社会效益系数测定为2.37，项目的贴现率取0.1。

根据项目基本参数，得：

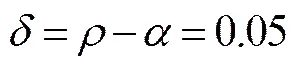
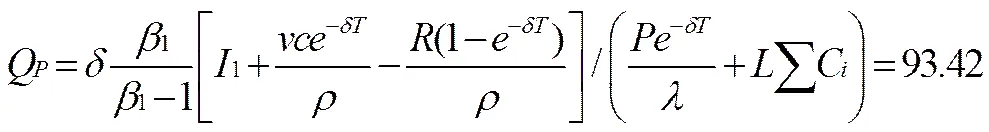
综合以上计算可知，公共部门与私营部门在预计项目运营初期日客流量为98.63万人次时进行SBOT项目投资是可行的，此时特许期的可行域为(17，24)，特许期的合作均衡解是为19；并且当特许期为19时，SBOT项目的投资临界值为93.97万人次/日。

为了进一步分析均衡解的性质，下面在其他参数固定情况下，分析不确定性对SBOT项目投资临界值的影响，以及公共部门的投资额、租金以及社会效应系数对特许期合作均衡解的影响，其中，，和的变动幅度为。

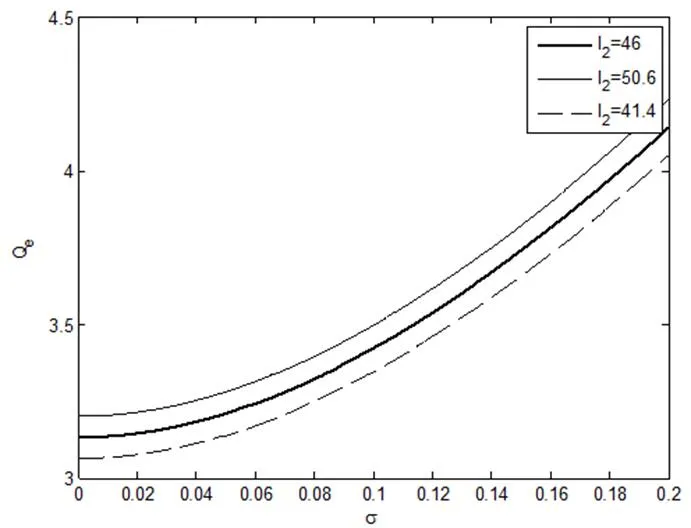
图2 不确定性对SBOT项目投资阈值的影响

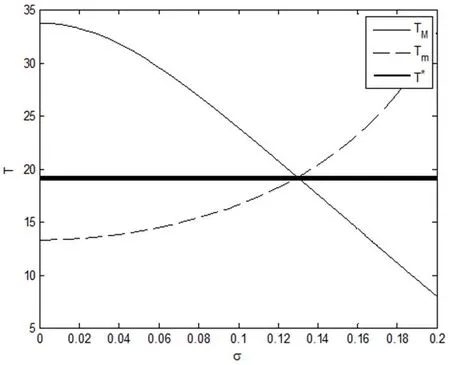
图3 不确定性对SBOT项目特许期的影响

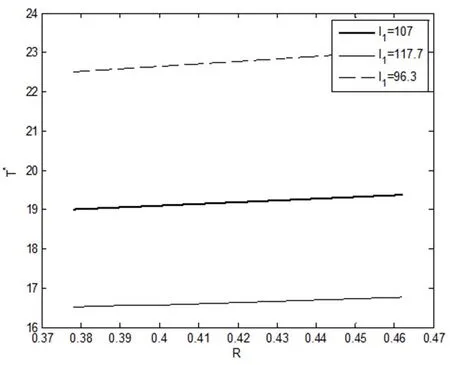
图4 租金对SBOT项目特许期均衡解的影响

图5 社会效应对SBOT项目特许期均衡解的影响

5 结束语

城市轨道交通作为解决交通拥挤与排放问题的最有效途径之一，具有显著的社会效益。考虑到轨道交通SBOT项目的不确定性等特征，在综合评估项目经济和社会效益的基础上，结合经典的不可逆投资模型与合作博弈理论，建立了轨道交通更SBOT项目特许期的合作博弈模型，根据“谁受益，谁补偿”原则，这里的社会效益主要是指与非轨道交通相比，轨道交通在空气污染、噪音污染和交通事故方面所具有正的外部效应这里的社会效益。假定客流量服从几何布朗运动，首先根据不可逆投资理论，建立了公共部门/私营部门投资轨道交通SBOT项目的决策模型，并求解出特许期的可行域；在此基础上，根据公共部门/私营部门的扩展NPV函数，构建了以合作双方整体利益最大化为决策目标的特许期决策模型，求解出特许期的合作均衡解。最后结合一个算例验证了轨道交通SBOT项目特许期的合作博弈模型的可行性和均衡解的性质，为公共部门/私营部门计算轨道交通SBOT项目特许期的合作均衡解提供了一种新思路。研究表明，随着客流量不确定性增大，轨道交通SBOT项目的投资临界值也随着增大，项目投资主体倾向于推迟投资；轨道交通SBOT项目特许期的合作均衡解随着公共部门投资额的增大而减小；随着租金的增大而增大；随着社会效益系数的增大而增大。

[1] 蔡蔚.我国城市轨道交通投融资体制演进机理探析[D].上海:同济大学,2007.

[2] Khanzadi M, Nasirzadeh F, Alipour M. Integrating system dynamics and fuzzy logic modeling to determine concession period in BOT projects [J]. Automation in Construction 2012, 22: 368-376.

[3] 高咏玲,杨浩,孙强.城市轨道交通项目建设时机选择的实物期权随机变量模型[J].铁道学报,2008,30(6):13-18.

[4] 唐文彬,张飞涟,马超群.基于模糊实物期权的城市轨道交通项目投资价值[J].系统工程,2011,29(12):110-115.

[5] Doan P, Menyah K. Impact of irreversibility and uncertainty on the timing of infrastructure projects [J]. Journal of Construction Engineering and Management, 2013, 139(3): 331-338.

[6] De Jong M, Mu R, Stead D,. Introducing public-private partnerships for metropolitan subways in China: what is the evidence? [J]. Journal of Transport Geography, 2010, 18(2): 301-313.

[7] Phang SY. Urban rail transit PPPs: Survey and risk assessment of recent strategies [J]. Transport Policy, 2007, 14(3): 214-231.

[8] Chang Z. Public-private partnerships in China: A case of Beijing No. 4 Metro line [J]. Transport Policy, 2013, 30: 153-160.

[9] Shen LY, Li H, Li QM. Alternative concession model for build operate transfer contract projects [J]. Journal of Construction Engineering and Management, 2002,128 (4): 326-330.

[10] Shen LY, Wu YZ. Risk concession model for build operate transfer contract projects [J]. Journal of Construction Engineering and Management, 2005, 131(2): 211-220.

[11] Wu M, Chau KW, Shen QP,. Net asset value-based concession duration model for BOT contracts [J]. Journal of Construction Engineering and Management, 2012, 138(2): 304-308.

[12] 刘伟,吕俊娜,邹庆.收益不确定下交通BOT项目特许期决策模型[J].系统工程,2012,30(12):51-56.

[13] 吴孝灵,周晶,洪巍.基于有效运营期的BOT项目特许权期决策模型[J].系统工程学报,2011,26(3):373-378.

[14] 王东波,宋金波,戴大双,等.弹性需求下交通BOT项目特许期决策[J].管理工程学报,2011,25(3):116-122.

[15] Shen LY, Bao HJ, Wu YZ. Using bargaining-game theory for negotiating concession period for BOT-type contract [J]. Journal of Construction Engineering and Management, 2007, 133(5): 385-392.

[16] 鲍海君.基础设施BOT项目特许权期决策的动态博弈模型[J].管理工程学报,2009,23(4):139-141.

[17] Hanaoka S, Palapus HP. Reasonable concession period for build-operate-transfer road projects in the Philippines [J]. International Journal of Project Management, 2012, 30(8): 938-949.

[18] Li WX, Yin S. Analysis on cost of urban rail transit [J]. Journal of Transportation Systems Engineering and

[19] Information Technology, 2012, 12(2): 9-14.

[20] 陈进杰.地铁次优定价模型研究[J].北京工业大学学报,2011,37(11):1644-1649.

[21] 叶苏东.BOT模式开发城市轨道交通项目的补偿机制研究[J].北京交通大学学报(社会科学版),2012,11(4):22-29.

[22] Peskir G, Shiryaev A. Optimal Stopping and Free Boundary Problems [M]. Switzerland: Birkhäuser Basel press, 2006.

[23] Dixit A, Pindyck RS. Investment under Uncertainty [M]. Princeton: Princeton University Press, 1994.

[24] Cruz CO, Marques RC. Flexible contracts to cope with uncertainty in public-private partnerships [J]. International Journal of Project Management, 2013, 31(3): 473-483.

Cooperative Game Model on Concession Period in SBOT Project under Uncertainty

LV Jun-na1, 2, LIU Wei1, ZOU Qing1,GAN Lin3

(1. School of Economics and Business Administration, Chongqing University, Chongqing 400030, China;2. School of Management, Chongqing Jiao Tong University, Chongqing 400074, China;3. School of Construction Management and Real Estate, Chongqing University, Chongqing 400045, China)

As an effective solution to the problems of traffic congestion and emissions, urban rail transit has become China's key construction and investment fields. The shortage of capital is one of the biggest obstacles to restricting the development of urban rail transit.Subway line 4 in Beijing introduced a new form of BOT procurement model, namely SBOT (Subsidize in Building, Operate, and Transfer) model. Now, the SBOT procurement model has been widely adopted, such as subway line 4 in Beijing, subway line 14 in Beijing, subway line 1 in Hangzhou, etc.Concession period is one of the crucial decision variables in the arrangement of urban rail transit SBOT-type contracts.Projects with a shorter concession period could result in a higher toll/tariff regime transferred to the group of people who use the infrastructure facility. On the other hand, granting an excessively long concession period may result in government’s loss. Since urban rail transit SBOT projects are characterized by irreversibility and uncertainty, project values tend to be underestimated by ignoring the value of the option to defer in the evaluation process. Therefore, concessionaire requires long concession periods. Therefore, the option to defer should be included when determining a reasonable concession period of SBOT projects under uncertainty.Existing literature for urban rail transport SBOT pattern is still in the exploratory stage, which has yet to see reports of right SBOT quantitative research on concession periods. However, the existing literature on the quantitative study of the concession period focuses on traditional BOT projects and is based mainly on the combination of net present value (NPV) method and game theory. The NPV method, however,cannot properly capture managerial flexibility value in SBOT projects. Besides, none of these decision-making models addresses additional social benefits or costs that BOT project may present. Urban rail transit is considered a green transportation with many tangible and social benefits, such as energy saving, safe, comfort, fast and efficient. Therefore, the quantitative study of the concession period should consider both economic and social benefits associated with urban rail transit projects.To overcome the limitations of the existing decision making models on concession-period, this research presents an alternative method to defining the concession period for SBOT projects using real options and cooperative game theory, as well as considering both economic and social benefits. The optimal concession period can be identified through two procedures: First, classical irreversible investment models, which view investment opportunities as perpetual American call options, are used to construct decision-making models of public sector/private sectors on investment in SBOT projects under dynamic uncertainty. A feasible interval for concession period is determined. Furthermore, the research sets concession periods as a decision variable, develops the real option model based on extended NPV function, and proposes a cooperative game model to maximize the sum of the two party’ payoff functions. The paper derives the equilibrium solution in cooperative game. Finally, an example of urban rail transit SBOT project is applied to demonstrate the decision-making model of concession period under uncertainty. This research provides a new perspective and a reference for the public and private sectors to determine the equilibrium solution of concession periods for urban rail transit SBOT projects.

SBOT project；concession period；real option；extended net present value

中文编辑：杜 健；英文编辑：Charlie C. Chen

F294

A

1004-6062(2016)03-0209-07

10.13587/j.cnki.jieem.2016.03.026

2013-10-09

2014-03-11

中央高校基本科研业务费科研专项人文社会科学类资助项目（CDJSK100155）

吕俊娜（1981—），女，山西运城人；重庆大学经济与工商管理学院，技术经济及管理专业博士研究生，重庆交通大学管理学院，讲师，主要从事特许经营项目投融资决策研究、城市与市政经济研究。