基于模糊聚类筛选和交通可达性的心血管医院选址布局研究
2016-10-14韩振军焦建彬
赵 韡,韩振军,焦建彬
基于模糊聚类筛选和交通可达性的心血管医院选址布局研究
赵 韡,韩振军,焦建彬
(中国科学院大学,北京,100049)
心血管病(CVD)正在成为当今影响我国居民健康的主要威胁,如何通过构建重点心血管病防治一体化网络,从而有效地对其进行预防和控制成为当务之急。该问题可归结为选址问题,以前的研究成果要么定性的从多属性中评估候选地址并对其进行排序,要么定量建立目标函数求解最优结果。然而地址的选择问题,尤其对于医院这类不仅要考虑医院自身各项指标,同时也要考虑其他影响(如群众方便性等)的复杂问题,求解方式应该是定性和定量综合评估和优化的过程。所以,本文在理论上首次把定性和定量(交通可达)模型融合在一起用于解决医院选址的问题。首先使用模糊聚类的方法,定性的根据医院的各项指标筛选出能够满足目标的合格医院;其次,在从空间分布(即交通可达性)角度建立目标函数优化模型,定量的从所有合格的医院当中确定最终的入围医院。通过两步筛选既保证了医疗资源的优质性,又能从空间上兼顾医院地理上的布局,同时还引入了权重参数,方便决策者对结果进行修正。文章最后结合我国的实际情况进行案例分析,为心血管病医院的选址布局提供决策依据和方法参考。
心血管病;医院选址;模糊聚类
0引言
目前,心血管疾病已经成为全球面临的问题,其“发病率高、致残率高、死亡率高、复发率高,并发症多”—“四高一多”的特点[1],使之成为全世界面临的重大公共卫生乃至社会问题,且在发展中国家亦日益突出。在我国,心血管疾病死亡率长期居于首位,高于肿瘤及其它疾病[2]。近几年来由中国医学科学院阜外心血管医院和首都医科大学附属北京安贞医院-北京市心肺血管疾病研究生与美国哥伦比亚大学合作完成的中国冠心病预测模型是目前针对我国国内心血管发病预测模型中功能最全面的一个模型。报告中的模型指出,中国国内由于人口老龄化、高血压、高血脂、吸烟等诸多因素,到2030年中国男性的心血管发病率会增加13%,女性增加14%[2]。
由于心血管疾病的严重性、普遍性和高病死率,卫生保健体系亟待采取各种措施降低心血管危险的发生和加大相关医疗资源的投入[4]。现代心血管医院的选址布局,对于构建完整合理的心血管病防治一体化网络、优化地区医疗资源的配置至关重要。心血管医院的防治一体化网络布局建设指的是把上级大中型医院与社区卫生服务中心医院(简称社区医院)二者结合起来的二级网络模式,主要用于防范和治疗心血管疾病。该网络主要以防治基本原则为依据,“发展优势, 改善劣势、抓住机遇、避免威胁”为指导原则,全面构建心血管病防治战略体系,打通防治各个环节,建立防治网络,充分发挥各级医疗机构在防治体系中的作用,提高心血管病防治医疗服务能力。具体来说,应该由顶层根据各区域的发病率、人口分布特点、医院接诊能力及交通便利程度等因素,遴选出区域重点心中心医院,划分社区医疗机构归属,明确各级医疗机构防治职责与任务,形成国家主抓重点医院、重点医院指导社区、社区负责居民的层级管理网络。大中型医院是网络的中心,可以从众多现有医院当中挑选出合适的几家[5]。社区卫生服务中心是对接单位,向上可以对接中心医院的资源,向下可以直接面向居民用户。网络建设的成本主要是中心医院的资源和人员配置管理的费用。因而,采用科学有效的方法对大中型医院进行选址布局,可以降低建设成本,高效公平的为居民提供医疗资源。同时对发挥重点心血管医院的作用、保障患者生命健康以及促进医疗卫生系统的平衡快速发展也有重要意义。
然而,构建心血管病防治一体化网络,对心血管医院进行选址布局是一个复杂的问题,既要考虑各个医院的客观指标,也需要考虑群众出行的方便性,结合定性和定量方法进行综合的分析。对于决策者来说,他们既希望客观快速的筛选医院,又常常需要人为的调节结果。于是找到一个融合定性定量分析,同时又能动态可调节的模型成为当务之急。
1 相关研究
对于选址布局问题而言,传统的做法大致可以分成2类,即定性和定量。定性主要通过对地址的主观或客观打分,最后获得最优的方案,如以下几篇文章。文献[6]使用了要素权重排序的方法,采用了多种不同要素评估的测量,一些要素是使用主观评分,另一些是主观排序,最后通过这些评判结果对所有地址进行打分排序挑选出排在前面的地址。文献[7]中所有的要素根据主观和客观特性进行分组,关键的要素权重更高,最后通过对这些地址的得分选出候选方案。文献[8]使用对不同属性评估其效用值的方法,并给出核电选址的例子。文献[9]使用对目标分配权重的方法,不同的目标根据模糊集合理论进行定义,把一个线性问题转换成了非线性问题。文献[10]使用模糊数学的相关理论对不同的属性进行评估,该模型可以评估一些非精确描述的属性。文献[11]使用语言描述的方案来评估主观属性,并给出了一个简单的基于模糊聚类的方法。文献[12]使用三角模糊隶属度来评估不同权威决策者的分析结果,最后根据模糊适性指数排序不同的地址。文献[13]使用了三重标准评估方案,即最大最小、最小最大、最小和,用于评估凸型区域的选择。文献[14]使用模糊多目标的方法建模,并引入遗传算法进行求解,这篇文章首次将模糊集合和遗传算法结合在一起求解选择问题。文献[15]根据语言描述来排序不同的候选地址,使用了模糊集合理论。文献[16]使用了三个偏好模型来评估不同的候选地址。另外,文献[17][18][19][20][21]在决策的目标函数中加入了不确定性因素进行了研究。文献[22] [23] [24] [25]基于博弈论对选择问题进行决策。
定量分析主要采用数值优化的方案,根据目标函数求解最优值,而目标函数通常为成本最小函数。文献[26]的整型规划是对以医疗资源的可接近性与资源在地区内的平均分布性作为约束的双目标函数进行求解。文献[27]中P-中值问题是指选定p个设施的位置,使最坏的情况达到情况最优。文献[28]中选址的目标函数主要基于商品价格和到市场的距离,这是首次提出这种基于花费函数的选址决策理论。文献[29]地址的选址考虑了运输、人力和工业分布等成本,由于这个模型并没有考虑地价等因素,因而相对比较简单。文献[30]选址模型考虑了利润而并非只有成本花费,最终目标是让利润最大化。文献[31]使用优化模型来评估厂站的选址,考虑的因素包括交通和资源等,不过文章的前提假设过于简单。文献[32]选址使用了电势点的概念。
以上的选址方案理论研究成果要么定性的从多属性中评估候选地址并对其进行排序,要么定量建立目标函数求解最优结果。其实地址的选择问题,尤其对于医院这类不仅要考虑医院自身各项指标,同时也要考虑其他影响(如群众方便性等)的复杂问题,求解方式应该是定性和定量综合评估和优化的过程。所以,本文在理论上首次把定性和定量(交通可达)模型融合在一起用于解决医院选址的问题。具体来说,本文采取两步决策的步骤。首先使用模糊聚类的方法,定性的根据医院的各项指标筛选出能够满足目标的合格医院;其次,在从空间分布(即交通可达性)角度建立目标函数优化模型,定量的从所有合格的医院当中确定最终的入围医院。通过这两个过程,我们一方面可以保证优秀的医院资源得到合理利用,另一方面又考虑了交通便利,方便了各社区医院到中心医院的便利性。同时还引入了权重参数,方便决策者对结果进行修正。在目前我国医患关系问题突出的背景下,使用本文的两步方法决策,可以充分体现对人民群众的重视,也展现了以人为本的决策思路。文章最后用真实数据求解模型并得出了结果。
2 问题描述和建模思路
2.1 问题描述

图1 心血管医院选址问题空间描述
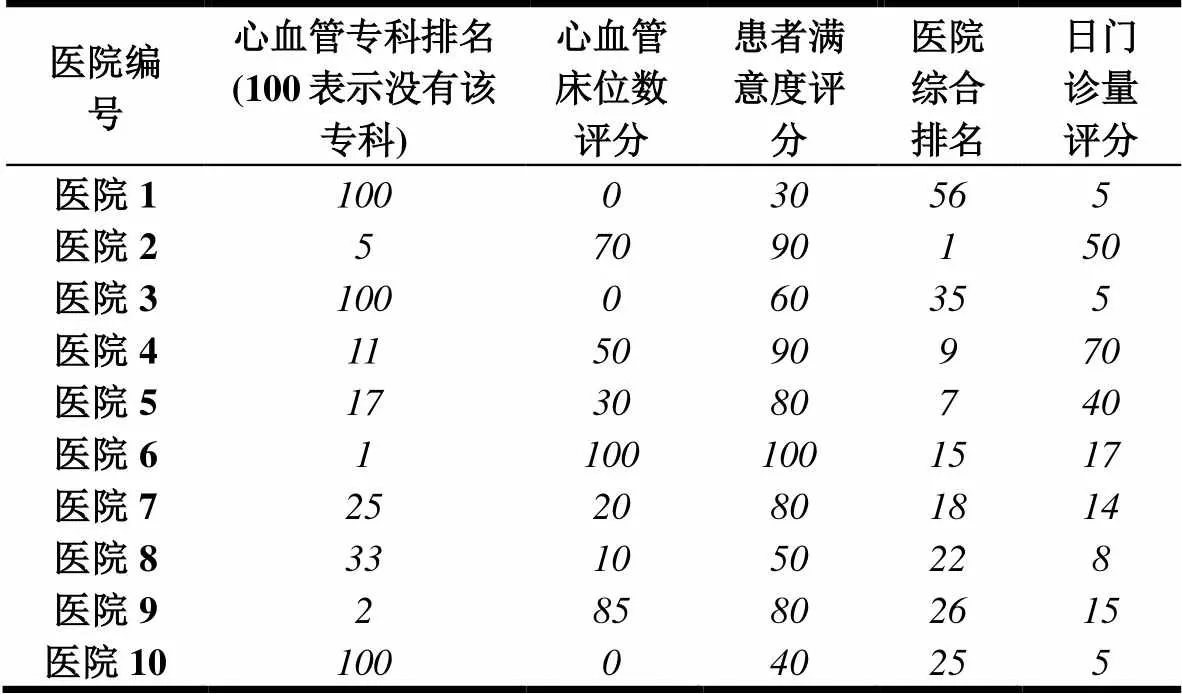
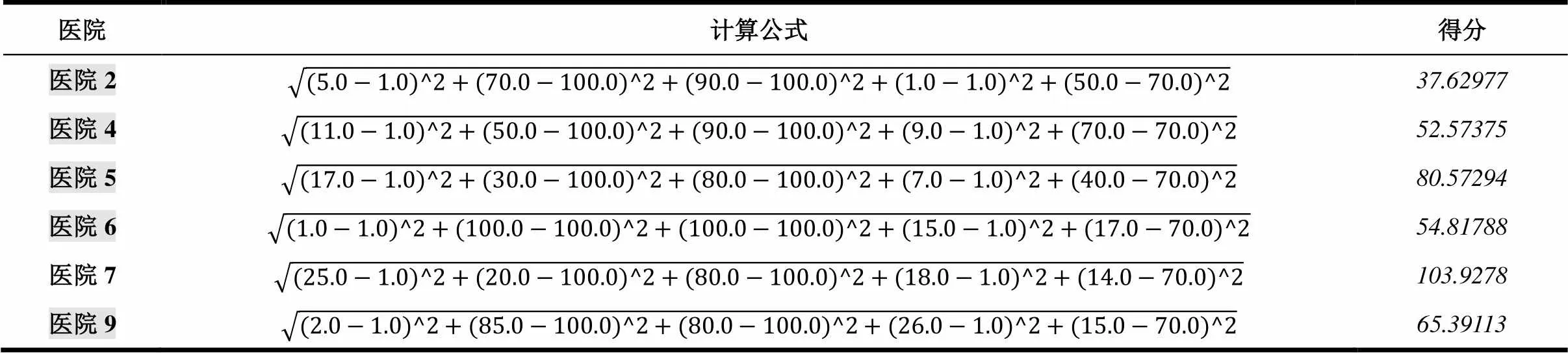
问题的描述如图1所示,该城市有候选的n家医院(十字),问题的目标就是要从这n家医院当中选出b家来构建心血管防治一体化网络的中心医院,同时该网络布局使得社区医院(居民)交通上最为便利,使各社区医院(圆圈)可以方便到达网络里某一家中心医院即可。于是,本文选址的方法主要分成两步,第一步根据医院的各项指标用模糊C均值聚类方法把医院分成两类,一类是合格,另一类是不合适,然后从合格的医院里筛选取得分最高的h个医院作为第二步的输入;第二步通过交通可达模型确定医院最终选址布局(从h家合格医院里选出b家,b 2.2 建模思路 医院地址的选择问题需要把定性和定量模型结合在一起。首先,我们假设候选的医院是m维空间的对象,每一维空间代表某一属性或指标。首先我们采用定性的方法,根据医院本身的属性或指标进行聚类,找出合格的医院集合。接着,对于空间分布这个比较中性的属性,可以采用定量的方法,建立交通可达目标函数,再从这些合格医院当中找出最优的医院布局。 2.3 定性筛选原则 考虑哪些因素来筛选医院非常重要,一般来说,选址的因素可以分成两类,即主观因素和客观因素。对于主观因素,我们主要用定性的方式来描述,如差、一般、非常好等。而对于客观因素则可以使用定量的方式来描述,如年门诊人数等。医院的筛选应该综合考虑主观因素和客观因素。由于本文是针对心血管疾病的医院进行选择,因而客观上需要考虑心血管专科的排名和心血管床位数,这是最能代表该专科能力的两个指标。另外,也需要考虑医院的综合影响,所以把日门诊量和综合排名也考虑进来。最后,患者的满意度也是医院评估的重要考量,这是一个主观的因素。综上分析,我们主要考量以下5个因素 1)心血管专科排名 2)心血管床位数 3)患者满意度 4)日门诊量 5)医院综合排名 考虑到不同因素的值区间不一致,我们最终通过归一化处理,把这5个因素的值映射到数值0-100之间。 另外,考虑到各要素对医院的评估贡献是不一样的,我们引入要素分配权重,区间为[0,1],值越大表示越重要。不同的权重使得各要素归一化处理的过程中可以得到不同的权值。这样我们分配好各权重值后,便可以在后面的距离值计算模型中对各要素直接相加和对比。归一化公式如下 max为该指标样本数据的最大值,min为该样本数据的最小值。就是样本数据,为归一化后的值。为权重取值[0,1]。 2.4 定性筛选逻辑 通常对于数据的聚类依托于对象属性的内在关系,不同的内在关系可能会把数据分成1到n类。本文聚类筛选的目的主要是挑选出合格的医院,因而可以人为定义成两类,即“合格”与“不合格”。为了可以明确的区分哪一类是“合格”,哪一类是“不合格”,我们又人为的引入两个虚拟医院,即“最好医院”和“最差医院”。这两个虚拟医院的属性值就是从所有的候选医院对应的值中选择最好的值或最坏的值。经过模糊聚类后,包含“最好医院”医院的组就是合格的组。 2.5 定量优化机制 定量优化主要考虑的是医院的空间分布,对决策者来说就是交通可达性。交通可达性的不同对救治的及时性和人们的出行有很大的影响。而本文交通可达性的主要衡量方法就是计算社区医院到达某中心医院所花费的时间,时间越短我们认为交通可达性越好。衡量某家中心医院的交通可达性,我们可以计算不同社区医院到这家医院所花费的时间平均值。于是,建立一个目标函数,使得该方案下所得到的时间花费最小来选择出最后方案。 3.1模糊C均值聚类定性筛选模型 根据上一章节的分析,我们首先目标是把候选医院首先分成合格医院与不合格医院。具体方法就是加入两个虚拟的医院,一个是理想的合格医院(BestHospital),一个是最差的不合格医院(WorstHospital)。对于BestHospital,我们设置其所有的考虑因素得分是候选医院里最好的值,相反,对于WorstHospital,我们设置所有的得分都是最差的值。 根据模糊C均值模型[33],目标最小化以下目标函数 (3) 而每个集群的中心v用以下公式获得 n表示待分类的对象数目,m表示对象的维度(考虑因素数目),里面U表示聚类矩阵,是在聚类k的隶属度,是第k个对象,表示分类i聚类中心,c是聚类的数目,z是加权指数。 然后,根据合格医院集合,计算每个医院与BestHospital的距离值,并选取最高的h个医院作为第二步的输入。具体的距离值计算模型如下 3.2交通可达定量优化模型 根据上面模型的结果,我们选取了h家得分最高的医院,但并没有考虑他们的空间布局。所以接下来,我们通过交通可达模型从这h家中选出b家作为最终的方案。考虑到选出的这h家合格医院也有不同,决策者有时需要人为调节结果或人们有时也不管距离多远都会去某家中心医院看相关疾病,于是我们引入权重值来表示医院j的权重以区分不同医院的重要性。的本质就是把重要医院的距离(可达时间)缩短,这样可以统一归结到可达时间这一个目标上来。 首先,我们以最短可达时间作为交通可达模型的评价指标,于是各社区医院到中心医院的平均可达时间的模型为: p为统计的社区医院数目 根据公式(6),我们就可以评估某方案X(b个医院集合)的交通可达指标值,具体如下 Max(8) 3.3模型求解 3.3.1模糊C均值聚类模型求解 我们假设候选的医院为n家,评价的要素为m个,第一步的目的是从这n家医院选出h(h<=n)家合格的中心医院。于是对每个医院每个因素评分,可以形成一个n*m的矩阵。第k个医院的第j因素的评分用表示,0 1) 初始化矩阵U 3) 利用如下公式(9)更新聚类矩阵 5) 根据公式(5)的结果计算合格的医院评分,然后根据评分选出前h家医院作为结果 3.3.2交通可达模型求解 求解通过O-D矩阵分析获得,我们借助ArcGIS的网络分析模块。具体做法就是通过公式(8),从可行的候选方案集合X中选择一个方案,并把这方案中的合格医院作为目的点设置在地图上;另外设置典型的p个社区医院作为起点。同时设置每条道路的通行时间(公共交通和其他方式分别设置)。经过计算,我们可以得到p个社区医院到h个合格医院的通行时间,用矩阵p*h来表示。根据该矩阵,我们就可通过公式(6)计算交通可达指标值。最后求出最优的方案。 为验证模型和求解算法的有效性,本节根据前述分析,以北京的10所医院作为候选集为例(n=10),来计算最终方案。本文数据综合医院排名和专科排版来自HC3i中国数字医疗网,其他数据来自各医院的官方网站。实例当中,候选的医院有10家,我们的目标是从这10家医院当中选出3家作为最终的方案。b=3表示问题的目标是选出3家,由专家规划决定。 第一步,根据不同因素的值筛选出5家合格的医院,h=5表示总的集合的一半,因为我们最终把医院分组2组,best和worst,所以就取了中间值5。第二步再从这5家合格医院里选出交通可达的最优3家(b=3)。为了验证我们第二步模型中权重的有效性,我们先假设所有医院的权重值都为1,计算出对应结果。然后,根据实际情况认为某一家医院是必须入选的,我们把其权重改为10,然后再计算对应结果,并对比两次结果的不同。其他参数m=5,z=2,,因素表见表1(经过公式1归一化处理,权重设置都为1)。实质是医院的平均可达时间的模型中的时间倍数,等于1是表示时间不变,等于10时表示10倍的时间。这里设置10表示把该医院在平均可达时间修改为原来10倍,主要是为了显示出该系数改变后的效果,从地图上,设置到10倍距离肯定可以排除该医院。m=5表示5个评分要素。z=2是根据[35]中的试验结果得到,建议取值2。是算法结束的精度。 表1 10所医院候选集及因素评分 首先加入BestHostpital和WorstHopstal,见表2。 表2 BestHostpital和worstHopstal的因素评分 通过公式2,计算出聚类值,见表3。 根据聚类2排除不合格医院(聚类2中值>0.5,该值表示相似度,区间是[0,1],我们选择中间值0.5)1,3,8,10 医院。从排除结果来看,所有的没有心血管专科的医院(心血管专科排名=100,床位=0),即1,3,10这几家医院都被排除,而且他们的聚类值都非常高(大于0.9),符合常理,也进一步表明模型的正确性。 接着,根据聚类1选择合格的6(聚类1中值>0.5, 聚类2中值>0.5,该值表示相似度,区间是[0,1],我们选择中间值0.5)家医院,然后根据公式5计算合格医院的打分值如下表4所示。 表3 聚类评分结果 表4 合格医院打分结果 选择得分最小的5家医院2, 医院4, 医院5, 医院6, 医院9进入下一步。医院7被排除也符合预期,从专业排名上看,7的排名在这里面是最靠后的,同时,他的床位数也是最少的。 全北京(5环内)的社区医院大概有600家,而社区医院的分布一定程度上代表了患者的需求分布。为了考虑需求分布及简化模型计算,我们把时间精度控制在15分钟内,按照市区时速35公里计算,15分钟大概可以走9公里。因而我们把5环内区域(大概直径27公里)划分为3*3=9个区域,每个区域直径大概9公里。我们选取15家(平均大概50平方公里内一家)作为典型的社区医院作为计算依据,按照5环内大概有600家社区医院计算(社区医院的分布通过百度地图搜索社区医院得到),也就是每40家社区医院里面选取一家代表。这样我们可以根据9个区域包含的社区医院数目,决定每个区域有几家典型社区医院。 通过GIS,我们根据上面的说明,计算出典型的15(p=15)个社区医院作为起点,具体分布见图2,同时计算出到这5家中心医院的平均可达时间,=0.5(表示乘坐公共交通的比例为50%),t=45(表示到中心医院时间如果超过45分钟就不计入模型计算),如表5所示。 图2 五家合格医院及典型社区医院分布地图 表5 典型社区医院到中心医院平均可达时间 接着,利用公式(7)计算可能组合的交通可达值,如表6所示。 可见组合方案9是最优方案(得分86.78322最低),最后选择医院2,医院9和医院5,分布结果见图3。从图上看,比较集中的几家医院(6,2,4)我们只选取了一家,这样在整体上,2,9,5的分布性最好,可以更好的方便群众出行。 表6 交通可达得分 图3 不考虑权重指数的最终医院选取方案 但是,实际情况是医院6是必须入选的医院,因为其排名第一,是全国最好的医院,大家通常不考虑距离也会去,决策者也把它列入必选项。于是,我们改变模型中的权重系数。继续计算,结果如下: 方案序号医院组合得分 12,6,465.928024 22,6,961.402046 32,6,562.402046 46,4,962.781174 56,4,563.781174 66,9,559.255196 72,4,990.3092 82,4,591.3092 92,9,586.78322 104,9,588.16234 随着人们生活水平的提高,心血管疾病问题越发突出,因而构建心血管防治一体化网络,筛选出重点心血管医院成为亟待解决的问题。本文通过运用模糊聚类筛选合格医院,然后通过交通可达模型计算出最优的空间布局方案。从计算结果来看,该模型给出的选择结果与我们的预期基本一致,能给实际的选址工作提供一种全新的方法。主要优点如下 1)模型采用模糊聚类的方法,可以很方便的扩展候选对象的属性空间,因而对于需要考虑大规模维度的对象选择问题,使用该方法可以快速收敛得到有效值。 2)模型采用的分步计算的方法,因而可以很方便的对每一步的结果进行修正和验证。比如第一步计算的结果没有包括想要的医院,我们也可以人为加入想要的医院直接进入第二步优化计算。 3)模型引入了权重指数,使得可以更方便的人为修正结果成为可能。 虽然该模型取得了一定的效果,当将来还是可以从以下几个方面进行扩展或更深度的研究 1)文中心血管医院评价因素的选择是人工挑选的,在一定程度上存在主观性,因而将来可以对候选医院因素的选择也建立模型,使模糊聚类的方法更加有效。 2)文中第二步优化问题的计算是穷尽所有结果得到,对于大规模的计算有一定影响,可以在将来的研究当中引入遗传算法或其他算法。 总之,我们的模型对于实际工作有借鉴意义,能为国家和医疗机构的决策提供更精细化的参考工具。 [1] 杨捷. 社区居民心血管疾病相关危险因素调查研究[J]. 长春医学, 2007, 5(2): 11 [2] 卫生部. 中国卫生统计年鉴[M]. 中国协和医科大学, 2003. [3] Moran A, Gu D, Zhao D, et al. Future Cardiovascular Disease in China Markov Model and Risk Factor Scenario Projections From the Coronary Heart Disease Policy Model–China[J]. Circulation: Cardiovascular Quality and Outcomes, 2010, 3(3): 243-252. [4] 胡盛寿, 孔灵芝. 中国心血管病报告 2007[M]. 北京:卫生部心血管病防治研究中心, 2008: 2-34 [5] 王雪飞. 心血管病防治一体化进程渐渐提速[J]. 中国保健营养, 2005, 第2期:10-11. [6] Keeney R L, Raiffa H. Decisions with multiple objectives: preferences and value trade-offs [M]. Cambridge university press, 1993. [7] Brown P A, Gibson D F. A quantified model for facility site selection-application to a multiplant location problem [J]. AIIE transactions, 1972, 4(1): 1-10. [8] Kirkwood C W. A case history of nuclear power plant site selection [J]. Journal of the operational research society, 1982: 353-363. [9] Yager R R. Fuzzy decision making including unequal objectives [J]. Fuzzy sets and systems, 1978, 1(2): 87-95. [10] Narasimhan R. A FUZZY SUBSET CHARACTERIZATION OF A SITE‐SELECTION PROBLEM[J]. Decision Sciences, 1979, 10(4): 618-628. [11] Raoot A D, Rakshit A. A ‘fuzzy ‘approach to facilities lay-out planning [J]. The International Journal of Production Research, 1991, 29(4): 835-857. [12] Liang G S, Wang M J J. A fuzzy multi-criteria decision-making method for facility site selection [J]. The International Journal of Production Research, 1991, 29(11): 2313-2330. [13] Bhattacharya U, Rao J R, Tiwari R N. Fuzzy multi-criteria facility location problem [J]. Fuzzy Sets and Systems, 1992, 51(3): 277-287.. [14] Tzeng G H, Chen Y W. The optimal location of airport fire stations: a fuzzy multi‐objective programming and revised genetic algorithm approach[J]. Transportation Planning and Technology, 1999, 23(1): 37-55. [15] Chu T C. Facility location selection using fuzzy TOPSIS under group decisions [J]. International journal of uncertainty, fuzziness and knowledge-based systems, 2002, 10(06): 687-701. [16] CINAR D. FACILITY LOCATION SELECTION USING A FUZZY OUTRANKING METHOD[C]//Applied Artificial Intelligence: Proceedings of the 7th International FLINS Conference, Genova, Italy, 29-31 August 2006. World Scientific, 2006: 359. [17] 陈青丰, 鲁建厦, 刘敏. 非对称 AHP 方法在物流中心选址中的应用[J]. 工业工程, 2005, 8(1): 75-78. [18] 刘晓峰, 陈通, 柳锦铭, 等. 基于 ANP 的物流中心选址[J]. 工业工程, 2007, 10(5): 136-140. [19] LIU Xiaofeng, CHEN Tong, LIU Jinming, et al .The ANP based evaluation model and application of the site selection of logistics center [J]. Industrial Engineering, 2007, 10 (5): 136-140. [20] 谈英姿, 沈炯, 吕震中. 免疫优化算法及其前景展望[J]. 信息与控制, 2002, 31(5): 385-390. [21] TAN Yingzi, SHEN Jiong, LU Zhenzhong. Study of immune based optimization algorithm and its future development [J]. Information and Control, 2002, 31(5): 385-390. [22] 周华珍, 王花兰, 卢柏蓉, 等. 基于静态博弈论的物流配送中心选址优化研究[J]. 山东交通学院学报, 2014, 22(3): 31-34. [23] 李东, 晏湘涛, 匡兴华. 考虑设施失效的军事物流配送中心选址模型[J]. 计算机工程与应用, 2010, 46(11): 3-6. [24] 周洪超, 李海锋. 基于博弈论的电动汽车充电站选址优化模型研究[J]. 科技和产业, 2011, 11(2): 51-54. [25] 李如琦, 苏浩益. 基于博弈论的核电厂选址优化模型[J]. 电网技术, 2011, 35(2): 216-220. [26] P. Mitropoulos, I. Mitropoulos, I. Giannikos, A. Sissouras, A Bi-objective model for the location planning of hospitals and health centers [J]. Health Care and Management Science, 2006(9): P171-179 [27] Brandeau M, Sanfort F, Pierskallas W P. Operations research and health care: A handbook of methods and applications [M]. United States: Springer Publication, 2004. [28] von Thünen J H, Braeuer W. Der isolierte staat in beziehung auf landwirtschaft und nationalökonomie[M]. Fischer, 1960. [29] Giersch H. Economic union between nations and the location of industries [J]. The Review of Economic Studies, 1949, 17(2): 87-97. [30] Martin P, Rogers C A. Industrial location and public infrastructure [J]. Journal of International Economics, 1995, 39(3): 335-351. [31] Koopmans T C, Beckmann M. Assignment problems and the location of economic activities [J]. Econometrica: journal of the Econometric Society, 1957: 53-76. [32] Muther R, Webster D B. Plant Layout and Materials Handling [J]. Materials Handling Handbook, 2nd Edition, 1985: 19-77. [33] 高新波, 裴继红, 谢维信. 模糊 c-均值聚类算法中加权指数 m 的研究[J]. 2000. [34] 毛罕平, 张艳诚, 胡波. 基于模糊 C 均值聚类的作物病害叶片图像分割方法研究[J]. 农业工程学报, 2008, 24(9): 136-140. [35] Pal N R, Bezdek J C. On cluster validity for the fuzzy c-means model [J]. Fuzzy Systems, IEEE Transactions on, 1995, 3(3): 370-379. Fuzzy C Mean and Commute TimeBased Optimizing Locations of Cardiovascular Hospitals ZHAO Wei ,HAN Zhen-jun,JIAO Jian-bin ( University of Chinese Academy of Science (UCAS),Beijing 100049,China) Cardiovascular diseases have become a global problem, especially in developing countries. The long-term cardiovascular mortality is always one of top problems in China. In recent years, the Chinese Academy of Medical Sciences Fu Wai Hospital and other hospitals design a comprehensive heart disease prediction model. It is important to pay more attention to the problem because of the severity of cardiovascular diseases. To solve this problem, we must build an integrated model to prevent cardiovascular diseases. The integrated network consists of the centered hospitals and community health centers. Specifically, the centered hospital is chosen from a few hospitals in a city dealing with cardiovascular disseases . Community health center is the docking unit. How to use scientific and effective method to choose a right centered hospital is critical to the integrated network.The first part is the background and introduction. As for how to choose centered hospitals, the traditional approach can be divided into two types, namely qualitative or quantitative. Few articles integrate these two approaches. Therefore, this is the first article in the current literature trying to integrate qualitative and quantitative models in order to solve the problem for the chosen hospitals. Specifically, a two-step decision model is built in this article. First, we use fuzzy clustering methods, and qualitatively choose qualified hospitals to address our research questions. As a result, the utilization of hospital resources can be achieved. Finally, we solve the model with real data. The second part describes our modeling framework. First, we assume that candidate hospitals are located is m-dimensional space, with each dimension of the space representing one hospital. We then use qualitative methods to identify qualified hospitals. Next, quantitative method is used to find the best hospitals from the first step.The third part provides detail information about the model. For qualitative model based on fuzzy C-means clustering, our first goal is to choose qualified candidates. The method is to add two virtual hospitals: Best Hospital and Worst Hospital. For Best Hospital, we set all of its score from the best candidates. On the contrary, for Worst Hospital, we set all of its scores as the worst values. For transportation quantitative optimization model, we select final hospitals from the first step based on space distribution. Sometimes we need manual adjustments so that we can include weights into the hospital model. The fourth part is the result analysis and discussion. To verify the validity of the model, this section introduces 10 hospitals in Beijing as the candidate set. The ranking data is from HC3i Chinese digital medical network. Other data are collected from the official website of each hospital. Our goal is to choose 3 hospitals as the final solution from these 10 hospitals. In the first step, we identify 5 qualified hospitals. Afterwards, we select the final 3 hospitals from based on the analysis in the second step. After checking the result with the real map, we believe this model is as good as we expected.The fifth part is the conclusion. The main advantages are summarized as follows. First, the model uses fuzzy clustering which can be easily extended to analyzing similar problems in large-scale dimensions. Secondly, the method uses a two-step model so that it is convenient to adjust and verify each step’s result. For example, the results of the first step in the calculation do not include hospitals we want. Instead, we artificially add one hospital directly to the hospital list of the second step. Third, the model introduces weights parameters, making it easier for us to adjust the model. cardiovascular hospital; optimizing location; fuzzy c mean 中文编辑:杜 健;英文编辑:Charlie C. Chen O223 A 1004-6062(2016)03-0202-07 10.13587/j.cnki.jieem.2016.03.025 2015-10-09 2016-01-04 国家科技支撑计划课题(2011BAI11B02) 赵韡(1974—),男,北京人;中国科学院大学在读博士,高级工程师,研究方向:生物医学工程,医学信息学。
3 模型建立和求解




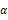


4 结果分析与讨论







5 结论
