Hermite-Hadamard不等式推广的q-模拟
2016-10-14时统业李照顺
时统业, 李照顺, 夏 琦
(海军指挥学院信息系, 南京211800)
Hermite-Hadamard不等式推广的q-模拟
时统业,李照顺,夏琦
(海军指挥学院信息系, 南京211800)
利用凸函数和q-积分的定义和性质,给出Hermite-Hadamard不等式一个推广的q-模拟.分别在q-导数的绝对值是凸函数、q-导数有界这两种情况下,给出由此q-模拟所产生的差式的估计.
q-积分;q-导数;q-Hermite-Hadamard不等式; 凸函数
1 引 言
若f是区间I上的凸函数,则对任意a,b∈I,a (1) 式(1)就是著名的Hermite-Hadamard不等式[1]. 关于式(1)的各种推广和加细以及各种类型凸函数的Hermite-Hadamard型不等式,请参阅文献[2] . 引理1[3]设f(x)为区间I上的凸函数,则f(x)在开区间(a,b)⊂I内处处存在左、右导数(从而处处连续),且对x,y∈(a,b),x 近些年,量子积分不等式引起许多学者的兴趣[4-11],其中文献[7]给出连续凸函数的q-Hermite-Hadamard不等式. 定义1[9]设f:[a,b]⊂→是连续函数,x∈[a,b],则称 为f在x处的q-导数. 定义2[5]设f∶[a,b]⊂→是连续函数,x∈[a,b],则f的Riemann型q-积分定义为 若c∈(a,x),则f的q-积分定义为 引理2[8]设f,g∶[a,b]⊂→是连续函数,α∈,则对任意x∈[a,b]有 证由q-积分定义可证明,这里略去. 引理4[9]设α∈{-1},则有 引理5[7](q-Hermite-Hadamard不等式)设f∶[a,b]⊂→是连续凸函数,则有 (2) 王良成在文献[12]中给出式(1)的如下推广: 定理1[12]设f是[a,b]上的连续凸函数,p∈(0,1),ξ=pa+(1-p)b,则 (3) 文[10]在q-导数的绝对值是凸函数的情况下,给出由式(2)右端部分所产生的差式的估计.本文将给出式(3)的q模拟,并仿照文[10]的方法,分别在q-导数的绝对值是凸函数、q-导数有界这两种情况下,给出由式(3)左端部分和右端部分所产生的差式的估计.当q→1时,我们得到已有文献的结果. 为方便起见,引入下面记号: 为证明本文的主要结果,需要下面涉及q-积分的恒等式和一些多项式的q-积分. (4) 证不妨设 则由引理2和引理3得 (5) (6) 证类似于引理6证明,这里略去. 引理8设0 ≤pf(a)+(1-p)f(b). (7) 证由凸函数的定义,对任意x∈[a,b],有 (8) (9) 对式(8)和式(9)中的x在[a,b]上求q-积分得 (10) (11) 由引理1,对任意x∈[a,b]有 (12) (13) 对式(12),(13)中的x在[a,b]上积分得 (14) (15) 其中利用了下面事实: ≤pf(a)+(1-p)f(b). 证在定理2中令q→1即可得证. |I(a,b;p,q;f)| (16) 利用引理8,式(16)得证. 注2设|f′|是[a,b]上的凸函数,在定理3中令q→1,则由式(16)得 特别地,当p=1/2时,得到下面梯形不等式[13] 定理4设f∶[a,b]→是连续函数,和在[a,b]上可积,且,则有 (17) 利用引理8,式(17)的右端部分得证.同理可证式(17)的左端部分. 注3设m≤f′≤M,在定理4中令q→1,则由式(17)得 特别地,当p=1/2时得到下面的梯形不等式[14] 定理5设f∶[a,b]→是连续函数,和是[a,b]上的凸函数且可积,则有 (18) 证类似于定理3证明,这里略去. 注4设|f′|是[a,b]上的凸函数,在定理5中令q→1,则由式(18)得 特别地,当p=1/2时,得到下面的中点不等式[15] 定理6设f∶[a,b]→是连续函数,和在[a,b]上可积,且,则有 (19) 证与定理4的证明同理可证,这里略去. 注5设m≤f′≤M,在定理6中令q→1,则由式(19)得 特别地,当p=1/2时,得到下面的中点不等式[16] [2]Dragomir S S,Pearce C E M.Selected Topics on Hermite-Hadamard inequalities and applications[DB]. http:∥rgmia.vu.edu.au/SSDragomirweb.html. [3]刘三阳,李广民.数学分析十讲[M].北京:科学出版社,2011:89. [4]Ernst T.A comprehensive treatment ofq-calculus[M].Basel: Birkhauser,2012. [6]Gauchman H. Integral inequalities inq-calculus[J].Comput.Math.Appl., 2004(47):281-300. [8]Tariboon J,Ntouyas S K.Quantum calculus on finite intervals and applications to impulsive difference equations[J]. Advances in Difference Equations,2013:282. [9]Tariboon J,Ntouyas S K.Quantum integral inequalities on finite intervals[J].J.Inequal.Appl.2014:121. [10]Sudsutad W,Ntouyas S K,Tariboon J.Quantum integral inequalities for convex functions[J].Journal of Mathematical Inequalities,2015,9(3):781-793. [11]Noor M A,Noor K I,Awan M U.Some quantum estimates for Hermite-Hadamard inequalities[J].Applied Mathematics and Computation,2015(251):675-679. [12]王良成.凸函数的Hadamard不等式的若干推广[J].数学的实践与认识,2002,32(6):1027-1030. [13]Dragomir S S, Agarwal R P.Two inequalities for differentiable mappings and applications to special means of real numbers and trapezoidal formula[J].Appl.Math.Lett., 1998,11(5): 91-95. [14]Barnett N S, Dragomir S S.Applications of Ostrowski’s version of the Grüss inequality for trapezoid type rules[J]. Tamkang J.Math., 2006, 37(2): 163-173. [15]Kirmaci U S.Inequalities for differentiable mappings and applications to special means of real numbers and to midpoint formula[J].Applied Mathematics and Computation , 2004(147): 137-146. The q-analogue of a Generalization of Hermite-Hadamard Inequality SHITong-ye,LIZhao-shun,XiaQi (Department of Information,PLA Naval Command College,Nanjing 211800, China) Starting from the definition and basic properties of convex functions andq-integral,theq-analogue of a generation of Hermite-Hadamard inequality is obtained.The estimates of the difference generated by theq-analogue are given when the absolute value ofq-derivative is convex function orq-derivative is bounded. q-integral;q-derivative;q-Hermite-Hadamard inequality; convex function 2016-01-11;[修改日期]2016-05-20 时统业(1963-),男,硕士,副教授,从事基础数学教学与研究.Email:shtycity@sina.com O178 A 1672-1454(2016)03-0030-07





















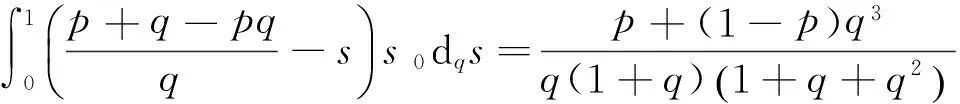





2 主要结果




























