离散交易框架下TIPP策略收益保证的定价研究
2016-10-14刘海龙
张 飞,刘海龙
离散交易框架下TIPP策略收益保证的定价研究
张 飞,刘海龙
(上海交通大学安泰经济与管理学院,上海 200052)
TIPP策略是收益保证类金融产品所采用的主要交易策略之一。文章分别采用几何布朗运动与有限跳跃Levy过程来刻画风险资产的价格过程,并对离散交易框架下的TIPP策略收益保证进行定价。由于TIPP策略下投资组合市值过程的复杂性,文章无法得到收益保证的解析定价公式。文章给出了离散交易框架下TIPP策略的一个特例下的封闭定价公式。数值分析的结果表明:离散交易条件下,(1)无论是否存在价格跳跃及借款限制,TIPP策略收益保证均存在缺口风险,收益保证的价格大于0;(2)与传统连续价格路径情形相比,价格跳跃条件下TIPP策略收益保证价格更高;(3)TIPP策略收益保证的价格与策略乘数、收益保证水平、杠杆比率以及调整周期正相关,与价值底线百分比负相关;(4)借款限制会降低TIPP策略收益保证的价格,且该效应随着策略乘数、收益保证水平、杠杆比率以及调整周期的增加而增强,随着价值底线百分比的上升而减弱。
离散交易;TIPP策略;有限跳跃Levy过程;收益保证;缺口风险
0 引言
固定比例投资组合保险(constant proportion portfolio insurance, CPPI)策略是一种动态投资组合管理技术,该技术旨在对投资组合进行保护并使得投资者能够在上升市场行情中的获取部分收益①CPPI由Perold[1]针对固定收益市场提出,Black和Jones[2]与Black和Perold[3]将其扩展到权益市场。由于CPPI策略为投资者实现既定保值目标提供了易于操作的工具而为广大投资者尤其是机构投资者所青睐。CPPI策略广泛应用于收益保证类金融产品市场。尽管CPPI策略具有简单、可控以及富有灵活性等优点,该策略只能对本金进行保护,而未能对投资期内的收益进行保护。针对CPPI策略的不足,Estep和Kritzman[4]建议应该在市场处于上升行情中提高策略价值底线(floor)以便对投资期间的收益进行保护,并提出了时间不变投资组合保护(time-invariant portfolio protection, TIPP)策略。假定市场资产价格是连续变化的且可以无成本地连续交易,运用CPPI策略与TIPP策略对投资组合进行保护,不会出现到期不能兑现收益保证承诺的情形:即不存在缺口风险(gap risk)。 但当资产价格出现非连续变化(跳跃)或由于流动性、交易成本等因素而不能连续交易时,运用以上两种策略可能会面临缺口风险[3-6]。当出现缺口风险时,运用CPPI策略与TIPP策略的收益保证类金融产品的发行与管理机构会请第三方进行担保或向第三方购买保险。如何确定一个合适的担保费用(率)或保险费用(率)是一个十分重要的现实问题。
目前,国内外的相关定价研究主要是针对CPPI策略的。离散交易框架下对CPPI策略收益保证的定价研究主要有Hamidi等[7],Balder等[8]以及Paulot和Lacroze[9,10]。Hamidi等[7]对CPPI策略进行了扩展,允许策略乘数随时间变化,并将策略乘数设定为扩展期望在险价值(extended expected Value-at-Risk)的函数。Hamidi等[7]分别采用参数、半参数以及非参数方法对条件乘数模型进行了估计并运用期权估值方法对条件乘数与非条件乘数模型下的缺口风险进行了度量。Balder等[8]提出了一种离散时间版本的CPPI策略,该策略满足三个条件:自融资性、风险敞口非负以及投资组合市值过程是收敛的。Balder等[8]证明了在离散调整条件下,如果风险资产价格服从几何布朗运动(geometric Brownian motion,GBM),那么CPPI策略收益保证存在封闭形式的定价公式。Paulot和Lacroze[9]采用马科夫算子(Markov operator)来对CPPI策略收益保证进行定价。当风险资产价格服从齐次过程(homogeneous process)条件下,路径依赖的CPPI策略可以被重新表述为一个单变量马科夫过程。Paulot和Lacroze[9]对CPPI策略欧式与美式收益保证进行了定价并考察了各种特征(风险资产模型、乘数、最大风险敞口、最小风险敞口、缓冲额限制、期间收益锁定以及门限值)对CPPI策略收益保证缺口风险的影响。Paulot和Lacroze[10]证明了如果风险资产价格服从一个独立增量过程(process with independent increments),那么CPPI策略投资组合在离散调仓时点上的市值过程可以用一个离散时间的单变量马科夫过程来描述,并且可以通过转移概率(transition probabilities)来建立高效定价机制。连续时间市场环境下与CPPI策略收益保证定价相关的研究主要有Cont和Tankov[6]。Cont和Tankov[6]在价格跳跃与随机利率条件下考察了CPPI策略的一个特例:即不考虑借款限制或允许卖空无风险资产情形下的CPPI策略,并给出了该策略的触底概率、期望损失以及损失的分布。Cont和Tankov[6]证明了在无借款限制与常利率条件下,如果风险资产价格存在跳跃那么即便投资者可以连续交易,缺口风险总是存在的。国内有关CPPI策略收益保证定价的研究非常少,公开可得的仅有王亦奇和刘海龙[11]。王亦奇和刘海龙[11]采用纯扩散模型来刻画风险资产与无风险资产价格过程,采用Vasicek[12]模型来描述市场瞬时短利率,并在此假定下考察了CPPI策略收益保证的定价问题。尽管TIPP策略在业界应用广泛,但目前国内外还未有对TIPP策略收益保证进行定价研究的文献。本文分别采用GBM与有限跳跃Levy过程来对风险资产价格过程进行刻画,并在离散交易假定下考察了TIPP策略收益保证的定价问题,该研究是对已有相关研究的补充与拓展。
本文余下部分结构安排如下:第1部分给出了离散交易框架下TIPP策略收益保证的定价模型;第2部分给出了收益保证定价的数值分析结果;第3部分则对全文进行了总结。
1模型
1.1市场假定
假定市场中有两种资产可供交易:风险资产与无风险资产。假定风险资产为未派发股利的股票,无风险资产为期限为T面值为G的零息票债券。假定市场短利率r是固定不变的。零息票债券价格过程B(t,T)(以下简记为B(t))为
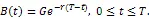
假定风险资产的价格过程S(t)由以下随机微分方程刻画
(2)
其中,L(t)是一个一维Levy过程,L(0)=0,该过程定义在带流概率空间上。P为真实世界概率测度。当L(t)为一带漂移的布朗运动时,S(t)服从Black-Scholes经济中的经典GBM假定;当L(t)既包含布朗运动成分又包含跳跃成分时,S(t)服从跳跃扩散模型。由于现实金融市场中资产收益分布多呈现出非对称尖峰厚尾特征(asymmetric leptokurtic feature),这使得蕴含正态收益分布的GBM模型难以真实地刻画资产价格过程。引入跳跃成分的跳跃扩散模型可以克服GBM模型的这一缺陷,已被广泛应用于金融相关领域的研究中。
由方程(2)可得到S(t)的表达式

(4)
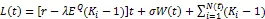
1.2离散时间TIPP策略
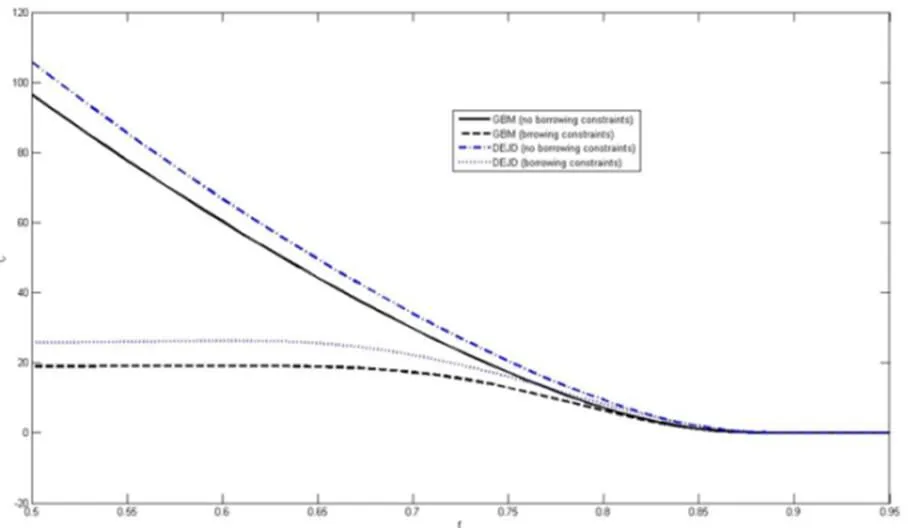
TIPP策略的基本原理是将资产的一部分配置在无风险资产上并将剩余部分资产或者称为缓冲额(cushion)加杠杆放大后投资在风险资产上,以期通过无风险资产取得本金的保护并通过风险性资产获取上升行情中的收益。为了对期间的收益进行保护,TIPP策略则提出对CPPI的价值底线(floor)进行修改使之棘轮上升(ratchet up),即在上升行情中提高价值底线,而在下行行情中保持原来的价值底线。假定投资期限为T,投资期初的资金为A0,收益保证水平为G,TIPP策略的乘数记为m,m>1。TIPP策略的价值底线百分比(floor percentage)参数记为f,0 在时点tj,j=1,2,…,n上,TIPP策略的价值底线为 (7) TIPP策略的缓冲额,C(tj),为投资组合市值A(tj)与价值底线F(tj)之差④当A(t)F(t),所有资金均投资于无风险资产。,即 (10) 其中,I{}为示性函数(indicator function),那么该策略称为无借款限制离散时间TIPP策略。 (12) 其中,b>0为杠杆比率(leverage ratio)参数,I{}为示性函数,那么该策略称为借款限制离散时间TIPP策略。 据作者所知,还未有文献以解析形式对有无借款限制下的TIPP策略进行区分。不难验证,上文定义1与定义2所给出的离散时间TIPP策略均满足自融资性质。 1.3收益保证定价 根据1.2节的设定,到期时TIPP策略收益保证的支付(payoff)为max{G-A(T),0}。从支付的形式不难看出,TIPP策略收益保证等价于一个欧式看跌期权。但由于TIPP策略投资组合过程具有路径依赖性(path-dependency),该看跌期权并非普通欧式期权。由风险中性定价理论,该收益保证的价格为 价值底线的设定方式以及借款限制使得TIPP策略投资组合模型形式较为复杂,这使得我们无法得到收益保证价格的解析解,我们将在第2部分采用数值算例来揭示模型参数的变动对收益保证价格的影响。出于示例目的,我们对上述定价问题进行简化以便给出一个封闭形式定价公式。为此我们假定调整时间格栅是等时间间隔的,即ti-ti-1=,i=1,2,…,n,并且=T,这意味着在0时刻按照TIPP策略建立投资组合后便不再调整直至到期。命题1与命题2分别给出了有无借款限制下收益保证的定价公式。 命题1TIPP策略的乘数为m,底部百分比参数为f,初始资金为A(0)=A0,收益保证水平为G,投资期限为T。假定不存在借款限制,且0时刻按照TIPP策略建立投资组合后便不再进行调整。那么GBM与有限跳跃Levy过程情形下收益保证的定价公式分别为 (15) (16) 将(16)代入(13)进行整理可得 当风险资产价格服从GBM过程时,即风险资产价格由(3)、(4)进行刻画时,运用Black-Scholes期权定价公式以及期权平价关系可得收益保证的价格为 当风险资产价格服从有限跳跃Levy过程时,即风险资产价格由(3)、(5)进行刻画时, 运用期权平价关系及Shreve[18]中Theorem11.7.5可得收益保证的价格为 命题2 TIPP策略的乘数为m,底部百分比参数为f,初始资金为A(0)=A0,收益保证水平为G,投资期限为T。假定存在借款限制,杠杆比率b=1,且0时刻按照TIPP策略建立投资组合后便不再进行调整⑥杠杆比率b=1表明投资组合在风险资产上的配置比重不能超出其资金总量。假定b=1并不失一般性,具体论证可参见Black和Perold[3]。。那么GBM与有限跳跃Levy过程情形下收益保证的定价公式分别为 (21) 证明:(i) 与命题1的证明相同。 将(22)代入(13)并化简可得 (23) 由于投资组合模型的复杂形式,我们无法得到收益保证封闭形式的定价公式。本部分通过数值算例来揭示模型参数的变动对收益保证价格的影响。为了便于分析,假定调整时间格栅是等时间间隔的,即ti-ti-1=,i=1,2,…,n。为了模拟S(t)的路径,首先必须得对跳跃幅度的概率分布做出假定。由Kou[14]引入的DEJD过程可解释经验研究中广泛存在的资产日收益的非对称尖峰厚尾特征与期权定价中的波动率微笑(volatility smile)现象,该过程广泛应用于连续时间条件下的金融市场研究。本部分便采用DEJD过程来对风险资产的价格过程进行模拟。回顾(5)式可知,K为价格跳跃幅度,令Y=log(K)。DEJD过程下Y服从双指数分布,其概率密度函数为 表1 模拟参数值的设定 2.1收益保证价格与策略乘数 图1 收益保证价格与乘数关系图 图1报告了TIPP策略收益保证的价格(C)与策略乘数(m)之间的关系。从图1不难看出,离散交易条件下,(1) TIPP策略收益保证存在缺口风险,收益保证的价格大于0且随着策略乘数的增大而增加;(2) 价格跳跃情形下的收益保证价格要高于传统连续价格路径下的收益保证价格;(3) 借款限制使得收益保证的价格下降,且策略乘数越大该效应越显著。本部分的数值算例表明,即便风险资产价格路径是连续的,如果不能连续交易,那么TIPP策略总是存在缺口风险。再者,当风险资产价格存在跳跃条件下,风险资产价格的向下跳跃风险使得TIPP策略投资组合在投资期内更可能跌破策略价值底线,策略的缺口风险上升,收益保证的价格也会相应上升。当策略乘数越大时,TIPP策略投资组合配置在风险资产上的比重也就越大,TIPP策略变得更为激进(aggressive),离散交易所引致的投资组合不能有效地应对风险资产价格下行风险的效应也就越突出,收益保证的缺口风险越严重,收益保证的价格也就越高。 2.2收益保证价格与收益保证水平 图2收益保证价格与收益保证水平关系图 图2给出了收益保证水平(G)对TIPP策略收益保证价格(C)的影响。图2的结果表明,(1) 无论是否存在价格跳跃及借款限制,TIPP策略收益保证的价格皆随着收益保证水平的上升而上升,且二者呈凸函数关系;(2) 同等收益保证水平下,当风险资产价格存在跳跃条件下,TIPP策略收益保证的价格更高;(3) 无论是否存在价格跳跃,借款限制会降低收益保证的价格,且收益保证水平越高该效应越显著。以上几点不难理解:收益保证水平设定的越高,风险资产价格的向下波动风险所引致缺口风险的可能性越高,收益保证的价格就越高。且风险资产价格存在向下跳跃时,相同的风险资产持有量所面临的价格下行风险上升,投资组合的缺口风险也相应上升,收益保证的价格也就更高。而借款限制则通过限制风险资产的最大持有量而对缺口风险进行限制,从而降低了收益保证的价格。 2.3收益保证价格与价值底线百分比 图3报告了TIPP策略收益保证价格(C)与价值底线百分比(f)之间的关系。从图3可以看出,(1)无论是否存在价格跳跃及借款限制,TIPP策略收益保证价格与价值底线百分比之间存在负相关关系;(2)不论是否存在价格跳跃,借款限制降低了收益保证的价格,且价值底线百分比越低,该效应越显著;(3)无论是否存在借款限制,价格跳跃因素提升了收益保证的价格,且价值底线百分比越低,该效应越显著。价值底线百分比越低,TIPP策略配置在无风险资产上的资金比重就越低,配置在风险资产上的比重就越高,不利价格波动所引致的缺口风险就越显著,收益保证的价格就越高。当风险资产价格存在向下跳跃时,价值底线百分比对缺口风险的影响就越强;而存在借款限制时,价值底线百分比对于缺口风险的影响就越弱。 图3 收益保证价格与价值底线百分比关系图 2.4收益保证成本与杠杆比率 图4 收益保证价格与杠杆比率关系图 图4给出了杠杆比率(b)的变动对TIPP策略收益保证价格(C)的影响。图4的结果表明,(1)无论是否存在价格跳跃,TIPP策略收益保证价格与杠杆比率呈正相关关系,且收益保证的价格随着杠杆比率的提高而缓慢增加;(2)风险资产价格存在跳跃条件下的收益保证价格要高于连续路径条件下的情形,且二者之间的差距随着杠杆比率的上升而上升。杠杆比率越大,TIPP策略就越激进,投资组合对于不利波动的风险敞口就越大,收益保证的缺口风险就越严重,收益保证的价格就越高。随着价格跳跃因素的引入,杠杆比率对于缺口风险的放大作用就更加显著。 2.5收益保证成本与调整周期 图5收益保证价格与调整周期关系图 将价格跳跃因素与借款限制因素考虑在内,本文在离散交易框架下对TIPP策略收益保证的定价问题进行了考察。由于TIPP策略投资组合过程的复杂性,我们无法得到收益保证封闭形式的定价公式。文章通过数值算例考察了策略乘数m、收益保证水平参数G、价值底线百分比参数f、杠杆比率参数b,以及调整周期参数,的变动对收益保证价格的影响。数值分析的结果表明:离散交易条件下,(1) 无论是否存在价格跳跃及借款限制, TIPP策略收益保证均存在缺口风险,收益保证的价格大于0;(2) 价格跳跃条件下TIPP策略收益保证价格要高于传统连续价格路径情形;(3) TIPP策略收益保证的价格与策略乘数、收益保证水平、杠杆比率以及调整周期正相关,与价值底线百分比负相关;(4) 借款限制会降低TIPP策略收益保证的价格,且该效应随着策略乘数、收益保证水平、杠杆比率以及调整周期的增加而增强,随着价值底线百分比的提高而减弱。本文的研究可以为TIPP策略收益保证产品市场提供定价基准。此外,本文的研究结果还具有以下两方面含义:(1) 传统GBM假定下的定价研究会低估收益保证的价格,因而会对为收益保证进行担保的第三方机构的利益造成损害;(2) 收益保证类金融产品的发行方与管理方可选取合适的策略乘数、杠杆比率以及价值底线百分比参数来控制保本费率并以此来增强产品的吸引力。 [1] Perold, A F. Constant proportion portfolio insurance[R]. Boston: Harvard Business School, 1986. [2] Black, F, Jones R C. Simplifying portfolio insurance[J]. Journal of Portfolio Management, 1987, 14(1):48--51. [3] Black, F, Perold, A F. Theory of constant proportion portfolio insurance[J]. Journal of Economic Dynamics and Control, 1992, 16(3-4):403-426. [4] Estep, T, Kritzman, M. TIPP: Insurance without complexity[J]. Journal of Portfolio Management, 1988, 14(4):38-42 [5] Bertrand P, Prigent J L. Portfolio insurance: the extreme value approach to the CPPI method[J]. Finance, 2002, 23(2):69-86. [6] Cont R, Tankov P. Constant proportion portfolio insurance in the presence of jumps in asset prices[J]. Mathematical Finance, 2009, 19(3):379-401. [7] Hamidi B, Jurczenko E, Maillet B. A CAViaR Modelling for a Simple Time-Varying Proportion Portfolio Insurance Strategy[J]. Bankers, Markets & Investors, 2009, 5, 4-21. [8] Balder S, Brandl M, Mahayni A. Effectiveness of CPPI strategies under discrete-time trading[J]. Journal of Economic Dynamics and Control, 2009, 33:204-220. [9] Paulot L, Lacroze X. Efficient Pricing of CPPI Using Markov Operators[R]. SSRN eLibrary, 2009. [10] Paulot L, Lacroze X. One-Dimensional Pricing of CPPI[J], Applied Mathematical Finance, 2011, 18(3):207-225. [11] 王亦奇,刘海龙.结合资产配置策略测算多期收益保证价值[J].管理科学学报,2011,14(11):42-51+62. [12] Vasicek, O. An equilibrium characterization of the term structure[J]. Journal of Financial Economics, 1977, 5(2):177-188. [13] Merton, R C. Option pricing when underlying stock returns are discontinuous[J]. Journal of Financial Economics, 1976, 3(1):125-144. [14] Kou, S G. A Jump-Diffusion Model for Option Pricing[J]. Management Science, 2002, 48(8):1086-1101. [15] Sato, K. Levy processes and infinitely divisible distributions[M]. Cambridge university press, 1999. [16] Cont, R, Tankov, P. Financial modeling with jump processes[M]. Chapman & Hall/CRC, 2003. [17] Protter, P E. Stochastic integration and differential equations[M]. Springer Verlag, 2004. [18] Shreve, S E. Stochastic calculus for finance II: continuous-time models[M]. Springer Verlag, 2004. [19] Glasserman, P. Monte Carlo Methods in Financial Engineering[M]. Springer Verlag, 2004. Pricing of TIPP-managed rate of return guarantees under discrete-time trading ZHANG Fei, LIU Hai-long (Antai College of Economics and Management, Shanghai Jiao Tong University, Shanghai 200052, China) Constant proportion portfolio insurance (CPPI) strategy is a dynamic investment technique that aims to protect the underlying portfolio and retain some upside potential. The great applicability of CPPI strategy gains popularity among investors, especially institutional investors. Despite its simplicity, tractability and flexibility, CPPI strategy focuses on securing the principal and fails to protect the interest and profit generated during the course. Time-invariant portfolio protection (TIPP) strategy, as a variant of CPPI strategy, specifies that the floor should be ratcheted up as the market price rises and should retain the previous floor as the market price declines. If there are no jumps in asset price and trading without transaction costs, there is no risk of going below the pre-specified floor while employing CPPI strategy or TIPP strategy to manage the underlying portfolios. In another word, there is no gap risk. However, when asset price dose exhibit that discontinuous moves (jumps) or continuous trading is infeasible because of illiquidity or transaction costs, there is a gap risk with CPPI- and TIPP-managed portfolios. In the presence of gap risk, the issuers of the rate of return guaranteed products must turn to third parties for guarantee or reinsurance. How to figure out a proper reinsurance rate or a proper reinsurance fee is an important practical issue. Although several papers have investigated the valuation of CPPI-managed rate of return guaranteed products, there is no paper exploring the valuation of the TIPP-managed rate of return guaranteed products. This paper aims to fill this gap and investigates the pricing of TIPP-managed rate of return guaranteed products. Since our paper takes into consideration the effect of jumps in asset price, discrete rebalancing and borrowing constraints, our research findings have great practical importance. Specifically, this study employs geometric Brownian motion and finite-activity Levy process to characterize the price process of the active asset and investigates the valuation of the TIPP-managed rate of return guarantees under the framework of discrete rebalancing. Because of the complexity of the TIPP-managed portfolio, closed form pricing formulas cannot be obtained. For illustrative purposes, closed form pricing formulas are given for a special case of TIPP strategy. Our numerical results indicate that under the framework of discrete rebalancing, (1) there is a gap risk with the TIPP-managed portfolio and the price of the rate of return guarantee is positive, irrespective of the presence or absence of jumps in active asset price and borrowing constraints; (2) the price of the rate of return guarantee in the presence of jumps in active asset price is higher than its counterpart under the traditional assumption of continuous sample path of asset price; (3) the price of the rate of return guarantee is positively correlated with the multiple, the guarantee level, the leverage ratio and the rebalancing period, but negatively correlated with the floor percentage; (4) borrowing constraints can decrease the price of the rate of return guarantee and exercise more influence with bigger multiple, higher guarantee level, higher leverage ratio, longer rebalancing period but lower floor percentage. This study can provide a benchmark for the valuation of TIPP-managed rate of return guaranteed products. Moreover, the study has the following two practical implications: (1) valuation under the traditional assumption of geometric Brownian motion underestimates the costs of rate of return guarantees and thus hurts the interests of the third parties who insure the guarantees; (2) the issuers or managers of the rate of return guaranteed products can properly choose the multiple, the leverage ratio and the floor percentage to keep insurance fees under control, thereby enhancing the attractiveness of their products. discrete-time trading; time-invariant portfolio protection (TIPP) strategy; finite-activity Levy process; rate of return guarantee; gap risk 中文编辑:杜 健;英文编辑:Charlie C. Chen F830.59 A 1004-6062(2016)01-0185-06 10.13587/j.cnki.jieem.2016.01.023 2013-08-23 2013-12-08 国家自然科学基金资助项目(71273169) 张飞(1983—),男,河南开封人。上海交通大学安泰经济与管理学院博士研究生,研究方向:金融工程。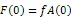
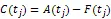
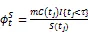
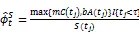
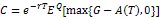
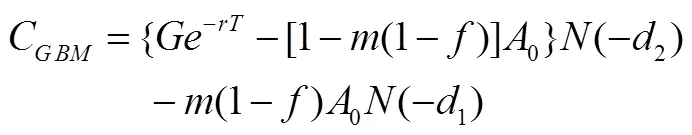
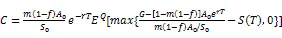
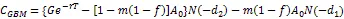
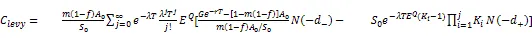
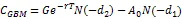
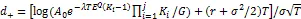

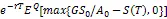
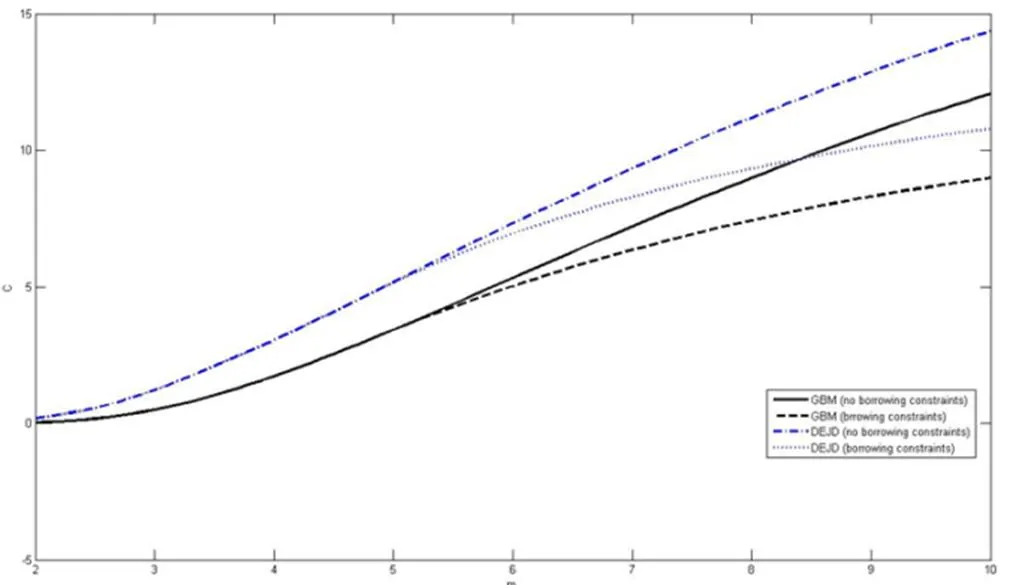
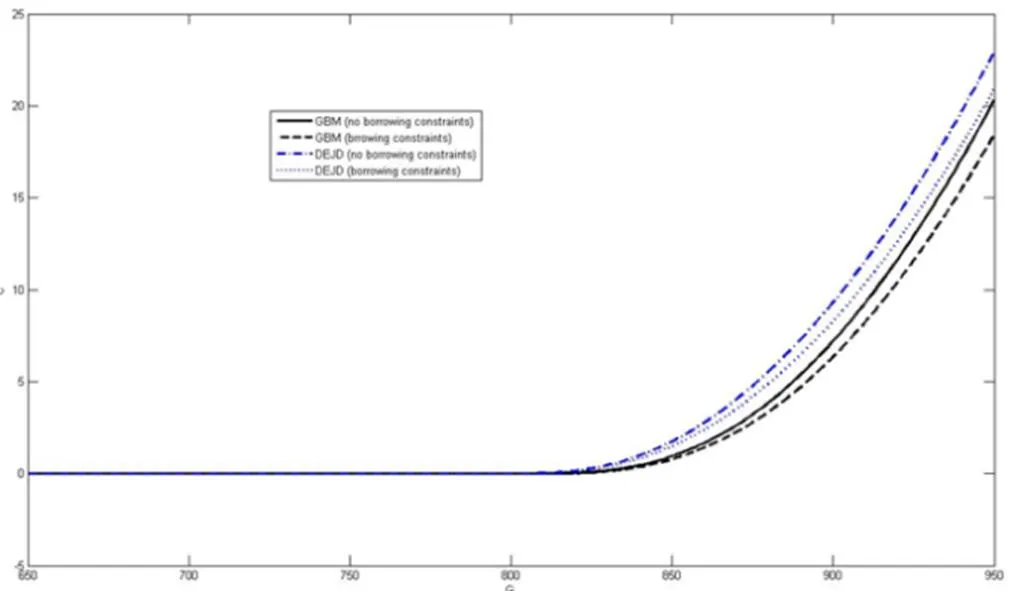
2 数值分析




3 结论
