基于DFD的再制造系统生产及定价联合决策研究

曹晓刚，郑本荣，闻 卉



基于DFD的再制造系统生产及定价联合决策研究

曹晓刚1，郑本荣1，闻 卉2

（1.武汉纺织大学管理学院，湖北武汉430073；2.湖北工业大学理学院，湖北武汉430068）

从产品的可拆卸性设计理论（DFD, Design for Disassembly）及消费者选择偏好理论出发，在消费者对新产品和再制造产品存在异质性偏好的背景下构建了再制造系统利润最大化的两周期带约束生产-定价联合决策模型，探讨了再制造受回收数量约束与不受约束两种情形下系统的最优生产及定价策略，并全面分析了模型中关键参数（消费者偏好、再制造成本节约、产品的可拆卸程度等）变化对均衡价格、产量、系统成员利润和再制造商市场进入决策的影响。研究结果表明：对于制造商来说，考虑产品的可拆卸性战略始终是占优策略，并且在一定的条件下能够有效地阻止再制造商的进入。

可拆卸性设计；再制造；异质性市场；生产策略；定价策略

0 引言

近年来，在经济、社会和环境价值的多重驱动下，废旧产品的回收、再制造逐渐被一些企业所关注并积极运用于实践当中，如HP、SONY、联想和Walmart等。McConocha和Speh[1]研究指出对回收品的再制造不仅能够节省原材料、能源和劳动力成本，减少废旧品对环境的污染；而且能够拓宽企业的产品线，增加市场占有率和提高企业的品牌形象。在我国，一方面经济的迅速发展导致了废弃物的急剧增加，同时消费者对再制造产品的需求也不断在扩大；但另一方面由于我国再制造行业起步较晚，相关的理论基础和实践经验都特别缺乏。鉴于此，对再制造相关问题的研究亟需全面开展。

拆卸性设计是绿色设计的重要组成部分，其基本内涵是指针对制造业生产的缺点把可持续发展思想融入到产品设计的过程中，将保护生态环境与经济发展有机的结合在一起，在保证产品质量的前提下，兼顾环境的要求。产品的可拆卸性是指产品的零部件可以拆分的模块化程度[2]，其直接关系到再制造企业回收和处理废旧产品的技术难度和成本，高可拆卸性的设计不仅大大降低了回收产品的拆卸难度，而且能节省更多的再制造成本；但另一方面也给原始制造商的市场和获利能力带来了较大的冲击。根据Gartner 咨询公司提供的数据资料，2009年全球的打印机墨盒行业由于低价格的再制造产品的冲击所造成的损失超过130亿美元[3]。因此，制造商如何通过确定产品的可拆卸性程度而有效地阻止再制造产品的市场渗透和挤兑，双方战略选择与博弈问题的分析非常具有现实意义，值得深入研究。

关于再制造产品的定价问题，Majumder和Groenevelt[4]，Atasu等[5]，Ferrer和Swaminathan[6]等均在新产品和再制造产品无差异的条件下做了相关的研究。而另一方面随着实践的发展与研究的不断深入，一些学者开始关注再制造产品与新产品价格差异下再制造系统的决策问题。但斌和丁雪峰[7]研究了企业的再制造受回收率约束和不受回收率约束两种情形下再制造产品的最优定价策略，并进一步分析了再制造产品对新产品的市场挤兑与增长效应。谢家平、王爽[9]在Ferrer和Swaminathan[8]研究的基础上，探讨了偏好市场下制造/再制造系统的最优价格及产量决策。大部分的研究都指出再制造商的进入会蚕食部分新产品的市场并降低制造商的盈利能力，因此，制造商的战略选择与再制造商市场进入条件的相互关系问题逐渐引起了人们的关注。Ferguson和Toktay[10]，李帮义[11]研究了寡头垄断和竞争条件下再制造系统的最优定价策略，并指出垄断者可以采取恐吓的手段阻止再制造商进入市场。Debo等[12]建立了再制造产品和新产品分别定价并通过技术选择影响再制造水平的单周期和多周期利润最大化模型，指出制造商不同的技术选择会影响到再制造商的决策结构与市场格局。可以看出，上述文献大都从成本节约与消费者偏好的角度研究了再制造产品与新产品的定价决策，关于制造商的产品设计决策和再制造商生产与定价策略的相互关系的研究，Kim和Chhajed[13]指出在产品的设计阶段考虑可拆卸性能节约制造和装配成本，并且有利于规模经济的实现。Desai[14]通过研究发现制造商的生产成本在很大程度上取决于企业的产品设计战略和市场战略，如产品的可拆卸性。而具体到产品的可拆卸性决策来看，Ijomah等[15]指出低可拆卸性的设计会大大增加再制造的难度和成本。Teunter[16]应用随机动态规划的方法，建立了产品的拆卸-回收决策模型，讨论了企业进行再制造的条件。Hua等[17]将市场细分为高端和低端市场，建立了两阶段的Stakelberg动态博弈模型，分析了制造商的产品设计决策对下游零售商定价策略影响。Wu[18]利用博弈论的方法构建了再制造系统的最优价格-产量决策模型，考虑了制造商产品设计决策的影响，得到了双方价格和产量决策的最优均衡解，并将模型扩展至多周期和无限期情形。

总体来看，目前关于再制造系统决策问题的研究更多的是论证再制造在经济上和营销上的理论意义和现实意义，而在竞争的视角下关于制造商与再制造商最优策略的选择及相互关系的研究却很少涉及。关于产品可拆卸性设计的研究大多数都只关注一些特定的问题，如提高质量、节约成本或者是废旧产品的回收再利用等，而很少涉及到拆卸策略对再制造系统定价决策影响。本文在文献[18]研究的基础上，引入可拆卸性设计理论和消费者选择偏好理论，选取单一制造商和再制造商进行研究。在此基础上，在双周期环境下探讨制造商的拆卸决策对双方定价和产量决策的影响，并分析再制造商进入市场的条件。

1 问题描述和模型假设

研究了一个由原始制造商和再制造商构成的双寡头垄断竞争的再制造系统。制造商负责新产品的生产，单位生产成本为；再制造商负责废旧产品的回收及再制造，单位生产成本为，其中，表示生产每单位的再制造产品所带来的再制造成本节约。假设消费者对再制造产品的价值评价低于新产品[5-8]，即对新产品的价值评价为1，对再制造产品的价值评价是新产品的折扣。考虑两周期的决策情形，且每期潜在的市场容量均设为，第一阶段，制造商对新产品的可拆卸程度及价格进行决策，并将产品销售至消费市场；再制造商在第一阶段末对对市场中的废旧产品进行回收，设回收率为，然后进行再制造产品的生产并将产品投入到市场与制造商展开竞争。

根据消费者的效用关系，第一阶段消费者购买新产品的效用函数为，所以此阶段的市场需求函数满足关系式。第二阶段，再制造产品进入市场与新产品展开竞争，设此阶段新产品和再制造产品的价格分别为和，二者满足。我们采用Hottelling价格竞争博弈模型来刻画制造商和再制造商竞争情形下的需求函数[19]。假设一个消费者最多只购买1单位的产品，表示再制造商与消费市场之间的距离，表示制造商到消费市场的距离，。消费者购买产品所产生的单位“旅行成本”为，值越大表示两种产品之间的差异性就越大。所以可由此得到位于处的消费者购买新产品和再制造产品的效用分别为，。消费者根据效用最大化的原则确定购买哪一种产品，当满足且时，消费者会选择购买新产品；反之则购买再制造产品。则第二阶段新产品及再制造产品的需求函数如下

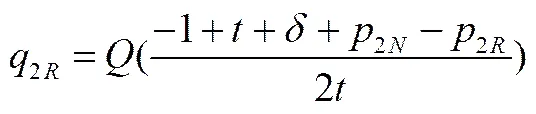
此外为了便于分析，对模型作如下假设。（1）外部市场及成员内部之间的信息是完全对称的，即制造商和再制造商均可利用对彼此最优决策的反应函数确定自己的最优战略。其次，制造商和再制造商均为风险中性决策者，且均基于利润最大化的目标进行决策。（2）根据文献[17,18]的研究，假设所有的产品均只能回收再制造一次，从而确保了不同阶段消费者购买决策的独立性。（3）再制造系统中，制造商为Stackelberg博弈的领导者，再制造商为跟随者。

2 基准模型及求解

由上文描述可知，制造商和再制造之间是一种序贯博弈结构。具体的决策顺序为：制造商在第一阶段首先确定新产品的最优拆卸水平以及新产品的最优销售价格；然后，制造商和再制造商在第二阶段的决策中同时确定产品的最优销售价格和。根据Ferrer和 Swaminathan[8]文中的假设，制造商在第一阶段根据企业的生产计划确定新产品拆卸水平和价格决策，可以看做是企业的一项常规决策。因此可看出，双方之间是完全信息下的动态博弈，其均衡是子博弈精炼纳什均衡，则制造商基于利润最大化的生产-定价决策模型如下：

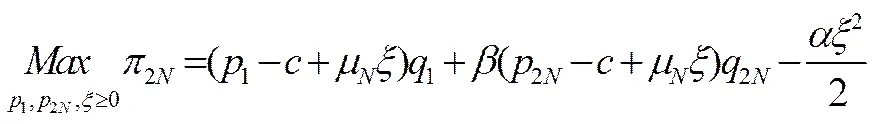
上式中第一项和第二项分别表示制造商在第一阶段和第二阶段销售产品所带来的利润，第三项表示制造商考虑产品的可拆性设计战略而产生的固定成本。在第一阶段末期，再制造商从市场中回收废旧产品并进行再制造。根据假设及现实的经济规律，再制造商很难完成对所有废旧品的回收，我们假设再制造商最多回收数量的废旧品，那么再制造商基于利润最大化的生产-定价决策模型为

（4）

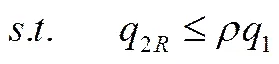
不等式（5）是表示再制造商回收数量的约束。运用逆向归纳法对模型进行求解，对于再制造商的利润函数，容易看出有，所以目标函数是严格的凹函数；另外约束条件（5）具有凸函数的性质。因此，再制造商的决策模型是一个凸规划问题，存在唯一的最优解。构造以下拉格朗日函数

（6）

根据一阶K-T条件并联立方程组，我们首先可得到第二阶段新产品和再制造产品价格关于制造商第一阶段拆卸水平和价格的最优反应函数。

命题1表明存在一个回收率阈值使再制造生产决策是否受约束，其中阈值是关于制造商第一阶段产品价格和拆卸程度的函数，说明双方均在第一阶段决策的基础上选择最优反应函数。根据命题1可以求出制造商第一阶段决策的最优解，我们用和分别表示再制造生产决策不受约束与受约束两种情形下的最优解。根据命题1，当时，表示再制造生产不受回收量约束，易得制造商第一阶段的决策最优解如下

（8）

（10）

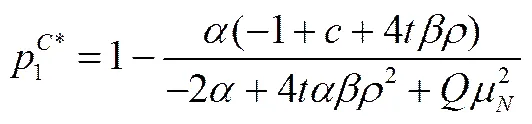
（12）

（13）

命题2如果上述均衡解均满足非负性，则满足第二阶段最优价格的条件下制造商的目标函数是关于和的联合凹函数。

对应的行列式

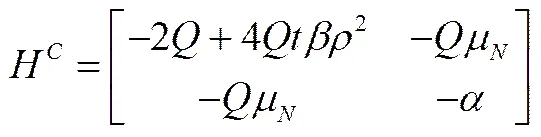
命题2保证了所建模型存在唯一的最优解使得制造商和再制造商的利润实现最大化，因此，将第一阶段的均衡解带入到双方的利润函数中，从而获得第二阶段再制造系统的最优化决策。

命题3给出了制造商采取不同拆卸策略的条件。再制造不受回收数量约束条件下，当制造商提高产品的拆卸程度所带来的成本节约超过一定的值时，高可拆卸性策略对制造商来说会更为有利；而当足够小时，制造商会通过选择低可拆卸战略以降低再制造商的成本优势。而当再制造受回收数量约束条件下，与无关，此时所有回收的产品均都用于了再制造，再制造产品的价格与再制造成本节约参数和无关，因此新产品与再制造产品在市场上不直接的进行价格竞争，制造商的拆卸决策对再制造产品的定价不产生直接的作用，从而制造商为了获得更多利润会提高产品的可拆卸性程度。

3 再制造系统均衡决策分析

根据上一部分所求得的均衡解，本节将分析模型中一些关键参数对均衡价格和产量的影响；并进一步探讨再制造商进入市场的边界条件。

命题4表明，若再制造不受回收数量约束，当拆卸战略给制造商带来的成本节约高于给再制造商带来的成本节约时，再制造成本节约越大，制造商相应地会提高第一阶段新产品的价格并且降低产品的拆卸水平以阻止再制造商的竞争，从而增加单位产品的边际利润。第二阶段，若再制造成本节约提高，再制造商会选择降低再制造品的销售价格，从而销售量增加，企业的利润也因此上升；而同时制造商为了在与再制造商竞争的过程中获取更多的优势，不得不降低产品的销售价格。当再制造受回收数量约束时，由命题可知新产品与再制造品之间不进行直接的价格竞争，制造商的决策不受再制造成本节约的影响，因此，再制造成本节约越高，再制造商所获利润也就更多。

从命题5可以看出，消费者价值折扣与再制造成本节约对均衡解的影响较为相似。再制造数量决策不受约束时，再制造产品的价格与产量均随价值折扣的增加而增加，说明了消费者对再制造品的价值折扣越高，对再制造商也就会越有利。但消费者的价值折扣越高，双方的价格竞争在一定程度上会损害制造商的利益，因此制造商会相应的调整第一阶段的拆卸和定价决策应对竞争。再制造数量决策受约束时，价值折扣越高，再制造商为了获取更高的利润也会随之采取高价策略，其他的决策不受价值折扣系数的影响。

命题6再制造决策不受回收数量约束时，再制造商进入市场的边界条件为

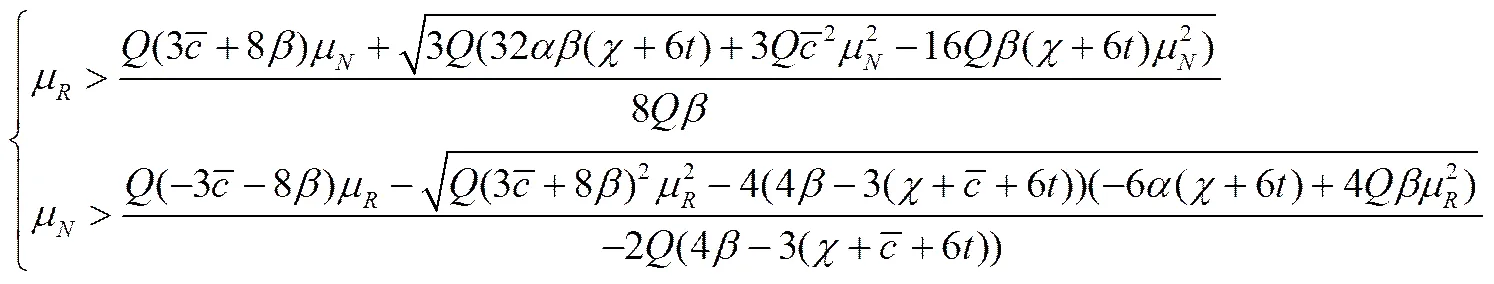
而当再制造受回收数量约束时，再制造商进入市场的边界条件是：。

从命题6可以看出，再制造不受回收数量约束时，再制造商进入市场的成本阈值关于市场容量是递减的，市场规模越大，再制造商进入市场的条件也就越高，这是因为市场规模足够大时，制造商可以使用低可拆卸性战略或者不考虑产品的可拆卸性策略，从而使再制造商盈利的空间变小。另外，成本节约与的差值越来越小时，制造商的拆卸战略对于阻止再制造商的进入与挤兑的作用逐渐减小直至无效。当再制造受回收数量约束时，再制造商进入市场的阈值关于回收率是递减的，说明回收率越高，再制造商进入市场的阻碍就会越小。

4 算例分析

为了更好地了解模型中关键参数变化对制造商和再制造商最优决策及均衡利润的影响，探究文中模型的理论分析难以得到的一些性质，进一步发掘其实践和管理意义，下面进行数据的仿真分析。本节内容主要分为以下三个部分：1）分析再制造成本节约与消费者对再制造产品的价值折扣系数对均衡产量与利润的影响；2）分析制造商的拆卸战略选择对再制造系统成员利润的影响；3）进一步利用得益矩阵的方法分析制造商与再制造商的战略选择过程及寻找此博弈的纳什均衡。取初始数据如下：，，，。

4.1成本节约和价值折扣对均衡产量和利润的影响分析

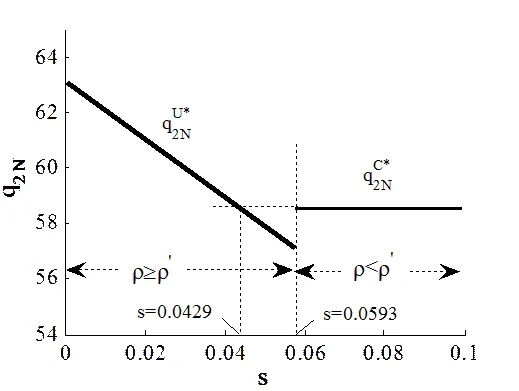
图1 均衡产量随再制造成本节约变化情况

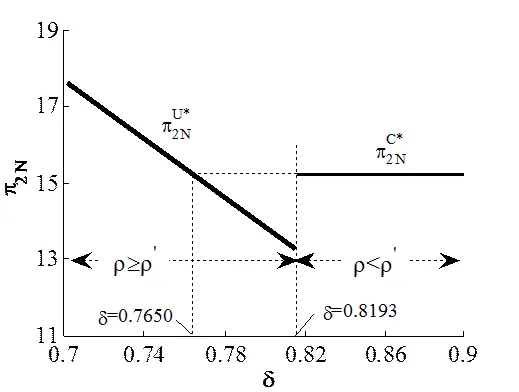
图2 均衡利润随消费者价值折扣系数的变化情况

图1表明：当再制造不受回收数量约束时，再制造商的产量随着再制造成本节约的增加而增加，但制造商的产量随着再制造成本节约的提高却不断减少。当再制造成本节约满足的条件时，再制造受回收数量约束，此时双方的产量决策不受再制造成本节约影响的变化，因此保持在同一水平上。通过对比可以发现，再制造成本节约的上升有利于再制造商，但并不总是一定会伤害制造商的利益（），这是因为当再制造成本节约不断增加直至超过一定的阈值时，此时制造商的决策不再直接受到再制造商的影响。

从图2可以看出：消费者价值折扣系数对于双方均衡利润的影响与图3所说明的结论是一致的。时，再制造不受回收数量约束，此时消费者价值折扣越高，再制造商的利润就不断地增加，而制造商的利润则成下降趋势。再制造受回收数量束时，由于双方不展开直接的价格竞争，因此制造商的利润不受价值折扣的影响，说明了鼓励消费者购买再制造产品能使再制造商获得更多的利润。此外，我们发现再制造受回收数量约束的情形对于制造商来说并不总是不利的，当时，再制造商更愿意回收部分产品进行再制造，而当时，此种情形对于制造商来说也更为有利。

4.2 制造商拆卸战略选择对均衡利润的影响分析

Remanufacturing is unbound ()

Remanufacturing is bound ()

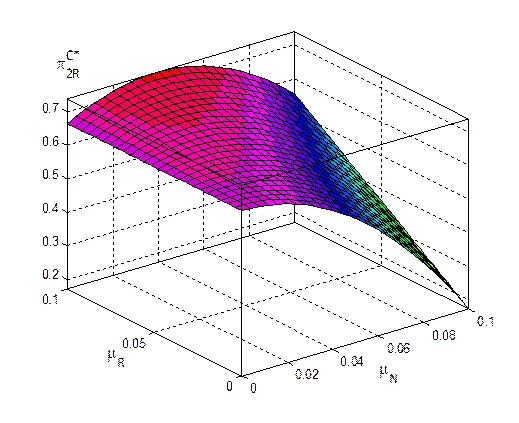
图3 成本参数和对均衡利润的影响分析

图3反映了制造商的拆卸决策对决策双方均衡利润的影响。再制造不受回收数量约束情形，我们可以看到当成本节约与的差值越来越小时，再制造商相应能获得更多的利润。这是因为当差值越来越小时，制造商的拆卸决策在阻止再制造商进入市场和再制造产品的挤兑时的作用被抵消，所以此种情形下制造商的拆卸战略不能有效的阻止再制造商的进入与挤兑。而制造商的利润水平受的影响则比较大，而基本上与的变化无关，当拆卸决策给再制造商带来的成本的节约逐渐增加时，我们发现制造商的利润是不断下降的，这充分说明了制造商考虑拆卸决策的重要性。再制造受回收数量约束时，制造商所获利润与无关，关于递增，这与命题3的结论是一致的。再制造商的利润受的影响较大，而基本上不再受变化的影响；同时，当与越来越接近时，再制造商相应能获得更多的利润，而此时制造商的拆卸策略对再制造商市场进入的阻止作用也会逐渐减小，符合命题6的结论。

4.3 再制造系统生产-定价策略博弈分析

为了进一步分析制造商和再制造商的战略选择与博弈过程，我们用和分别代表制造商考虑和不考虑产品的拆卸决策，用和分别表示再制造商选择高回收率策略（再制造不受回收数量约束）和低回收率策略（再制造受回收数量）。选取数据：，，，，，接下来我们将通过一定的数值计算寻找此博弈的纳什均衡。

表1 再制造系统生产—定价博弈的战略式表述

5 结论

本文针对单一制造商和单一再制造商构成的再制造系统，考虑制造商的拆卸性决策与消费者对新产品和再制造产品具有异质偏好，构建了基于利润最大化的两周期带约束生产与定价联合决策模型。通过模型求解发现，存在一个回收率阈值使再制造商生产决策不再受约束，在这两种情形下对比分析了折现率、成本节约、消费者价值折扣系数等参数对双方的均衡价格、产量和利润的影响，得到了再制造商进入市场的条件；并从博弈论的角度研究了制造商领导的Stakelberg博弈，分析了双方的战略选择过程。研究结果表明：产品的可拆卸性决策所引起的双方的成本节约的差值越大时，再制造商进入市场难度就越大，从而制造商的阻止战略就越有效；而无论再制造商的数量决策是否受约束，制造商在设计阶段考虑产品的拆卸决策对于制造商来说始终是占优策略，但并不总是会伤害再制造商的利益。

本文可从以下几方面进行扩展，将文中模型扩展到多周期情形是今后的研究方向之一。此外，本文假设制造商只负责新产品的制造，研究制造商同时从事再制造的决策模型更具现实意义。最后，本文只针对于制造商和再制造商的定价问题进行研究，而新产品和再制造产品的价格和质量竞争的 研究值得进一步去探索。

[1] McConocha D,Speh T.Remarketing: commercialization of remanufacturing technology [J].The Journal of Business and Industrial Marketing, 1991,6:23-37.

[2] Mok H S,Kim H J,Moon K S.Disassemblability of mechanical parts in auto-mobile for recycling [J].Computers and Industrial Engineering, 1997,33(3-4):621-624.

[3] Tripathi V,Weilerstein K,McLellan L.Marketing essentials:what printer OEMs must do to compete against low-cost remanufactured supplies. Gartner Inc.,2009.

[4] Majumder P,Groenevelt H.Competition in remanufacturing [J].Production and Operations Management,2001,10(2):125-141.

[5] Atasu A,Sarvary M,Wassenhove L N.Remanufacturing as a marketing strategy [J].Management Science,2008,54(10): 1731-1746.

[6] Ferrer G,Swaminathan J M.Managing new and remanufactured products [J].Management Science,2006,52(1):15-26.

[7] 但斌,丁雪峰.再制造品最优定价及市场挤兑与市场增长效应分析[J].系统工程理论与实践,2010,30(8),1371-1379.

[8] Ferrer G,Swaminathan J M.Managing new and differentiated remanufactured products [J].Management Science,2010,203(2): 370-379.

[9] 谢家平,王爽.偏好市场下制造/再制造系统最优生产决策[J].管理科学学报,2011,14(3),24-33.

[10] Ferguson M E,Toktay L B.The effect of competition on recovery strategies [J].Production and Operations Management,2006,15(3): 351-368.

[11] 李帮义.作为阻止战略的再制造决策研究[J].控制与决策,2010,25(11):1675-1680.

[12] Debo LG,Toktay L B,Wassenhove L N V.Market segmentation and product technology selection for remanufactured products [J].Management Science,2005,51(8):1193-1025.

[13] Kim K,Chhajed D.Commonality in product design: cost saving, valuation change and cannibalization [J].European Journal of Operational Research 2000,125(3):602-621.

[14] Desai P S.Quality segmentation in spatial markets:when does cannibalization affect product line design?[J].Marketing Science, 2001,20(3):265-283.

[15] Ijomah W L,Mcmahon C A,Hammond G P,.Development of robust design-for-remanufacturing guidelines to further the aims of sustainable development [J].International Journal of Production Research,2007,45(18-19):4513-4536.

[16] Teunter R H.Determining optimal disassembly and recovery strategies [J].Omega,2006,34(6):533-537.

[17] Hua Z,Zhang X,Xu X.Product design strategies in a manufacturer–retailer distribution channel[J].Omega, 2011,39(1): 23-32.

[18] Wu C H.Product-design and pricing strategies with remanufacturing [J].European Journal of Operational Research,2012,222(2): 204-215.

[19] Hotelling H.Stability in competition [J].Economic Journal,1929, 39(153):41-57.

[20] Savaskan R C,Bhat T S,Wassenhove L N V.Closed-loop supply chain models with product manufacturing [J].Management Science,2004,50 (2):239-252.

[21] Savaskan R C,Wassenhove L N V,Reverse channel design:the case of competing retailers [J].Management Science,2006,52(1):1-14.

Joint Decision of Production and Pricing for Remanufacturing System Based on DFD Theory

CAO Xiao-gang1, ZHENG Ben-rong1, WEN Hui2

(1.School of Management, Wuhan Textile University, Wuhan 430073, China; 2. School of Science, Hubei University of Technology, Wuhan 430068, China.)

Recycling and remanufacturing of used products have received increasing concern because of global environmental pollution and energy shortage problems. Product remanufacturing can not only help firms reduce production cost and increase profit, but also place less of a burden on the environment and improve social benefits. As defined in many existing literatures, remanufacturing is the process of restoring used products to a usable condition which meets the demand of consumers who pursue low-priced, environmentally friendly products. In a competitive remanufacturing system, the strategic choices of original equipment manufacturers (OEMs) would produce great effect on remanufacturers’ decision, including collection, pricing strategies and so on. The existing literatures on remanufacturing system are mainly related to the market segmentation between OEMs and remanufacturers. There are limited literatures about the influence of OEM’s product design strategies on the remanufacturer’ pricing decisions.

Design for disassemblability (DFD) has been viewed as an important part of the green design. The disassemblability is considered as a modular degree to which the product can be disassembled without force. High disassemblability, on the one hand, can reduce disassemblability difficulty for the remanufacturer and gain higher cost savings. On the other hand, it would also decrease OEMs’ profitability because of the remanufacturer’ cannibalization effect. Thus, the aims of this research are to examine (1) the interaction between pricing decisions of supply chain members in the remanufacturing system, and (2) the level of disassemblability chosen by the OEMs that affects chain members’ production cost structure.

We consider a remanufacturing system consisting of one manufacturer and one remanufacturer. First, we adopt the game theory to establish a two-period profit-maximizing model. In the model, OEM determines its product disassemblability level in the first period, and then the remanufacturer enters the market to compete with the OEM in the second period. Second, this paper derives the optimal prices and the optimal product disassemblability level for two cases that remanufacturing is unconstrained and remanufacturing is constrained. Third, we further characterize the effect of cost savings, parameters associated with product design, consumers’ preference to remanufactured products on the equilibrium decisions and profits. Fourth, some numerical examples are conducted and some new findings are revealed.

This study shows some interesting insights. First, the remanufacturer is always beneficial from the rising cost savings from remanufacturing; however, it is not always harmful to the manufacturer because the manufacturer’s strategy is independent of the remanufacturer’s decision when certain conditions are satisfied. Second, the product-design strategy is effective in deterring market entry by the remanufacturer when cost changes for new products and remanufactured products are substantial. The OEM’s advantage would gradually decrease when cost changes associated with product design strategy are similar for OEM and remanufacturer. Third, through the analysis of the strategic game between OEM and remanufacturer, we find that adopting the product-design strategy is always the dominant strategy for the manufacturer no matter whether remanufacturing is constrained or not. However, the product-design strategy adopted by the OEM may also be beneficial to the remanufacturer when some certain conditions (the production cost or the remanufacturing cost-savings is sufficient low) are bounded.

DFD theory; remanufacturing; heterogeneous market; production strategy; pricing strategy

中文编辑：杜 健；英文编辑：Charlie C. Chen

F274

A

1004-6062(2016)01-0117-07

10.13587/j.cnki.jieem.2016.01.014

2013-01-15

2013-10-25

国家自然科学基金资助项目(71301126）；教育部人文社会科学研究资助项目（11YJC630011)；湖北省教育厅人文社会科学研究资助项目（2015Y071, 2015Q071）；湖北省高校人文社会科学重点研究基地：企业决策支持研究中心资助项目

曹晓刚（1982—），男，山西高平人，武汉纺织大学副教授，博士，主要从事再制造与闭环供应链的研究。