考虑三维装箱约束的多车场车辆路径问题

颜 瑞，张 群，胡 睿



考虑三维装箱约束的多车场车辆路径问题

颜 瑞1，张 群2，胡 睿2

（1.北京信息科技大学经济管理学院，北京 100192；2.北京科技大学东凌经济管理学院，北京 100083）

针对实际物流配送问题的特点，研究三维装箱约束车辆路径问题，首次建立考虑多车场的三维装箱约束车辆路径问题模型，并提出求解该问题的混合算法。混合算法采用遗传算法求解车辆路径问题，采用引导式局部搜索算法求解三维装箱问题。通过计算标准算例检验算法性能，试验结果表明混合算法能够在较短时间内得到质量较高的近似最优解。通过数值仿真检验模型的可解性。

车辆路径问题；多车场；三维装箱；遗传算法

0引言

车辆路径问题（Vehicle Routing Problem，VRP）和装箱问题（Bin Packing Problem，BPP）都是经典的组合优化问题，且都属于NP-Hard问题。在过去的几十年里，对VRP和BPP的研究都取得了非常丰硕的成果，但是关于这两个问题的研究是独立进行的。然而，现实的物流配送中有很多情况是需要同时考虑“装箱”和“运输”这两个问题的，比如家电、家具的送货上门服务。这类配送问题通常具有相似的特征，比如运输工具是带长方体封闭式车厢的货车，货物通常装在长方体的包装箱内，车辆需要拼装运送不同体积、不同重量的货物。对于这类问题，“装箱”和“运输”这两方面是不可分割、相互制约的，只有同时考虑这两点才能即保证选择的配送路线成本最低，又保证货物可以全部合理地装入车辆。近几年，这类问题开始吸引国内外学者的关注，并且已经取得了一些成果。

Iori于2005年提出了二维装箱约束限制容量车辆路径问题（Two-Dimensional Loading Capacitated Vehicle Routing Problem，2L-CVRP）的模型，并提出启发式算法和精确算法结合的方法进行求解，通过大量的仿真计算检验了问题的可解性和算法的可靠性[1]。2L-CVRP模型提出以后，学者们相继提出了不同的算法对该模型进行求解，改善了Iori最初的求解结果，这其中有分支切割法[2]、禁忌搜索算法[3]、文化基因算法[4]、模拟退火算法[5]以及改进的禁忌搜索算法[6]。在2006年，Iori与Gendreau、Laporte等人合作提出了三维装箱约束限制容量车辆路径问题（Three-Dimensional Loading Capacitated Vehicle Routing Problem，3L-CVRP）的模型，并提出禁忌搜索算法进行求解，根据实际案例设计了几种不同约束下的模型并分别进行求解[7]。随后，Moura和Oliveira针对BPP和CVRP分别设计算法，采用层次方法求解BPP、采用贯序方法引导局部搜索的启发式策略求解CVRP[8]。Fuellerer和Doerner等人采用蚁群算法求解3L-CVRP模型，并根据路径和装箱分别设计了信息素更新策略[9]。2010年，Iori和Martello对CVRP和BPP的研究进行了系统的总结，明确了一些基本概念和基本问题，包括2L-CVRP、3L-CVRP及带装箱约束的装卸一体旅行商问题（Traveling Salesman Problems with Pickup & Delivery and Loading Constraints， TSPPDL）等[10]。3L-CVRP考虑三维空间中的货物和车厢，充分体现了实际物流配送情形，因此本文针对3L-CVRP进行研究。

国内关于CVRP和BPP联合问题的研究成果相对较少。马珊静和陈峰等人研究了一维装箱和车辆路径的联合问题，以最小化仓储成本、运输成本和车辆运营成本总和为目标，提出了三种不同策略的两阶段启发式算法进行求解[11]。宁爱兵和熊小华等人研究了物流配送中的三维装箱问题，考虑到三维装箱和车辆路径相结合的一些基本问题，并提出了一种求解三维装箱问题的算法，但是文献并没有把两个问题联合起来进行建模和求解[12]。王征和胡祥培等人针对易损、易碎物品的运输问题进行研究，建立了较为完整的2L-CVRP数学模型，并提出了求解该模型的一个Memetic算法，算法中设计了一种基于深度优先的装箱问题求解策略，文献采用Iori提出的标准算例进行计算，全面分析了Memetic算法的求解效率、求解性能和鲁棒性，试验取得了较为理想的结果[13]。

目前，对于3L-CVRP的研究均以经典VRP模型为基础，模型中只考虑一个配送中心的情况，这在理论上和实践上存在很多不足。在经典VRP模型的基础之上，已经发展出包括多车场、带时间窗及不确定顾客需求量等诸多因素的VRP模型，而到目前为止3L-CVRP模型尚未建立考虑这些因素的模型，在理论上具有较大的研究空间。现代商业模式对物流业的发展提出很高要求，最根本的要求是快速将货物送达顾客，这需要物流企业具有较强的快速反应能力和系统协调能力，而在一个城市或地区建立多个配送中心是实现这个目标的途径之一。在现代城市物流配送模式（比如电子商务网站的配送模式）中，销售商通常在一个城市中拥有几个配送中心，根据总配送距离最短的原则从不同的配送中心同时发货，在较短的时间内把货物送给客户，从整体上提高配送效率。因此，本文在研究三维装箱约束车辆路径问题的基础之上，考虑多配送中心的情况，建立考虑三维装箱约束多配送中心车辆路径问题（Three-Dimensional Loading Multi-Depots Capacitated Vehicle Routing Problem，3L-MDCVRP）的混合数学模型。由于3L-MDCVRP模型是两个NP-Hard问题的结合问题，因此为了在有效时间内得到问题的最优解，本文提出遗传算法和引导式局部搜索算法相结合的混合算法进行求解。

1模型建立

1.1问题描述

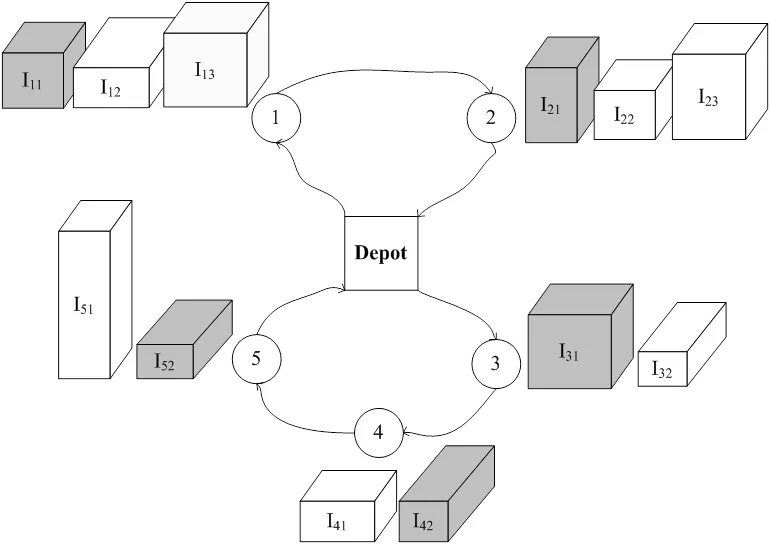
图1 3L-CVRP可行配送方案示意图

3L-CVRP模型假设：

2）每条线路上顾客的货物总重量不能超过车辆最大载重，货物总体积不能超过车厢最大容积，每辆车行驶距离不受限制；

3）每条回路上顾客需求的货物必须全部装入车厢，且满足全部给定的装箱约束；

4）货物从车厢尾部的车门进出，装货过程从车厢内侧左下角开始，假设装货工具可以把货物摆放到车厢内任意位置；

5）以所有车辆的行驶路程之和最小为目标。

在模型假设中，有一个很重要的概念——装箱约束。货物装箱除了要满足车辆限重和车厢限容这两个基本约束条件之外，还应满足符合实际操作的一些约束条件，比如货物不能悬空放置、不能重叠放置以及交通法规限定的其他要求等。装箱约束主要包括：

1）基本约束：货物不能悬空放置、不能重叠放置，货物总重和总装载空间不能超过车辆载重和车厢容积。

2）方向性约束：货物边缘必须与相应的车厢边缘平行，每个货物都是顶部朝上放置，且只能在水平面上做90°的旋转，不能以其它角度或者在垂直面上旋转，可参考图2。

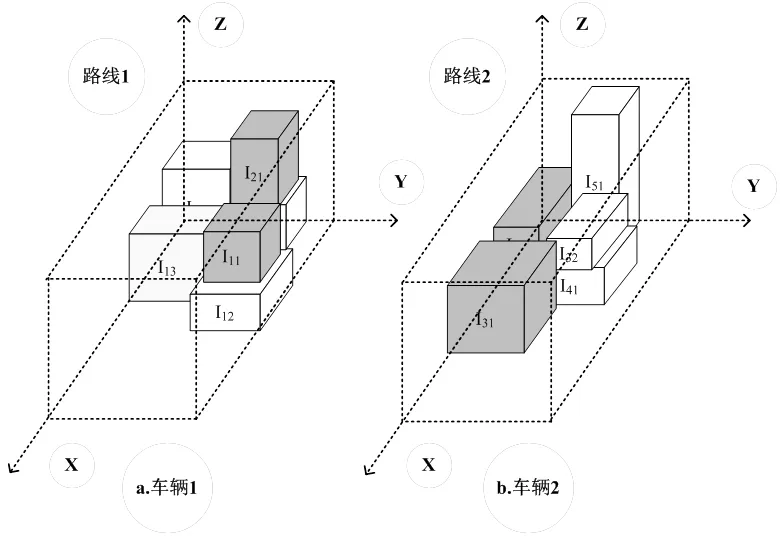
图2 3L-CVRP可行装箱方案示意图

4）LIFO（Last-in-First-out）约束：为了缩短装卸货时间，货物摆放位置需要满足连续装卸货的要求，即先进的货物后出，先出的货物后进。具体描述为，当车辆服务顾客的时候，可以从车尾门方向连续的卸载顾客的所有货物（），且不用挪动其他顾客的货物。根据图1的配送线路，线路1先经过顾客1再经过顾客2，那么在图2.a的装箱图中，就不能出现（）放置于（）上方或者前方的情况。

5）易碎品约束：货物可以分为易碎品和非易碎品。易碎品可以放置在易碎品和非易碎品之上，而非易碎品只能放置在非易碎品之上，即不能出现非易碎品放置在易碎品之上的情况。如图2.a所示，易碎品可以放在易碎品之上。

本文建立的3L-MDCVRP在模型假设上有如下调整：一、有多个配送中心，每个配送中心均存储和供应足够多的产品；二、每个配送中心均有相同数量相同型号的车辆，车辆从配送中心出发完成任务之后返回原配送中心。其他假设和装箱约束均与3L-CVRP一致。

1.2数学模型

本文建立的3L-MDCVRP模型分为车辆路径模型和三维装箱模型两个部分。

在建立模型之前，先给出模型中各个变量的符号和意义，如表1所示。

表1 模型变量及解释

模型中的决策变量为：

建立多配送中心车辆路径模型如下：

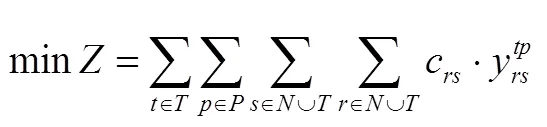
s.t.，，（2）

，，（3）

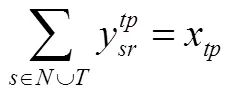
，，，（5）

，，（6）

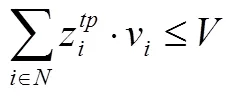
，，，，（8）

，，，

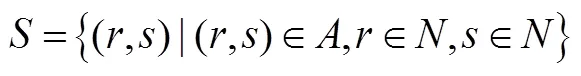
模型解释如下：目标函数（1）表示最小化车辆行驶路程；式（2）表示所有顾客只被访问一次；式（3）和式（4）表示车辆从某个配送中心出发，服务完所有顾客之后返回原配送中心；式（5）表示车辆进入某节点，也必须从该节点离开；式（6）表示每辆车装载货物的重量之和不超过车辆限制载重；式（7）表示每辆车装载货物的体积之和不超过车辆限制容积；式（8）绑定了三维装箱变量和车辆路径变量；式（9）为支路消除约束，保证任何路线中只包含一个配送中心。

在建立三维装箱模型之前，先建立一个笛卡尔坐标系。坐标系的坐标轴分别对应于车厢的长、宽和高，坐标系的原点位于车厢内侧左下角，如图3所示。货物底部左后方的位置（离原点O最近的顶点）用坐标表示，则有：

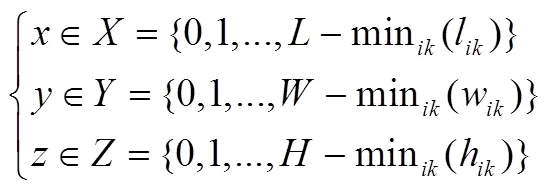
由于货物大小不同，因此即使货物总体积小于车厢容积，也有可能无法将所有货物都装入车厢。考虑到这一点，本文以最大化装入车厢内货物数为目标建立三维装箱模型，则可行解的目标函数值等于总货物数。三维装箱模型如下：

s.t.，

，，（11）

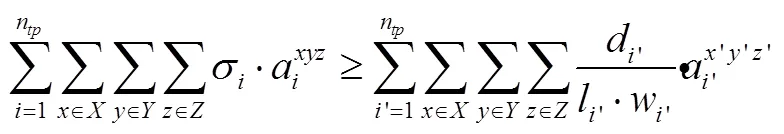
，（12）

，

，

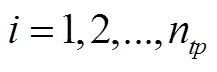
，，（14）

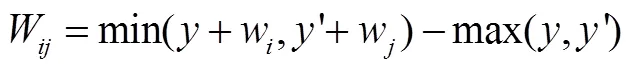
，，（15）

，，（16）

式（10）为目标函数，最大化装入车辆的总货物数；式（11）保证了所有货物都必须有支撑区域（不可悬空放置），且货物不能堆叠；式（12）用以区分易碎品和非易碎品，取值为0表示货物为易碎品，取值为1表示非易碎品，非易碎品不可放在易碎品之上；式（13）给出了决策变量；式（14）和式（15）计算货物的长和宽；式（16）给出每辆车装载货物总数。模型中的变量和标识参考文献[14]和文献[15]。

2算法设计

对于3L-MDCVRP这样的NP-Hard问题，如何在较短的时间内给出有效的解是非常重要的。处理独立的车辆路径问题和三维装箱问题的时候，通常采用启发式算法进行求解，但是两个问题结合起来之后，现有的启发式算法已经无法求解。本文设计3L-MDCVRP求解算法的基本思路为：1）先求出一个最优配送线路，当有了一个配送线路之后，每条线路上的顾客数及顾客需求货物量就会确定下来；2）然后再对每辆车单独设计装箱方案，确保全部货物装箱并满足所有装箱约束；3）如果所有车辆都能完成装箱，则最优配送方案产生，否则，重新计算最优配送线路并安排装箱，如此循环。在此求解思路之上，本文提出一种改进的遗传算法和引导式局部搜索算法结合的混合算法进行求解，改进的遗传算法（Genetic Algorithm，GA）求解车辆路径问题，引导式局部搜索算法（Guided Local Search，GLS）求解装箱问题。

在2.1节中提出改进遗传算法，在2.2节中给出引导式局部搜索启发式算法，在2.3节中提出完整的混合启发式算法。

2.1遗传算法

遗传算法是一种有效的全局搜索算法，由美国Michigan大学的J. Holland教授在1975年提出。遗传算法是一种并行搜索算法，模拟自然进化中的自然选择和优胜劣汰极值，主要包括染色体种群、选择算子、交叉算子和变异算子等部分。本节给出遗传算法各部分的策略，并根据3L-MDCVRP的特点提出一些改进策略。

1）编码规则。根据3L-MDCVRP模型中存在多个车场的特点，本文提出两段式编码方式，把染色体分为每个配送中心每辆车服务顾客数和车辆服务顾客顺序。假设有2个配送中心、10个顾客、每个配送中心都有2辆车，则可给出一个染色体编码方式，如图4所示。

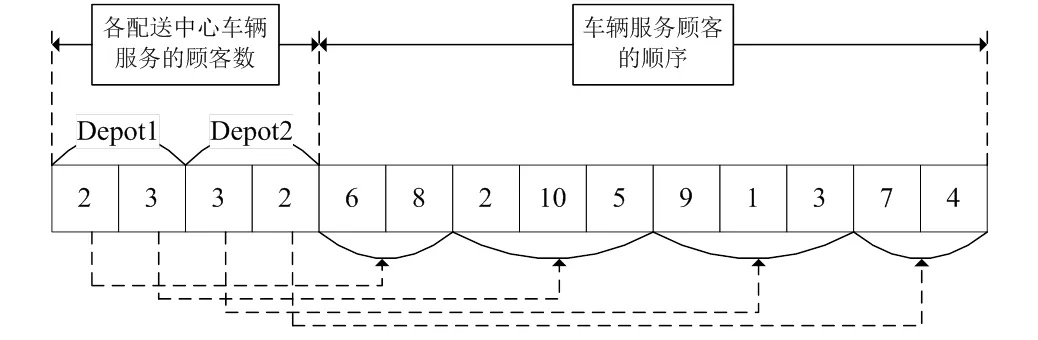
图4 染色体编码方案

图4中给出的染色体可表示如下配送方案：配送中心1的第一辆车按顺序服务顾客6和8，配送中心1的第二辆车按顺序服务顾客2、10和5；配送中心2的第一辆车按顺序服务顾客9、1和3，配送中心2的第二辆车按顺序服务顾客7和4。

2）适应度函数。一般文献中采用目标函数的倒数作为染色体适应度，但是这样计算出的适应度值会比较小，且处理不同问题时取值范围相差很大，因此泛化能力较差。本文提出如下公式作为适应度函数：

3）选择算子。选择算子提供了遗传进化的驱动力，驱动力太大则遗传搜索会过早终止，驱动力太小则进化过程会非常缓慢。本文采用Holland提出的轮盘赌选择策略，其基本原理是根据每个染色体适应度的比例来确定该个体的选择概率或生存概率[16]。

4）交叉算子。交叉操作是交换两个父代染色体部分基因的遗传操作。根据交叉概率选择进入配对池的父代个体，把配对染色体的部分基因加以替换重组，产生子代个体。根据染色体编码由两部分组成的特点，本文提出一种混合交叉算子，具体操作方式为：第一部分采用均匀交叉；第二部分采用顺序交叉。均匀交叉算子：首先随机产生一个与染色体第一部分基因串等长的二进制串，0表示不交换，1表示交换，根据二进制串判断是否交换父代个体对应位置上的基因。由于染色体中没有表示配送中心的基因，因此需要采用新的顺序交叉算子。顺序交叉算子：在父代染色体的第一部分基因串中随机选择一个基因，该基因对应的数字作为第二部分基因串的交叉段，然后把交叉段内的基因互换，把换出基因放在换入基因原来的位置上，当父代基因对应的数字不相同时，第二个父代向后移动至数字相同位置，如找不到相同数字则取消本次交叉操作。如图5所示，以A和B两个父代个体为例进行混合交叉操作，X为二进制串，设产生的子代个体为C和D。

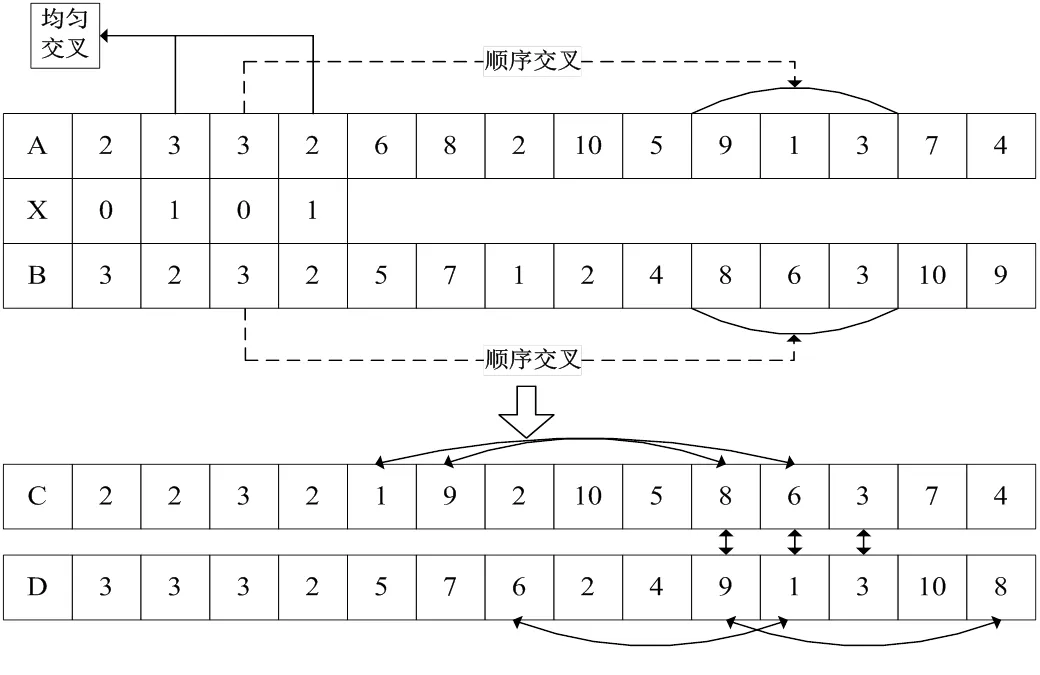
图5 染色体交叉操作

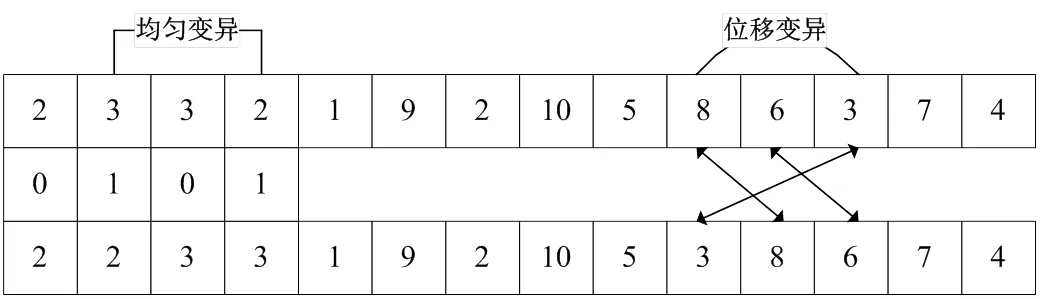
图6 染色体变异操作

6）非可行解调整。经过交叉操作和变异操作，染色体对应的解可能变成非可行解，因此需要对其进行调整。顾客数是固定的，因此染色体第一部分基因串上的数字之和必须等于顾客数，当基因值之和小于顾客数时，随机选择一个基因值加1，当基因值之和大于顾客数时，随机选择一个基因值减1，重复操作至基因值之和与顾客数相等为止。在生成初始种群及进行遗传操作的时候，可能会有一些染色体不符合模型中的一个或多个约束条件。显然对于本文的染色体编码方式，所有染色体都自然满足约束（2）、（3）、（8）和（9），因此，调整非可行解的时候只须检查约束（4）、（5）、（6）和（7）。采用的约束控制策略是根据染色体对约束的违反程度降低其适应度值。

6）记忆库。为了减少3L-CVRP的求解时间，本文在遗传算法中加入记忆库机制，具体作用在后面给出，这里只给出记忆库的形成原理。设定记忆库的最大规模为，把每代种群中的最优个体保存到记忆库中，当最优个体数超过记忆库规模时，去掉记忆库中适应度最小的个体。当遗传算法达到最大迭代次数之后，把当前种群全部加入记忆库中，按适应度值从大到小排列所有个体，删除适应度较小的个体，维持记忆库规模为。

2.2引导式局部搜索

本节讨论如何把货物装入车厢内，且满足第1章中的装载约束。一般装箱问题以装载货物数最大为目标，而3L-MDCVRP的装箱问题中每辆车装载的货物数是固定的，因此其解空间仅是一般装箱问题解空间的一个子集。针对这样的特点，设计算法的时候只须要在局部进行搜索即可，通过一系列的引导策略寻找问题的局部最优解。3L-MDCVRP的装箱过程包括确定货物的装载顺序和寻找可行的装货位置两个子问题，下面分别给出这两个子问题的求解策略：

3）可行装货位置顺序。初始可行装货位置均在（0,0,0）点上，如图7-a所示。装入一个货物之后，可行装货位置更新，产生A1、A2和A3三个可行装货位置，如图7-b所示。对于装货序列中的下一个待装货物，需要给出一个可行装货位置的顺序，然后逐个扫描这些位置，直至找到一个满足所有装载约束的可行位置，每个货物需要在两个方向上进行扫描（水平方向可旋转90度）。本文采用引导式排序方法给出可行装货位置顺序，引导式排序方法包括“Back-Left-Low”、“Left-Back-Low”、“Max-Touching-Area-Y”、“Max-Touching-Area-No-Walls-Y”、“Max-Touching-Area-X”及“Max-Touching-No-Walls-X”等六种[17]，依次选择六种方法中的一个，直至找到可行装载方案。六种规则的具体操作方法可参考文献[17]。

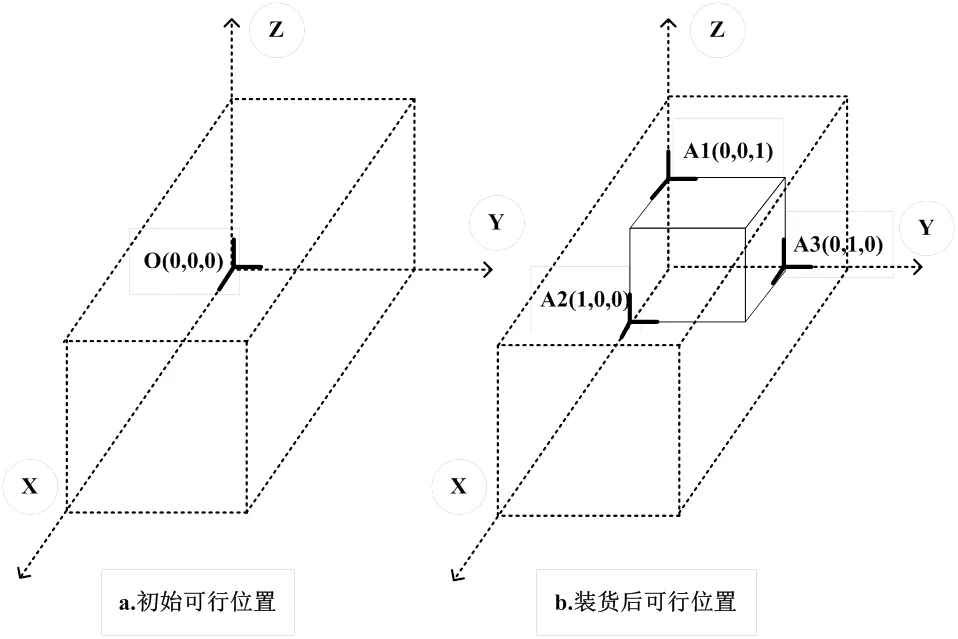
图7 可行装货位置示意图

2.3混合启发式算法

本文把改进遗传算法和装箱启发式算法结合起来，构造求解3L-MDCVRP的引导式局部搜索遗传算法（Guided Local Search Genetic Algorithm，GLSGA）。GLSGA的基本思路为：通过改进遗传算法得出VRP的近似最优解，近似最优解保存在记忆库中；把记忆库中的个体按适应度值从大到小排列，选择第一个解作为当前车辆路线方案，然后调用装箱问题的启发式算法；如果找到可行装箱方案，则返回最优解，否则，选择记忆库中的下一个解作为车辆路线方案；如果记忆库中所有车辆路线方案均找不到可行解，则返回遗传算法重新求解VRP；重复算法直至找到可行解，或达到最大迭代次数。

GLSGA的具体步骤如下：

Step2.遗传算法参数初始化：设定遗传算法的种群规模和记忆库规模，设定交叉概率和变异概率，确定最大迭代次数，令；

Step3.初始种群生成：对染色体进行编码，用随机方法产生初始种群；

Step4.记忆库更新：计算染色体适应度，把当前种群中的最优个体保存进记忆库，若记忆库规模超过，则去掉适应度值较小的个体；

Step5.遗传操作：对当前种群进行选择、交叉和变异等遗传操作；

Step7.近似最优解集生成：遗传算法终止，把当前种群全部加入记忆库中，并按适应度值排列染色体，保留适应度值最大的个染色体形成近似最优解集；

Step10.初始装货序列：按照车辆服务顾客顺序的相反顺序排列货物，相同顾客的货物按照非易碎品在前、易碎品在后的顺序排列；

Step13.可行装货位置循环：若所有货物均找到可行装货位置，算法终止，输出当前最优解；若有一个或多个货物没找到可行装货位置，且，令，返回Step12；若，转Step14；

GLSGA算法流程如图5所示。

图5 GLSGA算法流程图

3数值试验

数值试验平台为：Matlab 7.1，计算机CPU为英特尔酷睿2、2.67GHz，2GB内存，32位windows 7操作系统。

由于标准算例库中的问题均为单配送中心问题，因此本人设计两个数值模拟试验：第一个试验针对标准算例进行计算，检验GLSGA算法的有效性；第二个试验针对随机数据进行仿真，检验模型的可解性。

3.1标准算例库试验

目前研究3L-CVRP问题的文献较少，作者能够搜集到的全部相关文献均已附在参考文献中。已发表的文献均直接采用文献[7]的模型，模型同时处理车辆路径问题和装箱问题，并提出一些不同的算法进行求解，同时以文献[7]给出的标准算例库进行数值试验。目前，该算例库是仅有的3L-CVRP标准算例库，针对文献[7]的标准算例进行数值试验，以检验本文所提出新算法的性能。

算例库中总计包括27个3L-CVRP标准算例。算例包含的信息有：配送中心坐标，顾客数及顾客坐标；每个顾客需求的货物及其需求货物的重量；每个货物的长、宽、高，易碎品与非易碎品标识；配送中心拥有车辆数，车辆最大载重，车厢的长、宽、高。货物堆叠的时候，支撑面积与上层货物底面积的比例最小值为=0.75。

为了在检验算法性能的时候避开模型的影响，该试验直接采用文献[7]的模型，使用本文设计的GLSGA算法进行求解。表1给出满足所有装箱约束的计算结果，以及与其它文献计算结果的比较。

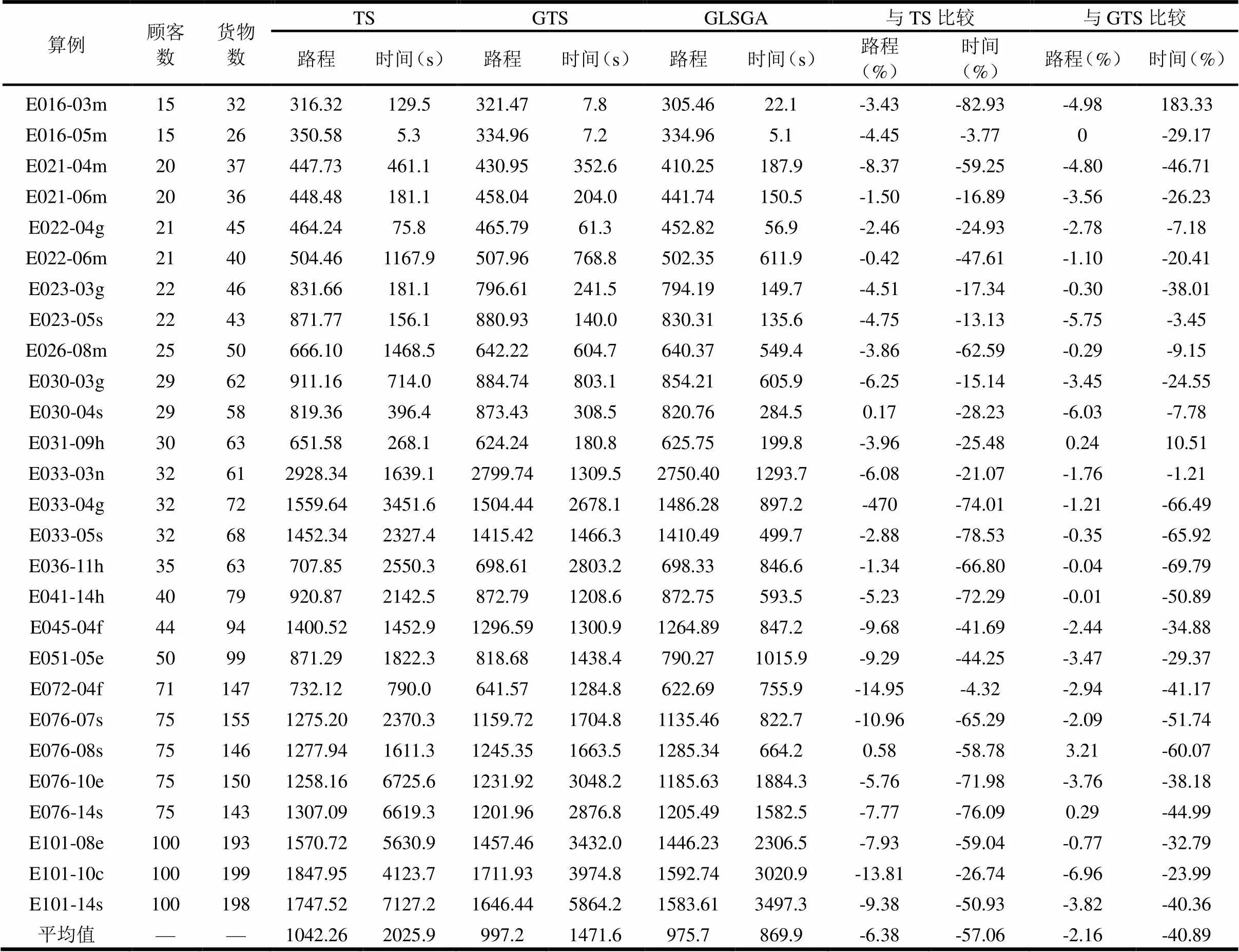
表1 3L-CVRP算例计算结果及与其它方法比较

从计算结果上看，GLSGA算法的计算结果较TS算法和GTS算法有明显的改善，27个标准算例的车辆行驶路程几乎全部减少。与TS算法相比平均路程减少6.38%、最大减幅为14.95%，与GTS算法相比平均路程减少2.16%、最大减幅6.96%。从计算时间上看，GLSGA算法较TS算法和GTS算法有大幅度的降低，与TS算法相比平均时间减少57.06%、最大减幅为82.93%，与GTS算法相比平均时间减少40.89%、最大减幅为69.79%。通过与已有文献的计算结果相比，表明GLSGA算法具有良好的计算性能和较高的计算效率。由于已有文献的模型均采用Iori提出的基本3L-CVRP模型，而该试验直接在模型上运行GLSGA算法，因此可以判断本文得到的计算结果是由GLSGA算法产生的。

3.2随机数据仿真试验

在验证了GLSGA算法的有效性之后，可以用该算法求解3L-MDCVRP模型。首先，给出一个有2个配送中心、20个顾客、每个配送中心有4辆车（车辆限重500、限容1000）的3L-MDCVRP实例，表2给出随机产生的配送中心和顾客节点坐标，表3、表4给出每个顾客需求的货物规格。

计算得出5条线路，总有效路程为4.2435，所有车辆均满足装箱约束，最优配送路径如图9所示。

R1={Depot1-13-11-12-10-Depot1}，总路程为1.0376，载货总重为302，载货总体积为795；

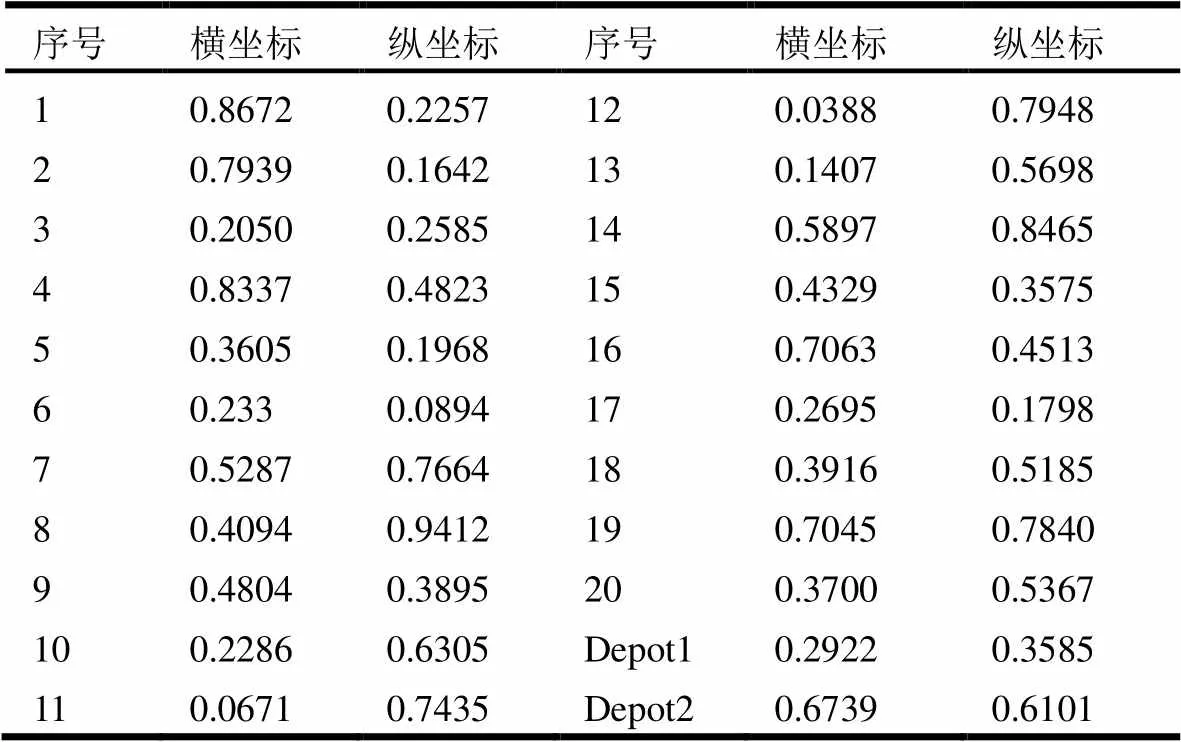
表2 随机产生的配送中心和顾客节点坐标

R2={Depot1-3-6-17-5-Depot1}，总路程为0.6697，载货总重为342，载货总体积为561；

R3={Depot1-15-9-18-20-Depot1}，总路程为0.5773，载货总重为400，载货总体积为508；

R4={Depot2-7-8-14-19-Depot2}，总路程为0.9359，载货总重为391，载货总体积为855；

R5={Depot2-16-2-1-4-Depot2}，总路程为1.023，载货总重为426，载货总体积为706。

表3每个顾客需求的货物规格

顾客序号货物序号顾客序号货物序号顾客序号货物序号顾客序号货物序号 121,76171119169,22 223718,12125,25174 3308241331827,1 410,26,1698,21429,281914,15 51110201513206

表4货物规格（长、宽、高及重量）

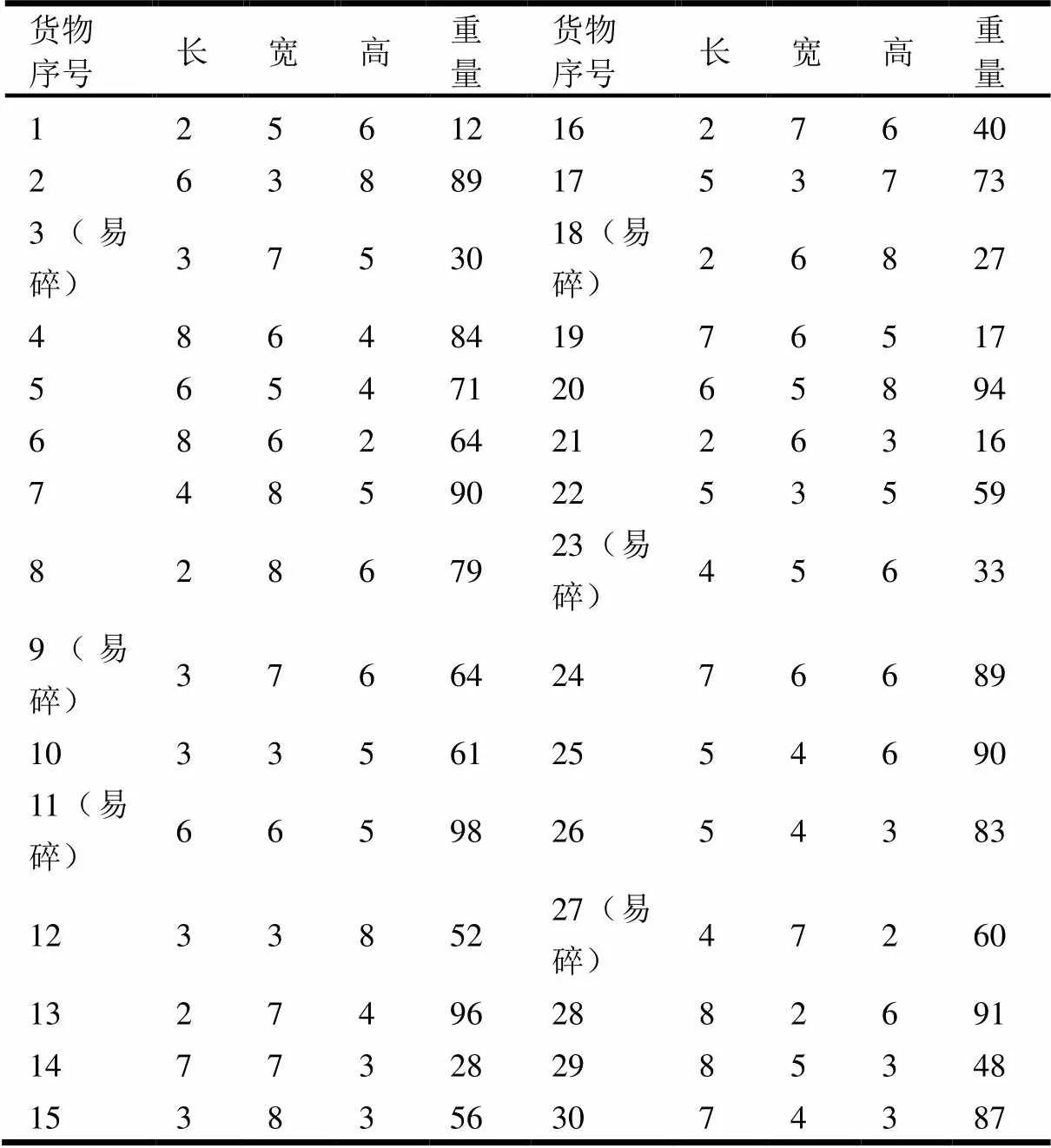
货物序号长宽高重量货物序号长宽高重量 1256121627640 2638891753773 3（易碎）3753018（易碎）26827 4864841976517 5654712065894 6862642126316 7485902253559 82867923（易碎）45633 9（易碎）376642476689 10335612554690 11（易碎）665982654383 123385227（易碎）47260 13274962882691 14773282985348 15383563074387

图9 最优配送路径示意图

4结论

本文研究多车场车辆路径和三维装箱相结合的组合优化问题，在3L-CVRP模型中首次考虑多车场的情况，建立3L-MDCVRP模型，并提出遗传算法和引导式局部搜索算法结合的GLSGA算法进行求解，针对3L-MDCVRP问题的特点提出遗传算法的改进策略。本文设计了标准算例库和随机数据两个数值试验，两个试验均取得了非常理想的结果。首先采用27个标准算例检验GLSGA算法的性能和效率，试验结果表明GLSGA算法能够很好的处理3L-CVRP这类问题。然后根据3L-MDCVRP模型的要求随机生成仿真数据进行测试，试验结果表明3L-MDCVRP模型可以用GLSGA算法进行求解。

3L-MDCVRP建立了考虑多车场和三维装箱的物流配送模型，极大地满足了实际物流配送的要求。下一步还可以考虑加入时间窗、多车型等更多因素的模型，并根据实际情况设计不同的目标函数建立模型，从理论上进一步完善3L-CVRP模型体系。

[1] Iori M. Meta-heuristic algorithm for combinatorial optimization problems[J]. 4OR: A Quarterly Journal of Operations Research, 2005, 3(2): 163-166.

[2] Iori M,Salazar-Gonzalez JJ, Vigo D. An exact approach for the vehicle routing problem with two-dimensional loading constraints[J]. Transportation Science, 2007, 41(2): 253-264.

[3] Gendreau M, Iori M, Laporte G,. A tabu search heuristic for the vehicle routing problem with two-dimensional loading constraints[J]. Networks, 2008, 51(1): 4-18.

[4] Khebbache S, Prins C, Yalaoui A,. Memetic algorithm for two-dimensional loading capacitated vehicle routing problem with time windows[C]. International Conference on Computers and Industrial Engineering, 2009, 1(3): 1110-1113.

[5] Leung S, Zheng J, Zhang D,. Simulated annealing for the vehicle routing problem with two-dimensional loading constraints[J]. Flexible Services and Manufacturing Journal, 2010: 1-22.

[6] Leung SCH, Zhou X, Zhang D,. Extended guided tabu search and a new packing algorithm for the two-algorithm loading vehicle routing problem [J]. Computers & Operations Research, 2011, 38(1): 205-215.

[7] Gendreau M, Iori M, Laporte G,. A tabu search algorithm for a routing and container loading problem[J]. Transportation Science, 2006, 40(3): 342-350.

[8] Moura A, Oliveira J. An integrated approach to the vehicle routing and container loading problems[J]. OR Spectrum, 2009, 31(4): 775-800.

[9] Fuellerer G, Doerner KF, Hartl RF,. Metaheuristics for vehicle routing problems with three-dimensional loading constraints[J]. European Journal of Operational Research, 2010, 201(3): 751-759.

[10] Iori M, Martello S. Routing problems with loading constraints[J]. TOP, 2010, 18(1): 4-27.

[11] 马珊静，陈峰，宋德朝，越库配送物流系统车辆调度算法的研究[J]. 现代制造工程，2009（1）：12-15，127.

[12] 宁爱兵，熊小华，马良. 城市物流配送中的三维装箱算法[J]. 计算机工程与应用，2009，45（9）：207-208，211.

[13] 王征，胡祥培，王旭坪. 带二维装箱约束的物流配送车辆路径问题[J]. 系统工程理论与实践，2011，31（12）：2328-2341.

[14] Ruan QF, Zhang ZQ, Miao LX,. A hybrid approach for the vehicle routing problem with three-dimensional loading constraints[J]. Computers & Operations Research, 2011, 38(11): 1-11.

[15] Junqueira L, Morabito R, Yamashita DS. Three-dimensional container loading modes with cargo stability and load bearing constraints[J]. Computers & Operations Research, 2012, 39(1): 74-85.

[16] Holland J. Adaptation in Natural and Artificial System[M]. Cambridge: MIT Press, 1992.

[17] Tarantilis CD, Zachariadis EE, Kiranoudis CT. A Hybrid Metaheuristic Algorithm for the Integrated Vehicle Routing and Three-Dimensional Container-Loading Problem[C].Transactions on Intelligent Transportation Systems, 10(2): 255-271.

Multi-Depots Vehicle Routing Problem with Three-Dimensional Loading Constraints

YAN Rui1, ZHANG Qun2, HU Rui2

(1. School of Economics and Management, Beijing Information Science & Technology University, Beijing 100192, China;2. Dongling School of Economics and Management, University of Science & Technology Beijing, Beijing 100083, China)

The 3L-MDCVRP (Three-Dimensional Loading Multi-Depots Capacitated Vehicle Routing Problem, 3L-MDCVRP) is a new proposed optimization problem, which is a combination of loading problem and VRP problem based on multi-depots. There are several constraints for 3L-MDCVRP: 1) the demand of a certain set of customers; 2) a feasible placement of items within the loading space;and 3) a fleet of identical vehicles of limited capacity based onseveral depots.Loading items into vehicles and successive routing of vehicles along the road network are the most important problems in distribution management.

This paper addressed an important problem combining three-dimensional loading and multi-depots vehicle routing problems. A brand new solution has been proposed. The new algorithm was a combination of two intelligent algorithms and it passed the test with good performance.

Both the capacity vehicle routing problem and three-dimensional problem are NP-hard problems.Thus,the combinatorial problem 3L-MDCVRP is clearly also the case. Exact algorithmic methodologies are not expected to solve the real-world problems of large customers and item sets in a reasonable time. Therefore, we solve the problem by using a heuristics algorithm named Guided Local Search Genetic Algorithm (GLSGA), which makes use of fast packing heuristics for the loading. The hybrid algorithm combines two different heuristic information measures: a genetic algorithm for routing because of its specialty in finding local optima, and a guided local search algorithm for loading.

The algorithm was tested on the set of benchmark instances proposed by Gendreau and Iori. These instances were the only 3L-CVRP instances available in all publications. It had been shown that the new algorithm had a better performance than the benchmark approach when all loading restrictions were satisfied.Both the distance and calculationtime were significantly reduced.There was a 6.38% decrease compared with TS in distance and a 2.16% compared with GTS. In addition, there was a 57.06% reduction compared with TS in calculationtime and 40.89% compared with GTS.

After the efficiency of GLSGA had been proved, it was applied in an experiment of 3L-MDCVRP instance, which was generated randomly. The algorithm derived the solution pretty and all five results were available in the real delivery process after checking.This new GLSGA was capable of improving the efficiency of solving 3L-MDCVRP, which was quite meaningful in the distribution process since it was able to control logistics cost and increase the utilization of vehicles.

vehicle routing problem; multi-depots; three-dimensional packing; genetic algorithm

中文编辑：杜 健；英文编辑：Charlie C. Chen

0224

A

1004-6062(2016)01-0108-09

10.13587/j.cnki.jieem.2016.01.013

2012-11-12

2013-09-09

国家重点基础研究发展规划资助项目（973，子课题）(2010CB955903-1)；国家自然科学基金资助项目（71172168）

颜瑞（1986—），男，江苏连云港人，博士研究生，研究方向：物流优化、车辆路径。