联合稀疏表示和总变分正则化的超分辨率重建方法*

黄炜钦 黄德天 柳培忠 顾培婷 刘晓芳



联合稀疏表示和总变分正则化的超分辨率重建方法*

黄炜钦 黄德天 柳培忠 顾培婷 刘晓芳

华侨大学工学院

为提高基于稀疏表示的图像超分辨率重建的质量，该文提出了联合稀疏表示与总变分正则化的超分辨率重建算法。首先，在字典训练阶段，从具有相似统计特征的训练图片中获取图像块，作为训练字典的样本，并用K-SVD算法进行字典训练，得到高、低分辨率的字典。在稀疏编码阶段，根据局部稀疏编码模型求解出低分辨图像的稀疏表示系数，再利用稀疏表示系数和高分辨率字典对输入低分辨率图像进行重建，得到高分辨率图像。最后，将重建得到的高分辨率图像进行总变分正则化优化，进一步提高重建效果。仿真实验结果表明，该算法在客观评价指标和主观视觉效果上，图像质量都有明显提高。

超分辨率重建 稀疏表示 总变分正则化 字典训练

1 概述

图像的空间分辨率用于衡量图像质量，图像的空间分辨率越高说明图像越清晰，细节信息越丰富，图像质量越高，其表达信息的能力就越强，越有利于后续的图像处理、分析和理解。在实际应用中，受成像系统物理分辨率限制以及场景变化等诸多因素的影响，成像系统只能得到分辨率较低的图像，往往不能满足实际应用的要求[1-4]，如何基于已有硬件条件及当前的观测图像提高图像分辨率，成为一个亟待解决的问题。

图像超分辨率(Super Resolution, SR) 重建技术[5]一直以来都是数字图像处理的研究热点之一，该技术是从软件方面通过一些相关算法将低分辨率(Low Resolution, LR)图像重建为清晰的高分辨率(High Resolution, HR)图像。该技术利用已有的低分辨率图像重建出高分辨率图像，能够突破现有成像器件的固有限制,只从软件的角度实现高分辨率图像的重建，是解决该问题较为经济而有效的手段之一。

当前，基于插值的方法、基于重建的方法和基于学习的方法是单幅图像超分辨率重建的三种主要方法。基于插值的算法主要包含二次插值和双三次插值[6]等方法，该算法虽然实现起来较为简单，但是重建出来的图像经常存在锯齿效应，并且锯齿效应会随着图像放大而更为明显。基于重建的方法[7]主要利用图像的相关先验知识来建立超分辨率的模型，但是先验模型选取受主观因素影响较大，所以该方法缺乏一定的自适应性，重建的效果不好。近年来，比较流行的方法是基于学习的图像超分辨率方法，该方法根据相似的训练集训练字典，来预测低分辨率图像中丢失的细节信息，从而完成图像重建。作为基于学习的最为突出的算法之一，基于稀疏表示的图像超分辨率重建由Thomas Huang 团队里的Yang开创，并吸引了国内外学者的广泛研究。Yang等[8]将大量高分辨率图像组成的图像库作为训练样本，通过全局字典学习构建能够稀疏表示图像块的字典；假设高分辨图像块的稀疏系数可由低分辨图像块的稀疏系数来表示，首先利用低分辨图像块和低分辨字典获得低分辨率系数，然后利用求得的低分辨系数和训练好的高分辨字典重建出高分辨率图像块。该算法获得的重建图像虽然具有较好的视觉效果，但一般存在较大的均方误差，且当图像库不能提供与待处理图像相似的图像块时，算法的重建效果将无法保证。Zeyde等[9]在基于超完备字典学习的稀疏表示超分辨算法的基础上进行了改进，将主成分分析方法用于图像的降维，并且将正交匹配追踪算法应用于稀疏编码，在一定程度上，虽然该方法提高了图像重建的速度，但是重建图像的精度并没有明显提高。Elad等[10]在基于稀疏表示的单幅图像超分辨重建中，利用统计预测模型来稀疏表示低分辨率图像块和高分辨率图像块，并采用误差平方和均值最小估计得到高分辨率图像块的预测，得到了比基于双字典的超分辨率更好的重建效果。文献[11]在假设可以得到一对字典使得高低分辨率图像块具有相同的稀疏表示的前提下，通过训练分类样本以得到两个字典，为了获得更准确的稀疏系数，选取细节图像块作为方法的对象。该算法可以减少重建伪像，一定程度上提高了重建精度。Sajjad等[12]主要利用图像的边缘、轮廓和高阶结构等特征来训练字典，通过求解L1正则化最小平方问题来获得高低分辨率图像块之间的稀疏表示矢量，并通过所学习的字典来重构高分辨图像，算法取得了较好的重建效果。文献[13]先采用稀疏表示方法从输入的低分辨率图像生成保留边缘的高分辨率图像，再结合上下文感知检测方法，利用跨尺度自相似性生成细节推测的高分辨图像，最后通过这两个高分辨图像进行加权得到清晰的重建图像。

为了对超分辨率重建后的图像进行进一步的优化和恢复，Rudin等[14]首次提出总变分正则化模型，并将该正则化模型应用于图像去噪处理。本文将总变分思想融入到文献[15]中，对该文献重建后的高分辨率图像进行进一步优化，以此对图像进一步降噪、去卷积和图像修复，从而进一步提高重建图像的质量。

2 基于稀疏表示的超分重建模型

上式中，表示降采样操作，表示糊化矩阵，表示为运动变换算子，表示为随机的高斯加性噪声。通过稀疏表示模型来求解图像重建这个具有病态性的反问题，在满足一定的条件下，式(1)存在唯一的稀疏解。

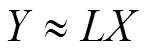
(3)

从式(3)可以看出，在图像的稀疏表示中引入了稀疏求解这一约束条件，而0范数问题的求解是一个NP 难问题，并且对于0范数问题的求解计算量大，而1范数是接近0范数的凸优化问题，所以，在稀疏度足够大的情况下，0范数的求解问题可以等价转换为1范数求解，即：

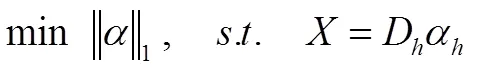
图像的超分辨率重建就是通过由已知的来对进行重建。但是复杂随机的决定了重构任务的不确定性。由信号的稀疏表示可知，理想的图像可以表示为，对应的图像可以表示为，联合式(2)有：

(5)

如果选择合适的字典对，则图像在D字典下的稀疏表示系数可近似由对应的图像在D字典下的稀疏表示系数来表示，即有。定义，则有：

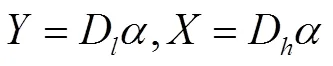
式(6)表明，当通过学习获得高、低分辨率字典对后，可以由求得稀疏表示系数，然后由不同分辨率图像的稀疏表示的不变性，通过重建出高分辨率图像。

3 基于稀疏表示和总变分全局优化的超分重建

3.1 字典训练

实验中，本文从具有相似统计特征的训练图片中随机获取原始图像块来训练生成字典，需要准备的字典训练过程如下：

3.1.1 样本采集

本文需要采用自然景观图像作为训练集，这些图像样本训练集有一定的纹理。对于字典的训练，本文取30张高清图像作为高分辨率图像训练样本，然后对着30张图像进行下采样，得到30张对应的低分辨率图像，并把它们分为100000个图像块，这个训练集远小于文献[16]所需要的训练样本。

3.1.2 字典对的训练

每个高分辨率训练图像都有其对应的通过下采样得到的低分辨率图像。将和分块，组成训练集和，记为图像对应的稀疏编码矩阵，为图像对应的稀疏编码矩阵，利用K-SVD算法来求解以下优化问题：

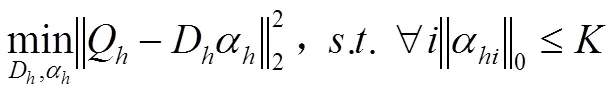
(8)

由式(7)和(8)可以得到高、低分辨率字典对，分别表示为，。

在训练阶段，本文减去每个图像块的平均像素值，让字典表示的是图像的纹理而不是绝对的强度。实验证明，在结合稀疏表示的先验知识的条件下，简单随机采样得到的字典已经足以生成高质量的重建图像。

3.2 局部稀疏编码

在字典训练阶段，得到了高低分辨率字典对D和D。对于每一个输入的低分辨率图像块，本文得到一个与低分辨率字典D相对应的稀疏表示。高分辨率的图像块字典D会根据这个稀疏表示系数来生成所要输出的高分辨率图像块。通过式(9)，可以得到低分辨率图像块的稀疏表示系数：

其中，是一个线性提取操作，目的是为了确保计算出的系数更加适合低分辨信号。一般的，是一种高通滤波器，因为人对图像的高频部分是比较敏感的，所以使用高通滤波器来获取低分辨率图像中的高频部分，用来估计丢失的高频信息。文献[15]将一阶和二阶导数作为低分辨率图像块的特征，尽管简单，但是这些特征证明的效果极好。四个用于倒数提取的一维滤波器如下：

(10)

其中，表示转置。使用这四个滤波器，每个图像块可以得到四个描述特征向量，然后把这四个特征向量联合起来，作为低分辨率图像的最后表示。通常式(9)的优化问题是NP难问题，文献[15]采用最小化1范数来求解稀疏表示系数，如式(11)所示：

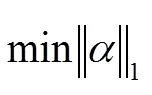
3.3 总变分正则化优化图像

本文提出的图像恢复方法是基于Rudin-Osher-Fatemi总变分(TV)图像恢复技术[17]，将上一阶段得到的图像进行总变分正则化优化。本文需要构造一个基于总变分正则项理论的图像去噪、去卷积和修复图像的恢复模型，该模型需要满足的条件是找到一个图像，使得式(12)取得最小：

(13)

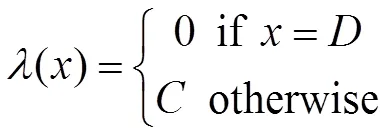
接下来解决式(12)的最小化问题。由于Split-Bregman方法是一种用来解决规则化问题的快速方法，也适用于各种各样的TV正则化问题，效率高，可靠性强，本文采用文献[14]所使用的Split- Bregman算法来求解优化后的图像。

3.4 算法步骤

综合以上分析，本文具体步骤总结如下：

步骤1：对高分辨率训练样本图像进行下采样，得到低分辨率样本图像。

步骤2：将和分块，分别得到高、低图像子块和。

步骤4：结合与D通过求解式子来求得低分辨率图像的稀疏表示矩阵。

步骤6：将图像进行总变分正则化优化，得到优化图像。

4 实验结果与分析

实验的软硬件环境为：计算机CPU 为Intel Core i5-4590 3.30 GHz，内存4GB，操作系统为Windows64,MATLAB 为2012b。

图像评价主要包括客观评价和主观评价，其中客观评价指标主要是峰值信噪比(PSNR)和结构相似性度量(SSIM)。PSNR值越高，表示重构的图像质量好，SSIM值越大，表明重构图像与原始图像越相似，重建效果越好。

为了验证本文算法的性能，在实验中采用大量测试图像进行实验。实验时，低分辨率图像块放大倍数为3倍。实验结果与双三次插值算法和文献[15]提出的算法进行比较。表1给出了10幅测试图像利用3 种算法得到的PSNR值和SSIM 值。由表1 可以看出，10幅图像中，本文算法获得的PSNR和SSIM都是最高，这说明本文算法能够更好地恢复图像的结构，提高图像的重建质量。

图1从主观方面展示了本文提及的三种重建方法的重建效果。图1自左往右分别表示为低分辨率图像、双三次插值、文献[15]提出的算法和本文算法重建的高分辨率图像，以及原始高分辨率图像，分别用(a)、(b)、(c)、(d)、(e)表示。从中可见，本文重建的图像有更好的全局视觉效果。

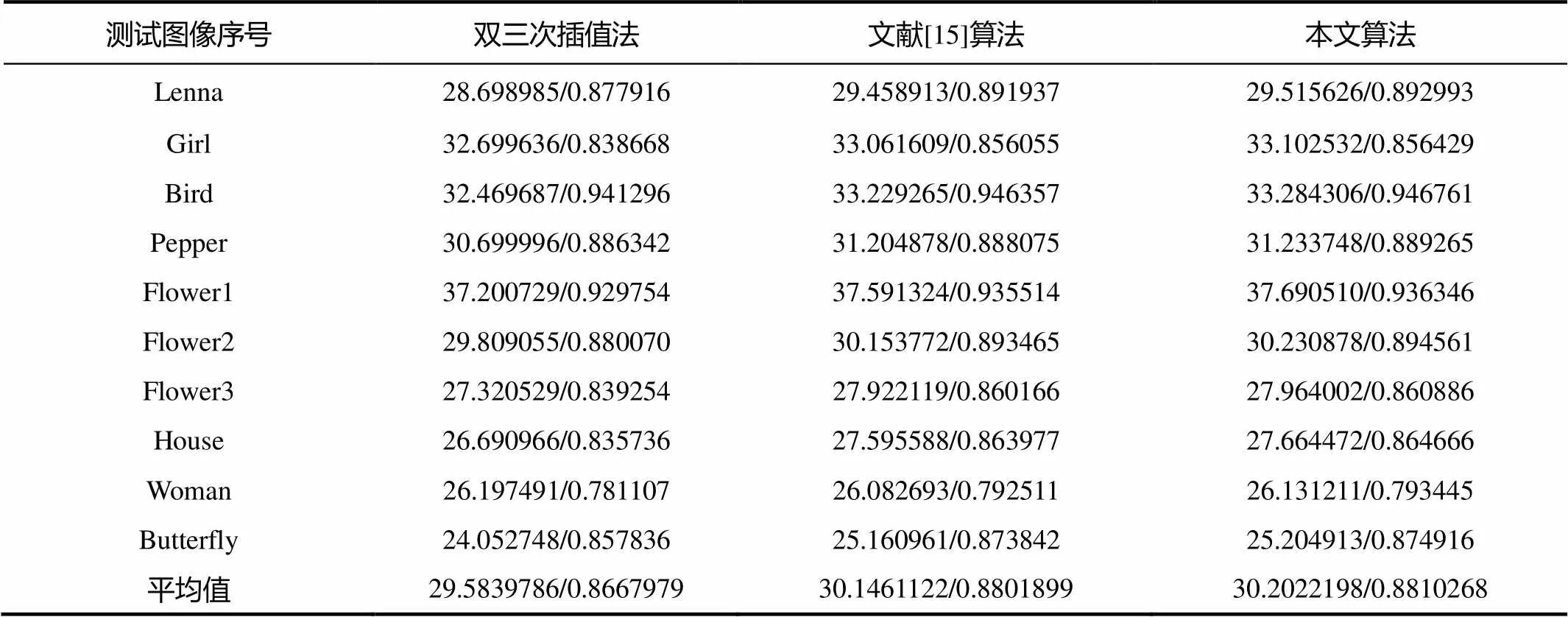
表1 PSNR和SSIM下不同算法重建效果的比较(PSNR/SSIM)

5 结束语

本文提出的图像超分辨率重建算法是一种结合稀疏表示和总变分正则化的超分辨率重建方法，该算法利用了总变分正则化在图像降噪、去卷积和修复效果好的特点，通过对基于稀疏表示重建出的图像进一步优化处理，以此提高重建的质量。实验结果表明，与多种超分辨率算法相比，本文算法具有较好的超分辨重建效果，但是效果还有一定的提升空间，如何更好地利用总变分进行图像恢复与优化，是今后需要进一步研究的课题。

参考文献:

[1] Zhang L, Zhang L, Mou X, et al. FSIM: a feature similarity index for image quality assessment[J]. IEEE Transactions on Image Processing, 2011, 20(8): 2378-2386.

[2]Pok G, Liu J C, Nair A S. Selective removal of impulse noise based on homogeneity level information.[J]. IEEE Transactions on Image Processing, 2003, 12(1):85-92.

[3] Foi A, Katkovnik V, Egiazarian K. Pointwise shape-adaptive DCT for high-quality denoising and deblocking of grayscale and color images.[J]. IEEE Transactions on Image Processing, 2007, 16(5): 1395-1411.

[4] Banham M R, Katsaggelos A K. Digital image restoration[J]. IEEE Signal Processing Magazine, 1997, 14(2):24-41.

[5] Kang M G, Chaudhuri S. Super-resolution image reconstruction[J]. IEEE Signal Processing Magazine, 2003, 20(3):19-20.

[6] Hou H S, Andrews H. Cubic splines for image interpolation and digital filtering[J]. IEEE Transactions on Acoustics Speech & Signal Processing, 1979, 26(6):508-517.

[7] Multiple frame image restoration and registration[C]// Advances in Computer Vision & Image Processing Greenwich Ct, Jai Press Inc, 1984.

[8] Yang J, Wright J, Huang T S, et al. Image super-resolution via sparse representation[J]. IEEE Transactions on Image Processing, 2010, 19(11): 2861-2873.

[9] Zeyde R, Elad M, Protter M. On Single Image Scale-Up Using Sparse- Representations[C]// International Conference on Curves and Surfaces, Springer-Verlag, 2010:711-730.

[10] Peleg T, Elad M. A Statistical Prediction Model Based on Sparse Representations for Single Image Super-Resolution[J]. IEEE Transactions on Image Processing, 2014, 23(6):2569-82.

[11] Zhao Y, Chen Q, Sui X, et al. A novel infrared image super-resolution method based on sparse representation[J]. Infrared Physics & Technology, 2015, 71:506-513.

[12] Sajjad M, Mehmood I, Baik S W. Image super-resolution using sparse coding over redundant dictionary based on effective image representations[J]. Journal of Visual Communication & Image Representation, 2014, 26(C):50-65.

[13] Lu J, Sun Y. Context-aware single image super-resolution using sparse representation and cross-scale similarity[J]. Signal Processing Image Communication, 2015, 32(C):40-53.

[14] Rudin L I, Osher S, Fatemi E. Nonlinear total variation based noise removal algorithms [J]. Physica D-nonlinear Phenomena, 1992, 60(1-4):259-268.

[15] Yang J, Wright J, Huang T, et al. Image super-resolution as sparse representation of raw image patches[C]// IEEE Conference on Computer Vision and Pattern Recognition, 2008:1-8.

[16] Sun J, Zheng N N, Tao H, et al. Image Hallucination with Primal Sketch Priors[C]//2012 IEEE Conference on Computer Vision and Pattern Recognition, IEEE Computer Society, 2003:729.

[17] Goldstein T, Osher S. The split Bregman method for L1 regularized problems[J]. Siam Journal on Imaging Sciences, 2009, 2(2): 323-343.

华侨大学研究生科研创新能力培育计划资助项目。