基于模糊数学-层次分析法的水泥胶结充填料浆配比优化研究
2016-10-14石文芳许杨东陈忠熙姜亮亮
罗 涛,何 文,石文芳,许杨东,陈忠熙,姜亮亮
(1.江西理工大学资源与环境工程学院, 赣州 341000;2.江西理工大学江西省矿业工程重点实验室,赣州 341000)
基于模糊数学-层次分析法的水泥胶结充填料浆配比优化研究
罗涛1,2,何文1,2,石文芳1,2,许杨东1,2,陈忠熙1,2,姜亮亮1,2
(1.江西理工大学资源与环境工程学院, 赣州341000;2.江西理工大学江西省矿业工程重点实验室,赣州341000)
针对某矿山残矿回采时充填效果存在的问题,采用水泥胶结全尾砂充填。根据充填料浆的力学性质和流动性能,初步确定影响充填效果较大的因素:28 d单轴抗压强度、单位沿程阻力和自然沉降速率。为了进行充填料浆配比优化研究,应用模糊数学和层次分析法分别建立各配比的隶属度矩阵和以上影响因素的权重矩阵,通过模糊决策确定该水泥胶结全尾砂充填料浆的最优配比:灰砂比(水泥用量∶全尾砂用量)1∶4、浓度72%。优化结果表明:在保证料浆充填体的强度前提下,最优配比可以有效改善料浆输送性能,减少充填成本。
抗压强度; 单位沿程阻力; 自然沉降速率; 模糊数学; 层次分析法
1 引 言
充填已成为矿山不可缺少的重要技术,其效果直接影响矿山的经济效益和井下工作人员的生命财产安全。至今,许多矿山出现充填效果不好的现象,导致充填体塌落和充填成本增大等实际问题,严重影响了井下开采的进度和工作人员的安全,因此,进行充填料浆配比的优化可有效改善其充填效果,加快地下开采进度,增加矿山的经济效益。所以,进行充填料浆配比优化研究对井下充填提供重要的理论依据[1,2]。
根据充填料浆的力学性质和流动性能,影响水泥胶结全尾砂充填效果较大的有充填体强度、料浆输送的沿程阻力和料浆的自然沉降速率等。因此,通过单轴抗压强度、流变特性及自然沉降室内试验,计算并得出单轴抗压强度、料浆输送的沿程阻力和料浆的自然沉降速率等试验数据。对以上试验数据进行数据分析,优化其充填料浆的配比[3,4]。
本文以某矿山全尾砂(其粒度分布,见表1)为例,胶结材料:P·O 42.5级水泥。其充填料浆的配比方案有:灰砂比(水泥用量∶全尾砂用量):1∶4、1∶6、1∶8;浓度:68%、70%、72%、74%,共12组。应用模糊数学结合层次分析法对以上12组配比方案的试验数据进行分析,得出该水泥胶结全尾砂充填料浆的最优配比。

表1 粒度分布
2 单轴抗压强度试验
充填体强度测试是参照《建筑砂浆基本性能试验方法标准》(JGJ/T 70-2009)测定充填体试件在特定浓度、配比的单轴抗压强度[5]。本次试验所用设备为RMT-150C岩石力学试验系统。充填体的尺寸为70.7 mm×70.7 mm×70.7 mm,养护龄期为28 d。试验结果见表2。

表2 单轴抗压强度
由表2可知,在灰砂比一定时,充填体的单轴抗压强度与浓度呈正比,随浓度的增大而增大;在浓度一定时,充填体的单轴抗压强度与灰砂比呈正比,随灰砂比的增大而增大,即水泥胶结材料用量越多,强度越大。
3 料浆流变特性试验

图1 R/S+SST软固体测试仪Fig.1 R/S+SST soft solids tester
该试验应用高精度R/S+SST软固体测试仪(如图1所示)进行充填料浆的流变参数测试试验,根据试验数据得出充填料浆的剪切应力-剪切率流变曲线以及黏度-剪切率流变曲线(如图2~4所示)。
由图2~4可知,料浆黏度在剪切过程中随剪切率的增加而逐渐减小,减小到一定值时趋于稳定。因此可知,高浓度全尾砂充填料浆的流变特性可用宾汉体流变模型表示[6-8],即充填料浆剪切应力与剪切率的关系呈线性关系,公式如下:
τ=τ0+ηγ
(1)
式(1)中:τ0为屈服应力,Pa;η为黏度系数,Pa·s;
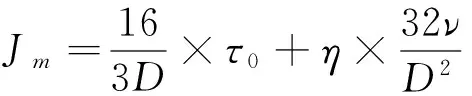
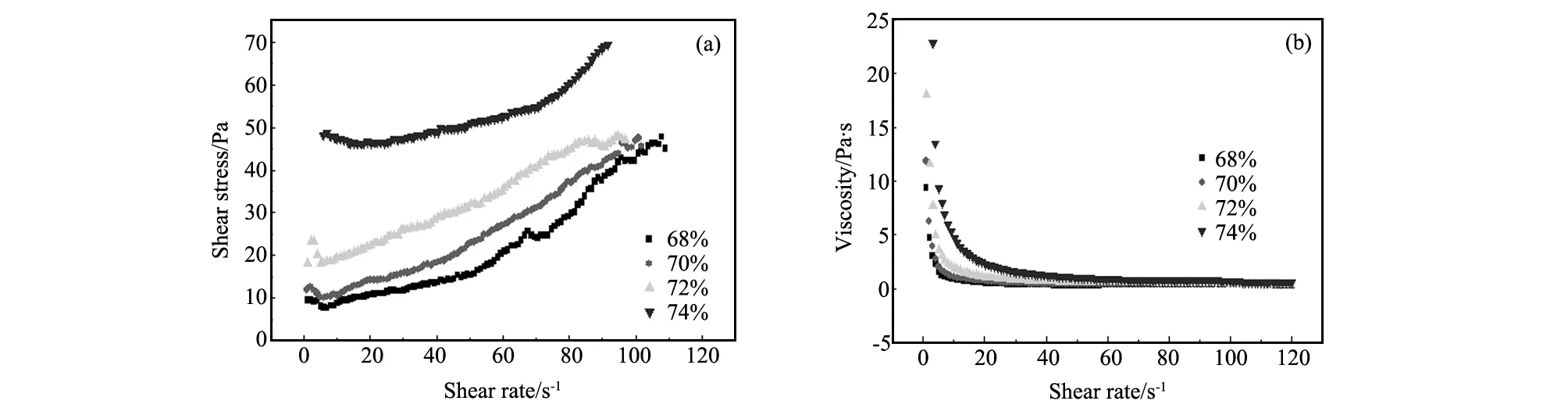
图2 灰砂比1∶8的流变试验曲线Fig.2 Flow curve of cement-sand ratio 1∶8

图3 灰砂比1∶6的流变试验曲线Fig.3 Flow curve of cement-sand ratio 1∶6
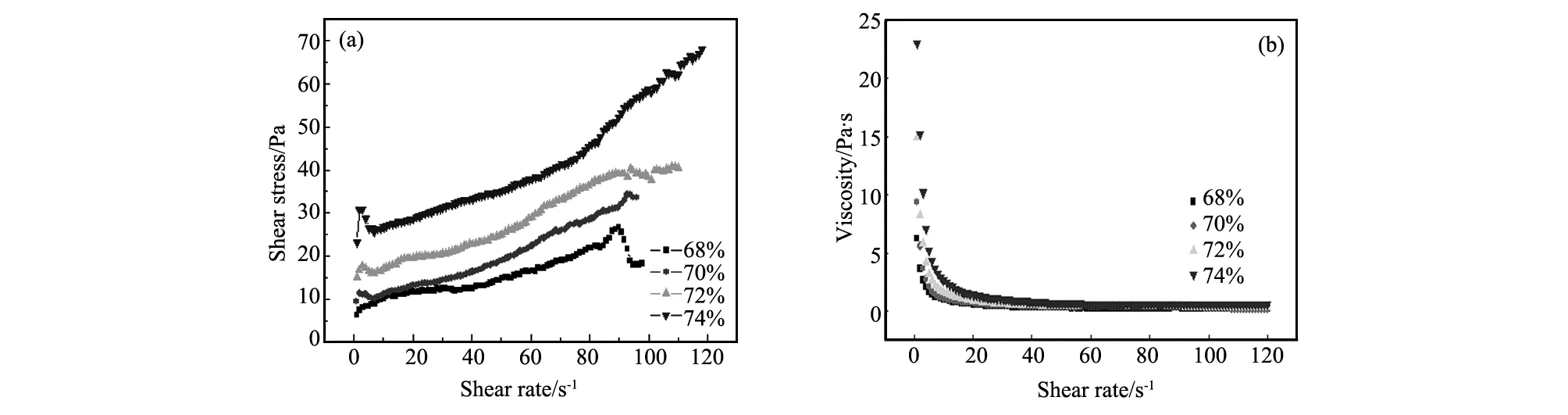
图4 灰砂比1∶4的流变试验曲线Fig.4 Flow curve of cement-sand ratio 1∶4

灰砂比1∶81∶61∶4浓度/%687072746870727468707274屈服应力/Pa1.37875.340615.899236.93932.44375.913315.008633.01573.91277.429813.779820.2259
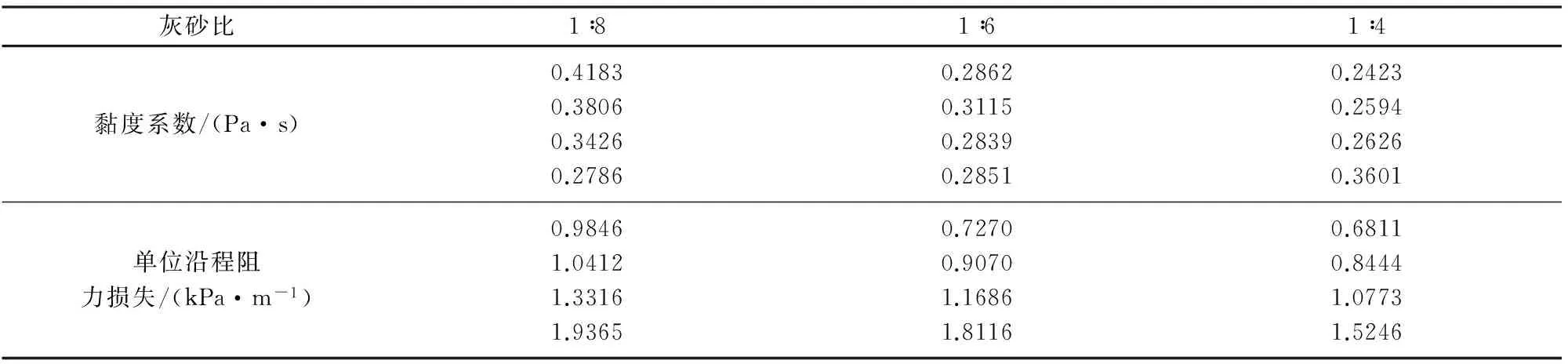
续表
由表3可知,在灰砂比一定时,充填体料浆的单位沿程阻力与浓度呈正比,料浆的浓度越大,其单位沿程阻力越大;在浓度一定时,充填体料浆的单位沿程阻力与灰砂比呈反比,料浆的灰砂比越大,其单位沿程阻力越小,即水泥胶结材料用量越多,料浆在管道输送时的单位沿程阻力越小。
4 自然沉降试验

图5 自然沉降试验Fig.5 Natural sedimentation test
为了解充填料浆自然沉降规律,对其进行了充填料浆的自然沉降试验,如图5所示。为保证试验准确,12组试验料浆的总质量保持一致,在相同的时间段测量上部清水高度,总沉降时间60 min。通过试验可知,在沉降过程中料浆上部清水高度随时间变化趋势为先直线增大后趋于平稳。其中增长的直线段斜率即为自然沉降速率[12]。其试验结果如表4所示。

表4 自然沉降试验结果
由表4可知,在灰砂比一定时,自然沉降速率与浓度的关系不呈直线关系,在浓度72%的自然沉降速率最大;在浓度一定时,自然沉降速率与灰砂比呈反比,随灰砂比的增大而减小,即水泥胶结材料用量越多,料浆的自然沉降速率越小。
5 充填料浆配比的优化
5.1模糊数学综合评判优选
模糊数学中所指的模糊现象,是指多个客观事物之中存在的区别所表现的“不明确性”,这种客观事物之间的“不明确性”,在模糊数学上称之为“模糊约束”或“模糊目标”。运用模糊数学理论和方法可以使充填配比优化的选择更具有科学性和可靠性[13,14]。
模糊数学评判模型如下:
B=A×R
(2)
式中:B-相对选择矩阵;A-各方案的权矩阵;R-模糊关系隶属度矩阵。
5.2模糊关系隶属度矩阵
首先应将各指标无量纲化,并用0~1之间的数表示,对于正指标(指标值越大充填效果越好),用式(3)计算各因素的隶属度;对于负指标(指标值越小充填效果越好),用式(4)计算各因素的隶属度。
xi为正指标时,rij=xij/ximax
(3)
xi为负指标时,rij=1-xij/ximax
(4)
式中:xij为j方案i因素的指标值;ximax为i因素的指标最大值。
灰砂比1∶8、1∶6和1∶4的各配比的因素指标,如表5所示。
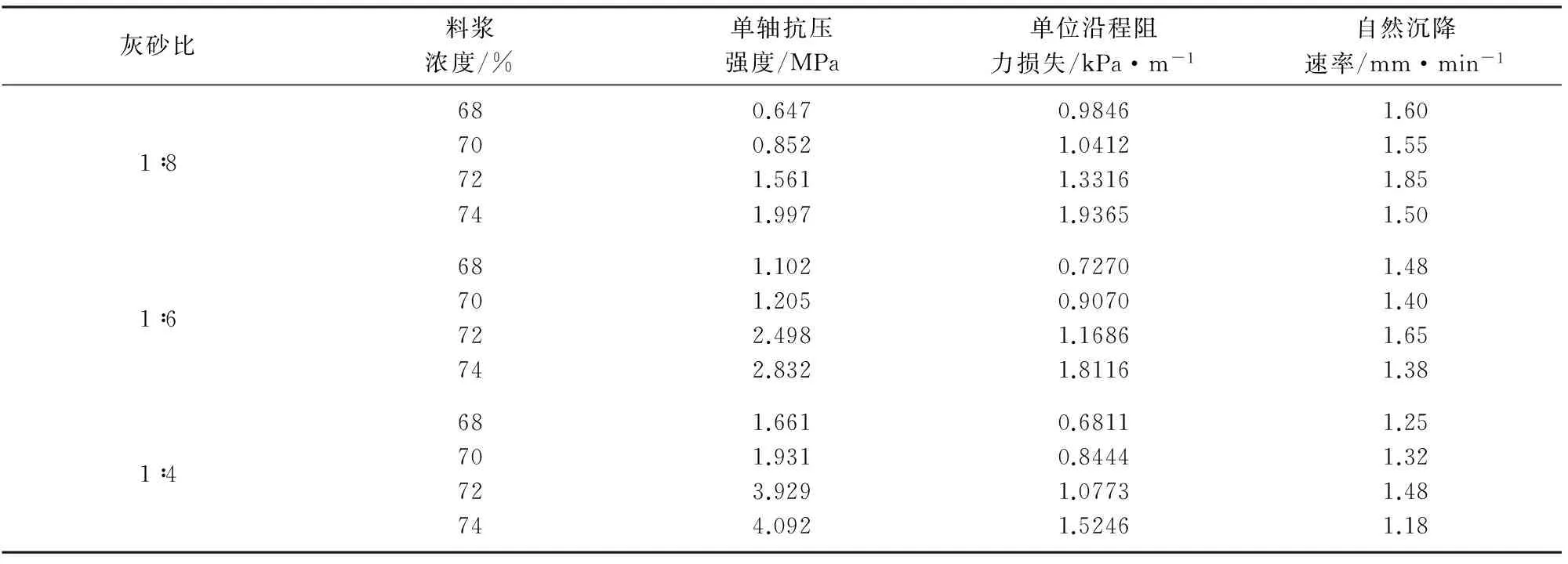
表5 各配比的因素指标
结合公式(2)和(3)计算后,得:
5.3层次分析法确定权重
根据1~9标度法,对以上三种影响因素的重要度互相进行比较。通过专家进行重要度评价,建立影响因素之间的判断矩阵,然后计算出各因素的总权重[15-18]。其判断矩阵,如表6所示。

表6 判断矩阵
用几何平均的方法计算各因素的总权重,归一化处理得各因素的总权重为:A=(0.540,0.297,0.163)。
5.4层次分析法确定权重
根据前面得到的权重分配向量和模糊评判矩阵,利用模糊数学评判模型,得到评判。
B1∶8=A×R1:8(0.462,0.504,0.678,0.672)
B1∶6=A×R1:6(0.34,0.516,0.745,0.676)
B1∶4=A×R1:4(0.93,0.533,0.768,0.670)
根据最大隶属度原则,灰砂比1∶8中选择浓度72%,即方案一;灰砂比1∶6中选择浓度72%,即方案二;灰砂比1∶4中选择浓度72%,即方案三。各方案的因素指标,如表7所示。

表7 各方案的因素指标
各方案的隶属度矩阵为:

B=A×R=(0.377,0.525,0.727)
根据最大隶属度原则,方案三为最优方案,即充填料浆的最优配比为灰砂比(水泥用量∶全尾砂用量)1∶4、浓度72%。
6 结 论
(1)在灰砂比一定时,水泥胶结全尾砂充填体的单轴抗压强度与浓度呈正比,随浓度的增大而增大;在浓度一定时,充填体的单轴抗压强度与灰砂比呈正比,随灰砂比的增大而增大,即水泥胶结材料用量越多,强度越大;
(2)在灰砂比一定时,充填体料浆的单位沿程阻力与浓度呈正比,料浆的浓度越大,其单位沿程阻力越大;在浓度一定时,充填体料浆的单位沿程阻力与灰砂比呈反比,料浆的灰砂比越大,其单位沿程阻力越小,即水泥胶结材料用量越多,料浆在管道输送时的单位沿程阻力越小;
(3)在灰砂比一定时,自然沉降速率与浓度的关系不呈直线关系,在浓度72%的自然沉降速率最大;在浓度一定时,自然沉降速率与灰砂比呈反比,随灰砂比的增大而减小,即水泥胶结材料用量越多,料浆的自然沉降速率越小;
(4)通过模糊数学结合层次分析法数据分析方法,得出该水泥胶结全尾砂充填料浆的最优配比:灰砂比(水泥用量∶全尾砂用量)1∶4、浓度72%。
[1] 刘同有,周成浦,金铭良,等.充填采矿技术与应用[M].北京:冶金工业出版社,2001:75-76,147-149.
[2] 周爱民.矿山废料胶结充填[M].北京:冶金工业出版社,2007:92-108.
[3] 谢广祥. 巷旁充填材料配比的优化选择[J]. 矿山压力与顶板管理, 1995(1): 49-52.
[4] 张钦礼,李谢平,杨伟. 基于BP网络的某矿山充填料浆配比优化[J]. 中南大学学报(自然科学版), 2013,(7):2867-2874.
[5] 王萧萧,申向东.不同掺量粉煤灰轻骨料混凝土的强度试验研究[J]. 硅酸盐通报,2011,30(01):69-73,78.
[6] 贺礼清.工程流体力学[M].北京:石油工业出版社,1998:135-160.
[7] 李元辉,孙豁然,孙凯年.新城金矿充填料流变特性研究[J].黄金,2000,(2):20-24.
[8] 杨焕文.水砂充填料浆流变参数的现场测定及应用[J].黄金,1997,(2):21-26.
[9] 陈忠熙,赵奎,许杨东,等.某矿高浓度全尾砂料浆絮凝沉降特性试验研究[J]. 有色金属科学与工程, 2015,(3): 88-93.
[10] 许毓海,许新启.高浓度(膏体)充填流变特性及自流输送参数的合理确定[J].矿冶,2004,(3):16-19.
[11] 吕宪俊,金子桥,胡术刚,等.细粒尾矿充填料浆的流变性及充填能力研究[J].金属矿山,2011,(5):32-35.
[12] Wasp E,Kenny J,Gandhi R.Solid-liquid flow slurry pipeline transportation[M].Berlin:Transport.Technology.Publications,1977:108-117.
[13] 孙兆刚. 模糊数学的产生及其哲学意蕴[D]. 武汉:武汉理工大学, 2003.
[14] 刘国. 用模糊数学方法选择软土地基加固方案[J].水文地质工程地质,2000,(4): 17-19.
[15] 王丽丽. 模糊数学法结合层次分析法用于清洁生产潜力评估研究[D]. 重庆:重庆大学,2010.
[16] 张琳,李长俊,苏欣,等.模糊层次分析法确定管线风险因素权重[J]. 石油机械, 2006,(6): 43-48.
[17] 郭金玉,张忠彬,孙庆云.层次分析法的研究与应用[J]. 中国安全科学学报, 2008,(5): 148-153.
[18] 邓雪,李家铭,曾浩健,等.层次分析法权重计算方法分析及其应用研究[J]. 数学的实践与认识, 2012,(7): 93-100.
Optimization of the Slurry Ratio in the Cemented Filling with the Cement Based on Fuzzy Mathematics and Analytic Hierarchy Process
LUOTao1,2,HEWen1,2,SHIWen-fang1,2,XUYang-dong1,2,CHENZhong-xi1,2,JIANGLiang-liang1,2
(1.Faculty of Resource and Environmental Engineering,Jiangxi University of Science and Technology,Ganzhou 341000,China;2. Jiangxi Key Laboratory of Mining Engineering,Jiangxi University of Science and Technology,Ganzhou 341000,China)
Aiming at the existing problems of backfill effect in stopping of residual ore in a mine, it was proposed to adopt cemented tailings backfill. This paper preliminarily identified Influencing factors of fill effect which were 28 d compressive strength, unit resistance along the way and natural sedimentation rate according to the flow properties and mechanical properties of the full tailings slurry. we made use of fuzzy mathematics and AHP to establish membership matrix of each ratio and weighting matrix of the above factors, to define results of the optimal ratio of the full tailings slurry that cement-sand ratio (cement quality∶full tailings quality) was 1∶4 and the concentration was 72% by fuzzy decision. The optimization indicates that the optimal ratio can effectively Improve slurry delivery performance and reduce filling cost on the premise that the strength is maintained.
compressive strength;unit resistance along the way;natural sedimentation rate;fuzzy mathematics;analytic hierarchy process
江西省科技支撑计划重点项目(20141BBG70097);江西省工业安全工程技术研究中心开放基金(2013GGY001)
罗涛(1990-),男,硕士研究生.主要从事岩石力学与工程方面的研究.
何文,博士,副教授,硕导.
TQ172
A
1001-1625(2016)07-2241-06
