基于计算机图形学的非线性投影问题研究

徐时芳

（黔南民族师范学院数学系，贵州都匀558000）

基于计算机图形学的非线性投影问题研究

徐时芳

（黔南民族师范学院数学系，贵州都匀558000）

随着科学技术的不断发展，非线性的投影方法由以前的小范围使用，发展到了包括在计算的机图形学、图像处理、地图设计、摄影，画画等领域中。为了使各需要投影技术的领域提供更好的技术支持，文中提出了计算机图形学的非线性投影问题研究，首先研究了计算机图像学以及图像处理等几个领域的非线性投影问题，包括曲面上的迭代问题，以及迭代算法，正交投影算法等。此外，还介绍了几种非线性投影。实际产生的效果表明，该方法能为投影问题提供一个全新的视角，对图形学中的非线性投影问题有着较好的借鉴意义。

正交投影；计算机图形学；球极投影；中心投影

计算机图形学中两个最重要的工具就是投影和变换由于其均可利用简单的矩阵乘法表示，因此是线性的。通常，在计算机图形学中的两个最主要的工具分别为投影和变换，又因均可被表示为简单的矩阵形式，所以称其为线性的。然而，在如今科技发展的时代，正交投影、反交投影、平行投影、全角投影、圆状投影等这些非线性投影技术，使计算机图形学得到了更好的发展，其使这一方向变得更加立体和充实，也为解决图形学问题提供了新的思路和方向［1］。

伴随着计算机图形学的发展，线性的投影问题逐渐被人们遗弃，反之非线性问题受到人们越来越大的重视，这是因不仅非线性问题有着较大的现实需要，还因其可产生更好的效果以及更大的使用空间。本文就是在此基础上，对计算机图形学中的非线性投影问题做出了深刻的研究与分析。

1　计算机图形学概述

计算机图形学，顾名思义，其是利用计算机来深入研究图形的一个学科，随着计算机技术的不断地快速发展，计算机图形学已经成为计算机大家庭中最重要的一个系统之一，且人们对此也越来越重视。之所以说计算机图像学是一个重要的分之，是因其所涉及的内容十分广泛，比如，图像处理、图像建模、3D处理、人图交互、全角投影、反交投影、还有各种图像算法模拟仿真等。研究计算机图形学的本质就是利用其来使文中所需研究的图像具有最逼真的真实感，而为了达到这一目的，则需利用几何的知识来将所需要的场景表示出来，再建立一个模型，计算出假想的光源、纹理、材质属性下的光照明效果。因此，计算机图形学与计算机的几何设计其实是密不可分的［2］。图形学在非线性投影这一方面的也起到较大作用，投影问题的研究也是计算机图像学中一个重要的研究方向，投影问题在科学上也与计算机图像学有着紧密的联系。这是因利用计算机，不仅可简单地在显示器上模拟出投影的场景，更可利用计算机来模拟和仿真各种情况下的图像的变换以及延伸。文中将介绍计算机图形学的其中一个研究方向，即计算机图形学的非线性投影问题研究，并以计算机系统为应用中心，计算机技术为基础，软硬件均可裁剪，使应用系统达到所需性能。本文用到的计算机图形系统是由专业的系统图像处理软件和常规的硬件部分组成的，这里的常规硬件就是图形处理器，还有硬件之中的输入和输出设备，其中最为重要的就是图形处理器，其之所以重要，是因其将计算机与最终得到的效果图有机结合。图形处理器还具有存储和处理图形的功能，其可使运算器的使用频率大幅降低，提高了系统的效率，且增加了显示速度［3］。如图1所示，为计算机图形学中的图像处理与图形之间的联系与转换过程，其也是图像处理中重要的过程之一。

图1　图形与图像处理之间的联系与转换

2　参数曲线在隐式曲面上的正交投影问题描述

通常，研究人员在研究参数曲线在隐式曲面上的正交投影这一问题时，分为两种方法：分别是一阶微分方程法和离散投影法，但随着计算机技术的不断发展，其缺点也逐渐显现，第一种微分方程法由于本身需要的条件较高，比如数值的个数，大小以及精度，严重影响了计算的准确性和效率。第二种离散投影法，其的步骤是先将所需的曲线利用数学知识进行离散，然后在投影到曲面上进行运算，其的一个重要问题就是忽视了曲线的几何特性且过程较为繁琐，严重影响了分析的速度，使效率大幅缩减［4］。因此，文中经过认真的分析并对之前的方法进行比较，提出了一种全新的计算曲线在隐式曲面上正交投影的算法，即二阶迭代算法。在下面的介绍中，首先对问题进行描述然后对二阶迭代算法的建立过程进行介绍，然后将此方法与之前的两种方法进行对比，说明了设计的算法在精度和效率等两个方面的改善。最终，根据所要求的目的，充分的利用两个曲面和曲线之间的数学性质，计算出正交投影点q对于参数u的一阶和二阶导数，然后使用泰勒公式迭代计算隐式曲面S上一系列点来逼近正交投影曲线，这一系列的过程最终将曲面上的各个点紧紧的联系到了一起。同时，为了使二阶迭代算法的误差能尽可能的减小，还提出了一个有效的误差校正方法。图2为参数曲线到隐式曲面的正交投影。

图2　参数曲线到隐式曲面的正交投影

2.1正交投影曲线追踪算法

在正交投影映射下，隐式曲面S上的正交投影点q与参数曲线F的参数u之间存在某种函数关系，即：q=q（u）=［XYZ］。由已知的两个投影之间的正交关系，利用数学公式进行计算，算出曲面上的正交投影点q对于参数u的一阶和二阶微分量，然后在运用柯西不等式建立一个无限接近二阶迭代的方法，目的就是与正交的投影曲线达到一致。本文通过数学运算的分析可得到，假设隐式曲面S上存在的点为q，同时向量pq=p-q与隐式曲面S在q点处的法向量F平行，因此其的乘积积等于零。随后，便可求出正交投影曲线坐标点q对于参数u的各阶导数［5-6］。结合上述公式，再利用二阶迭代算法以及矩阵的性质求出各个投影点的坐标值。这么做的优点在于，当矩阵在p和q点处不满足右可逆条件时，p为隐式曲面s在点q处的一主曲率圆圆心。在上述分析的基础上，对投影点的计算以及生成方法在做进一步研究，设计出了一种新的步长选取方法，其是基于柯西不等式以及其他数学原理为基础的。此时，出现了一个新的问题，在取点时，若用相同参数的空格来选点，则就不能完全并使参数曲线F上的点达到均匀的效果，同时参数曲面上对应的正交投影点序列的分布也无法确定，不能保证其的连贯性。所以，使用下面的方法，即分别用沿着参数曲线的恒定弧长增量v以及沿着正交投影曲线的恒定弧长L增量来控制迭代歩长，则下一个投影点就会进行自动追踪。又因上述迭代的过程中存在的高阶项舍去的问题而造成误差的积累，故必须使用一个误差的改进方法，即一阶误差校正方法，对计算出的点进行误差校正，使得校正后的投影点同时满足距离误差阈值和正交误差阈值的要求，并使二阶迭代算法的误差尽可能的减小。

2.2算法描述

下面进行算法实现，曲线到曲面上的正交投影算法是研究中最为重要的一环，其的成功与否决定着最终研究的成败，文中先计算出迭代过程中最初需要使用的数据，然后在算法的进行过程中，运用前面介绍的误差消除方法，对所得到各个点进行误差的消除，直到满足算法最终的要求，并将校正后的正交投影点作为以后投影时第一次运算的值，并一直保存，直至最终所有参数曲线投影结束为止［7］。以下是上述问题的具体算法，输入：参数曲线p隐式曲面s，点p及其在隐式曲面上的正交投影点q，距离误差阈值和正交误差阐值。输出：隐式曲面上一序列的正交投影点q。算法具体描述如图3所示。

图3　算法描述

3　算法仿真与比较

文中的仿真实验均采用曲线和曲面作为实验仿真输入数据。具体而言，对于曲线和曲面，需给出曲线的控制顶点、曲面的控制网格点、节点向量。算法在MATLAB中实现，硬件条件为2.80 GHZ CPU和1 GB内存［8］。经过仿真可看到，本文所设计的二阶算法在效率与精确性两方面相比之前的通用方法得到了大幅提高。虽该算法比起之前的方法可能更为复杂，但却对所得出的每个点同时进行了误差消除的处理，表面上看到效率有所降低，但进行仿真与模拟后，发现误差不仅大幅减少，且效率也得到了提高。而在对误差的处理过程，两种算法也不相同，我们所计算出的不仅需要确定这一点是否在隐式曲面上，同时也要确定是否与所要求的投影曲线相一致；而文中设计出的新算法所求出的点完全无需考虑这一问题，只需检验计算出正交投影点是否偏离所要求的正交投影曲线即可。另外，如曲面和全面之间，重复点或两者相交时的曲线，均具有较好地研究价值和广阔的应用前景。图4为马蹄铁形曲线在汽牢顶盖曲面上的投影。

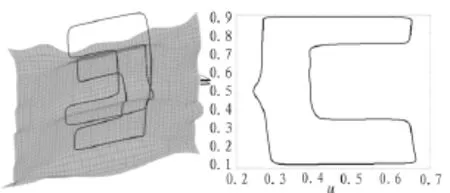
图4　马蹄铁形曲线在汽牢顶盖曲面上的投影

4　结束语

文中研究了计算机图像学以及图像处理等几个领域的非线性投影问题，也对计算机图形学做了一个概述，所研究的问题包括曲面上的迭代问题，以及迭代算法，正交投影算法等。并根据所提出的问题，进而给出了相应的解决方法如二阶迭代算法，此方法可以尽可能的减少误差，并同时提高精度及运算效率。实际产生的效果表明，该方法能给投影问题提供一个全新的视角，对计算机图形学中的非线性投影问题也有着较好的借鉴意义。

［1］徐海银，方雄兵.点到三维隐式曲线的交投影算法系统仿真学报［M］.1版.北京:清华大学出版社，2004.

［2］余正生，樊丰涛，王毅刚.点到隐式曲线曲面的最小距离［J］.工程图学学报，2005（5）:74-79.

［3］陈小雕，雍俊海，汪国昭.平面代数曲线间最近距离的计算［J］.计算机辅助设计与图形学学报，2008，20（4）:459-463.

［4］李庆扬，王能超，易大义，等.数值分析［M］.3版.武汉:华中科技大学出版社，2002.

［5］胡景生.变压器经济运行［M］.北京:中国电力出版社，1999.

［6］刘伟军，孙玉文.逆向工程——原理、方法及应用［M］.1版.北京:机械工业出版社，2000.

［7］刘玉身.离散模型光滑算法的研究［D］.北京:清华大学，2006.

［8］边柯柯，柯映林，李江雄.基于空间栅格支撑与曲率云图引导的点云表面构线［J］.机械工程学报，2009，45（8）:171-175，181.

［9］冯慧娜，白艳萍，胡红萍.一种基于图像处理和投影的车牌定位方法［J］.电子科技，20103，23（11）:5-7.

The nonlinear projection problem research based on computer graphics

XU Shi-fang
（Department of Mathematics，Qiannan Normal College，Duyun 558000，China）

With the continuous development of science and technology，nonlinear projection method by using a small scale，the development of the included in the calculation of machine graphics，image processing，map design，photography，painting，etc.To projection technology needed for various areas to provide better technical support，this paper presents a nonlinear projection of computer graphics research，we studied in the field of computer graphics and image processing，and so the nonlinear projection problem，including the iteration of curved surface，and the iterative algorithm，orthogonal projection algorithm，etc，also introduces several nonlinear projection，the effect of the actual show that the method can provide a new perspective for projection problem，nonlinear projection problem of graphics has a very good reference significance.

orthogonal projection；orthogonal projection；the ball polar projection；center of the projection

TN99

A

1674－6236（2016）12-0162-03

2015-07-01稿件编号：201507004

徐时芳（1982—），女，贵州瓮安人，硕士，讲师。研究方向：信息与计算。