双通道定位与盲分离结合的噪声分离方法
2016-10-14卓瑞岩李胜扬
卓瑞岩,向 阳,李胜扬
双通道定位与盲分离结合的噪声分离方法
卓瑞岩1,2,向阳1,2,李胜扬1,2
(1.武汉理工大学 能源与动力工程学院,武汉 430063;2.武汉理工大学 船舶动力系统运用技术交通行业重点实验室,武汉 430063)
探索双通道定位算法与盲源分离相结合进行噪声分离的可能。根据双通道空间定位理论,以声音传播过程中在双通道间产生的延时差和强度差为线索对混合信号进行分离。当待分离的辐射噪声中存在时频混叠或同一位置多个源时,双通道定位分离算法能分离出不同位置处源信号,然后利用盲源分离方法对同一位置处的多个源信号进行再分离。在Roomsim中进行分离方案的可行性验证,假设房间六个壁能100%吸收所有频率信号,不存在反射与混响,对比分析声源位置及个数对分离结果的影响。结果表明,当源位置的个数不大于3时,双通道定位分离算法能有效分离出不同位置的声源信号,用盲源分离方法可进一步分离出相同位置处的不同源信号,但当源位置个数大于等于4时双通道定位分离算法的分离性能降低。
声学;双通道定位;延时;衰减;盲源分离;噪声分离
内燃机噪声源的识别定位研究方法主要包括基于声阵列技术的噪声源识别方法和基于现代信号处理技术的噪声源识别方法[1]。声阵列技术中的波束形成可以识别表面辐射噪声源,Pengxiao Teng、Rilin Chen等用螺旋形传声器阵列技术对风力涡轮发电机主要噪声源产生部位进行了识别和可视化研究[2]。现代信号处理中的盲源分离能对混合噪声进行分离,得到单一声源。李林洁等结合EMD和ICA对内燃机噪声源进行了识别研究并进行试验验证[3]。根据计算听觉场景分析[4-5]基本理论,Scott Richard等提出双通道定位分离算法,以双通道信号间的延时差和衰减差为分离组织线索进行聚类分析,结合时频掩蔽重构出单一位置源信号,达到分离效果[6-7]。
声阵列技术能够得到声压云图,不能达到分离的目的,盲源分离技术要求源信号满足高斯性假设,且存在幅值不确定性,双通道定位分离算法不存在高斯性假设,但无法分离同一位置处的多个源。针对上述问题,本文将结合双通道定位分离算法与盲源分离算法,首先用双通道定位分离出不同位置声源信号,进一步对同一位置存在混叠的分量进行盲源分离,探索此分离方案的可行性。
1 双通道定位理论
1.1混合模型
算法假设不存在信号源反射造成的干扰,因源信号的混合方式基本满足无反射混合模型。假设有N个源信号sj(t),j=1,…,N,经过一段传播途径,被两个传声器接收的混合信号分别为x1(t)和x2(t),考虑到两个接收信号之间的衰减和延时,则无反射混合模型可表示如下

其中N是源信号数,δj为源信号Sj到达两传声器的延时,αj为源信号Sj到达两传声器时产生的相对衰减。
1.2声源定位
由傅里叶变换的时移性质有

因此,无反射混合模型转变成时频域表达式为

根据信号时频点的正交性,每个时频点上至多只有一个源信号占优。因此,对于其中某一确定的时频点(τω),混合信号可以表述为下式

根据上式,对某一时频点,双通道信号时频域的比值决定了该时频点上占优能量的衰减和延时属性,因此对每个时频点作双通道信号的比值计算
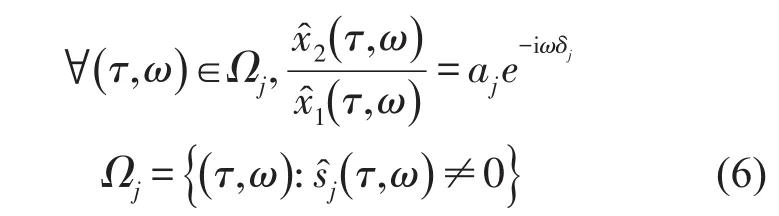
由此可以计算得到各个时频点上延时和衰减的计算公式
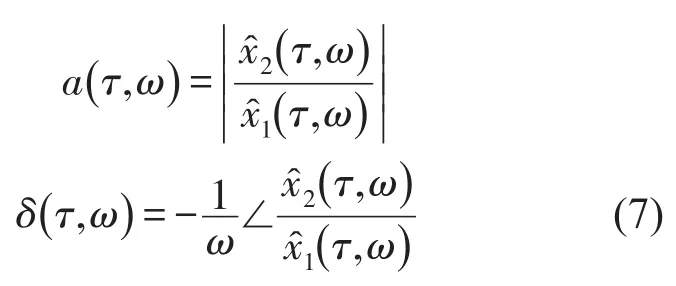
计算出混合参数对后,由最大似然估计(Maximum-Likelihood,ML)算子式得到每个时频点的加权幅值

其中,一般取p=1,q=0。且每个幅值都对应一个衰减和延时参数对,将具有相同对称衰减和延时参数对幅值进行累加,即可得到二维直方图矩阵的幅值

△α、△δ为衰减和延时分辨率宽度,I(α,δ)为属于某一声源的衰减-延时集合。声源位置与直方图中峰值坐标相对应,图1是将三个声源布置不同位置时得到的直方图,三个峰值即代表三个声源。

图1 三个不同位置处声源的衰减-延时聚类图
1.3声源分离
由于声源位置信息与衰减-延时坐标相对应,因此用时频掩蔽的方法将声源分离。以据峰值中心坐标的欧氏距离作为最大相似度,将峰值附近的时频点归为一类,使用二进制时频掩蔽将属于一类的时频点标记如下

其中αn和δn是第n个声源的衰减和延时区间。用上式将同一源信号的时频单元提取出来,再由傅里叶逆变换将提取的时频域下的源信号恢复到时域,以此达到不同位置处声源的分离目的。
综上所述,双通道定位分离算法的计算流程如表1所示。
2 盲源分离
双通道定位分离方法可将不同位置处源信号分离开来,但对同一位置存在多个源信号的情况,此处分量仍为混合信号,这就构成了欠定盲源分离问题。解决盲源分离问题的基本方法是独立分量分析(ICA),而ICA要求输入为多通道信号。因此将数据分解和ICA相结合可以解决多输入要求的难题[9]。集总经验模态分解(EEMD)根据信号本身的时频域特性,将其分解成为若干个本征模态函数和一个单调残余量,分解结果充分保留信号本身非平稳和非线性特征,具有很好的自适应性,同时可以有效抑制模态混叠现象[10]。因此,用EEMD作为ICA的数据前处理方法,具体流程见图2。

表1 双通道定位算法的计算过程

图2 EEMD+ICA分离流程图
3 可行性分析
仿真试验在Roomsim中进行,分析声源个数及声源位置(见表2)对分离效果的影响。房间尺寸设为6.25 m×3.75 m×2.5 m,六个壁面对所有声音频率具有相同的吸声系数,即六个吸声壁能100%吸收所有频率信号,不存在反射与混响。两个全指向性麦克风连线中点位于(1.6 m、1.9 m、.1 m)处,麦克风间距设为4 cm,声源处于同一正半平面的不同方位角,如图3所示。

图3 试验结构示意图

表2 声源个数及位置
3.1声源个数对分离效果的影响
经仿真试验得出,声源数目小于等于3时,双通定位分离算法可得到峰值与声源清晰对应的直方图,分离效果较为理想,而声源数目大于3时,直方图中峰值与源信号对应不明显,难以得到理想的分离结果。以3个声源(试验3)和4个声源(试验6)为例,选取相同长度语音信号作为源信号进行混合,文中所用语音信号均来自TIMIT语音库,为经归一化处理后的无量纲数据,如图4所示。

图4 源信号时域波形图
双通道定位算法对混合信号进行分离,得到图5所示直方图,其中(a)直方图清晰显示出三个峰值,对应三个源信号,而(b)直方图只有一个较为突出峰值,其他峰值不明显,无法较好分离出源信号。
其中(a)三声源分离结果中y1对应源信号S1,y2对应源信号S3,y3对应源信号S2,分离效果理想。而(b)四声结合时频掩蔽,将峰值对应源信号进行分离,结果如图6所示。

图5 不同声源数目延时衰减聚类直方图

图6 分离分量时域波形图
源分离结果中y1、y2与源信号S1、S2对应,y3、y4与S3、S4源信号差别较大。由此可见,双通道定位分离算法对于源数目大于3的混合信号分离性能较差。
3.2声源位置对分离效果的影响
试验中发现,当声源数目一定时,其所处位置对双通道定位分离性能同样存在较大影响,声源位置分布包括无声源位置重叠和有声源位置重叠两种情况。
3.2.1无声源位置重叠
以试验5、试验6为例进行对比,声源分别位于(-90°、-30°、30°、90°)和(-60°、-20°、20°、60°)处,如下图7所示,声源信号为图4(b)中所示四段语音信号。

图7 声源与麦克风位置示意图
双通道定位算法对两路混合信号进行分离,得到图8所示延时和衰减的聚类直方图。
由图8可得,当声源数目相同,而声源分布位置不相同时,所得分离结果有明显差异。试验5所得直方图存在一个主峰值和较多杂乱的小峰值,峰值个数明显大于声源个数,结合时频掩蔽无法达到分离效果。图8(b)显示出一个主峰值和三个较小峰值,结合时频掩蔽可以分离出与源数目相等的分量,分量波形如图6(b)所示,分离效果较好。
3.2.2有声源位置重叠
当同一位置存在多个声源时,双通道定位分离算法无法将这些声源分离开,需要结合盲源分离进行分离。以试验4为例,设置两个声源位于相近的空间角如S1和S2,如图9所示。

图8 不同声源位置延时聚类直方图
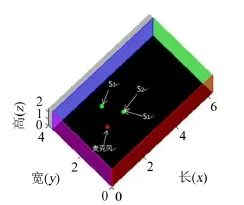
图9 声源位置混叠示意图
源信号S1、S2和S3时域波形如图10所示。
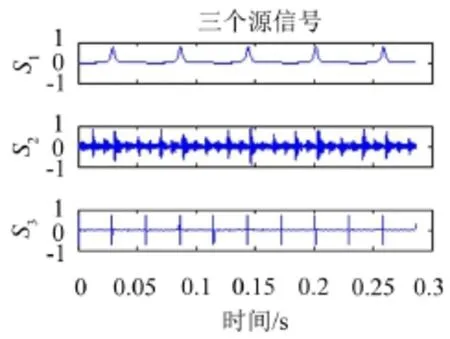
图10 源信号的时域波形
首先用双通道定位算法对两路混合信号进行分离,得到如图11的延时和衰减的聚类表示。从图中看出,由于源信号S1和S2布置在很近的空间位置,其对应的直方图峰值统计能量较大;图中仅出现两个峰值说明算法无法将三个源信号分离出来。

图11 双通道定位分离的特征聚类表示
双通道定位分离得到两个分量y1和y2,如图12所示。
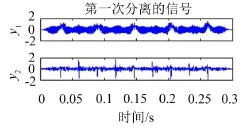
图12 双通道算法分离得到的两个分量
从定量判断的角度对信号进行包络相关分析,计算各分量与不同源信号相关系数,结合主观判断,得出分量y2对应源信号中的S3,y1是位于相近位置的S1和S2的混合信号,针对上述分离的分量y1,盲源分离方法进行分离,得到两个分量Z1和Z2,如图13所示。由于盲源分离本身存在的幅值不确定性,分离结果与源信号存在一些差异,但可以看出,分量Z1对应源信号中的S1,而分量Z2对应S2。因此,仿真分析达到了分离全部源信号的效果,也验证了前述双通道定位算法与盲源分离相结合的噪声分离方案的可行性。
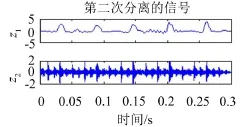
图13 盲源分离得到的两个分量
4 结语
(1)基于双通道定位理论的噪声分离方法可以分离出不同位置处声源,再借助EEMD和ICA相结合的盲源分离方法,可将同一位置处的多个源信号分离出来。
(2)当源信号数目不大于3时,双通道定位分离算法分离性能较好,算法的分离性能随着声源数目的增加而降低。源信号位置以及对混合信号进行时频分解时窗函数和频率间隔对算法性能均有影响,这是否是导致算法不适用于大于3个声源的原因以及对双通道定位分离算法的优化有待进一步探索。
[1]胡伊贤,李舜酩,张袁元,等.车辆噪声源识别方法综述[J].振动与噪声控制,2012,32(5):11-15.
[2]TENG PENG XIAO,CHEN RI LIN,YANG YI CHUN. Noise source identification applied in electric power industry using microphone arrays[J].Scientific Research Engineering,2013(5):152-156.
[3]李林洁.EMD和ICA在内燃机振声信号分析中的应用研究[D].天津:天津大学,2012.
[4]BERGMAN A S.Auditory scene analysis:The peceptual organization of sound[M].Boston:The MIT Press,1990.
[5]WANG D L,BROWN G J.Computational auditory scene analysis:principles,algorithms,andapplications[M]. Wiley-IEEE PRESS,Hoboken,N J,2006.
[6]SCOTT RICKARD.The DUET blind source separation algorithm[M].BlindSpeechSeparation,Springer Netherlands,2007:217-241.
[7]ALEXANDER JOURJINE,SCOTT RICKARD,OZGIIR YZLMAZ.Blind separation of disjoint orthogonal signals:demixing n sources from 2 mixtures[J].IEEE,2000:2985-2988.
[8]付宁,曹离然,彭喜元,等.基于局部峰值方差检测的改进DUET算法研究[J].电子测量与仪器学报,2010,24(5):437-442.
[9]谷千伟,金炜东,余志斌.基于EEMD和ICA的单通道列车信号盲分离[J].计算机应用研究,2014,31(5):1551-1553.
[10]郑旭,郝志勇,金阳,等.基于EEMD与广义S变换的内燃机噪声源识别研究[J].内燃机工程,2011,32(5):68-73.
Noise Separation Based on Dual-channel Source Localization and Blind Source Separation
ZHUO Rui-yan1,2,XIANGYang1,2,LI Sheng-yang1,2
(1.School of Energy and Power Engineering,Wuhan University of Technology,Wuhan 430063,China;2.Key Laboratory of Marine Power Engineering and Technology,Ministry of Communications,Wuhan 430063,China)
The noise source identification based on dual-channel localization algorithm and blind source separation(BSS)is studied.According to the principle of the dual-channel localization algorithm,the noise sources in different places can be separated based on time-delay difference and intensity difference between the two channels in sound propagation process.When the radiation noise has a time-frequency overlap or multiple excitation sources appear in a same place,the dual-channel localization algorithm can separate the source signals in different places.Then,the BSS method is adopted to re-separate the multiple source signals at the same place.Finally,the feasibility of this method is verified in Roomsim,and the influence of source number and location on separation performance is analyzed.The results show that the separation method combining the dual-channel localization algorithm with BSS can separate the sources efficiently and is independent of the noise from the other positions.However,the dual-channel localization algorithm does not work well when the source number is larger than 3.
acoustics;dual-channel localization;time-delay difference;intensity difference;blind source separation(BSS);noise separation
TK421+.6
ADOI编码:10.3969/j.issn.1006-1335.2016.03.028
1006-1355(2016)03-0137-05+163
2015-12-29
国家自然科学基金资助项目(51279148)
卓瑞岩(1990-),男,河南省新乡市人,硕士研究生,主要研究方向为噪声控制、数字信号处理。E-mail:15516585566@163.com
向阳(1962-),女,博士,教授,博士生导师,主要研究方向为振动噪声分析与控制、动力机械状态检测与故障诊断。E-mail:yxiang@whut.edu.cn
