STAP抗混响辅助样本的选取方法

赵申东, 周田宰, 沈建森



STAP抗混响辅助样本的选取方法

赵申东, 周田宰, 沈建森

(海军航空工程学院青岛校区, 山东青岛, 266041)

空时自适应处理(STAP)的一个关键问题是协方差矩阵的估计, 协方差矩阵的估计是依靠待检数据附近的辅助样本来完成的。要使估计精度足够高, 就要求获取足够多的独立同分布的辅助样本。文中对混响数据辅助样本的相关性、同分布特性、时间点数选择问题进行了分析, 根据水声信号的特点, 给出了有效的处理方案。通过综合考虑协方差矩阵估计精度、自适应处理运算量和降维STAP方法等因素, 给出了采用STAP方法抑制混响时辅助样本的选取方法, 为STAP抗混响的实现提供了条件。

水声信号; 抗混响; 空时自适应处理(STAP); 辅助样本

0 引言

空时自适应处理(space time adaptive processing, STAP)是抑制机载雷达杂波的一种有效方法。Klemm[1]分析了声呐混响和雷达杂波的相似性, 指出可以采用空时自适应滤波器进行混响的抑制; Jaffer[2]设计了将STAP用于混响抑制的方案; 文献[3]提出采用梳状谱信号用来改善探测的时域分辨能力, 同时还提出了先时后空的级联自适应处理方法用来抑制混响; 文献[4]提出的方法也可视为一种广义的STAP, 以被动方式确定目标的方位; 文献[5]将STAP方法应用到拖线阵上, 给出了STAP方法的基本结构, 介绍了全维STAP方法; Pillai[6]等将STAP算法应用到了被动声呐中, 在空间-频率域内采用宽带STAP方法用来增强声呐对弱运动目标的检测能力。进行STAP处理的一个关键问题就是待检数据混响协方差矩阵的估计, 而这一估计依靠的是合理选取辅助样本, 即选择足够多的满足独立同分布条件的辅助样本。以上研究表明, STAP用于混响抑制可取得明显效果, 但均未对协方差矩阵求解方法和标准进行详细讨论。文献[7]针对协方差矩阵的影响进行了专门研究, 比较了理论导向矢量合成法和直接阵列数据域法2种协方差矩阵计算方法。文章将讨论解决如何从混响序列中合理选取辅助样本这一问题。

1 辅助样本的相关性

所选择的辅助样本要满足独立同分布的条件。辅助样本是通过从待检数据两侧邻近的混响数据中选择与待检样本同样大小的一段空时数据而形成的, 即它们的空间采样点和时间采样点都是相同的。如何确定辅助样本的起始位置是保证样本间独立性的关键所在。仿真以及试验数据表明, 混响数据的瞬时值服从高斯分布[8], 所以辅助样本间的独立性与不相关是等价的。为此, 可以通过对2个具有一定间隔的辅助样本之间的相关性检验来判断其是否独立。

图1所示的是一组采用典型参数仿真的混响辅助样本的相关系数, 其中图(a)为脉宽50 ms的情形, 图(b)为脉宽100 ms的情形。仿真时采用由12个阵元组成的等距线阵, 阵元间隔为半波长, 基阵的运动速度为40 kn, 线阵轴线方向与基阵运动方向垂直, 即为前视阵情形; 发射信号为20 kHz的单频信号, 脉宽分别为50 ms和100 ms, 发射波束水平宽度为90°, 主波束指向线阵的法线方向, 即基阵运动的方向; 海深为50 m, 阵列距海底43.5 m, 底质为粘土; 不考虑阵元误差。

为了尽量减少混响的时间采样点数以降低STAP的处理维数, 需要对混响信号进行降采样处理。通常单频脉冲的声呐混响为窄带信号, 首先将其解调得到复包络, 然后采用较低的采样率对信号进行重新采样, 新的采样率应能保证所有可能出现的混响和目标信号的频移不会出现模糊, 在此基础上尽量采用低的采样率。本仿真的混响复包络信号采样率为1 200 Hz, 该采样率可以保证不同方位的混响频移不发生混叠, 所以脉宽为50 ms时, 目标的信号包含60个左右的采样点, 脉宽为100 ms时, 目标的信号包含120个左右的采样点。图中不同曲线表示选择不同点数时辅助样本的相关系数, 横坐标表示2个辅助样本相隔的点数。

通过图1可以看出, 当2个辅助样本相隔较近时, 它们具有较强的相关性, 当辅助样本时间采样间隔点数增加到6~7个时, 不论样本的时间点数多于还是少于发射脉宽对应的采样点数, 其相关系数基本已经降到了0.3以下, 可以认为2个辅助样本已经不相关。如果所选的时间采样间隔点数太少, 辅助样本间具有一定的相关性, 进行协方差估计时要想达到同样的精度, 就需要更多的样本数。

同时还可以发现, 当发射脉宽不一样, 而其他条件相同时, 图1(a), (b)两图中相关系数是稍有区别的, 脉宽为100 ms的相关系数要稍大于脉宽为50 ms的相关系数。这是因为发射脉宽增大后, 所有混响散射元的散射信号都会相应拖长, 总的混响时间相关性增强, 所以相同间隔的2个辅助样本相关性也会相应增强。所以, 在给定的混响序列中, 只要2个辅助样本间隔足够大, 就可以认为它们是相互独立的。当然, 样本间隔太大也是不可取的, 因为那样会使得从相同长度的混响中取得的辅助样本数量变少, 不利于协方差矩阵的准确估计。通过仿真计算, 可以得出如下结论: 2个辅助样本的相关系数降至0.3左右时, 此时2个样本的间隔点数是比较合适的选择。

2 辅助样本的同分布问题

在估计协方差矩阵时, 如果辅助样本不是同分布的, 或者说它们的统计特性是明显不同的, 那么即使独立的样本数再多也不能准确反映出混响的分布特性, 也就难以求解出有效的加权系数, 所以辅助样本的同分布是STAP协方差矩阵估计中一个重要条件。

文献[9]提出了一种采用关联维数的大小来评判样本间数据是否相似的方法。样本关联维数的差别表明了样本的相似程度或逼近程度, 2个样本的统计特性越相似, 它们的关联维数也就越接近, 可以用样本的关联维数作为剔除非均匀辅助样本的依据。关联维数的求取方法如下。

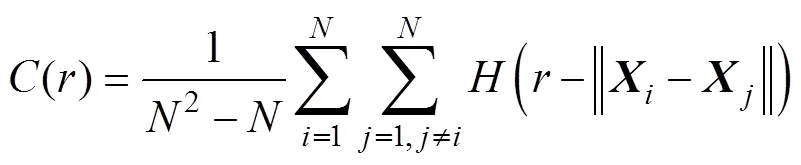
(3)

图2给出的就是位于不同时刻的仿真混响辅助样本的关联维数。仿真时, 发射信号脉宽为100 ms, 采样率为1200Hz, 辅助样本的时间采样点数为120, 其他参数与图1中的参数一样。

从图2可以看出, 不同时刻的辅助样本关联维数总体变化趋势是在逐渐增大, 这说明在短时间内辅助样本的统计特性是相近的, 而在较长时间内其统计特性逐渐发生了变化, 偏离了同分布的条件。所以, 如何选择合适的混响时间长度就成了问题的关键所在。

合适的长度应该使得所选的混响既能保证样本的统计特性不发生较大变化, 又能提供足够的样本用来进行协方差矩阵的估计。但是, 从图中还可以看出, 这些样本的关联维数存在较大的起伏振荡, 难以据此准确界定混响非均匀的范围, 所以需要依据其他的标准进行判定。实际上, 选择接收信号的功率作为均匀混响范围的判定标准是比较合适的。这是因为在平坦的浅海条件下, 混响的主要来源是海底, 不同时刻海底的散射元都是呈圆环形分布, 散射元分布情况是相似的, 所以不同时刻混响谱在空时2D平面上的分布也是相似的, 主要的差别就是混响功率与噪声功率比值的大小发生变化, 而这一变化就意味着辅助样本的统计特性发生了变化。噪声功率在整个接收过程中基本是不变的, 所以接收信号功率的变化就体现了混响功率的变化, 同样也体现出了辅助样本统计特性的变化。结合混响的衰减规律, 这里选择功率衰减在6 dB~10 dB以内的信号作为辅助样本的选取范围。

尽管这样选取的混响辅助样本并非严格满足同分布的条件, 但为了取得足够数量的辅助样本, 就不得不放松对该条件的要求, 在统计特性和混响长度上进行适当折衷。在距离较近的混响处, 由于混响衰减较快, 为了得到足够的样本数量, 可以将起止混响的功率差选为10 dB, 这样在10 kHz~20 kHz范围内, 在750 m附近的混响用于估计协方差矩阵的数据时间长度约为0.4 s; 在距离较远的混响处, 混响衰减较慢, 可以将起止混响的功率差选为6 dB, 这样在1500 m附近用于估计协方差矩阵的混响时间长度约为1 s。

3 辅助样本时间采样点数的确定

选定均匀混响的分布范围和相邻辅助样本的间隔后, 还需要确定单个辅助样本中的时间采样点数才能最终给出所有用于协方差矩阵估计的辅助样本。单个辅助样本时间采样点数越少, 则进行STAP处理的维数就越低, 运算量也就越小。但是, 较少的采样点数也会带来不利的影响。辅助样本的大小与待检数据的大小相一致, 减少辅助样本的时间采样点数也就意味着减少了待检样本的时间点数, 这首先会降低STAP处理器的频率分辨率。除此以外, 时间采样点数太少也不利于提高输出信号的信混比, 下面的仿真就说明了这一点。

图3给出的是辅助样本选用不同的时间点数时, STAP处理器的改善因子。仿真时, 发射信号脉宽为50 ms, 采样率为1200 Hz, 所以1个脉宽对应的信号时间采样点数为60, 其他参数与图1中的参数一样。图中所求的改善因子都是假设目标位于基阵运动的正前方, 即主波束照射的方向, 目标的运动速度为5 kn, 运动方向远离基阵。待检数据位于脉冲发射后的2.2 s处, 用于估计协方差矩阵的混响位于待检数据的左右两侧, 两侧的时间长度各取为0.5 s, 相邻辅助样本的时间点数为5。通过如上参数可以大概估计出所能得到的辅助样本的数量, 当单个辅助样本时间点数从10增加到100时, 辅助样本的数量从238个降到202个。可以发现, 这些辅助样本不能全部满足进行全维STAP处理的条件, 但是都可以采用一种降维的处理方法进行计算—局域联合处理(joint- domain localized, JDL)[10]。

在采用JDL方法进行处理时, 方位方向取5个辅助波束, 多普勒方向取5个辅助波束, 降维后的系统自由度为25。观察图中的改善因子可以发现, 在少于1个脉宽对应的点数60时, 随着辅助样本时间点数的增加, 处理器的改善因子随之增加。这是因为待检数据时间点数越多, 说明利用的目标回波越充分, 检测输出中目标信号的强度也就越大。但是当辅助样本时间点数超过1个脉宽所对应的点数时, 改善因子反而随着时间点数的增加而降低。这是因为点目标的信号信息已经被全部利用, 此时再增加时间点数, 反而会增加混响能量的输出, 降低了输出信混比。所以, 选择辅助样本的时间点数时, 应该在辅助样本数量能够满足协方差矩阵估计精度的前提下, 选取与发射脉宽相一致的时间点数。

4 结束语

综上所述, 混响辅助样本的选取需要兼顾样本长度、统计特性和样本数量, 而这些参数又是相互影响、相互制约的。当采用STAP方法进行混响抑制时, 需要对这几个参数进行综合的权衡折中, 同时还要考虑尽量降低系统的运算量。

通常当2个辅助样本的相关系数降至0.3左右时, 可以认为此时样本已经满足独立性的要求; 选择混响信号的功率作为均匀混响范围的判定标准是比较合理可行的一种方案; 辅助样本时间点数的选择需要考虑样本数量能否满足协方差矩阵估计的要求, 若能够保证, 则应选取与发射脉宽相一致的时间点数, 否则应该根据辅助样本的实际数量来降低样本的时间点数。

需要指出的是, 文中判断辅助样本独立性的相关系数是在特定海洋环境及发射参数下给出的, 当参数改变后, 相关系数的取值也应略有不同, 需要进行进一步的研究。

[1] Klemm R. Interrelations Between Matched-field Processing and Airborne MTI Radar[J]. IEEE Journal of Oceanic Engineering, 1993, 18(3): 168-180.

[2] Jaffer A G. Constrained Partially Adaptive Space-time Processing for Clutter Suppression[C]//28th Asilomar Conference on Signal, System and Computer, Pacific Grove, CA, 1994: 671-676.

[3] Mio K, Chocheyras Y, Doisy Y. Space Time Adaptive Processing for Low Frequency Sonar[C]//Oceans Conference Record (IEEE), USA, 2000: 1315-1319.

[4] Kim B C, Lu I T. High Resolution Broadband Beamforming Based on the MVDR Method[C]//IEEE Oceans Conference, 2000: 1025-1028.

[5] Maiwald D, Benen S, Hostermann H, et al. Space-time Adaptive Processing for Active Towed Array Sonar Systems[C]//UDT Europe 2001, 2001: 1-6.

[6] Pillai S U, Guerci J R, Pillai S R. Wideband STAP (WB- STAP) for Passive Sonar[C]//Oceans 2003. Proceedings, 2003: 2814-2818.

[7] 吕维, 王志杰, 李建辰, 等. 混响空时协方差矩阵的两种计算方法比较与分析[J]. 鱼雷技术, 2012, 20(4): 251-255.Lü Wei, Wang Zhi-jie, Li Jian-chen, et al. Comparison and Analysis of Two Calculation Methods of Space Time Co- variance Matrix for Reverberation[J]. Torpedo Technology, 2012, 20(4): 251-255.

[8] 赵申东, 唐劲松, 蔡志明. 多通道运动声呐混响仿真[J]. 舰船科学技术, 2007, 29(4): 117-120.Zhao Shen-dong, Tang Jin-song, Cai Zhi-ming. Simulation of Multi-channel Moving Sonar Reverberation[J]. Ship Science and Technology, 2007, 29(4): 117-120.

[9] 陈建文, 王永良, 皇甫堪, 等. 基于非均匀检测的机载雷达空时自适应处理方法[J]. 数据采集与处理, 2000, 15(1): 44-47.Chen Jian-wen, Wang Yong-liang, Huang Fu-kan, et al. The STAP Method of Airboarn Radar Based on Inhomogeneous Detection[J]. Data Acquisition and Processing, 2000, 15(1): 44-47.

[10] Wang H, Cai L. On Adaptive Spatial-temporal Processing for Airborne Surveillance Radar Systems[J]. IEEE Trans. AES, 1994, 30(3): 660-670.

(责任编辑: 陈 曦)

Selection of Auxiliary Samples for Reverberation Suppression via STAP

ZHAO Shen-dongZHOU Tian-zaiSHEN Jian-sen

(Qingdao Branch, Naval Aeronautical and Astronautical University, Qingdao 266041, China)

A key link in space-time adaptive processing (STAP) is the estimation of covariance matrix, which depends on auxiliary samples near the sample to be detected. To ensure the estimation accuracy, sufficient independent identically distributed auxiliary samples are necessary. In this paper, the correlation of reverberation auxiliary samples, the identical distribution characteristic, and the selection of time point number are analyzed, and a corresponding valid scheme is given according to the characteristics of acoustic signal. As a result, a selection method of auxiliary samples for reverberation suppression via STAP is proposed through comprehensively considering the estimation precision of covariance matrix, the operand of adaptive processing, and the dimension-reduced STAP.

acoustic signal; reverberation suppression; space-time adaptive processing(STAP); auxiliary sample

10.11993/j.issn.1673-1948.2016.06.004

TJ630.3; TN911.2

A

1673-1948(2016)06-0417-05

2016-08-26;

2016-10-27.

赵申东(1978-), 男, 副教授, 主要研究方向为水声信号处理.