基于M/M/1排队系统的三值光学计算机任务服务模型

王先超，张　冕，王春生，姚云飞

（阜阳师范学院 数学与统计学院，安徽 阜阳 236037）

基于M/M/1排队系统的三值光学计算机任务服务模型

王先超，张冕，王春生，姚云飞

（阜阳师范学院 数学与统计学院，安徽 阜阳 236037）

确保QoS是三值光学计算机在商业上成功的关键因素。在分析三值光学计算机任务管理系统各模块的基础上，基于M/M/1排队系统和串联队列以及先到先服务策略建立其服务模型。用系统平均响应时间分析和评价三值光学计算机性能。研究结果发现平均响应时间随任务到达率和运算量的增加而增加，随网络传输率的增加而减少；运算量和网络传输速度是影响系统平均响应时间的瓶颈。因此，提出的模型对实用的三值光学计算机任务管理系统的设计具有指导意义。

M/M/1排队系统；三值光学计算机；任务调度；响应时间；串联队列

自三值光学计算机（Ternary Optical Computer，TOC）体系结构和原理［1-2］提出后，软硬件方面的研究均取得了许多重要成果［3-17］。例如提出了降值设计理论［3］、加法器进位直达通道理论［4］，实现了无进位加法［6-8，18］和向量矩阵乘法［18］，设计并实现了TOC任务管理系统软件模块结构［12-13］，提出了相应的任务调度算法［17］和处理器分配算法［15，17］，等等。特别值得一提的是，降值设计理论使TOC的光学处理器具有重构性。也是就说，TOC具有计算的灵活性，能够根据计算需求构建不同的处理器。同时，光计算的并行性使得TOC处理器具有巨位性。总之，TOC作为一种新型计算资源，用户可以通过网络获取具有高性能、可扩展性和安全性的服务。

TOC光学处理器虽然因具备并行性、巨位性、可重构性和按位可分配性等的优良特性而吸引了众多研究者，并取得可喜研究成果，但是离TOC实用尚有很长的路要走。目前缺少对TOC系统性能的研究。为此，本文拟基于M/M/1排队系统研究TOC的服务性能，以确保其提供更好的QoS。

1相关工作

1.1TOC任务管理系统

TOC的计算模式如图1所示。在该模型中，Server是完成用户计算需求的唯一节点。用户可以通过Client和Network向TOC的Server提交任务即运算请求，完成运算后Server再将结果反馈给Client。

图1　TOC计算模式

图2给出了TOC任务管理系统中Server的模块结构图。Server的运算请求接收模块（Request Accepting Module，RAM）接收到用户提交的运算请求后，将其发送至数据预处理模块（Data PreProcessing Module，DPPM）；数据预处理模块计算运算请求的优先级并将其插入待调度链表；任务调度模块（Task Scheduling Module，TSM）完成链表中任务的调度，将任务发送到TOC；处理器分配模块（Processor Allocating Module，PAM）根据按需分配原则为已被调度的任务中的不同运算（假设不超过15个）分配光学处理器资源；同时，TOC的处理器硬件重构模块（Processor Reconfiguring Module，PRM）根据用户不同的计算需求完成光学处理器重构，TOC运用重构好的处理器模块（Optical Processor Module，OPM）为用户完成运算，解码器模块（Decoding Module，DM）对运算结果进行解码，并将运算结果发送至运算结果发送模块（Result Transmitting Module，RTM）。最后RTM模块将运算结果反馈至相应的Client。

1.2排队系统

排队论主要研究受随机因素影响而出现排队现象的系统，广泛应用于通信、交通、公共服务事业、管理运筹和计算机等领域。

近年来，许多研究者利用排队论研究云计算［19-22］。Khazaei等利用连续时间Markov链通过任务拒绝概率和平均响应延迟来研究云计算的性能［19］；Vilaplana等利用M/M/1排队系统通过响应时间来研究基于开放Jackson网络的云计算QoS［20］。虽然TOC的QoS指标涉及系统平均响应时间（为简便起见，我们称系统平均响应时间为响应时间）、吞吐量和资源利用率等，但本文拟用M/M/1排队系统研究TOC的响应时间。

图2　TOC任务管理系统模块结构图

2　基于M/M/1排队系统的TOC服务模型

2.1TOC服务模型

我们将基于M/M/1排队系统和先到先服务（First Come First Served，FCFS）策略建立TOC服务模型以分析响应时间。

Server中有唯一的一个运算请求接收模块RAM，用于接收用户的包含若干个二元三值逻辑运算的运算请求。为减少传输数据量，每个运算的操作数以通信内码（每个操作数占2个二进制位）方式传输至RAM［17］，即每个字节存放2对操作数。因为不同用户可以并发提交运算请求，不同运算请求到达时将按等待制进行排队，因此RAM可以用一个M/M/1排队系统来表达。我们以一位二元三值逻辑运算作为运算量的计数单位，假设n个运算请求到达服从参数为λ的指数分布，各运算请求的平均运算量为μ、接收运算请求的网络传输速度为ω，则传输数据量为μ/2，传输数据所需平均时间为μ/2ω，单位时间内接收运算请求个数即RAM模块的服务速率为2ω/μ。也就是说，接收运算请求时RAM的服务服从参数为2ω/μ的指数分布。

RAM接收完运算请求后，DPPM便对其进行预处理。数据预处理模块DPPM在Server中也是唯一的。也就是说，DPPM也可以用一个M/M/ 1排队系统来表达。设DPPM对运算请求中的数据进行预处理的速度为τ，则类似地可知DPPM服从参数为τ/μ的指数分布。

显然，Server中存在唯一的一个任务调度模块RSM。虽然已提出适合TOC的定时调度策略，该策略可以使光学处理器同时处理多个运算请求，但为简便起见，假设每次只处理一个运算请求，即TOC每处理完一个任务后，RSM就调度一个任务至TOC（每次调度多个任务的情况的性能分析比较复杂，我们将另行讨论）。称该调度策略为运算完成时调度策略，简称为完成时调度策略。

处理器分配模块PAM根据任务中各运算的运算量，为各运算进行按需分配光学处理器已确保各运算同时完成，并查找各运算所需光学处理器的重构码，而后将其发送至TOC的处理器重构模块PRM。因为每个运算请求中所包含的不同运算都不超过15个，发送至PRM的重构信息量变化不大。为此，假设PAM完成处理器分配所需时间为一常数。

PRM接收到处理器分配结果和各运算所需光学处理器的重构码后便进行处理器的重构，各运算器的重构是并行的，因此对给定的光学处理器，其重构所花时间也是一常数。

完成处理器重构后TOC光学处理器对数据进行运算，解码器对运算结果进行解码，并把运算结果发送至结果发送模块RTM。显然，TOC的运算时间与运算量μ和光学处理器运算速度有关。

因网络传输速度远小于光学处理器的处理速度，所以RTM模块也可以用一个M/M/1排队系统表达。因为对二元三值逻辑运算而言，两个操作数得到一个运算结果，所以运算结果的大小为μ/4。显然，发送运算结果的速度也为网络传输速度ω。因此RTM的服务服从参数为4ω/μ的指数分布。

从上述分析可以看出，上述各过程构成了一个4阶段串联排队系统［23］，如图3所示。

图3　TOC任务排队模型

根据上面的分析，TOC为n个运算请求提供计算服务的响应时间T可由下面公式计算。

其中TRA表示RAM接收运算请求所需的平均时间，TDPP表示对运算请求进行预处理所需的平均时间，TRS表示调度任务所需的平均时间，TRT表示将运算结果发送给用户的平均时间。

2.2TRA的计算

RAM可用等待制M/M/1排队系统对其建模，由文献［23，24］可知该模块接收运算请求的平均响应时间TRA可由下面的公式（2）求得。

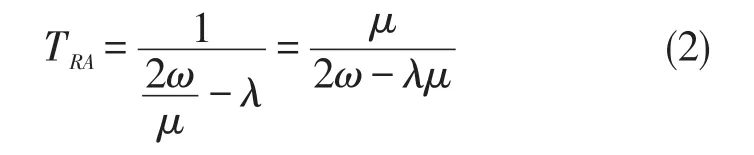
其中λ表示单位时间内到达的任务数即运算请求的到达速率，μ表示任务的运算量即传输数据大小，ω表示接收数据的平均速度。

2.3TDPP的计算

由文献［24］可知，运算请求经RAM到达DPPM的速率也是λ。由前面的分析可知，DPPM同样可用等待制M/M/1排队系统对其建模。类似地，可以得到该模块的平均响应时间TDPP。

其中τ表示DPPM对运算请求中的数据进行预处理速度。

2.4TRS的计算

RSM进行任务调度时要将一个待计算运算请求中的数据发送至TOC，并将其从队列中删除。而后PAM为其进行光学处理器分配，PRM为其进行光学处理器重构，OPM进行光运算，DM对运算结果进行解码。换句话说，RSM、PAM、PRM、OPM和DM等5个模块组合在一起可用等待制M/M/1排队系统对其建模。因此，TRS不但包括任务调度时间，还包括处理器分配时间、处理器重构时间、运算时间和解码时间。

如前所述，PAM进行处理器分配和PRM进行运算器重构所需时间都是一个常数。特别值得一提的是，处理器重构模块PRM是TOC所特有的。该模块虽然使TOC具有了计算的灵活性，但也增加了系统开销。因此，为了分析这两个模块对系统性能特别是平均响应时间的影响，虽是常数，但也不能将其忽略。

如前所述，图2中TOC模块从RSM接收到数据待完成光学处理器重构后便对其进行运算，而后DM对其进行解码。显然，TOC的处理速度为OPM速度和DM速度的较小者。

根据上述分析，假设RSM将数据发送至TOC的平均传输速率为φ，PAM完成处理器分配时间为常数C1，PRM完成光学处理器重构的时间为常数C2，TOC的处理速度为δ，则上述5个模块RSM、PAM、PRM、OPM和DM构成的等待制队列的服务速率π可由下面的式（4）求得。

类似地，可由下面的公式（5）计算TRS。

2.5TRT的计算

运算结果被发送至RTM，再被发送至相应的Client。根据前面的分析和图3，类似地可得到TRT的计算公式如下：

将（2）、（3）、（5）和（6）式代入（1）式得到基于M/ M/1排队系统的系统总体平均响应时间T。

3　模型仿真

为了研究不同参数对系统性能特别是响应时间T的影响，我们对模型进行仿真。相关参数如下：

任务到达速率λ：即单位时间内到达的任务数。由（7）式可知T是λ的增函数。

运算量μ：虽然TOC可进行无进位加法和向量矩阵乘法，但这里的运算量μ只表示各运算请求所包含二元三值逻辑运算的运算量。因为其他运算可通过二元三值逻辑运算来实现，且目前的任务管理系统中用户的Client也只能提交二元三值逻辑运算，不能提交非二元三值逻辑运算［13，18］。

网络传输速度ω：在局域网和广域网中网络传输速度相差很大，TOC不但面向局域网用户，还有很多广域网用户。因此，我们用广域网中数据传输速度对ω进行模型仿真。

数据预处理速度τ：DPPM的功能主要是根据不同的运算将通信内码表示的数据转换成用控制内码表示［17］。显然，τ与电子计算机运行速度相关，可达到G量级。

本地数据传输速度φ：TOC通过网线与Server相连以完成其间的通信。因此，φ即局域网的数据传输速度。

TOC运算速度δ：TOC的运算速度目前主要因资金的限制而受限于液晶，但考虑到其并行性，其运算速度仍可达到G量级。

为搞清λ如何影响响应时间T，用每小时到达的任务数进行模型仿真。运算量μ和网络传输速度ω的单位分别/为MB和MB/s，则RAM的服务速率为7 200ω/μ，即每小时能处理7 200ω/μ个运算请求。也就是说，ρ由ω，τ，φ和δ中的最小者确定。一般而言，ω为其最小者。当ρ＜1时，系统会达到平衡状态。当参数 μ=100，ω=2，τ=2，φ=50 和δ=1，且系统达到平衡时，对不同的λ响应时间T随λ的变化如图4所示。可看出，当每小时有一个运算请求到达时系统响应时间约为38 s，虽用多个M/M/1排队系统进行串联建模，但当任务数增加时，响应时间并非按任务数成倍增加。其原因在于虽然每个任务都要经历模型的每个阶段，但当同时存在多个任务时各模块并行工作。

图4　响应时间T随λ的变化

图5　参数变化时系统响应时间T随λ的变化

当运算量 μ=50，或ω=4而其他参数不变时，与图4相比系统响应时间T随λ的变化会有显著变化，如图5所示。而只改变其他某些参数如δ、τ、C1和C2时系统响应时间T却没有明显变化。换句话说，运算量μ和网络传输速度ω成为该系统的瓶颈。

由上述仿真结果，可以看出我们提出的模型不但能够很好地表达TOC的服务过程，而且可以揭示系统中各参数影响系统响应时间的规律，从而为提高系统效率提供解决方案。

4　小结

为分析和研究TOC的性能，确保QoS，本文基于M/M/1排队系统提出了一个TOC服务模型。在分析详细TOC任务管理系统各模块功能后，对不同的模块或模块组合基于M/M/1排队系统进行建模，而后将其级联，进而得到系统平均响应时间的计算公式。模型仿真显示运算量和广域网传输速度是影响系统响应时间的瓶颈。因此，要提高系统效率就必须分析和设计恰当的任务管理系统，以方便用户像使用电子计算机那样使用TOC，从而减少数据传输量。

［1］Jin Y，He H C，Lű YT.Ternary optical computer principle［J］.Science in China（Series F），2003，46（2）：145-150.

［2］Jin Y，He H C，Lű Y T.Ternary optical computer architecture［J］.Physica Scripta，2005，T118：98-101.

［3］Yan J Y，Jin Y，Zuo K Z.Decrease-radix design principle for carrying/borrowing free multi-valued and application in ternary optical computer［J］.Science in China Series F：Ⅰnformation Sciences，2008，51（10）：1415-1426.

［4］Jin Y，He H C，Ai L R.Lane of parallel through carry in ternary optical adder［J］.Science in China Ser.FⅠnformation Sciences，2005，48（1）：107-116.

［5］Wang H J，Song K.Simulative method for the optical processor reconfiguration on a dynamically reconfigurable optical platform［J］.Applied Optics，2012，51（2）：167-175.

［6］Song K，Liu Y P.Design and implementation of the one-step MSD adder of optical computer［J］.Applied Optics，2012，51（7）：917-926.

［7］ Peng J J，Shen R，Jin Y，Shen Y F，Luo S.Design and implementation of modified signed-digit adder［J］. ⅠEEE Transactions on Computers，2014，63（5）：1134-1143.

［8］Shen Y F，Pan L.Principle of a one-step MSD adder for a ternary optical computer［J］.Science ChinaⅠnformation Sciences，2014，57（1）：012107.

［9］Shen Z Y，Wu L L.Reconfigurable optical logic unit with a terahertz optical asymmetric demultiplexer and electro-optic switches［J］.Applied Optics，2008，47 （21）：3737-3742.

［10］Shen Z Y，Wu L L，Yan J R.The reconfigurable module of ternary optical computer［J］.Optik，2013，124：1415-1419.

［11］Wang X C，Zuo K Z.Topological properties of the opticaloperatorreconfigurationnetwork［J］.Applied Mathematics& Ⅰnformation Sciences，2015，9（4）：2057-2065.

［12］Song K，Jin Y.Overall plan and design of the task management system of ternary optical computer［J］.Journal of Shanghai University（English Edition），2011，15 （5）：467-472.

［13］Wang X C，Peng J J，Ouyang S.Control method for the optical components of a dynamically reconfigurable optical platform［J］，Applied Optics，2011，50（5）：662-670.

［14］Liu Y P，Song K.Communication mechanism of the monitor system of the ternary optical computer［J］，Ⅰnternational Journal of Digital Content Technology and itsApplications，2011，5（11）：283-289.

［15］Wang X C，Yao Y F，Wang C S，Sun W W，Wang K Z. Processor allocation of a ternary optical computer［J］. Advanced Science Letters，2013，19（6）：1714-1717.

［16］Wang X C，Yao Y F，Wang C S，Wang K Z.Dynamic data-bit allocation of a ternary optical computer［J］.Applied Mechanics and Materials，2012，109：181-186.

［17］Wang X C，Yao Y F，Wang C S，Sun W W，Wang K Z. Architecture of the monitor system in ternary optical computer［J］.Advanced Materials Research，2013，616-618：2158-2161.

［18］Wang X C，Peng J J，Li M，Shen Z Y，Ouyang S.Carryfree vector-matrix multiplication on a dynamically reconfigurableopticalplatform［J］.AppliedOptics，2010，49（12）：2352-2362.

［19］Khazaei H，Misic J，Misic V B.A Fine-Grained Performance Model of Cloud Computing Centers［J］.ⅠEEE Transactions on parallel and distributed systems，2013，24（11）：2138-2147.

［20］Vilaplana J，Solsona F，TeixidóⅠ，Mateo J，Abella F，Rius J.A queuing theory model for cloud computing［J］. The Journal of Supercomputing，2014，69（1）：492-507.

［21］Sandeep K S.Dynamic resource provisioning in cloud based on queuing model［J］.Ⅰnternational Journal of Cloud Computing and Services Science，2013，2（4）：314-320.

［22］Oumellal F，Hanini M，Haqiq A.MMPP/G/m/m+r queuing system model to analytically evaluate cloud computing center performances［J］.British Journal of Mathematics&Computer Science，2014，4（10）：1301-1317.

［23］Gross D，Shortie J F，Thompson J M，Harris C M.Fundamentals of queueing theory（Fourth Edition）［M］. New Jersey：John Wiley&Sons，Ⅰnc.

［24］Kleinrock L.Queueing systems：theory，vol 1［M］.New York：Wikey-Ⅰnterscience.

Servicing model of a ternary optical computer using M/M/1 queuing system

WANG Xian-chao，ZHANG Mian，WANG Chun-sheng，YAO Yun-fei

（School of Mathematics and Statistics，Fuyang Normal University，Fuyang Anhui 236037，China）

Quality of Service（QoS）is a crucial factor for the commercial success of a ternary optical computer（TOC）.This paper presents a task scheduling model for TOC based on first-come-first-service strategy，the M/M/1 queuing system and tandem queueing.And it uses the mean response time to analyze and evaluate the performance of TOC.The results demonstrate that the computation and network transmission speed is the bottleneck of system average response time.Therefore，the presented model is good for designing the task management systems of TOC.

M/M/1 queueing system；ternary optical computer；task scheduling；response time；tandem queue

TP302.7，TP38

A

1004-4329（2016）01-001-05

10.14096/j.cnki.cn34-1069/n/1004-4329（2016）01-001-05

2015-09-25

国家自然科学基金资助项目（61073049，61103054）；安徽省教育厅高校自然科学研究重点资助项目（KJ2015A191，KJ2015A182）；安徽省质量工程项目（2013zy167，2014zy138，2015jxtd121）；阜阳师范学院质量工程项目（2013ZYSD05，2014JXTD01）资助。

王先超（1973-），男，博士，副教授，研究方向：光计算。