有限覆盖定理的一般形式及其逆
2016-10-13胡绍宗
胡绍宗
(阜阳师范学院 数学与统计学院, 安徽 阜阳 236037)
有限覆盖定理的一般形式及其逆
胡绍宗
(阜阳师范学院 数学与统计学院, 安徽阜阳236037)
先将数学分析中的有限覆盖定理逐步拓广到一般度量空间,再予证明。
有限覆盖;有界闭集;紧集。
数学分析中所论述的Heine-Borel有限覆盖定理[1]为:
设F=[a,b]是一个闭区间,G是一个开区间族,它覆盖了F,则从G中可选出有限个开区间来覆盖F。
若将F换成直线上有界闭集,G换成开集族,则定理可推广为:
设F是直线上有界闭集,G是开集族,它覆盖了F,则从G中可选出有限个开集来覆盖F。
若将F换成n维闭区间,G换成开区间族,则定理可推广为:
设F={(x1,x2,…,xn)|ai≤xi≤bi,i=1,2,…,n}是一个n维闭区间,G是一个n维开区间族,它覆盖了F,则从G中可选出有限个开区间来覆盖F。
若将F换成n维有界闭集,G换成n维开集族,则定理可推广为:
设F⊂Rn是一个有界闭集,G⊂Rn是一个开集族,它覆盖了F,则从G中可选出有限个开集来覆盖F。
定义1设X为度量空间,F⊂X,如果F中的任何点列必有在X中收敛的子点列,则称F为X中的致密集。
注 度量空间中致密集是有界集[2] 88-89。
定义2度量空间中致密闭集称为紧集。
若将F换成一般度量空间X中的紧集,G换成X中开集族,则可得定理的一般形式为:
有限覆盖定理设X是一般度量空间,F⊂X是一个非空紧集,G⊂X是一个开集族,它覆盖了F,则从G中可选出有限个开集来覆盖F。
为了证明这个一般形式的有限覆盖定理,先证如下的紧集套定理。
紧集套定理设{Fk}是度量空间X中的非空紧集列,且满足:
(ⅰ)F1⊃F2⊃…⊃Fk⊃…,
(ⅱ)Fk的直径δ()Fk→0(k→∞),则存在唯一的点x∈Fk(k=1,2,…)。
证 不妨假定对一切k,Fk+1是Fk的真子集,
即

再证唯一性。设另有一点x′∈Fk(k=1,2,… ),则,由题设,于是d(x,x′)=0,从而x=x′。
有限覆盖定理的证明:用反证法。假定定理的结论不成立,即F不能被G中任意有限个开集所覆盖,因F为紧集,即致密闭集,从而为有界闭集,故可设F⊂闭集S}为X中某个定点,x∈X ,二等分线段R0R1,设分点为R2,则相应地将S分成两个闭集:{x|R0≤d(x0,x)≤R2}与,其中必有一个闭集与F的交非空且不能被G中有限个开集所覆盖,记这个闭集为S1,F1=F⋂S1是一个非空紧集,F1⊂S1。
再等分线段R0R2或R2R1,设分点为R3,则相应地将S1分成两个闭集:,或。
其中必有一个闭集与F1的交非空且不能被G中有限个开集所覆盖,记这个闭集为S2,F2=F1⋂S2是一个非空紧集,F2⊂S2,重复这个步骤并不断地进行下去,我们就可以得到一列紧集:
F⊃F1⊃F2⊃…⊃Fk⊃…,它们分别包含在S⊃S1⊃S2⊃…⊃Sk⊃…中
而Fk=Fk-1⋂Sk(k=1,2,…)不能被G中有限个开集所覆盖。
据Sk的作法可知,其直径,又因,故有。由紧集套定理,存在唯一点x-∈Fk(k=1,2,… ),当然更有x-∈F。
因为G覆盖F,所以存在开集G0∈G,使x-∈G0,当k充分大时,有Sk⊂G0,从而
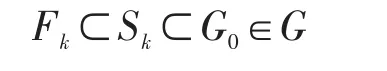
这说明Fk只须用G中一个开集G0就能覆盖,这与挑选Fk时的假设“不能用G中有限个开集来覆盖”相矛盾,从而证得G中必有有限个开集覆盖F。
要指出的是:由前面已知,紧集即致密闭集,也是有界闭集。试问上述定理的条件中紧集可不可以改为有界闭集?我们的回答是否定的,因为在一般的度量空间中有界集未必是致密集,从而有界闭集,不一定是致密闭集,即未必是紧集。例如
在闭区间[0,1]上作连续函数列

0,1中不是致密集。
这里还要指出的是:在n维欧几里得空间中,有界集和致密集是等价的[]2 96-98,从而有界闭集和致密闭集是等价的,即有界闭集和紧集是等价的。这正说明数学分析中所讲的有限覆盖定理是上述定理的特殊情形。
因此给出紧集的下面这种定义,即
定义3设X是度量空间,F⊂X,如果X中每个覆盖F的开集族中都有有限个开集覆盖F,则称F是紧集。
The general form of the finite covering theorem and its inverse
HU Shao-zong
(School of Mathematics and Satistics,Fuyang Normal University,Fuyang Anhui 236037,China)
First,the finite covering theorem in mathematical analysis was gradually extended to general metric space.And then it was proved.
finite covering;bounded closed set;compact set
O177
A
1004-4329(2016)01-016-02
10.14096/j.cnki.cn34-1069/n/1004-4329(2016)01-016-02
2015-09-08
国家特色专业(TS1496);安徽省质量工程项目(2013zy167,2014zy138,2015jxtd121)资助。
胡绍宗(1929-),男,副教授,研究方向:实分析。
[1] 华东师范大学数学系.数学分析(上册)[M].3版.北京:高等教育出版社,2001:165-166.
[2] 夏道行,吴卓人,严绍宗等.实变函数论与泛函分析(下册)[M].北京:人民教育出版社,1979:88-89,96-98.
