高精度光散射气溶胶质量浓度测量系统的信号处理研究*

张加宏，韦圆圆，顾　芳，冒晓莉2，，沈　雷，包志伟，汪　程，吴佳伟

（1.南京信息工程大学，江苏省大气环境与装备技术协同创新中心，南京210044；2.南京信息工程大学，江苏省气象探测与信息处理重点实验室，南京210044；3.南京信息工程大学，物理与光电工程学院，南京210044；4.南京信息工程大学，电子与信息工程学院，南京210044）

高精度光散射气溶胶质量浓度测量系统的信号处理研究*

张加宏1，2，4*，韦圆圆4，顾芳3，冒晓莉2，4，沈雷4，包志伟4，汪程4，吴佳伟4

（1.南京信息工程大学，江苏省大气环境与装备技术协同创新中心，南京210044；2.南京信息工程大学，江苏省气象探测与信息处理重点实验室，南京210044；3.南京信息工程大学，物理与光电工程学院，南京210044；4.南京信息工程大学，电子与信息工程学院，南京210044）

气溶胶质量浓度是评价大气环境变化的关键参数，光散射法是测量该参数的有效方法。但现有反演模型多采用散射光信号积分量反演质量浓度，导致颗粒物细化信息丢失，且未考虑颗粒形貌因素。针对上述问题，本文提出了一种采用散射光信号幅度分布反演气溶胶质量浓度的分形模型，充分利用了颗粒散射光的信号幅度信息与数目信息，有效提高了反演精度。实验结果表明:对于烟尘和空气样品，分形模型质量浓度反演值与实际测量值吻合，拟合直线斜率与1的绝对差为0.034 和0.016，相关系数高于0.999，实验平均相对误差均小于7.7%，而电压积分量反演的质量浓度平均相对误差则在18.7%以内。该研究为光散射法应用于在线监测气溶胶质量浓度提供了一种新的精确反演方法。

光散射；气溶胶质量浓度；信号幅度分布；分形；积分信号

EEACC:7320P；7220doi:10.3969/j.issn.1004-1699.2016.04.013

环境污染已成为全球性关注的重大问题，其显著表现之一是大气气溶胶颗粒物浓度不断升高。气溶胶颗粒物增多对人体健康和大气环境造成了诸多负面影响，具体表现在以下几方面［1-3］:①引起呼吸道疾病及心肺疾病，尤其是可入肺颗粒物PM2.5（空气动力学等效直径小于等于2.5 μm的颗粒）；②使得大气能见度降低；③吸收和散射太阳辐射，直接改变地─气系统的能量收支，影响气候变化；④导致酸沉降严重，使农业和林业等方面造成重大损失。因此，如何准确监测及控制大气气溶胶质量浓度是一项紧迫且具有重大经济意义的任务。迄今为止，人们已经发展了许多基于不同原理的气溶胶质量浓度测量方法［4-6］，为质量浓度监测提供了强有力的手段。其中，光散射法作为一类非常重要的非扰动测量方法，以测量速度快、精度高、重复性好、测量浓度范围宽及适用于在线非接触测量等优点得到了广泛应用。利用光散射原理测量质量浓度的方法主要有两类:一类是单粒子光散射法，也称为粒子计数法［7-9］；另一类是颗粒群光散射法（光度计法）［10-11］。

粒子计数法起初被广泛应用于测量洁净环境中颗粒数目浓度，近年来，该方法逐渐被用于测量颗粒物质量浓度。例如，Binning等人通过假设颗粒密度、折射率已知的条件下，利用等效直径的概念，由颗粒物的数目浓度反演出质量浓度［12］。阎逢旗等人通过对大气的长期监测，给出了粒子数与质量浓度之间的经验计算公式［13］。目前采用该方法的颗粒物质量浓度测量仪主要有德国Grimm公司的1100系列颗粒物分析仪［9］。值得注意的是，上述反演模型均是采用标定的方法确定每个计数通道的体积等效粒径，再由粒子计数器测量到的各通道颗粒数和颗粒物平均密度计算出被测颗粒物的质量浓度。换言之，上述算法是将与不规则颗粒具有相同散射光信号的标准球形颗粒的直径作为它的体积等效直径，但不规则颗粒的体积与它对应标准球颗粒的体积实际上并不相等，相等的是两者的散射光信号，因而这种不考虑颗粒形貌因素而反演的颗粒物质量浓度与实际值之间必然存在一定程度的偏差。颗粒群光散射法是通过测量颗粒群在某一空间角度处的散射光信号来反演颗粒物质量浓度。该方法的优点是适合在线测量高浓度颗粒物，且对小颗粒的散射光信号测量更敏感，有利于测量气溶胶中PM2.5质量浓度［14］。基于此方法的商品化仪器主要包括:美国TSI公司的AM510型智能防爆粉尘仪，8530型气溶胶监测仪以及美国SKC公司的EPAM5000可吸入颗粒物浓度测定仪等。颗粒群光散射法反演模型主要由Görner等人［10］建立，该模型采用颗粒群散射光信号的积分量来反演质量浓度，但光信号的总积分量会使得颗粒群细化的信息丢失，比如:散射光信号强度相等的颗粒个数信息及单个颗粒的散射光幅度信息，从而会影响到测量精度。在这种情况下，为提升该方法的精度，这类测量系统在硬件或软件补偿上的成本必然会有所增加。

根据上述说明可知，一方面，若不考虑颗粒形貌因素，将散射光信号幅度相等的球形颗粒质量作为被测非球形气溶胶颗粒的质量，质量浓度反演结果必然造成偏差；另一方面，若采用散射光信号的总积分量反演质量浓度会使得颗粒群细化的信息丢失，造成精度降低。因此，光散射气溶胶质量浓度反演时，考虑颗粒形貌因素和提取足够多的颗粒散射光信息对提高测量精度尤为关键。针对这些问题，在前期研究的基础上［7，15］，本文提出了光散射随机形貌分形维数的概念，进而建立了采用散射光信号幅度分布反演气溶胶质量浓度的分形模型。该分形模型不仅考虑了颗粒形貌因素，并且从细化颗粒群散射光信号信息的角度出发，采用粒子计数法光散射传感器输出的信号幅度分布反演气溶胶质量浓度。通过与电压积分量反演的质量浓度对比分析发现，分形模型具有更高的气溶胶质量浓度反演精度。

1　基于光散射法的气溶胶质量浓度测量系统

图1为本文实验所用粒子计数法测量气溶胶质量浓度系统的示意图，它由光学传感器和信号采集处理系统两部分组成。其中，光学传感器是测量系统的核心部件，它的结构和实物如图2所示。

图1　气溶胶质量浓度的测量系统示意图

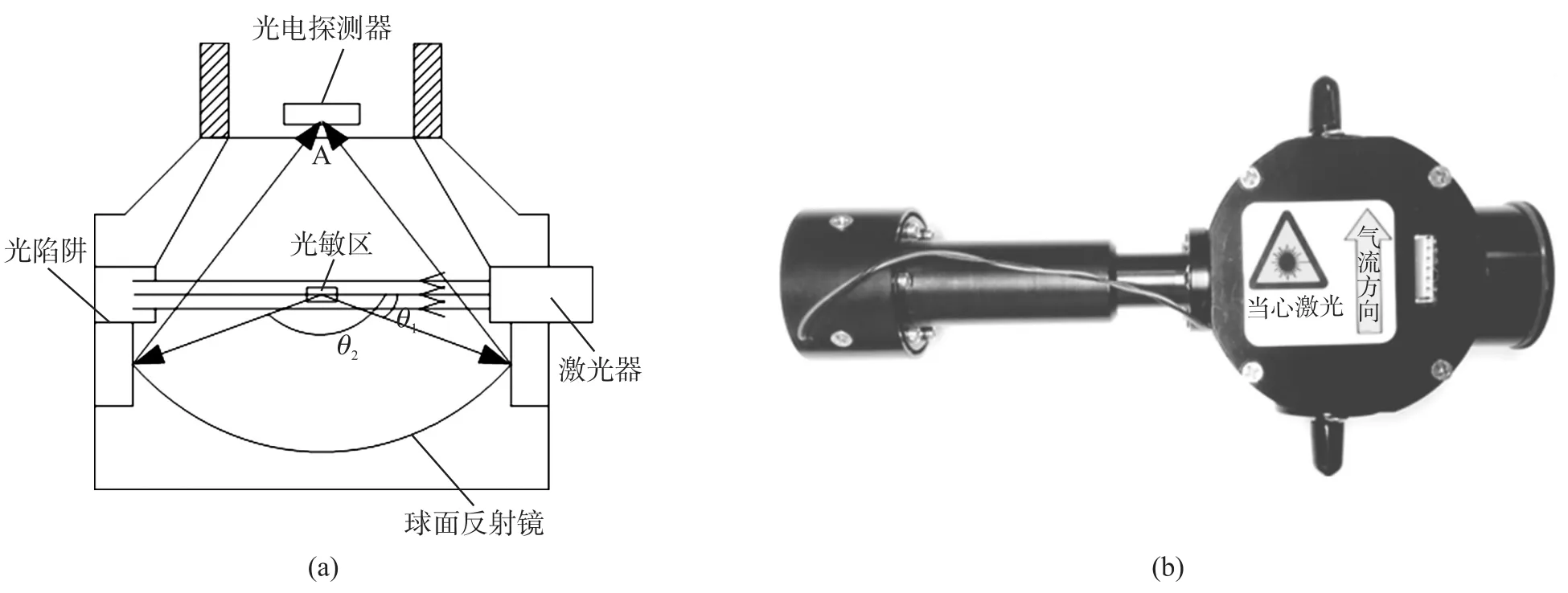
图2　光学传感器的（a）结构示意图和（b）实物图

当单个颗粒垂直于纸面通过光学传感器的光敏区时，颗粒会散射入射的激光（650 nm，15 mW），在90°采光角方向放置一块凹面镜收集某一立体角内（90°采光角对应的采光角范围为θ1到θ2，实际测量系统的散射光收集立体角约为π球面度）颗粒的散射光信号（即为颗粒的散射光通量），使之在另一点A处成像，再被光电探测器接收，并将接收的光信号转换成电脉冲信号，经前置放大、多通道计数，最终得到单个颗粒的电压脉冲信号，该脉冲信号的幅度与颗粒的尺寸及形貌密切相关。在一个测量周期内，测量系统得到的是一个个的电压脉冲信号，电压脉冲数即为颗粒数。颗粒物电压脉冲信号的幅度与脉冲数之间的关系称之为气溶胶颗粒物的电压脉冲信号幅度分布，如图3所示。由于颗粒的电压脉冲信号是由散射光信号转换得到，所以该分布与颗粒物的散射光信号幅度分布是等价的，本文将采用电压脉冲信号幅度分布反演气溶胶颗粒物的质量浓度。

图3　气溶胶颗粒物的电压脉冲信号幅度分布图

2　电压脉冲信号幅度分布反演质量浓度的分形模型

由前文可知，散射光的电压脉冲信号个数即为被测颗粒的个数信息，而脉冲信号的幅度却包含了颗粒的质量和形貌信息之和，那么如何从光散射传感器获得的这些信息反演气溶胶质量浓度将是本节讨论的主要问题。气溶胶颗粒物的质量浓度C是指单位体积气体中所含颗粒的总质量，数学表达式为:

其中，n指单位体积气体中被测颗粒的总个数，mi指某一个颗粒的质量。

根据式（1）可知，我们需要利用颗粒散射光脉冲的个数和幅度信息表示出单位体积气体中颗粒的总质量。据大量研究表明［16-19］，气溶胶颗粒的来源较多，使得它的形貌特征极其复杂，不同来源的颗粒具有不同的形貌特征，如碳质颗粒物为链状、燃煤颗粒物大多呈近似球形、扬尘中的矿物颗粒形貌较为复杂，有片状、柱状等，这样使用规则球形颗粒的质量计算公式πρD3/6（ρ和D表示颗粒的密度与直径）来表示不规则气溶胶颗粒的质量势必造成较大误差。因此，本文根据光散射传感器测量特点对气溶胶颗粒物进行了分类，将散射光信号幅度相等的被测颗粒分为一个颗粒群子集，于是被测颗粒物被分成了一系列的子集。每个子集中的颗粒虽然散射光信号幅度相等，但是它们的质量各不相等。值得注意的是，因测量过程中气溶胶颗粒流动的随机性及颗粒形貌的随机性，当气溶胶颗粒被大量统计测量时，即被测颗粒的数目足够多时，散射光信号幅度相等的颗粒群子集的平均质量（指散射光信号幅度相等的所有颗粒质量之和的平均值）应该基本不变，这是统计测量的必然结果。而如何表示颗粒群子集的平均质量将是问题的关键，下面我们将利用统计分形理论表示出颗粒群子集的平均质量。

文献［19-22］的研究表明:气溶胶颗粒物具有统计分形特征，即具有统计自相似性，该相似性并不是指颗粒形貌之间的严格相似，而是对颗粒群大量统计测量得到的自相似性。自相似性系统的定量性质可以用分形维数来衡量，分形维数可以不是整数［23］。因此，上述分析表明在统计测量的基础上，可以采用分形维数表征气溶胶颗粒的形貌特征，并用其表示出颗粒群子集的平均质量。于是，本文利用气溶胶颗粒的随机形貌分维数α和光学等效直径DF这两个物理量，将颗粒群子集的平均质量表示为:

实际上，对于规则的球形颗粒物而言，α等于3，而对于不规则的非球形颗粒物，α应该为1～3之间的任意数。此外，由光学传感器的测量原理可知，颗粒的光学等效直径DF与其脉冲信号电压v具有一一对应关系，这样就会有，其中 β表示颗粒物对应电压脉冲信号的分维数，它是气溶胶颗粒物形貌具有统计自相似性的体现。因此，颗粒群子集的平均质量又可表示为:

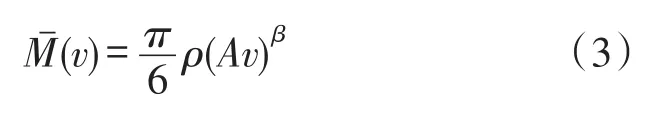
其中A为颗粒散射光信号与电压信号之间的转换系数。

因测量系统给出的电压脉冲信号幅度分布是离散的，所以根据气溶胶质量浓度的定义，得到了利用电压脉冲信号幅度分布和平均质量表示的质量浓度反演公式:

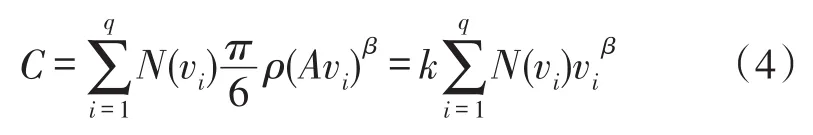
其中:q为颗粒群子集的数目或者电压脉冲信号的通道数，N（vi）为图1实验装置测量的气溶胶颗粒物的离散电压脉冲信号幅度分布，k为比例系数。式（4）的气溶胶质量浓度反演公式同时包含了各通道电压脉冲信号的个数信息N（vi）和幅度信息vi，使得被测气溶胶的散射光脉冲信号幅度分布得到了充分利用，且含有反映颗粒物形貌信息的参数β。不难理解，实现高精度质量浓度反演的关键是如何标定式（4）的比例系数k和电压脉冲信号的分维数 β。下面将对该问题进行详细讨论并给出实验测试结果，同时与采用颗粒群散射光信号积分量反演质量浓度的结果进行比较分析研究。

3　实验标定及测试结果对比分析研究

3.1高精度气溶胶质量浓度测量系统的实验标定

气溶胶质量浓度测量系统使用的分形模型中k和 β的标定方案如下3个步骤:首先，将某种气溶胶确定为标定样品，利用图1的实验装置与标定仪器（TSI公司，SIDEPAK AM510）同时对不同质量浓度的气溶胶进行统计测量。本文实验装置得到的是颗粒物电压脉冲信号幅度分布N（vi），该分布具有的脉冲信号通道数q=2 048，电压幅度范围为［0 V，5 V］，标定仪器得到的是颗粒物质量浓度值CTSI；其次，由于在标定实验中只能取某种类气溶胶中的小样本对测量系统进行标定，而小样本颗粒物的形貌特征是有差异的，所以不同小样本的脉冲信号分维数β值也是存在差异。如图4所示，我们通过多次取样进行标定，提取小样本的共同形貌特征来表示某种类气溶胶颗粒物的形貌特征，这样，根据如下方程组即可得到k和β:

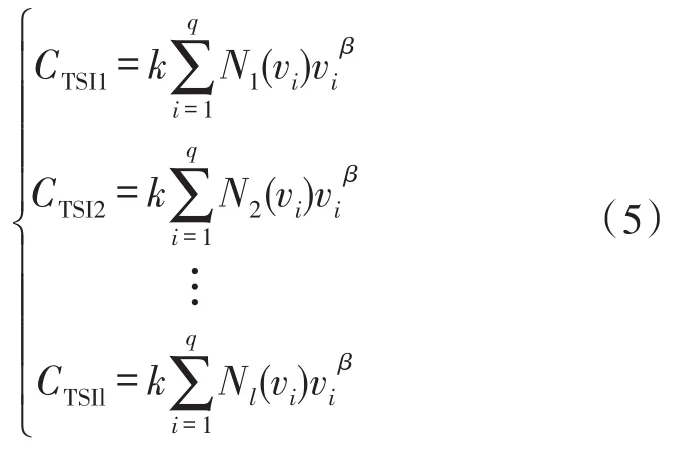
其中，l表示被测气溶胶小样本的数目。

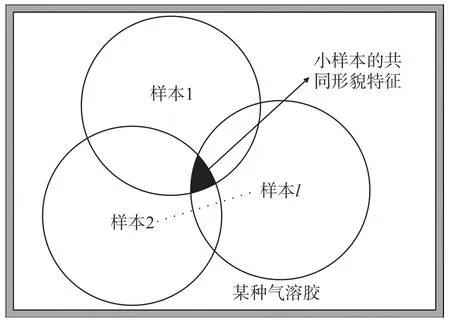
图4　标定方法的原理示意图

本文标定实验中，在不同的时间对同种类的烟尘进行了五次采样，获得五个小样本，并采用图1的实验装置进行了测量，分别记录了标定仪器测量的烟尘质量浓度CTSI及本文实验系统测量的电压脉冲信号幅度分布N（vi）。实验过程中，对测量环境的温度和相对湿度进行了控制与实时监测，尽量使得环境相对湿度小于60%，从而避免环境因素对标定实验产生不良影响［24］。最后，利用式（5）对颗粒物质量浓度分形模型中的k和β进行标定，标定结果如表1所示。

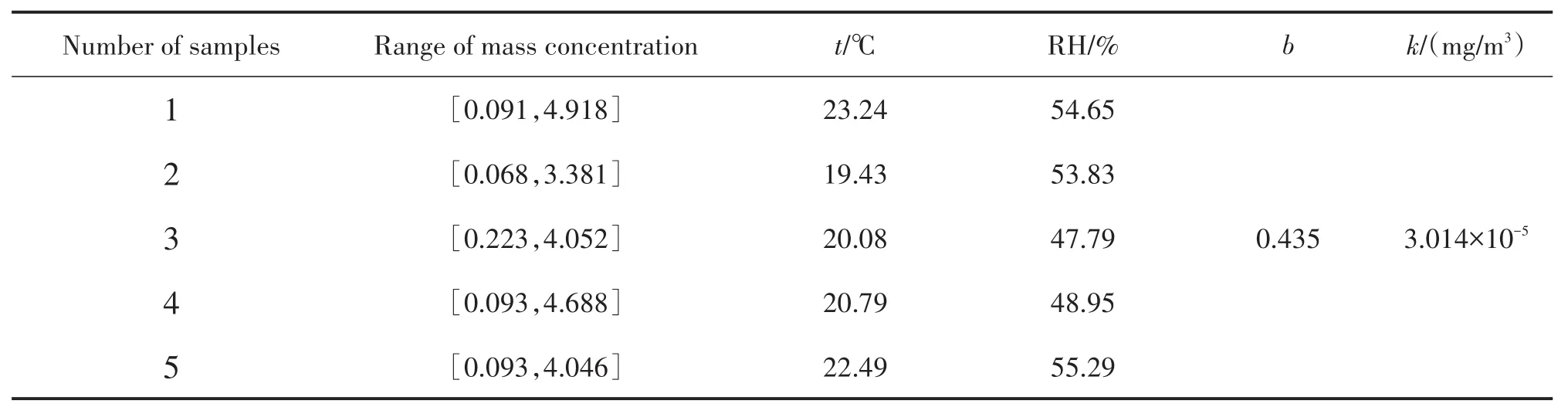
表1　气溶胶质量浓度测量系统的标定结果

3.2实验测试结果对比研究

为了验证上述标定方法的可靠性，在0.001 mg/m3～5 mg/m3质量浓度范围内，利用标定之后的气溶胶质量浓度测量系统分别对烟尘和空气进行了两次测量，记录了颗粒物的电压脉冲信号幅度分布N（vi）及标定仪器质量浓度值CTSI。将表1中的 β和k代入到质量浓度的反演公式（4），即可求出本文实验系统测量的烟尘和空气质量浓度C，并将C与CTSI进行了比较。图5为烟尘样品的两次实验结果，其中，图5（a）和（c）是分形模型的反演值C与CTSI的关系图，从图中数据点的分布可以看出，随着质量浓度的变化，两台仪器测量值存在明显的线性关系，故对这些数据点进行了线性回归计算。拟合直线方程、相关系数R2、数据组数Num及数据点的均方差SD如图5（a）和5（c）所示，两次实验拟合直线的斜率分别为 1.034和 0.984，相关系数分别为0.999 8和0.999 2。由此可见，两次实验拟合直线的斜率均与1比较接近，相关系数都在0.999以上，表明基于电压脉冲信号幅度分布的分形模型反演的烟尘质量浓度值C与标定仪器的测量值CTSI基本一致，且两者具有很高的相关性。图5（b）和（d）给出了两次实验C与CTSI之间的相对误差，所有测量点相对误差的平均值Ecavg分别为 4.4%和 6.2%，同样说明了C与 CTSI吻合较好。

图5　分形模型的反演值C与标准仪器测量值CTSI之间的关系，烟尘

图6为空气样品的两次实验结果。由于空气质量浓度的变化范围较小，集中在0.1～0.3 mg/m3之间，C与CTSI不易表现出线性关系，因此，图6（a）和6（c）分别给出了质量浓度值随测量周期数的变化关系，从图中不难发现，C与CTSI具有相同的变化趋势，且两者之间的差异较小；图6（b）和（d）给出了它们的相对误差分布图，所有测量点相对误差的平均值Ecavg分别为7.7%和7.2%，表明空气样品的C与CTSI吻合较好。

图6　分形模型的反演值C与标准仪器测量值CTSI之间的关系，空气

上述两组实验结果均证实了本文提出的采用颗粒群散射光信号幅度分布反演气溶胶质量浓度的方法是正确的，能够有效应用于实际测量。为了进一步说明该方法的精确度，将图5和图6的反演结果与利用颗粒群散射光信号积分量反演质量浓度的测量结果进行比较研究。采用积分量来反演质量浓度CT的公式如下:

其中，Tv为一个测量周期内的散射光电压脉冲信号积分量，k′为标定系数。

类似地，首先需要标定出系数k′，对表1中5次标定实验的颗粒物电压脉冲信号幅度求和，得到每个测量周期的电压脉冲信号积分量Tv，再分别对五次标定实验的两组数据CTSI和Tv按照公式（7）进行线性拟合，拟合直线的斜率即为标定系数k′，这样得到了五次实验的标定系数k1′、k2′、k3′、k4′、k5′；最后取平均值k′=（k1′+k2′+k3′+k4′+k5′）/5用于反演气溶胶质量浓度，标定结果如表2所示。

其次，将标定系数k′用于实际测量，并与分形模型的结果进行比较。

对图5和图6所示的烟尘和空气的电压脉冲信号幅度的电压值求和，得到每个测量周期的散射光的电压信号积分量Tv，将Tv和表2中的标定系数k′代入式（6）即可得到各个周期的质量浓度反演值CT。

表2　气溶胶散射光信号积分量反演质量浓度的标定结果

图7给出了烟尘样品的两次实验结果，其中，图7（a）和（c）是积分量反演值CT与CTSI的关系图，两次实验拟合直线的斜率分别为1.089和1.059，相关系数分别为0.999 7和0.999 3。由此可见，CT与CTSI之间也具有较好的相关性和线性关系，但是拟合直线的斜率与1的差值分别为0.089和0.059，要大于图5（a）和5（c）中拟合直线的斜率与1的差值0.034和0.016，这说明采用电压脉冲信号幅度分布反演的质量浓度与实际测量值更接近。此外，图7（b）和7（d）还计算出了CT与CTSI之间的相对误差，所有测量点相对误差的平均值 Ecavg分别为 7.4%和10.1%，明显大于图5（b）和（d）计算的相对误差平均值4.4%和6.2%，同样说明了C比CT更精确。图8给出了空气样品的两次实验结果。图8（a）和8（c）分别给出了质量浓度值随测量周期数的变化关系，从图中可以看出，CT与CTSI具有相同的变化趋势，但是两者之间的具有显著的差异；图8（b）和8（d）为两者的相对误差分布图，所有测量点相对误差的平均值Ecavg分别为18.7%和 16.2%，明显高于图6（b）和6（d）计算的相对误差平均值7.7%和7.2%。

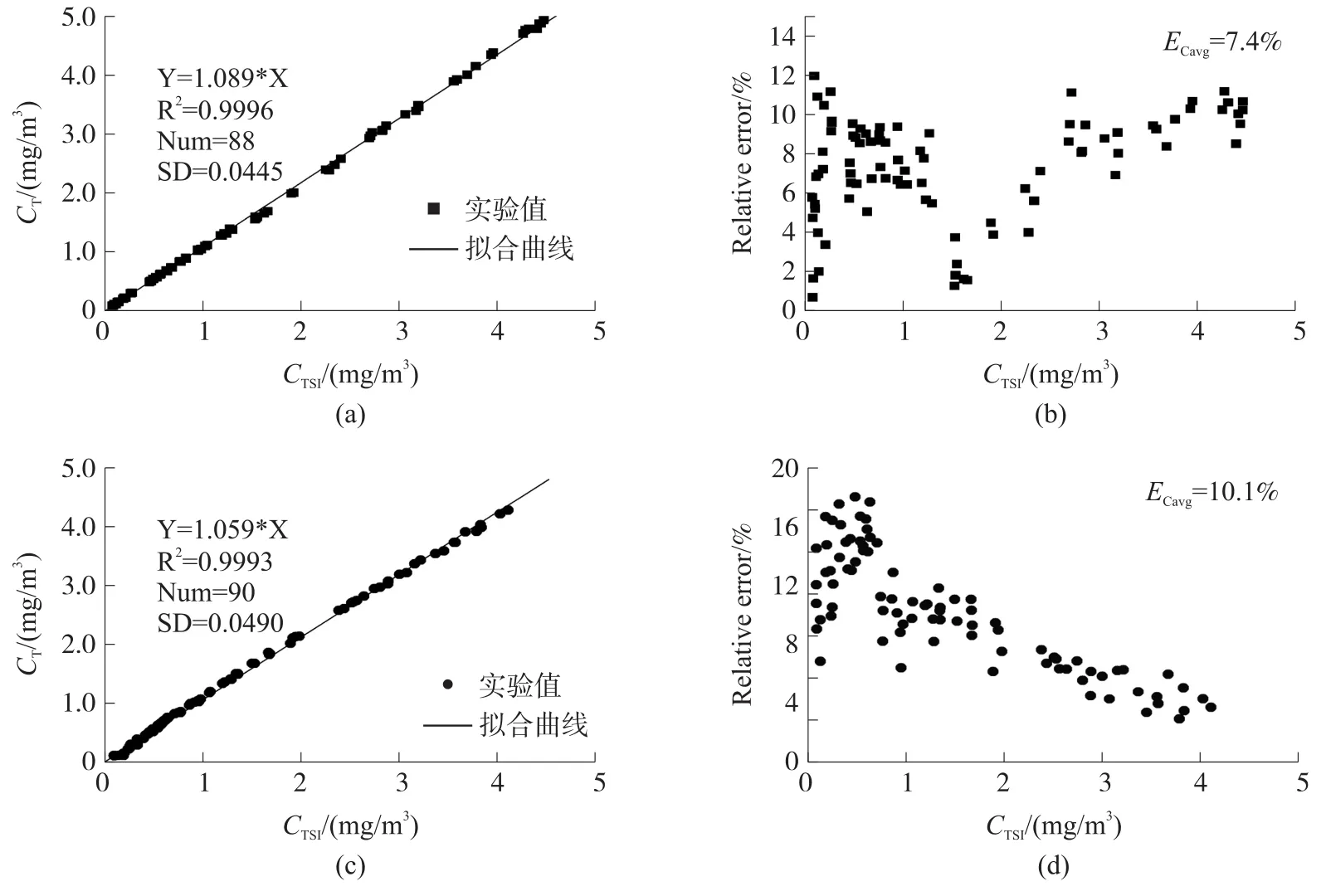
图7　积分量的反演值CT与标准仪器测量值CTSI之间的关系，烟尘

图8　积分量的反演值C与标准仪器测量值CTSI之间的关系，空气

综上所述，从考虑颗粒形貌和细化颗粒群散射光信息的角度出发，采用颗粒群散射光电压脉冲信号幅度分布反演气溶胶质量浓度的分形模型具有更高的精度。此外，由Mie散射理论知，颗粒的散射光信号与被测颗粒的折射率密切相关，所以颗粒的折射率会影响气溶胶质量浓度测量系统的散射光信号，进而影响输出的电压脉冲信号幅度大小；颗粒形貌对散射光信号也具有较大影响，不同来源的颗粒具有不同的形貌特征；而且环境湿度对颗粒物质量浓度的测量同样有较大影响，研究表明［25］:有亲水特性的气溶胶粒子（如硫酸盐、硝酸盐和一些有机气溶胶）吸湿增长可提高气溶胶的散射能力，从而影响颗粒的散射光信号，且气溶胶亲水能力越强，其对散射系数的影响越大。因此，如果被测颗粒与标定颗粒的折射率、形貌特征及标定的环境湿度等因素存在较大差异时，还需对测量系统的参数进行重新标定或者数据融合修正［26］。

4　结论

本文从细化气溶胶颗粒物散射光信号信息和考虑其形貌统计自相似性的角度出发，提出了随机形貌分形维数和颗粒物子集平均质量的概念，建立了利用气溶胶颗粒物散射光信号幅度分布反演质量浓度的分形模型。实验结果表明，本文颗粒物质量浓度分形模型得到的测量值与实际测量值吻合较好，拟合直线斜率与1的绝对差分别为0.034和0.016，相关系数达到0.999以上，且四组实验的平均相对误差都在7.7%以内；而采用电压积分量反演的质量浓度值与实际测量值的平均相对误差在18.7%以内。因此，基于散射光脉冲信号幅度分布反演的气溶胶质量浓度的测量系统具有更高的精度。本文的研究成果正好符合国家当前对大气环境监测的实际需求，也进一步使得光散射法测量气溶胶质量浓度的理论更加完善。

［1］ 韦莲芳，杨复沫，谭吉华，等.大气气溶胶消光性质的研究进展［J］.环境化学，2014，33（5）:705-715.

［2］ Cox Jr L A.Caveats for Causal Interpretations of Linear Regression Coefficients for Fine Particulate（PM2.5）Air Pollution Health Effects［J］.Risk Analysis，2013，33（12）:2111-2125.

［3］ Adachi K，Chung S H，Buseck P R，et al.Shapes of Soot Aerosol Particles and Implications for Their Effects on Climate［J］.Journal of Geophysical Research，2010，115（D15）:D15206.

［4］ 邹丽新，季晶晶，朱桂荣，等.空气悬浮颗粒物粒径分布及质量浓度一体化测量系统的研制［J］.传感技术学报，2007，20（8）: 1788-1792.

［5］ 梁艳，张增福，陈文亮，等.基于β射线法的新型PM2.5自动检测系统研究［J］.传感技术学报，2014，27（10）:1418-1422.

［6］ Winkel A，Llorens Rubio J，Huis in't Veld J W H，et al.Equivalence Testing of Filter-Based，Beta-Attenuation，TEOM，and Light-Scattering Devices for Measurement of PM10 Concentration in Animal Houses［J］.Journal of Aerosol Science，2015，80:11-26.

［7］ 顾芳，杨娟，卞保民，等.基于平均质量的悬浮颗粒物质量密度算法［J］.光学学报，2007，27（9）:1706-1710.

［8］ Görner P，Simon X，Bémer D，et al.Workplace Aerosol Mass Concentration Measurement Using Optical Particle Counters［J］.Journal of Environmental Monitoring，2012，14（2）:420-428.

［9］ Thomas P，Darrin O，Vijay G，et al.Comparison of the Grimm 1.108 and 1.109 Portable Aerosol Spectrometer to the TSI 3321 Aerodynamic Particle Sizer for Dry Particles［J］.Annals of Occupational Hygiene，2006，50:843-850.

［10］Görner P，Bemer D，Fabriès F，et al.Photometer Measurement of Polydisperse Aerosols［J］.Journal of Aerosol Science，1995，26: 1281-1302.

［11］Jiang R T，Viviana A B，Cheng K C，et al.Determination of Response of Real-Time SidePak AM510 Monitor to Secondhand Smoke，Other Common Indoor Aerosols，and Outdoor Aerosol［J］. Journal of Environmental Monitoring，2011，13（6）:1695-1720.

［12］Binnig J，Meyer J，Kasper G，et al.Calibration of an Optical Particle Counter to Provide PM2.5 Mass for Well-defined Particle Materials［J］.Aerosol Science，2007，38:325-332.

［13］阎逢旗，胡欢陵，虞统.用光学粒子计数器测颗粒物质量浓度和能见度［J］.量子电子学报，2004，21（1）:98-102.

［14］Wang X L，Chancellor G，Evenstad J，et al.A Novel Optical Instrument for Estimating Size Segregated Aerosol Mass Concentration in Real Time［J］.Aerosol Science and Technology，2009，43 （9）:939-950.

［15］顾芳，杨娟，王春勇，等.基于等效球形颗粒数的颗粒物质量浓度算法［J］.光电子·激光，2008，19（1）:87-91.

［16］李泽熙，邵龙义，樊景森，等.北京市不同天气条件下单颗粒形貌及元素组成特征［J］.中国环境科学，2013，33（9）:1546-1552.

［17］樊景森，邵龙义，李泽熙，等.云南宣威地区燃煤排放PM10的微观形貌和粒度特征［J］.环境科学研究，2013，26（10）:1035-1042.

［18］Colbeck I，Atkinson B，Johar Y，et al.The Morphology and Optical Properties of Soot Produced by Different Fuels［J］.Journal of Aerosol Science，1997，28（5）:715-723.

［19］Gwaze P，Schmid O，Annegarn H J，et al.Comparison of Three Methods of Fractal Analysis Applied to Soot Aggregates From Wood Combustion［J］.Journal of Aerosol Science，2006，37（7）: 820-838.

［20］Olfert J S，Symonds J P R，Collings N，et al.The Effective Density and Fractal Dimension of Particles Emitted From a Light-duty Diesel Vehicle with a Diesel Oxidation Catalyst［J］.Journal of Aerosol Science，2007，38（1）:69-82.

［21］Virtanen A，Ristimäki J，Keskinen J，et al.Method for Measuring Effective Density and Fractal Dimension of Aerosol Agglomerates ［J］.Aerosol Science and Technology，2004，38（5）:437-446.

［22］张青，邓小玖，张启兴，等.火灾烟颗粒分形模型和球形模型光散射的比较研究［J］.物理学报，2010，59（10）:7442-7446.

［23］张启忠，席旭刚，罗志增.多重分形分析在肌电信号模式识别中的应用［J］.传感技术学报，2013，26（2）:282-288.

［24］Gurumurthy R，John L A，Gregory C P，et al.Characterizing Indoor and Outdoor 15 Minute Average PM2.5 Concentrations in Urban Neighborhoods［J］.Aerosol Science and Technology，2003，37 （1）:33-45.

［25］Tang I N，Tridico A C，Fung K H，et al.Thermodynamic and Opti-cal Properties of Sea Salt Aerosols［J］.Journal of Geophysical Research，1997，102:23269-23275.

［26］龚雪飞，刘萍，简家文.基于PSO算法集成神经网络的多元有害气体检测系统［J］.传感技术学报，2015，28（6）:938-942.

张加宏（1979-），男，博士，南京信息工程大学电子与信息工程学院副教授，硕士研究生导师，主要从事微纳电子机械系统与气象传感器探测技术等相关研究工作，zjhnuist@163.com；

韦圆圆（1989-），女，南京信息工程大学电子与信息工程学院硕士研究生，主要从事大气环境光电检测技术方面的研究，wyyahjs@163.com；

顾芳（1981-），女，博士，南京信息工程大学物理与光电工程学院副教授，硕士研究生导师，本文通讯作者，主要从事大气颗粒物的激光检测技术和光电功能材料性能表征研究，gfnuist@163.com。

Research on Signal Processing of High-Precision Light-Scattering Measurement Systems for Aerosol Mass Concentrations*

ZHANG Jiahong1，2，4*，WEI Yuanyuan4，GU Fang3，MAO Xiaoli2，4，SHEN Lei4，BAO Zhiwei4，WANG Cheng4，WU Jiawei4
（1.Jiangsu Collaborative Innovation Center on Atmospheric Environment and Equipment Technology，Nanjing University of Information Science and Technology，Nanjing 210044，China；2.Jiangsu Key Laboratory of Meteorological Observation and Signal Processing，Nanjing University of Information Science and Technology，Nanjing 210044，China；3.School of Physics and Optoelectronic Engineering，Nanjing University of Information Science and Technology，Nanjing 210044，China；4.School of Electronic and Information Engineering，Nanjing University of Information Science and Technology，Nanjing 210044，China）

Aerosol mass concentration is a critical parameter for evaluating the changes in the atmospheric environment，and the light scattering method is an effective method to measure this parameter on-line.However，the integrated optical signal is commonly utilized to inverse aerosol mass concentration in the currently existing inversion models，which makes the optical information of aerosols loss.Meanwhile，the factor of particle shape has not been considered.To solve these problems，this paper proposes a fractal model for aerosol mass concentration by using the pulse signal amplitude distribution of scattering light from aerosols.This model takes full advantage of the information of the signal amplitude and the corresponding number of signals，which can effectively improve the inversion accuracy.The experimental results indicate that the mass concentrations based on the fractal model are in agreement with the actual measured values for the dust and air samples.The absolute errors between the slope of the fitted line and 1 are 0.034 and 0.016，the correlation coefficients are above 0.999，and the average relative errors are less than 7.7%.But the average relative errors of mass concentrations inversed through the integrated optical signal are less than 18.7%.The study provides a new accurate method for the online monitoring of the aerosol mass concentration based on the light scattering.

light scattering；aerosol mass concentration；signal amplitude distribution；fractal；integrated signal

TN247；TN911.7

A

1004-1699（2016）04-0536-09

项目来源:国家自然科学基金项目（61307113，61306138）；江苏省自然科学基金项目（BK2012460）；江苏省高等学校大学生实践创新训练计划项目（201510300034）；江苏省信息与通信工程优势学科建设项目

2015-08-06修改日期:2016-01-15