公司盈利、投资与资产定价：基于中国股市的实证

高春亭，周孝华



公司盈利、投资与资产定价：基于中国股市的实证

高春亭，周孝华

（重庆大学经济与工商管理学院，重庆400030）

选取1997年7月至2015年6月中国股市月度收益数据为样本，以营业利润与账面价值的比值作为盈利因素的代理变量，以总资产增长率作为投资因素的代理变量。先后运用Fama-Macbeth回归法和投资组合因子模拟法分析了规模、B/M、盈利和投资等因素与资产定价的关系，并对Fama和French近期提出的五因子资产定价模型进行了实证研究。研究发现，规模、B/M、盈利和投资四因素在解释个股横截面收益差异上的显著性依次降低，而且B/M因素在规模大组的显著性要大于规模小组，但盈利和投资因素则表现相反；中国股市的平均收益同样存在与规模、B/M、盈利和投资相关的效应特征，其中B/M效应特征表现出了翘尾现象，盈利效应的主要特征表现为盈利能力越强的公司的股票收益越低，但规模较大的公司则表现为盈利能力越强的公司的股票收益越高，投资效应特征表现为投资越保守的公司的股票收益越高。使用五因子资产定价模型能较好地拟合这些特征，而且在表现上也优于三因子资产定价模型。

资产定价；五因子模型；盈利；投资; Fama-Macbeth回归

0 引言

自20世纪60年代Sharpe[1]等在投资组合理论的基础上提出CAPM模型以来，资产定价理论在数理方面和实证方面的研究得到了迅速发展。在CAPM模型的实证检验方面，Black等[2]首次使用美国股市数据进行了研究。Fama和Macbeth[3]使用滚动“横截面”回归的方法进一步对CAPM模型进行了实证检验。但是，CAPM模型是只从市场风险溢价方面对股市的资产定价进行解释的单一因子模型，而没有考虑上市公司的特质性因素对资产定价的影响。后来的文献如Banz[4]等和Stattman[5]等发现美国股市中存在规模(Size)效应和账面市值比(B/M)效应。Fama和French[6]结合CAPM模型的思想和规模效应、账面市值比效应，提出了基于市场风险因素、规模效应因素和账面市值比因素的三因子资产定价模型，对学术界和实务界产生了深远影响。后期的学者从不同角度对三因子模型进行了改进和发展，如Carhart[7]将动能因素加入到三因子模型中提出了四因子模型。近期的研究如文献Novy-Marx[8]、Aharoni等[9]等发现，上市公司的盈利因素、投资因素与它们的市场表现之间存在一定的规律。Hou等[10]使用美国股市的周收益率数据构建了包含盈利因素和投资因素的q因子模型，并用该模型研究了美国股市的异象。同期，Fama和French[11]也将这两个因素加入到他们以前提出的三因子模型中提出了五因子资产定价模型。他们的实证研究表明，五因子模型在解释美国股市的横截面平均收益特征上比三因子模型表现更好。Eoghan和Michael[12]比较了Fama-French三因子模型和五因子模型在英国股市的表现，发现五因子模型在表现上要优于三因子模型。

与美国股市不同，我国股市才成立了二十多年，市场还不成熟。Fama-French三因子资产定价模型在我国股市里表现如何？对这一问题，国内的学者在不同时期先后对这一模型的适用性进行了检验。范龙振和王海涛[13]先后使用Fama-Macbeth回归法和模拟因子法对沪市1995年7月到2000年6月的资产定价因素进行了研究，发现沪市表现出显著的规模效应、账面市值比效应、市盈率效应和价格效应。但这些效应不能完全由Fama-French三因子模型进行解释，而加上市盈率因子的四因子模型则可以很好地解释。杨炘和陈展辉[14]使用1997年5月至2001年12月我国沪深A股的月度数据对三因子模型进行实证研究，研究表明三因子模型可以完全解释我国股市的横截面收益差异。邓长荣和马永开[15]使用1996年1月至2003年12月的月度收益数据研究了三因子模型在深市的表现并检验了“新年效应”异象，发现三因子模型在深市是成立的，而且低账面市值比上市公司(除小规模公司)的收益表现出了“一月效应”，中等规模且中等账面市值比的组合表现出了“二月效应”。刘维奇等[16]以2005年4月为分界点，研究了我国股市股权分置改革前后三因子模型的拟合情况，发现三因子模型在股权分置改革前后都是有效的，而且三个因素在股权分置改革后对横截面收益的解释度都有所提升。田利辉等[17]对比研究了1994年7月至2013年6月三因子模型在中美两国股市表现上的差异。发现虽然三因子模型能够很好地解释中美两国投资组合的平均收益，但中国股市市场风险因素作用更显著，而账面市值比效应却并不显著。李倩和梅婷[18]以沪市A股上市公司为样本，研究了三因子模型在股票价格上涨和衰退时期的适用性。发现在股市衰退期三因子模型表现最好，但账面市值比因素不显著。总的来看，国内大部分的研究都表明在我国股市里三因子模型是适用的而且规模效应显著，但在账面市值比效应的显著性上尚存在争议。也有的学者对三因子模型进行了拓展，探讨了其它因素在资产定价中的解释能力，如潘莉和徐建国[19]、田利辉和王冠英[20]等。但是从盈利和投资的视角进行的研究还相当缺乏，这方面仅有王茵田和朱英姿[21]使用净利润与市值的比值作为盈利因子、使用投资支出与固定资产净值的比率作为投资因子进行了研究。但尚未有学者像Fama和French[11]、Hou等[10]那样构建盈利因子和投资因子对我国股市的资产定价进行研究。那么，盈利因素和投资因素在中国股市里对资产定价会有怎样的影响？显著性又如何？探讨这些问题对深入认识我国股市资产定价的决定因素具有重要意义。

本文的研究特点有两个方面：一是同时使用Fama - Macbeth回归法进行横截面回归和模拟因子法进行时间序列回归对中国股市的资产定价影响因素进行研究。二是在使用Fama-Macbeth回归分析时分规模小组和规模大组进行了研究，比较了规模、账面市值比、盈利和投资四个因素在规模大组和规模小组的不同表现。

1 五因子资产定价模型的主要理论

Fama和French[11]通过分析Miller和Modigliani[22]的估值模型指出股票的期望收益与上市公司的账面市值比(B/M)、盈利和投资等因素相关。Miller和Modigliani[22]认为时期上市公司的市场价值可以由下式给出：

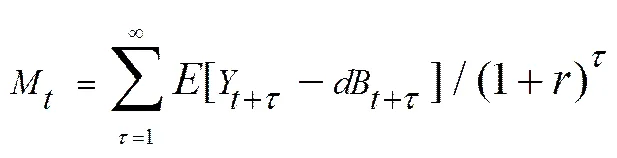
(2)

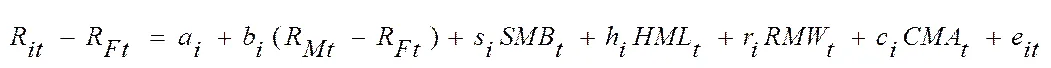
为了进行实证比较，本文同样给出Fama和French[6]以市场因素、规模因素和账面市值比因素为基础提出的三因子资产定价模型的具体形式，如下：

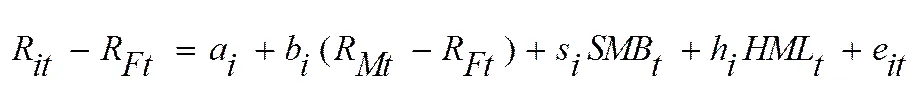
在上式中，各变量和系数的意义与(3)式相同。

2 样本选取和研究设计

2.1 数据选取和处理

本文财务数据来自Wind数据库，股票月度收益数据来自国泰安数据库。考虑到我国股市1996年12月16日实施了涨跌停板制度，本文选取1997年7月至2015年6月的沪深A股月度收益数据作为实证研究样本；以三个月定期利率转换的月利率作为无风险利率；选取样本股流通市值加权的股票月度收益率作为市场组合收益率。筛选样本标准是以上一年末（t-1年）所有A股上市公司为初始样本，依次剔除金融行业的公司、当年（t年7月至t+1年6月）实施ST和*ST 的公司、账面价值为负的公司、其他数据缺失或数据错误的公司。

2.2 研究设计

为了探讨五因子资产定价模型在我国股市的表现，本文从定义研究指标、使用Fama-Macbeth回归分析各因素的显著性、进行股票分组和因素指标的模拟计算等步骤依次展开。

研究指标的定义：无风险收益率使用三个月定期利率转换的月利率计算；市场收益率由样本股流通市值加权的股票月度收益率得到；公司规模(Size)用第t-1年末的股价与流通股数量的乘积来表示；账面市值比(B/M)使用第t-1年末股东所有者权益合计的值与总市值的比值来计算；在Fama和French[11]的研究中，他们使用(年收入-商品销售成本-利息费用-销售及一般管理费用)/账面价值测度上市公司的运营盈利能力，本文使用第t-1年末利润表中的营业利润与账面价值的比值作为盈利(OP)的代理变量；同时根据Fama和French[11]的思路，采用资产负债表中第t-1年末总资产(TAt-1)相对第t-2年末总资产(TAt-2)的变化率(也即(TAt-1-TAt-2)/TAt-2)作为上市公司投资水平(Inv)的代理变量。

研究方法：本文首先使用Fama-Macbeth两步法进行横截面回归分析，研究规模因素、账面市值比因素、盈利因素和投资因素对个股横截面收益差异的解释能力；然后再构建投资组合模拟构造各种因素因子进行时间序列回归分析，研究五因子资产定价模型的实证表现。

（1）使用Fama-Macbeth两步法进行横截面回归分析

Fama-Macbeth两步法由Fama和Macbeth[3]在检验CAPM模型时首次提出，其后广泛应用于资产定价实证研究中，该方法在检验影响横截面差异因素的显著性上具有优势。在本文里，我们使用该方法检验规模因素、账面市值比因素、盈利因素和投资因素在解释个股横截面收益差异上的显著性。在这部分研究中，使用第t-1年末流通市值的对数作为规模因子，记为；使用第t-1年末账面市值比(B/M)的对数作为账面市值比因子，记为；盈利因子和投资因子分别按照研究指标定义中的方法直接计算得到，并分别记为和。当同时使用四个因子对时的个股横截面收益进行解释时，模型可以表示为：

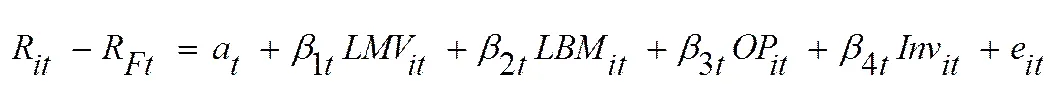
依据Fama-Macbeth两步法的思想，第一步先使用上述模型对时个股的横截面超额收益进行回归，得到各因子的系数的估计值。用同样方法，可以对期的横截面个股超额收益回归，从而各因子都可以得到个系数。第二步使用下述服从自由度为的学生分布的统计量进行检验，判断各因子系数是否显著异于零。

(6)

（2）构建投资组合模拟因子进行时间序列回归分析

构建投资组合模拟因子法是Fama和French[6]、Fama和French[11]研究中使用的主要方法，其主要思想包括股票分组、因子指标的计算和回归分析。下文只探讨前两步，回归分析将在实证部分给出。

股票分组：使用我国股市1997年7月至2015年6月的上市公司月度收益数据减去当月无风险利率得到相应的月度超额收益，再逐年按流通市值对每年的样本进行排序分成规模由小到大的五组，然后再分别按B/M、OP和Inv进一步细分成五组构建5×5投资组合，然后计算得到各投资组合流通市值加权的月度平均超额收益。由此得到的5×5投资组合月度平均超额收益有两方面用途，一是对得到的所有月份平均超额收益进一步平均，分析我国股市里各因素在横截面平均收益上表现出来的特征；二是作为(3)中左边的部分用于五因子资产模型的时间序列回归分析中。

因子指标的计算方法：为了方便分析，本文首先按照Fama和French[11]中构建2×3组合的方法定义(3)式中右边的各因子。具体来说，先按规模大小排序分成两组并分别标记为规模小组(S)和规模大组(B)。然后以得到30%，40%和30%比例股票的方法，再将规模小组和规模大组分别按账面市值比差异、盈利差异和投资差异分成三组，从而依次得到账面市值比高(H)、中(N)和低(L)的三组，盈利能力强(R)、中(N)和弱(W)的三组，投资保守(C)、中性(N)和激进(A)的三组。然后再按以下方式计算各因子：

上式中，SH表示规模小(S)且账面市值比高(H)的投资组合的流通市值加权的月度平均收益，而表示账面市值比高(H)的投资组合的月度平均收益减去账面市值比低(L)的投资组合的月度平均收益，其它符号意义类似。

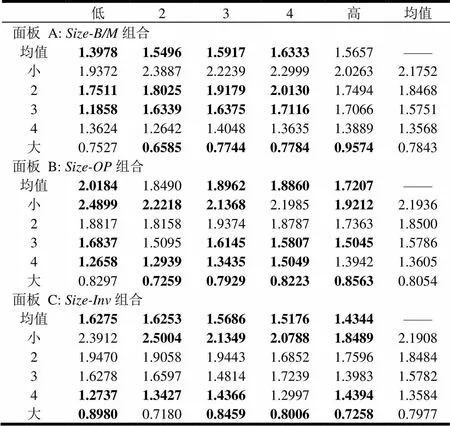
表1 5×5投资组合月度平均收益（%）（1997.7-2015.6）①

为了方便后文研究，在这部分里将通过股票分组得到的5×5投资组合月度平均超额收益的平均值列于下表1中。从下表1可以看出，在三个面板A、B、C的数据里，除个别列之外规模（Size）较小的分组的平均收益依次高于规模相对较大的分组的平均收益，而且三个面板各行数据的平均值也随着规模的增大逐渐变小，表明我国股市存在着明显的规模效应特征。从面板A各行的数据可以看出，第2行和第3行及规模最大的行的值越向右其值越大（除第2行和第3行的最右端，规模最大行的最左端），而且各列的平均值除最左边的值之外其值依次变大，也就是说B/M值越高月度收益的平均值越大，表明我国股市里存在B/M效应特征，但也表现出了翘尾现象。田利辉等[17]在他们的研究中也发现了这一现象。从面板B的各行可以看出，规模最小的行、第3小、第4小和规模最大的行都存在较为明显的由四个值构成的渐变特征，但其中前两行和后两行表现出来的规律截然不同，前两行表明盈利能力越弱的上市公司的组合越可能获得更高的平均收益，而后两行则表明盈利能力越强的上市公司的组合越可能获得更高的平均收益，这表明在盈利能力表现出来的特征上，规模大的分组表现出来的特征与美国股市表现出来的特征较为近似，但规模小组却相反。不过由各列的均值表现出的特征表明我国股市的主要特征是，盈利能力越强月度平均收益越低，这与美国股市表现出来的特征相反。从面板C各行可以看出，在规模最小的行、规模第4小的行和规模最大的行存在四个值构成的特征；但是，规模最小的行和规模最大的行呈现的渐变特征表明投资越激进的组合的月度平均收益值越小，而规模第4小的行表现的特征则相反；另外各列的平均值从左至右依次变小；因此面板C表明在我国股市里表现出的与投资相关的主要特征是投资越激进的上市公司组合越可能获得更低的平均收益，这与美国股市表现来的特征相同。由以上分析可以发现，我国股市中的平均收益也存在规模、B/M、盈利和投资相关的特征。

3 实证研究

3.1 Fama-Macbeth横截面回归分析

首先使用Fama-Macbeth两步法对全部样本进行回归检验，研究规模、账面市值比、盈利和投资四个因素在独立或联合时解释个股横截面收益差异的显著性。其次，为了进一步分析这四个因素在不同规模下的情况，本文将每年的样本均分成规模大组和规模小组，然后再分别对样本期内所有规模大的和小的组进行Fama-Macbeth两步法回归。由Fama-Macbeth横截面回归得到的主要研究结果列于下表2中（其中的t值为用Newey-West估计法计算异方差自相关稳健标准误然后得到的值②）。先分析单个因素独立起作用时的表现，从下表2全样本下列示的数据可以看出，规模因素、账面市值比因素、盈利因素和投资因素系数的值的绝对值依次变小，说明它们在解释个股横截面收益差异上的显著性依次减弱。而且只有账面市值比因素的系数为正值，也就是说，规模越大的股票的收益率越低，账面市值比越低股票的收益率越低，盈利能力越强股票收益率越低，投资越激进股票收益率也越低。这些再次证明了表1中表现出的主要效应特征。进一步比较由Fama-Macbeth两步法得到的规模大组和规模小组各因子系数的值，可以发现规模因素在两个组的显著性基本无差异，账面市值比因素在规模大组的显著性明显高于规模小组；而盈利因素和投资因素则表现相反，它们在规模大组的显著性明显低于规模小组。再者，在控制规模因素后，账面市值比因素的t值在规模大的样本里仍然大于1，而盈利和投资因素的t值的绝对值则在规模小的样本里大于1。在研究对象为全部样本和规模大的样本时，在控制其它三个因素后，账面市值比因素、盈利因素和投资因素的t值绝对值都小于1；但在研究对象为规模小的样本时，在控制其它三个因素后，盈利因素和投资因素的t值绝对值仍然分别保持在了1.48和1.24。分析由三个样本得到的结果可以发现，规模因素t值的绝对值在所有情况下都大于1.972(p=0.05)；但其它三个因素t值的绝对值既不存在大于1.972的情况，也不存在大于1.653(p=0.10)的情况。因此可以说，在解释个股的横截面收益差异上，规模因素具有较高的显著性，而账面市值比(B/M)因素、盈利因素和投资因素均显著性不高。

表2 Fama-Macbeth回归主要结果③

3.2 模拟因子进行时间序列回归分析

（1）因子的描述性特征和关系

表3 因子的描述性统计表现

表3描述了使用2×3组合的方法构建的各因子的主要统计量。我国股市市场超额收益()平均值为1.08%，表现为正的市场溢价，但在5%显著性水平(t=1.972)下不显著异于零,而在10%显著性水平(t=1.653)下显著异于零；规模因子()的值为0.91%，且在5%显著性水平下显著异于零；从账面市值比因子()和盈利因子()平均值的t统计量可以看出，它们都不显著异于零，而且盈利因子为负值；投资因子()的值为0.24%，但不显著异于零。

Fama和French[11]指出，在美国股市里因子的引入不会改变模型的均值方差有效性，在他们构建的五因子模型里是“冗余因子(redundant factor)”。这里，我们使用他们的方法检验本文构建的因子是否存在“冗余因子”。下表4里列出的是依次用其余四个因子对第五个因子回归得到截距项及其t检验统计量。

表4 用其余四个因子对第五个因子回归得到的截距项的统计特征

从表4可以看出，回归得到的后四个截距项都在5%的显著性水平下显著异于零，而第一个截距项则在10%的显著性水平下显著异于零，表明在我国股市里五个因子都不是“冗余因子”。

(2) 因子模型回归分析的主要结果

使用两个因子模型(3)和(4)分别对按规模-账面市值比(Size-B/M)、规模-盈利(Size-OP)和规模-投资(Size-Inv)分组得到的5×5投资组合的月度平均收益进行回归分析，得到的主要回归结果列于表5-7，由于研究使用的是18年216个月度的样本数据，查看t检验临界值表可以看出，p=0.05时t值约为1.972，而p=0.10时t值约为1.653，直接使用这两个临界值可以直观上判断回归得到的截距项和因子系数的显著性。另外，为了检验各定价模型在回归时是否表现出多重共线性，

本文使用方差膨胀因子来进行判断。通过进一步使用由两个定价模型回归投资组合平均收益得到的结果计算方差膨胀因子，发现所有变量的VIF值都小于5。因此，可以说本文研究的两个定价模型都不存在明显的多重共线性问题。

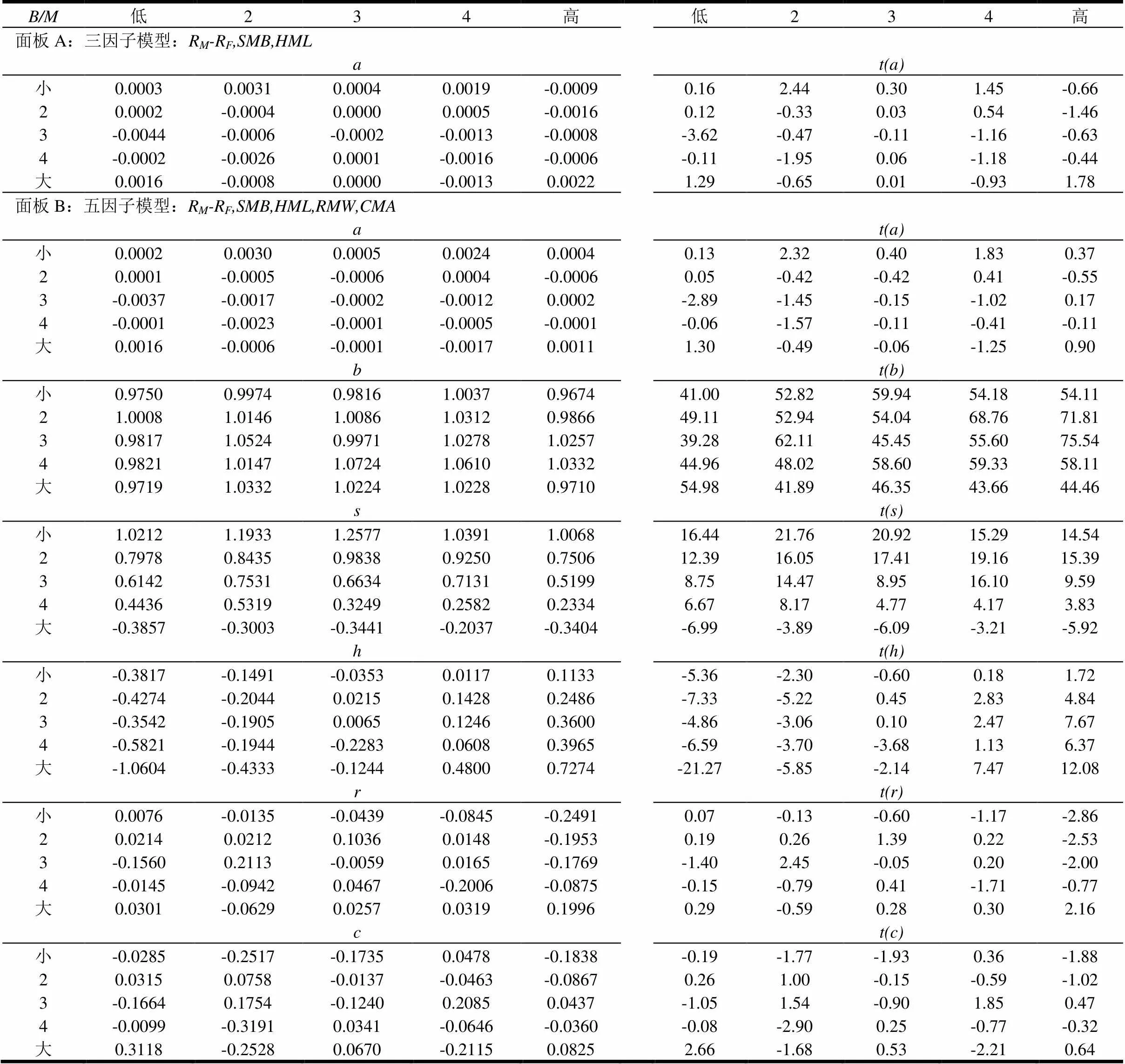
表5 Size-B/M分组平均收益的主要回归结果④

从上表5可以看出，在25个Size-B/M分组组合回归得到的截距项中，三因子模型和五因子模型在5%显著性水平下各有2个显著异于零，而在10%显著性水平下三因子模型和五因子模型分别有4个和3个t统计量显著异于零，说明在解释按规模-账面市值比（Size-B/M）分组的平均收益上，五因子模型比三因子模型更有优势；市场因子系数在0.9674-1.0724之间且t统计量表明其显著异于零；规模因子系数差异较大，规模最小的组合的因子系数都大于1，随着规模增大，因子系数逐渐变小，至规模最大的分组因子系数变为负值；账面市值比因子系数随着账面市值比的变大，其值也逐渐变大（只有规模为4且账面市值比为2，3表现出了异常），而且这25个系数中在5%显著性水平下只有6个不显著异于零，在10%显著性水平上只有5个不显著异于零，表明账面市值比因子对模型有显著贡献。但是，此时盈利因子的系数和投资因子的系数在5%显著性水平下分别有5个和3个显著异于零，在10%显著性水平下分别有6个和8个显著异于零。

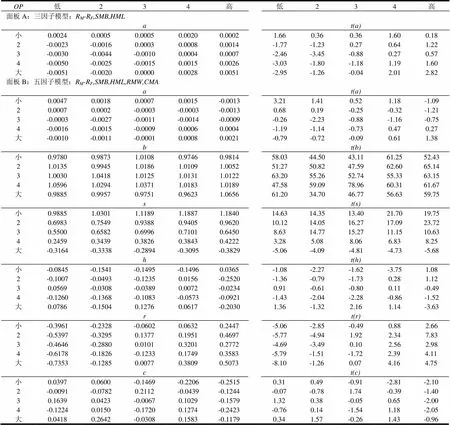
表6 Size-OP分组平均收益的主要回归结果

从表6可以看出，在25个Size-OP分组组合回归得到的截距项中，三因子模型在5%和10%显著性水平下分别有6个和9个显著异于零，而五因子模型在两个显著性水平下都只有2个显著异于零，说明在解释按规模-盈利（Size-OP）分组的平均收益上，五因子模型比三因子模型更有优势；市场因子和规模因子的系数也都如表5里那样全部显著异于零；盈利越高的分组的盈利因子系数越大（只有规模为3且盈利为4、最高的两个值表现出了异常），而且得到的25个系数中在5%显著性水平下只有8个不显著异于零，在10%显著性水平下只有6个不显著异于零，说明盈利因子的引入有助于解释按规模-盈利分组的平均收益。但此时，账面市值比因子系数和投资因子系数在5%显著性水平下分别有6个和4个显著异于零，在10%显著性水平下分别有7个和5个显著异于零。

从表7可以看出，在25个Size-Inv分组组合回归得到的截距项中，三因子模型和五因子模型在5%和10%的显著性水平下都分别有4个和5个显著异于零，说明在解释按规模-投资（Size-Inv）分组的平均收益上，五因子模型与三因子模型相比两者表现较为接近；市场因子和规模因子的系数也都如表5和表6中那样显著异于零；除个别值例外以外投资越激进（Inv值越高）的分组的投资因子系数越小，而且得到的25个系数中在5%显著性水平下有13个不显著异于零，在10%的显著性水平下有9个不显著异于零，说明投资因子的引入有助于解释按规模-投资分组的平均收益。但此时，账面市值比因子系数和盈利因子系数在5%显著性水平下分别有8个和6个显著异于零，在10%显著性水平下各有9个显著异于零。

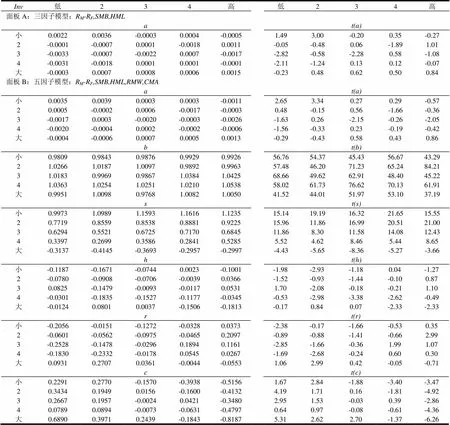
表7 Size-Inv分组平均收益的主要回归结果

（3）GRS检验和各模型的总体评价

为了对两个因子模型在拟合按规模-账面市值比（Size-B/M）、规模-盈利（Size-OP）和规模-投资（Size-Inv）分组的5×5投资组合的月度平均收益的表现进行总体评价，本文参照Fama和French[11]的方法分别使用Gibbons等[23]提出的GRS检验对各模型拟合不同投资组合平均收益的效果进行检验，得到的p值列于下表8；同时计算用两因子模型回归得到的截距项绝对值的均值（）及其与的比值（），这里的为表1各面板相应分组中第个值与其全部值的均值之差（如研究Size-B/M分组时，则表示面板A中的第个值与面板A中全部值均值的差）；表示调整的拟合优度的均值。计算得到各指标同样列于下表8中。在这里，GRS检验以回归25个组合月度收益时的所有截距项是否同时为零为原假设，在研究时一般使用p=0.05为分界线，如果得到的p值大于0.05则接受原假设，表明模型能解释所检验组合的平均收益特征，否则不能解释。再者，p值越大效果会越好。对于和两个指标，它们都表示平均收益中不能被模型解释的部分，值越小模型解释平均收益的效果越好。表示模型的对序列变异的拟合效果，其值越大拟合效果越好。

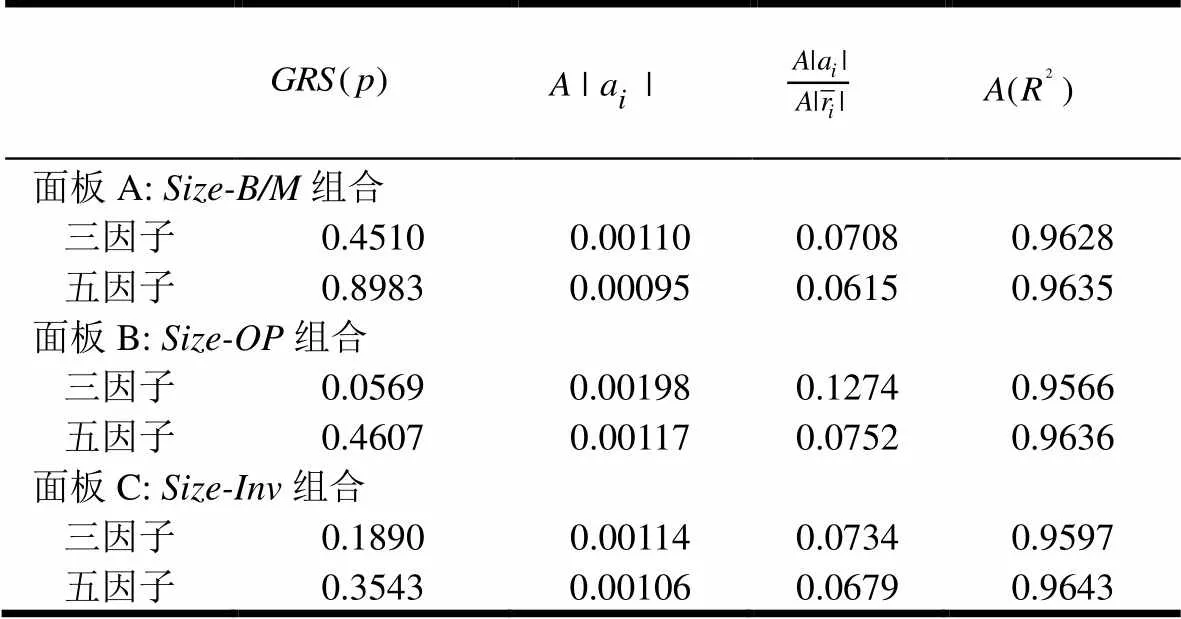
表8 2×3因子构造法下各模型的总体评价

从表8可以看出，三因子模型和五因子模型的GRS检验p值都大于0.05，所以可以说它们都能够有效地拟合我国股市的平均收益特征；比较五因子模型和三因子模型的四个评价指标可以发现，GRS检验的p值和在拟合三组投资组合序列时前者得到的值都大于后者，而且和两个指标的值都小于后者。因此可以说，在拟合我国股市表现出来的特征上五因子模型优于三因子模型。

（4）因子构造法不同时研究结果的稳健性

为了测度前文所得结论的稳健性，本文进一步按Fama和French[11]曾使用的另外两种因子构建方法（即2×2因子构造法和2×2×2×2因子构造法）获得各因子序列，然后分别进行GRS检验和回归，并计算回归截距项绝对值的均值、调整拟合优度的均值等，主要相关结果列于下表9中。分析下表9可以发现，对于两个因子构造法和三个面板数据，五因子模型GRS检验的p值都大于三因子模型的p值，由五因子模型得到的和的值都小于由三因子模型得到的值，而由五因子模型得到的又都大于由三因子模型得到的相应值。这些结果与前文使用2×3因子构造法得到的结论相一致，因此结论具有稳健性。也就是说，使用三种因子构造法进行的研究都表明，在拟合我国股市表现出来的特征上五因子资产定价模型优于三因子资产定价模型。

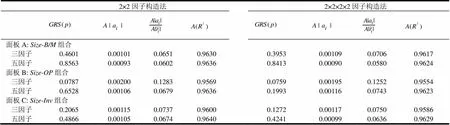
表9 其它两种因子构造法下各模型的总体评价

4 结束语

本文选取1997年以来我国股市的数据为样本，综合运用Fama-Macbeth回归法和构建投资组合模拟因子法，研究了上市公司的规模、账面市值比(B/M)、盈利和投资等因素在资产定价中的作用。得出以下结论：

（1）在解释个股横截面收益差异上，规模因素具有较高的显著性，而B/M、盈利和投资三个因素并不具有较高的显著性，且它们的显著性依次降低。再者，B/M因素的影响在规模较大的上市公司分组里更显著，盈利和投资因素则在规模较小的上市公司分组里更显著。

（2）我国股市的平均收益不仅呈现出与规模、B/M相关的效应特征，而且也呈现出与盈利、投资相关的效应特征。其中规模效应表现为规模越大的公司的股票收益越低；B/M效应特征表现为B/M越高的公司的股票收益越高，但存在翘尾现象；盈利效应的主要特征表现为盈利能力越强的公司的股票收益越低，但规模较大的公司则表现为盈利能力越强的公司的股票收益越高；投资效应的主要特征表现为投资越保守的公司的股票收益越高。

（3）与美国股市不同，我国股市里的账面市值比因子不是“冗余因子”，不能完全由市场因子、规模因子、盈利因子和投资因子解释。

（4）在解释我国股市月度平均收益存在的与规模、B/M、盈利和投资相关的效应特征上，五因子资产定价模型和三因子资产定价模型都可以较好对这些特征进行解释。但是，在表现上五因子资产定价模型要优于三因子资产定价模型。

[1] Sharpe W. Capital asset prices: a theory of market equilibrium under conditions of risk [J]. Journal of Finance, 1964, 19: 425-442.

[2] Black F, Jensen MC, Scholes M. The capital asset pricing model: some empirical tests[A]. Jensen MC. Studies in the theory of capital markets[C]. Praeger Publishers Inc., 1972.

[3] Fama EF, Macbeth JD. Risk, Return and Equilibrium: Empirical Tests [J]. Journal of Political Economy, 1973, 81(3):607-36.

[4] Banz RW. The relationship between return and market value of common stocks [J] . Journal of Financial Economics, 1981, 9(1): 3-18.

[5] Stattman D. Book values and stock returns[J]. The Chicago MBA: A Journal of Selected Papers,1980, 4: 25-45.

[6] Fama EF, French KR. Common risk factors in the returns on stocks and bonds[J]. Journal of Financial Economics, 1993, 33: 3-56.

[7] Carhart MM. On persistence in mutual fund performance [J]. Journal of Finance, 1997, 52(1): 57-82.

[8] Novy-Marx R. The other side of value: The gross profitability premium[J]. Journal of Financial Economics, 2013, 108: 1-28.

[9] Aharoni G, Grundy B, Zeng Q. Stock returns and the Miller Modigliani valuation formula: revisiting the Fama French analysis [J]. Journal of Financial Economics, 2013, 110: 347-357.

[10] Hou K, Xue C, Zhang L. Digesting anomalies: An investment approach [J]. The Review of Financial Studies, 2015, 28(3): 650-705.

[11] Fama EF, French KR. A five-factor asset pricing model[J]. Journal of Financial Economics, 2015, 116: 1-22.

[12] Eoghan N, Michael D. Profitability and Investment Factors for UK Asset Pricing Models [J]. Economics Letters, 2014,125: 364-366.

[13] 范龙振,王海涛.上海股票市场股票收益率因素研究[J].管理科学学报,2003,6(1):60-67.

[14] 杨炘,陈展辉.中国股市三因子资产定价模型实证研究[J].数量经济技术经济研究,2003,12: 137-141.

[15] 邓长荣,马永开.三因素模型在中国证券市场的实证研究[J].管理学报,2005,5: 591-596.

[16] 刘维奇,牛晋霞和张信东.股权分置改革与资本市场效率—基于三因子模型的实证检验[J].会计研究,2010,3: 65-72.

[17] 田利辉,王冠英和张伟.三因素模型定价：中国与美国有何不同？[J].国际金融研究,2014,7: 37-45.

[18] 李倩,梅婷.三因素模型方法探析及适用性再检验：基于上证A股的经验数据[J].管理世界,2015,4: 184-185.

[19] 潘莉,徐建国.A股市场的风险与特征因子[J].金融研究,2011,10:140-154.

[20] 田利辉,王冠英.我国股票定价五因素模型：交易量如何影响股票收益率？[J].南开经济研究,2014,2:54-75.

[21] 王茵田,朱英姿.中国股票市场风险溢价研究[J].金融研究,2011,7:152-166.

[22] Miller M, Modigliani F. Dividend policy, growth, and the valuation of shares [J].Journal of Business,1961,34: 411-433.

[23] Gibbons M, Ross S, Shanken J. A test of the efficiency of a given portfolio [J]. Econometrica, 1989, 57: 1121-1152.

① 为了更方便地发现数据间的规律性特征，不仅计算了各行和各列的平均值，而且对其中由四(或五)个行数据表现出渐变特征的数据进行了加粗。

② 文其余部分的回归分析中涉及到的t统计量也都是使用这一方法进行调整得到的相应值。

③ 表2中括号内的值为相应系数对应的t统计量，行中出现并列几个系数时表示使用Fama-MacBeth回归对相应因素进行联合检验。为了简便，对多个因素联合的情况，这里只给出了规模因素分别与其它因素联合及四个因素联合时得到的检验结果。

④ 考虑到研究的需要，面板A只给出了三因子资产定价模型回归的截距项及其t统计量。面板B依次给出了五因子资产定价模型的截距项、各因子的系数及它们的t统计量。表6和表7相同。

Corporate Profitability, Investment and Asset Pricing:An Empirical Research about Chinese Stock Market

GAO Chun-ting，ZHOU Xiao-hua

(School of Economics and Business Administration, Chongqing University, Chongqing 400030, China)

Fama and French (1993) proposed a three-factor asset pricing model based on market factor, size factor and B/M factor. This model had become a widely used asset pricing model in empirical financial researches. Recently, Fama and French (2015) added profitability and investment factors to their three-factor model and obtained a five-factor asset pricing model. With monthly data in U.S. stock market, they found that five-factor model performed better than three-factor model on capturing the patterns in average returns related to size, B/M, profitability and investment. Following their idea, with the ratio of operating profit to book value as profitability factor and the growth rate of total assets as investment factor, we conduct a research on the performance of five-factor asset pricing model about Chinese stock market.

The research focuses on the period from July 1997 to June 2015. We first use Fama and Macbeth regression to study the power of size, B/M, profitability, investment factor on explaining the cross-section returns. In this part, we also separate the sample of every year by big stocks and small stocks in order to do further analysis. We find that the explaining power of the four factors decrease in sequence for the whole sample. The B/M factor plays a more significant role in big stocks samples than that in small stocks samples. However, profitability and investment factors play more significant role in small stocks samples. Moreover, there is no difference between the big stocks sample and the small stocks sample for the significance of size factor coefficients.

By 5×5 portfolios, we find that there are patterns in average returns related to size, B/M, profitability and investment in Chinese stock market too. However, the patterns are different from that in US stock market. For the patterns related to B/M, higher B/M portfolio shows higher average returns except for the highest B/M portfolio. For the patterns related to profitability, the main pattern is that more robust profitability portfolio has lower average returns, which is very different from that in U.S. stock market. Moreover, pattern changes in different size. For the smallest to the third smaller size portfolios, the patterns are the same as the main pattern. However, for the other two bigger size portfolios, the pattern with the robust profitability portfolio has higher average returns, which is the same as that in U.S. stock market. The pattern related to investment is very similar to that in U.S. stock market. That is, more conservative investment portfolio has higher average returns. But there is also a special case in the second bigger portfolio.

With the three-factor model of Fama and French(1993) as a reference, we further construct five-factor asset pricing model following the idea of Fama and French (2015) and conduct an empirical research with data from Chinese stock market. Our regression and GRS tests show that the five-factor asset pricing model can well capture these patterns and its performance is better than that of the three-factor model.

asset pricing; five-factor model; profitability; investment；Fama-Macbeth regression

中文编辑：杜 健；英文编辑：Charlie C. Chen

F830

A

1004-6062(2016)04-0025-09

10.13587/j.cnki.jieem.2016.04.004

2015-11-30

2016-03-10

国家社会科学基金资助项目（14ZDB148）

高春亭(1982—)，男，河北衡水人；重庆大学经济与工商管理学院博士研究生，研究方向：证券投资与资产定价。